便携式反坦克导弹弹道成型制导律设计

便携式反坦克导弹弹道成型制导律设计

侯博1,2,宋建梅1,2,张春妍1,2,黄岚1,2

(1.北京理工大学 宇航学院,北京 100081;2.飞行器动力学与控制教育部重点实验室,北京 100081)

摘要:针对飞行速度快速时变的便携式反坦克导弹制导控制问题,应用最优控制原理,提出了一种考虑导弹速度快速变化的改进弹道成型制导律。采用超前滞后环节进行时变过载自动驾驶仪设计;基于最优控制理论推导了广义弹道成型制导律和扩展弹道成型制导律,针对便携式导弹速度快速时变的特性,设计了包含时变速度信息的弹道成型制导律,并结合工程实际讨论了参数选择方法;最后进行了仿真对比和验证。仿真结果表明,该文提出的包含时变速度信息的弹道成型制导律能够满足武器系统的近距击顶作战需求,同时能够满足导弹系统的着角、攻角、框架角、过载等约束。

关键词:便携式反坦克导弹;着角;广义弹道成型制导律;最优控制

中图分类号:TJ765.3文献标识码:A

收稿日期:2014-04-23

基金项目:燃烧与爆炸技术重点试验室

作者简介:王燕(1986- ),女,讲师,研究方向为发射装药发射安全性。E-mail:wangyanqianhuang@163.com。

Trajectory Shaping Guidance Law Design for Portable Anti-tank Missile

HOU Bo1,2,SONG Jian-mei1,2,ZHANG Chun-yan1,2,HUANG Lan1,2

(1.School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China;2.Key Laboratory of Dynamics and Control Flight Vehicle,Ministry of Education,Beijing 100081,China)

Abstract:Aiming at the guidance and control problem of the portable anti-tank missile with fast-varying velocity,an improved trajectory shaping guidance law(TSG)taking into account varying velocity was proposed based on the optimal control theory.The lead-lag controller was designed for the acceleration autopilot of the anti-tank missile.According to the optimal control theory,the generalized TSG and extended TSG were deduced.The improved TSG including the information of the fast varying velocity was designed,and the rule of parameter selection for the improved TSG was discussed.Simulation results show that the improved TSG proposed in this paper can make the missile attack the target from the top in short rang and satisfy the system requirements,as well as the impact angle,the attack angle,frame angle and acceleration constraints.

Key words:portable anti-tank missile;impact angle;generalized trajectory shaping guidance law;optimal control

便携式反坦克导弹因其轻便灵活、操作简单、可单兵或2-3人兵组携带、命中率高、威力大等优点,已经成为当今战场尤其是快速部署部队的重要武器。它以较大着角命中近距离处的坦克目标,实现近距击顶,增大毁伤效果。该导弹采用软发射技术,初始速度低,导弹发射后速度快速增加。如何在速度快速变化和导弹过载、攻角、导引头框架角等多重约束条件下进行便携式反坦克导弹近距击顶弹道设计,这是本文研究的重点。

基于最优控制原理的弹道成型制导律,将控制能量最小作为最优控制问题的性能指标来设计导引律,通过在性能函数中加入权重函数,对制导过程中的控制能量进行合理分配,得到满足不同性能需求的弹道成型制导律[1-5]。目前权重函数大致可以分为三大类:常数1、剩余飞行时间的n次方、其他形式等。

文献[6]最早采用最优控制原理设计同时满足脱靶量和着角约束的制导律。文献[1]对文献[6]中的方法进行了进一步研究,将其称为弹道成型制导律(trajectory shaping guidance,TSG),并与比例导引律进行了仿真对比。文献[2]分别在有无动力学滞后2种情况下推导了基于状态反馈形式的最优制导律,研究了不同剩余时间估算方法(time-to-go)对弹道的影响。文献[7]通过求解引入偏置项的线性化比例导引方程,设计了偏置比例导引律,偏置项反映了当前弹道倾角与期望着角的误差信息。上述文献都是针对权重函数为常数1的传统弹道成型制导律进行的研究。传统弹道成型制导律本质上是一种将控制能量在整个制导过程中平均分配的导引方案,不容易满足导弹系统总体对攻角、过载等的约束条件,另外上述文献在制导律推导过程中都假设导弹速度为常数。

文献[3]引入剩余飞行时间(time-to-go)的n次方作为权重函数,实现了对传统弹道成型制导律的改进。文献[8]对这一制导律进行了进一步研究,并将其称为扩展弹道成型制导律(extend trajectory shaping guidance,ETSG)。文献[8]和文献[9]通过求解线性二次型最优控制问题得到扩展弹道成型制导律,针对无动力学滞后的制导系统,利用Schwartz不等式,求解得到了在初始位置误差、方向误差、目标常值机动及终端着角约束情况下的加速度指令解析解。文献[10]针对无动力学滞后的ETSG系统,采用伴随方法详细讨论了着角约束条件、初始方向角误差等对脱靶量和末端着角误差的影响,并进行了仿真验证。文献[11]通过研究采用扩展弹道成型制导律的导弹的需用过载以及位置和角度脱靶量的特性,讨论了权重函数中导弹剩余飞行时间tgo的阶次对制导律的影响。上述文献均采用剩余飞行时间的n次方倒数作为权重函数,这一方法可以在初始段给导弹分配较多的控制能量,减小末段的过载需求。上述文献在制导律设计中都认为导弹速度不变,因而不适用于速度快速剧烈变化的便携式反坦克导弹;此外,这些文献也没有考虑攻角、框架角和过载等约束条件。

文献[12]利用Schwartz不等式,推导了包含着角约束的一般权重函数的弹道成型制导律的广义表达式,实现了对弹道成型制导律的进一步拓展。在此基础上,文献[4]通过引入分段线性的权重函数设计了针对远距离目标的反坦克导弹制导律,通过适当的参数选择,能够实现高平飞弹道。文献[5]通过引入高斯函数作为权重函数,设计了一种新的弹道成型制导律,适当地选择设计参数,能够分配飞行过程中的过载,防止过载饱和,减小初始段的过载需求。这些文献虽然对弹道成型制导律进行了进一步的拓展研究,但是在制导律设计和仿真研究的过程中,都是假设导弹速度不变,且假设导弹为可控质点,没有进行导弹自动驾驶仪设计。

本文主要针对飞行速度时变的便携式反坦克导弹进行了弹体动力学参数时变情况下的自动驾驶仪设计,在此基础上进行了带着角约束的弹道成型制导律设计,通过在权重函数系数中引入时变速度信息,使导弹达到了近距击顶的目的,同时满足了导弹系统过载、攻角、导引头框架角等约束条件,进一步结合工程实际讨论了参数选择方法,并通过仿真验证了本文设计的制导律的合理性与可行性。

1动力学参数时变的便携式反坦克导弹自动驾驶仪设计

针对便携式反坦克导弹非线性动力学模型,基于小扰动假设进行导弹纵向动力学方程线性化[13],得到弹体俯仰通道传递函数:

(1)

式中:KM为导弹传递系数,NM为导弹的时间常数,ξM为导弹的相对阻尼系数,N1为导弹气动力时间常数。

根据导弹的飞行速度范围,选取不同速度下的弹体动力学系统特征点,在每个特征点设计过载自动驾驶仪,其中的控制器采用超前滞后校正环节以满足系统相位裕度和幅值裕量的要求,然后通过线性插值得到整个飞行过程的控制器。限于篇幅,自动驾驶仪详细设计过程及设计结果略。

2基于最优控制理论的广义弹道成型制导律推导

2.1　 最优制导问题描述

考虑图1所示坐标系,OXIYI为惯性系,T为目标,M为导弹。定义一个参考坐标系TXRYR,其原点在T,由惯性系OXIYI经过顺时针旋转θf得到,其中θf为期望的着角。图中,aM为垂直于导弹速度方向的加速度,vM为导弹速度,θ为弹道倾角,q为弹目视线角。则TXRYR坐标系下的弹道倾角和弹目视线角表达式为

(2)

图1　弹目相对运动示意图

在参考坐标系TXRYR下有:

(3)

应用小角度线性化,式(3)可表示为

(4)

式中:y,v分别为垂直于XR轴的弹目距离和导弹速度。另外,有:

(5)

式中:R为弹目相对距离在XR方向上的投影;tgo=tf-t,为导弹剩余飞行时间;tf为导弹总飞行时间,则

(6)

将式(4)表示成状态空间形式:

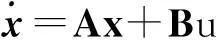
(7)

式中:

x=(yv)T, u=aM,A

(8)

导弹命中目标时期望脱靶量为0,期望着角为θf,则在参考坐标系TXRYR下的期望终端为

(9)

考虑求解最优控制u使如下的性能函数J取得最小值:

(10)

其中加权矩阵:

(11)

式中:s1,s2为常数;W(t)为权重函数,通过不同的权重函数选择,可以对控制信号施加约束,进而对飞行过程中的过载进行分配,得到满足不同性能要求的制导律。下面通过求解上述线性二次型最优控制问题进行广义弹道成型制导律(TSG)的推导。

2.2　广义弹道成型制导律

上述问题属于自由终端的有限时间状态调节器问题,根据极小值原理,引入协状态矢量λ(t),构造哈密尔顿函数:

λT(Ax+Bu)

(12)

可以求得最优解为

u*=-W-1BTφ(tf,t)Sf[x(tf)-xf]

(13)

式中:φ(tf,t)为从t时刻到tf时刻的状态转移矩阵,其表达式为

(14)

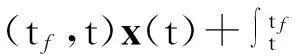
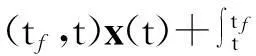
Sf[x(tf)-xf]

(15)

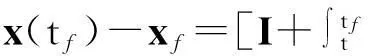
[φ(tf,t)x(t)-xf]

(16)

则有

(17)

式中:

(18)

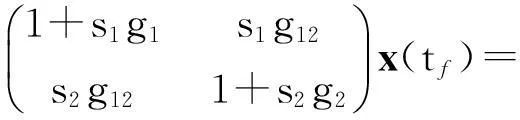
(19)

由方程(19)可以解得:

(20)

由式(13)可以得到:

u*=-W-1(t)[y(tf)s1(tf-t)+s2v(tf)]

(21)

由于

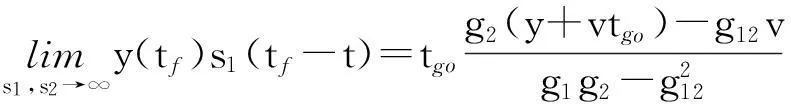
(22)

(23)

将式(22)、式(23)代入式(21)可以得到:

(24)

式中:

(25)

求得的最优控制u*即为弹体的过载输入信号aM,进一步可以将式(25)转化为比例导引加偏置项的形式。

将

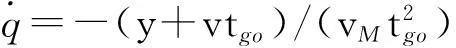
y=vMtgo(θf-q),

v=vM(θ-θf),

代入式(24),并令N=k1/2,得到:

(26)

上述推导过程采用了小角度假设,虽然当期望着角θf较大时,小角度假设不再成立,但TSG方法的鲁棒性较强,即使着角接近90°,TSG仍能保证导弹以一定的位置和角度精度攻击目标[1,2,7],是工程可用的。

2.3　2种典型的弹道成型制导律

将W(t)=1代入式(18)、式(22)、式(23)和式(25),可以得到传统的弹道成型制导律:

(27)

转化为比例导引加偏置的形式:

(28)

传统的弹道成型方法将权重函数选为常数1,控制能量在整个导引过程中平均分配。

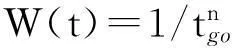
(29)

该扩展弹道成型制导律能够在初始段利用较大过载实现机动,而在接近终端位置时让需用过载较小甚至接近0。n的阶次越高,初始段弹道需用过载越大,弹道越弯曲;而末端需用过载越小,弹道越平直。当n>0时,命中点需用过载为0,并且n取值越大,终端需用过载趋向于0的趋势越平滑。传统的弹道成型制导律和扩展弹道成型制导律都是在假设导弹速度为恒速情况下推导得到的。

3时变飞行速度下的弹道成型制导律设计

针对便携式反坦克导弹速度快速变化的特征,本文将式(29)中的n设计为

(30)

式中:C1,C2是待定参数;tq为切换时间;vM为导弹速度。则本文提出的包含时变速度信息的弹道成型制导律为

(31)

由于导弹发射后导弹速度vM快速增加,所以,ttq时,n逐渐减小。这样设计的目的是,在初始段过载指令可以随着速度的增加而增加,达到充分利用可用过载进行爬高的目的。随着速度的增大,当t>tq以后,通过式(30)的第2式可以减小过载指令,平衡由于速度增大而导致的过载过大的问题。

为了保证制导指令在导引过程中不发生突变,要求n的值不要发生突变,因此在tq处需要保证:

vM(tq)/C1=C2/vM(tq)

(32)

加入了这样的约束以后,只需要确定tq,C1,C2中的任意2个参数,另一个参数就会随之确定。

本文通过讨论C1,C2,tq取值对弹道的影响来研究参数的选择规律。首先在满足过载和导引头框架角约束的情况下,C1的取值应尽量小,使得n的值尽量大以达到快速爬升的目的。在C1确定的情况下,为了保证式(32)成立,tq的取值越大,C2的取值也应该越大,tq和C2的取值越大,弹道爬升的高度越高,末段弹道会更加平直,过载也更小。tq为n值从增大趋势转变为减小趋势的时刻,因此,tq取值过大会导致无法及时减小n值而导致过载过大。但如果tq取值过小,更大的命中着角就无法实现。因此,应在综合考虑着角、脱靶量和过载以及攻角等约束的情况下合理选择tq的值。

下面进行便携式反坦克导弹的包含速度信息的弹道成型制导律设计。

4仿真实验

4.1　包含时变速度信息的弹道成型制导律有效性仿真

便携式反坦克导弹的初始俯仰角、弹道倾角为15°,过载限制在可用过载以内,舵偏角限制在10°以内,框架角限制在28°以内,攻角限制在18°以内,命中时刻的攻角限制在5°以内。

基于弹体气动参数,首先进行自动驾驶仪设计,然后基于包含时变速度信息的弹道成型制导律,分别对200m,300m,500m,1 000m等射程进行弹道参数的设计。再通过线性插值得到任意射程情况下的导引律参数,给出了250m,400m,700m的弹道设计参数。对便携式反坦克导弹射程分别为200m,250m,300m,400m,500m,700m,1 000m情况下的弹道进行仿真实验,命中目标时各变量仿真结果如表1所示,表中,L为射程,θf为命中目标时的弹道倾角,ϑf为命中目标时的俯仰角,αf为命中目标时的攻角,Dm(missdistance)为脱靶量,θd为期望弹道倾角。仿真得到的弹道曲线、攻角曲线、过载ny曲线以及n值的变化曲线如图2所示,图中X,Y分别为导弹在惯性坐标系中的位置。

从表1可以看出,包含时变速度信息的弹道成型制导律能够在满足各种约束的情况下实现大着角精确攻击。从图2(b)可以看出,在弹道末段弹体过载逐渐减小,过载曲线有收敛到0的趋势。从图2(a)也可以看出,末段的弹道曲线较为平直,说明包含时变速度信息的弹道成型制导律在弹道末段的过载需求较小,弹道较为平直,有利于提高命中精度。从图2(c)可以看出,最后攻击目标时刻攻角趋向于0,这有利于提高毁伤效果。另外通过图2可以发现,采用线性插值得到的250m,400m,700m的弹道参数能够在满足多重约束的情况下实现对目标的大着角攻击,充分体现了本文提出的包含时变速度信息的弹道成型制导律的有效性。

表1　不同射程下的仿真结果与弹道设计参数

图2　不同射程下的弹道成型制导律仿真曲线

4.2　包含时变速度信息的弹道成型制导律与传统弹道成型制导律的仿真对比

当射程为400m时,分别采用包含时变速度信息的弹道成型制导律(ETSGV)与传统弹道成型制导律(TSG)进行弹道仿真,得到的脱靶量分别为0.053m和0.088m,命中目标时的弹道倾角分别为-19.2°和-19°,攻角分别为-3.8°和-9.3°。弹道曲线、攻角曲线和过载曲线的比较如图3所示。从仿真结果可以看出,对于相同的期望着角,采用TSG制导律导弹命中目标时的攻角达到了-9.8°,已经超出了-5°以内的限制；而采用ETSGV制导律导弹命中目标时的攻角只有-3.8°。说明在本文限制条件下,相比于TSG制导律,采用ETSGV制导律导弹能够获得更大的着角,并且脱靶量也更小。

4.3　包含时变速度信息的弹道成型制导律与扩展弹道成型制导律的仿真对比

当射程为400m时,分别采用包含时变速度信息的弹道成型制导律(ETSGV)与扩展弹道成型制导律(ETSG)进行仿真对比研究,ETSG制导律中的n值选择为经过反复仿真实验得到的满足约束条件下能达到最大着角的值,为n=0.7。仿真得到ETSGV制导律和ETSG制导律的脱靶量分别为0.053m和0.070m,命中目标时的弹道倾角分别为-19.2°和-19.5°,命中目标时的攻角分别为-3.9°和-3.8°。2种制导律弹道曲线、攻角曲线的对比,如图4所示。

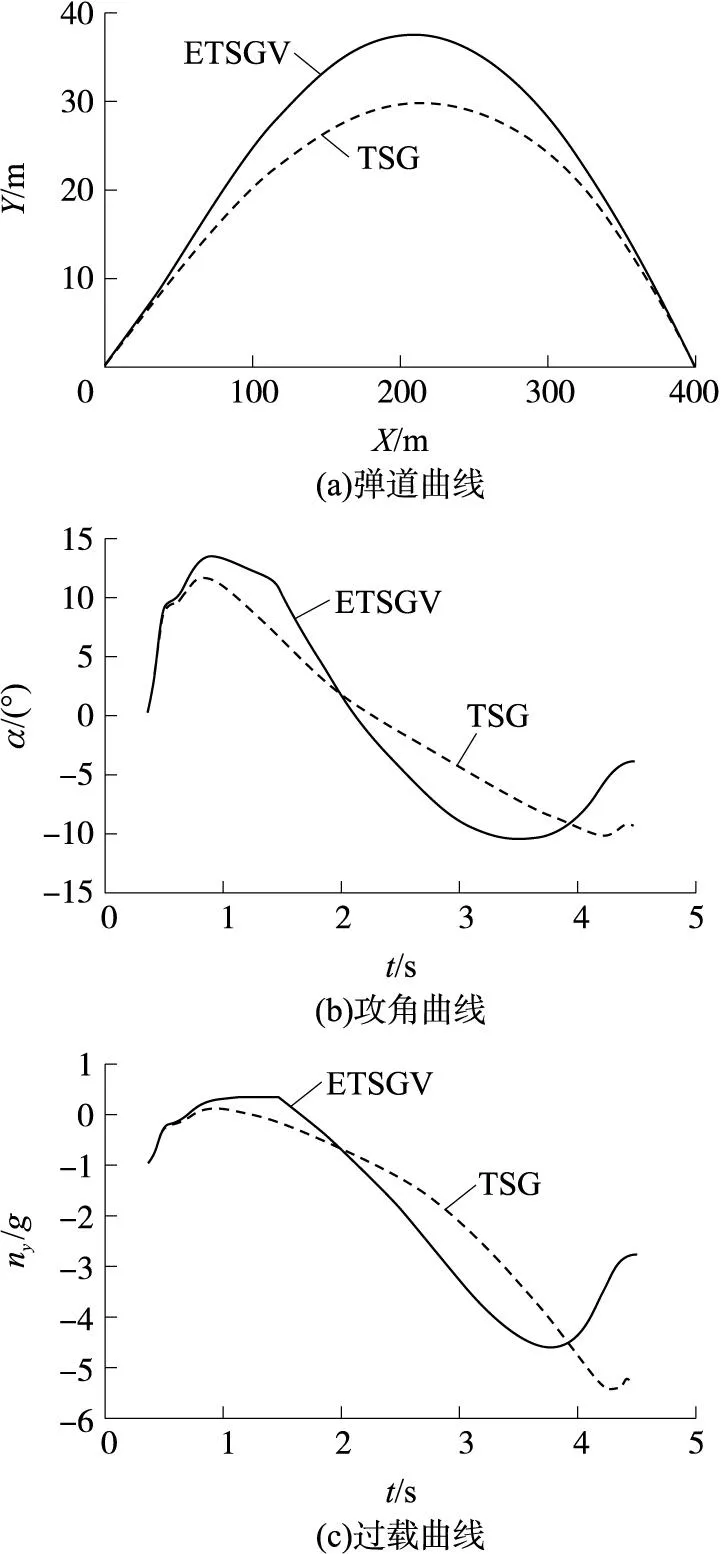
图3　ETSGV与TSG的仿真比较

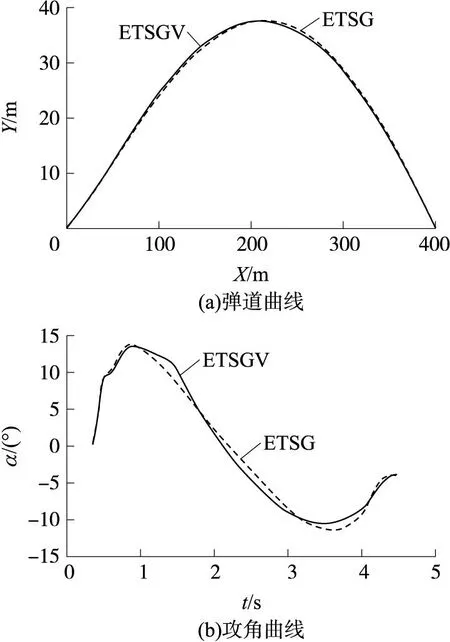
图4　ETSGV与ETSG的仿真比较

从仿真结果可以看出,ETSG制导律经过反复试凑得到的制导律设计参数与ETSGV按照插值选取的导引律设计参数,其飞行性能基本相同,导弹在导引下最终脱靶量和命中目标时的攻角基本相同,这进一步说明了本文设计方法的有效性。

5结论

本文针对便携式反坦克导弹近距离击顶的制导控制问题,应用最优控制理论,提出了一种考虑导弹速度快速变化的改进弹道成型制导律。针对便携式反坦克导弹时变的弹体特性,采用时变的超前滞后控制器,设计了不同飞行速度下的过载自动驾驶仪。结合扩展弹道成型制导律和导弹速度变化特性,通过引入包含速度信息的时变参数,提出了包含时变速度信息的弹道成型制导律,结合工程实际讨论了参数的选择方法,并通过仿真进行了验证。研究表明，本文提出的包含时变速度信息的弹道成型制导律能够针对弹体特性,更加合理地对飞行过程中的过载进行分配,充分利用导弹初始段的过载性能,降低了末段速度增大可能导致的过载饱和问题;并且由于减小了末段的过载需求,攻击目标时的弹道更加平直,脱靶量和攻角都更小,提高了制导精度和毁伤效果。同时,本文提出的弹道成型制导律能够满足导弹总体对过载、攻角、框架角等的多重约束。

参考文献

[1] ZARCHAN P.Tactical and strategic missile guidance.6th ed.Virginia,USA:AIAA Incorporate,2012:31-50,514-569.

[2] RYOO C K,CHO H,TAHK M J.Optimal guidance laws with terminal impact angle constraint.Journal of Guidance,Control,and Dynamics,2005,28(4):724-732.

[3] OHLMEYER E J,PHILIPS C A.Generalized vector explicit guidance.Journal of Guidance,Control,and Dynamics,2006,29(2):261-268.

[4] RYU M Y,LEE C H,TAHK M J.New trajectory shaping guidance laws for anti-tank guided missile.Journal of Aerospace Engineering(published online),2014,229(7):1 360-1 368.

[5] LEE J I,JEON I S,LEE C H.Command-shaping guidance law based on a Gaussian weighting function.IEEE Transactions on Aerospace and Electronic Systems,2013,50(1):772-777.

[6] CHERRY G.A general explicit,optimizing guidance law for rocket-propelled spacecraft//Proceeding of the AIAA/ION Astrodynamics Guidance and Control Conference.LOS Angeles:AIAA,1964:638-671.

[7] RYOO C K,TAHK M J,CHO H.Interception angle control guidance using proportional navigation with error feedback.Journal of Guidance,Control,and Dynamics,2013,36(5):1 556-1 561.

[8] RYOO C K,CHO H,TAHK M J.Time-to-go weighted optimal guidance with impact angle constraints.IEEE Transactions on Control Systems Technology,2006,14(3):483-492.

[9] 王辉,林德福,祁载康,等.扩展弹道成型末制导律特性分析与应用研究.兵工学报,2013,34(7):802-809.

WANG Hui,LIN De-fu,QI Zai-kang,et al.Analysis and application study on the extended trajectory shaping guidance law.Acta Armamentarii,2013,34(7):802-809.(in Chinese)

[10] WANG Hui,LIN De-fu,CHENG Zhen-xuan,et al.Optimal guidance of extended trajectory shaping.Chinese Journal of Aeronautics,2013,27(5):1 259-1 272.

[11] 刘大卫,夏群利,崔莹莹,等.具有终端位置和角度约束的广义弹道成型制导律.北京理工大学学报,2011,31(12):1 409-1 413.

LIU Da-wei,XIA Qun-li,CUI Ying-ying,et al.Generalized trajectory shaping guidance law with both impact position and angle constrains.Transactions of Beijing Institute of Technology,2011,31(12):1 409-1 413.(in Chinese)

[12] LEE C H,TAHK M J,LEE J I.Generalized formulation of weighted optimal guidance laws with impact angle constraint.IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1 317-1 322.

[13] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学.北京:北京理工大学出版社,2012:175-203.

QIAN Xin-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile flight aerodynamics.Beijing:Beijing Institute of Technology Press,2012:175-203.(in Chinese)