卵形弹丸垂直侵彻钢筋混凝土靶的工程解析模型

卵形弹丸垂直侵彻钢筋混凝土靶的工程解析模型

刘志林,孙巍巍,王晓鸣,李文彬

(南京理工大学 智能弹药技术国防重点实验室,南京 210094)

摘要:为了研究钢筋混凝土中钢筋对侵彻弹丸的阻力作用,通过对试验取出的钢筋混凝土试块的宏观和微观分析,在球形空腔膨胀模型的基础上,考虑弹丸直接与钢筋发生碰撞时钢筋对弹丸的阻力,建立了弹丸侵彻钢筋混凝土的工程解析模型。分析弹丸在钢筋交汇节点、钢筋网格中心点、单根钢筋的中点以及其他任意位置点与钢筋接触情况下钢筋对侵彻的影响。研究表明,钢筋混凝土中的钢筋不仅对混凝土的强度有影响,在弹丸撞击到钢筋时还对弹丸的侵彻能力有减小的作用。在网眼尺寸一定的条件下,随着体积配筋率的增大,钢筋对弹丸的阻力作用越明显,但在相同体积配筋率下,钢筋直径的影响小于钢筋网层间距的影响。

关键词:侵彻;钢筋;钢筋混凝土;空腔膨胀;电镜分析

中图分类号:O385文献标识码:A

Engineering Analytical Model of Ogive-nose Steel Projectiles Vertically Penetrating Reinforced Concrete Target

LIU Zhi-lin,SUN Wei-wei,WANG Xiao-ming,LI Wen-bin

(Ministerial Key Laboratory of ZNDY,NUST,Nanjing 210094,China)

Abstract:To study the resistance of steel in reinforced concrete while the projectile penetrating the target,the macroscopic and microscopic analysis of reinforced concrete block taken from the test was carried out.Based on the spherical cavity expansion model,the resistance of the projectile due to direct impact with reinforced was considered,and the projectile penetrating reinforced concrete engineering analytical model was established.The effect of steel bar on projectile was analyzed when the contact position located at the intersection node,the grid center point,the midpoint of a single reinforced and any other location points.The study shows that the steel bar in reinforced concrete not only affects the resistance of concrete but also deduces the penetration capability of projectile impacting steel bar.Under specific mesh size conditions,the resistance effect of reinforced on projectile becomes more obvious with the increase of rein forcement ratio,and the influence of bar diameter is less than that of the interlayer spacing of the steel mesh when reinforcement ratio is invariant.

Key words:penetration;steel bar;reinforced concrete;cavity expansion;electron microscopy analysis

钢筋混凝土不仅被广泛地用于民用领域,同时也是军事领域常用的防护建筑材料,以钢筋混凝土为目标靶的侵彻问题研究日益成为现在的研究热点和难点。国内外学者在弹丸侵彻混凝土的研究上做了大量的工作,总结了许多经验公式和理论模型,而对以钢筋混凝土为靶板的侵彻问题的研究,主要有实验、数值仿真、工程解析模型等方法。

文献[1-3]研究了钢筋在弹丸贯穿钢筋混凝土薄板中的影响,重点研究了钢筋对贯穿阻力的影响,而未对弹丸深侵彻钢筋混凝土厚靶问题进行研究。Luk V K[4]等应用空腔膨胀理论模型建立了卵形弹丸对钢筋混凝土靶侵彻深度的计算公式。其模型中只认为钢筋对混凝土径向裂纹扩展有阻碍作用,忽略了钢筋对弹丸的直接阻力作用。欧阳春[5]等在Luk V K等的基础上,应用球形空腔膨胀理论模型计算混凝土介质对弹丸的侵彻阻力,并且考虑钢筋对弹丸的阻力,模型中钢筋的破坏模式只考虑钢筋的弯曲破坏。穆朝民[6]等在用欧阳春等模型研究弹丸对钢筋混凝土中钢筋交汇处侵彻效应时发现实验与理论计算相差较大,理论计算侵彻深度值比实验测得值要小10%以上,最高误差达到27%。实验结果与理论计算的比较可以发现,欧阳春等模型中将钢筋对弹丸的影响考虑过大。目前弹丸侵彻钢筋混凝土的实验中弹丸着靶速度较低,数值仿真中钢筋对弹丸的阻力作用过大,从而弹体侵彻深度偏小。工程解析模型中,钢筋的处理方法是问题的关键,钢筋小梁的跨度、阻力和破坏准则直接影响弹体阻力的大小,现有模型中对相关参数定义差别较大且缺乏理论依据。

本文应用空腔膨胀理论模型计算混凝土对弹丸的侵彻阻力,并考虑钢筋对弹丸的直接阻力作用,根据侵彻实验中断裂钢筋的端口微观电镜分析判断钢筋断裂失效模式为弯曲加拉伸破坏,建立考虑钢筋直接对弹丸阻力的工程解析模型,分析不同配筋情况以及不同弹着点对侵彻的影响。

1工程解析模型

1.1　钢筋与弹丸的相互作用关系

弹丸在钢筋混凝土介质中的运动是一个非常复杂的问题,弹丸与钢筋的相互作用关系也是研究该问题的重点和难点。欧阳春和穆朝民等认为钢筋的响应分为弯曲段和断裂段。只有弹丸与钢筋接触时,钢筋才会对弹丸有阻力作用。当钢筋断裂后,此时钢筋失去轴向约束,钢筋与混凝土介质一起运动,钢筋对弹丸的阻力可以忽略。

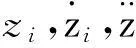
yi+1=yi-dzi+1cosφisinφi

(1)

zi+1=zi+dzi+1cosφicosφi

(2)

(3)

式(3)为弹丸ti到ti+1之间的位移,ti+1时刻弹丸位置信息的计算需要此时刻弹丸的轴向阻力,φi为ti时刻钢筋与弹丸接触点的法向与z轴的夹角。再根据牛顿第二定律求解侵彻深度。此刻弹丸受到的阻力包括钢筋对弹丸的阻力Fr和混凝土介质对弹丸的阻力Fc,则

(4)

式中:m为弹丸质量。

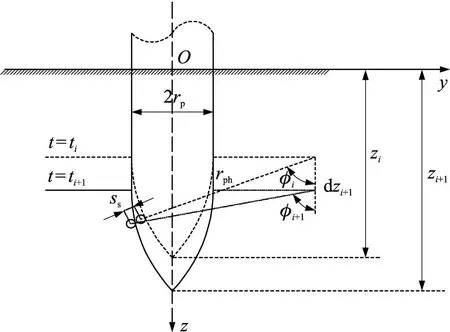
图1　弹丸与钢筋相互作用时的位置关系

1.2　钢筋对弹丸阻力的计算

弹丸撞击钢筋时,钢筋发生弯曲或断裂,此过程中钢筋与钢筋相互作用,其相互作用力会对弹丸侵彻有阻碍作用,为了计算其相互作用力,需对弹丸撞击后钢筋的响应进行研究。

为了明确钢筋在与弹丸的接触碰撞后的破坏失效模式,进行了弹丸侵彻钢筋混凝土的实验。实验采用直径为60 mm的尖卵形弹丸垂直侵彻配筋率为0.5%的钢筋混凝土。用圆筒形钻孔机沿弹道轴线切割钢筋混凝土靶板,切下带有钢筋网层的圆柱形混凝土试块,敲开试块取出钢筋网层,如图2(a)所示。弹丸侵彻靶板结束后,弹道附近的混凝土处于破碎区,强度很低,容易破碎,且切割作业的难度非常大,成功取出的带钢筋网层的混凝土试块并不多。观察取出的混凝土试块,可以清楚地判断弹孔侵彻后的孔洞与钢筋网层的相对位置。

图2(b)和图2(c)分别为在隧道中间段和末尾段取出的钢筋混凝土试块。由图2(b)可以观察到隧道孔洞以及孔洞周围的钢筋网,从图中可以看出,被撞击到的2根钢筋发生断裂,未被撞击到的另2根钢筋则完好无损。图2(c)中可以观察到,弹丸停留在钢筋混凝土中的状态与中间段的现象一样,弹丸接触的钢筋发生断裂,未接触到的钢筋则完好无损。

图2　隧道区附近取出的带钢筋网的混凝土试块

图3是图2(b)中的钢筋断裂情况示意图,图中显示了钢筋初始时刻状态(虚线表示)与撞击后的状态(实线表示)。从图中可以观察到弹丸撞击钢筋网格的弹着点,只有穿过隧道区的钢筋发生断裂,即弹丸撞击到的钢筋(图中虚线画出的2根钢筋)发生断裂,未撞击到的钢筋则保持初始状态。被弹丸撞击的2根钢筋发生塑性变形,钢筋受到混凝土介质和弹丸的挤压作用沿隧道区内壁弯曲。

从试块中取出钢筋网层中断裂的钢筋,钢筋发生明显的弯曲变形,断口处有明显的颈缩现象。用扫描电子显微镜(JSM-5610LV型扫描电子显微镜)对钢筋断口进行观测,发现断口分布着大量的韧窝,如图4所示,判断钢筋破坏属于典型的塑性断裂模式。根据对钢筋断口的分析,本文假定钢筋将在拉力和弯矩共同作用下发生薄膜拉伸和弯曲耦合断裂失效。

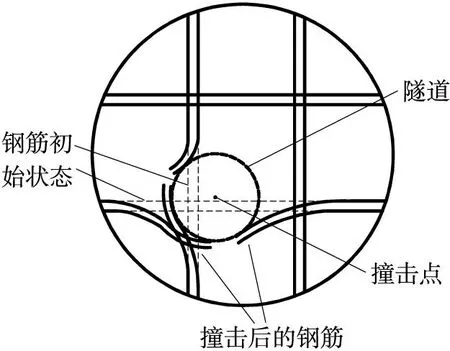
图3　初始钢筋状态与撞击后状态对比图

图4　钢筋断口电镜图

因此,本文将弹丸与钢筋的相互作用简化为一固支梁在阻尼介质中受到冲击载荷作用的动力学响应问题。钢筋的受力模型如图5所示。图中,Fλ为钢筋受到弹丸碰撞的作用力，sλ为钢筋与弹丸头部接触点的位移,L为小梁跨度。

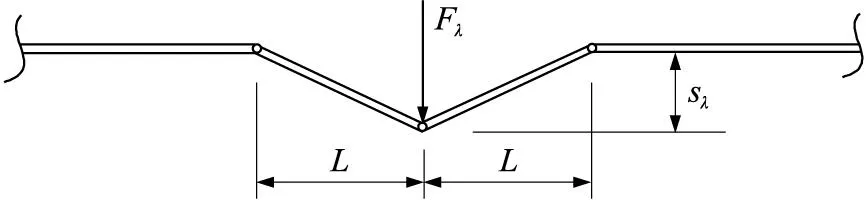
图5　钢筋的受力模型

随着静水压力的增加,混凝土的屈服包络线将变得越来越平缓直至达到极限,变成水平线,即混凝土介质不再抵抗切应变的继续增大。当压力值达到初始密实压力时,将出现流体密实区,混凝土介质可由弹性状态经内摩擦状态向理想流动状态(或接近流体动力状态)转变[7-9]。流动密实区内混凝土接近流体状态,这造成了钢筋和混凝土之间存在相对速度差,即钢筋与混凝土之间存在相对速度场。

本文根据动态空腔膨胀理论,假定钢筋受影响范围集中在流体密实区,其范围可近似用α1R(α1是与流体密实区外边缘应变相关的函数,R为空腔半径)表示[10],而其他区域假定为刚体,如图6所示。

α1=(1-e-3εα1/2 )-1/3

(5)

式中:εα1为混凝土流体区域外边缘应变。基于以上分析,可确定钢筋小梁的跨度为

(6)

图6　不同分区和钢筋的影响范围

流体区域外围假定为刚性(钢筋和混凝土共同工作),钢筋上与弹丸接触位置的速度与弹丸上接触点位置的速度相同,钢筋在接触点形成一个不动塑性铰,在两侧形成2个移动塑性铰,因此钢筋和混凝土之间在流体密实区内将形成相对的速度场:

(7)

式中:x为弹丸与钢筋碰撞初始时刻钢筋上各点到碰撞接触点的距离。

在图5钢筋受力模式下,单根钢筋将会产生如下作用力:

(8)

Wen H M[11]用等效应变判断受冲击载荷的固支梁的失效,等效应变由轴向应变和切应变组成。本文研究的弹丸半径与钢筋小梁的长度是相同量级的,忽略了剪切应变对等效应变的影响。等效应变即可单独用梁的轴向应变来表示。轴向应变由2项组成,即钢筋的总的轴向应变为

(9)

式中:εm为膜应变,εb为弯曲应变。

当轴向应变大于钢筋失效应变时,钢筋断裂,钢筋对弹丸的阻力为0。

本文主要采用球形空腔膨胀理论来计算混凝土介质对钢筋和弹丸的阻力[12-15]。弹丸头部受混凝土介质在接触表面法向的应力为

将阻应力在弹头表面积分,计算出混凝土介质在弹丸轴向方向的总的阻力:

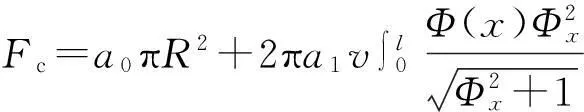
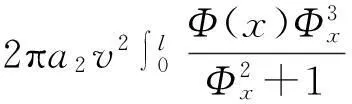
式中:v为弹丸轴向侵彻速度,Φ(x)为弹丸头部形状函数。

2模型分析

2.1　实验验证

本文假设弹丸垂直侵彻钢筋混凝土靶板时弹丸为刚性,不考虑侵蚀对模型的影响,弹丸撞击点为网眼中心。特别地,钢筋网层都是理想分布,每一层钢筋网都严格对齐,忽略因撞击点位置不同而受力不对称对弹丸的偏转影响。本文模型与实验的比较如图7所示,模型计算结果与实验符合较好。

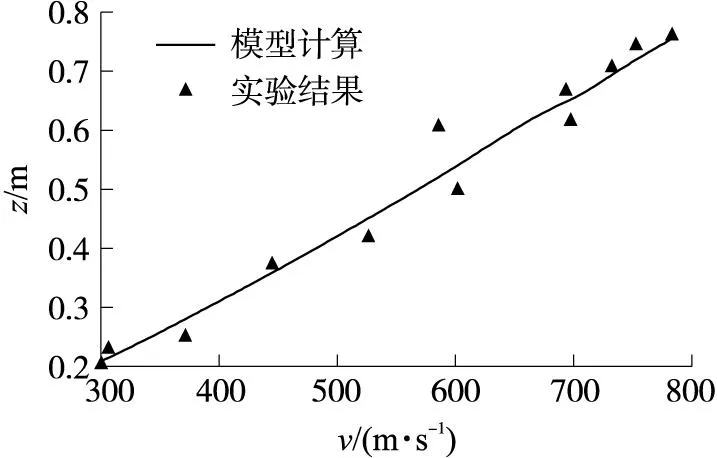
图7　模型预测与实验值的对比

为了研究钢筋配筋率对弹丸侵彻的影响,本文进行了4种配筋率的弹丸侵彻钢筋混凝土的实验,弹丸速度在750~1 250 m/s范围内。实验后发现弹丸无明显质量损失,因此本文刚性弹假设在此处满足计算要求。

钢筋参数:第1层钢筋距混凝土的表面距离为50 mm,从第2层钢筋开始余下的钢筋网层都是以一定间距均匀分布,网眼尺寸(w)为50 mm×50 mm,钢筋网格间距D有4种情况:225 mm,115 mm,75 mm,55 mm,分别对应着4种不同的体积配筋率,即0.5%,1.0%,1.5%和2.0%。

现代信息技术，特别是信息化、智能化普及的时代，这就为“以学习者为中心”的新观念提供了很好的硬件环境，这种观念还需要引导和强调可以帮助同学们，同时引导他们学会检索更有用有价值的信息，也要学会分辨正确和错误的信息等知识，更要学会遇到问题可以自己解决的能力。培养学生的财务思维模式，不仅仅学会教材的知识就可以，最后做到举一反三的推断能力，培养他们的批判性和创造性思维，并提高他们的发展社会的交往和人际关系。

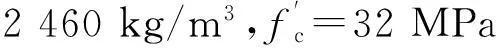
图8显示了实验值与模型计算的对比。由图可见,对于模型计算结果，在4种配筋情况下，配筋率越高,侵彻深度越小;在低速范围内配筋率对侵彻的影响较小;在高速范围,配筋率的影响才会显现。

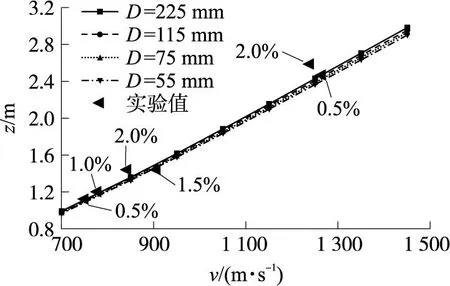
图8　本文实验与模型对比

2.2　钢筋参数分析

根据本文实验钢筋混凝土靶体参数和弹丸参数,对弹丸侵彻钢筋混凝土模型进行参数分析。弹丸侵彻钢筋位置分为4种情况,4种撞击点位置示意图如图9所示。

图9　弹着点在钢筋网层中位置示意图

对于刚性弹丸侵彻半无限靶,当钢筋均匀分布时,随着弹丸撞击速度的增大,弹丸撞击到钢筋的层数也在增加,钢筋对弹体侵彻深度的影响不断增大。体积配筋率小于2%,撞击速度在1 000 m/s以下时,钢筋对侵彻的影响很小。为了能够显示出钢筋在侵彻中的影响规律,本文着重分析侵彻速度在800~1 800 m/s范围内的影响规律。

采用同一直径(d=6 mm)钢筋,不同钢筋网层间距对侵彻深度的影响如图10(a)所示。可以看出,随着弹丸撞击速度的增加,网层间距越小,侵彻深度越小。而随着侵彻速度增大,不同网格间距对侵彻深度的影响越明显。

图10(b)显示了不同钢筋直径d下的侵彻速度与侵彻深度的关系,钢筋直径越大,则钢筋对侵彻的影响越大,侵彻深度越小。计算结果显示,速度为1 750 m/s时,直径6 mm 的钢筋的侵彻深度为3.70 m,直径30 mm的钢筋的侵彻深度为3.10 m。钢筋直径越大,配筋率也在增大,钢筋对弹丸阻力也就越明显。

当撞击点位置不同时,比较弹丸分别侵彻钢筋节点、网眼、单根钢筋中点情况下不同撞击速度下的侵彻深度,如图10(c)所示。图10(c)中3种不同情况下的3条曲线接近重合,说明在d=6 mm,D=225 mm情况下(体积配筋率为0.5%),弹丸撞击点位置影响不明显。而当d=30 mm,D=55 mm时,3种情况就有明显的不同,如图10(d)所示。侵彻在钢筋节点时侵彻深度要比侵彻在单根钢筋中点的侵彻深度小;而对于侵彻网眼为50 mm×50 mm的钢筋网眼处,侵彻深度要小于其他2种情况。

d和D不同,钢筋混凝土的配筋率则不同。下面研究在同一配筋率下d与D对侵彻的影响。对于体积配筋率2%有2种情况:情况一为d=6 mm,D=55 mm;情况二为d=12 mm,D=225 mm。图11显示了2种情况的计算结果,计算结果表明,同一配筋率下,采用小直径的配筋方式更不利于弹体的侵彻。

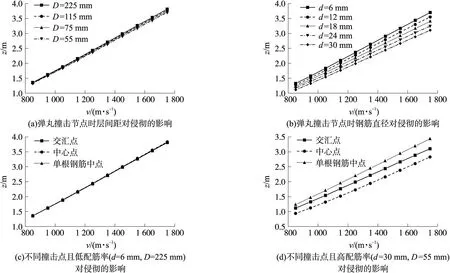
图10　侵彻深度与撞击速度关系曲线

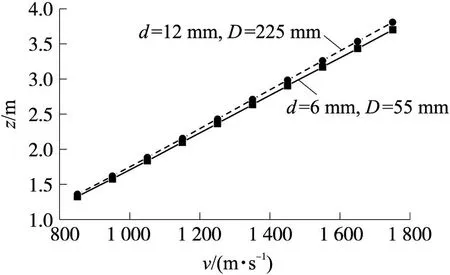
图11　相同配筋率下不同d和D对侵彻深度的影响

3结束语

本文在Forrestal研究的尖卵形弹丸侵彻钢筋混凝土模型的基础上,对实验取出的断裂钢筋进行了宏观和细观分析,确定了钢筋的受力模式,建立了考虑钢筋对弹丸阻力的侵彻钢筋混凝土模型。分析了钢筋直径、网层间距以及撞击点位置对侵彻的影响。特别比较了相同配筋率下的2种不同配筋方式对侵彻的影响,提出了一种更利于防护的配筋方式。本文模型与实验值的比较显示了模型的有效性,本文研究为军事目标的防护设计提供了理论依据。

参考文献

[1] RIERA J D.Penetration,scabbing and perforation of concrete structures hit by solid missiles.Nuclear Engineering and Design,1989,115(1):183-203.

[2] DANCYGIER A N.Effect of reinforcement ratio on the resistance of reinforced concrete to hard projectile impact.Nuclear Engineering and Design,1997,172(1):233-245.

[3] CHEN X W,LI X L,HUANG F L,et al.Normal perforation of reinforced concrete target by rigid projectile.International Journal of Impact Engineering,2008,35(10):1 119-1 129.

[4] LUK V K,FORRESTAL M J.Penetration into semi-infinite reinforced-concrete targets with spherical and ogive nose projectiles.International Journal of Impact Engineering,1987,6(4):291-301.

[5] 欧阳春,赵国志,杜中华,等.弹丸垂直侵彻钢筋混凝土介质的工程解析模型.爆炸与冲击,2004,24(3):273-277.

OUYANG Chun,ZHAO Guo-zhi,DU Zhong-hua,et al.An engineering analytical model for projectiles to penetrate normally into semi-infinite reinforced concrete targets.Explosion and Shock Waves,2004,24(3):273-277.(in Chinese)

[6] 穆朝民,任辉启.弹丸对钢筋混凝土中钢筋交汇处侵彻效应研究.高压物理学报,2010,24(5):351-358.

MU Chao-min,REN Hui-qi.Research on the effect of the projectile penetrating into reinforced concrete targets at the intersection of steel bar..Chinese Journal of High Pressure Physics,2010,24(5):351-358.(in Chinese)

[7] 葛涛,王明洋.坚硬岩石在强冲击载荷作用近区的性状研究.爆炸与冲击,2007,27(4):306-310.

GE Tao,WANG Ming-yang.Character near strong impact loading zone in hard rock.Explosion and Shock Waves,2007,27(4):306-311.(in Chinese)

[8] 王明洋,邓宏见,钱七虎.岩石中侵彻与爆炸近区问题研究.岩石力学与工程学报,2005,24(16):2 859-2 863.

WANG Ming-yang,DENG Hong-jian,QIAN Qi-hu.Study on problems of near cavity of penetration and explosion rock.Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2 859-2 863.(in Chinese)

[9] 葛涛,王明洋,王晓军.弹体冲击混凝土半无限的侵彻阻力与深度计算.振动与冲击,2008,27(1):107-110.

GE Tao,WANG Ming-yang,WANG Xiao-jun.Hydrodynamic model for concrete targets under impact of a projectile:resistance and depth of penetration.Journal of Vibration and Shock,2008,27(1):107-110.(in Chinese)

[10] SATAPATHY S.Application of cavity expansion analysis to penetration problems.Austin,USA:The University of Texas,1997.

[11] WEN H M,REDDY T Y,REID S R.Deformation and failure of clamped beams under low speed impact loading.International Journal Impact Engineering,1995,16(3):435-454.

[12] FORRESTAL M J,TZOU D Y.A spherical cavity expansion penetration model for concrete targets.International Journal of Solids and Structures,1997,34:4 127-4 146.

[13] STAPATHY S.Dynamic spherical cavity expansion in brittle ceramics.International Journal of Solids and Structures,2001,38:5 833-5 845.

[14] 穆朝民,任辉启.弹丸对混凝土中钢筋结构侵彻效应研究.兵器材料科学与工程,2011,34(6):1-5.

MU Chao-min,REN Hui-qi.Research on the effect of the projectile penetration into the reinforced concrete targets at the intersection of the steel bar.Chinese Journal of High Pressure Physics,2011,34(6):1-5.(in Chinese)

[15] 周宁,任辉启,沈兆武,等.卵形头部弹丸侵彻钢筋混凝土的工程解析模型.振动与冲击,2007,26(4):73-76.

ZHOU Ning,REN Hui-qi,SHEN Zhao-wu,et al.Engineering analytical model for ogive-nose projectiles to penetration into semi-infinite reinforced concrete targets.Journal of Vibration and Shock,2007,26(4):73-76.(in Chinese)

[16] CANFIELD J A,CLATOR I G.Development of a scaling law and techniques to investigate penetration in concrete.Dahlgren,VA:US Naval Weapons Laboratory,1966.