带末端角度约束的多导弹协同制导律设计

带末端角度约束的多导弹协同制导律设计

惠耀洛1,南英1,陈哨东2,马晓华1

(1.南京航空航天大学 航天学院,南京 210016;2.国家光电重点实验室,河南 洛阳 471009)

摘要:为了实现饱和攻击与饱和防御,提出了一种针对机动目标的多导弹协同制导律。建立了视线坐标系下的弹目相对运动数学模型,设计了三阶扩张状态观测器,对目标机动加速度项和运动方程中的耦合项进行观测与跟踪。在导弹飞行前段,基于滑模变结构理论设计了攻击时间可控的多导弹时间协同制导律;在导弹攻击末段,基于有限时间控制理论设计了满足终端角度约束的制导律,给出了导引律切换条件。仿真结果表明:该复合导引律能够使多枚导弹在满足攻击末端角度约束的条件下实现攻击时间协同;该制导律采用完备的空空导弹轨迹控制系统进行仿真,能够满足实际工程应用的要求。

关键词:机动目标;时间协同制导;末端角度约束;滑模变结构控制;状态观测器

中图分类号:TJ765.3文献标识码:A

收稿日期:2015-03-30

作者简介:侯博(1991- ),男,硕士研究生,研究方向为飞行器制导与控制系统设计。E-mail:houbo0601@163.com。

通讯作者:宋建梅(1968- ),女,博士生导师,副教授,研究方向为飞行器制导与控制系统设计。E-mail:sjm318@bit.edu.cn。

Cooperative Guidance Law for Multiple Missiles With

Terminal Impact Angle Constraint

HUI Yao-luo1,NAN Ying1,CHEN Shao-dong2,MA Xiao-hua1

(1.College of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.Science and Technology on Electro-optic Control Laboratory,Luoyang 471009,China)

Abstract:A cooperative guidance law was proposed for multiple missiles in order to attack or defense against maneuvering targets at the same time.The equation of missile-target relative motion was established in sight line coordinate-system,and the third-order extended state observer was designed to observe and track acceleration of targets and coupling terms in the motion equation.The 4D impact-time control guidance law(ITCG)was designed in the forepart of interception based on the sliding mode control theory to ensure the attack time to be controlled.In the terminal ballistic trajectory,another guidance law based on the finite time control theory was designed to meet the terminal angle constraint.Switching conditions of guidance law was also designed considering aspects of time and space.Numerical simulation results show that the attack time of multiple missiles is basically the same under the terminal attack angle constraint,and this guidance law can be used to combat maneuvering targets.The simulation is conducted using complete model of air-to-air missile,and this guidance law can be applied in actual projects.

Key words:maneuvering target;time-cooperative guidance;terminal angle constraint;sliding mode variable structure control;state observer

随着精确制导武器攻防对抗技术水平的不断提高,饱和攻击与饱和防御逐渐成为行之有效的对抗策略,其核心问题即为实现多飞行器协同制导和协同攻击[1-2]。

实现饱和攻击与饱和防御,其一要求多导弹攻击时间协同,其二要满足特定的约束条件(终端速度约束、角度约束等)。有关多弹协同制导律方面的研究,文献[3]在传统PNG制导律的基础上,引入弹着时间反馈误差,推导了多弹时间协同制导律(ITGC)。文献[4]在文献[3]的基础上将末端角度控制问题转化为满足约束条件的最优控制问题进行求解,得到了具有末端角度约束的时间协同制导律。文献[5]基于协同控制理论,引入流形宏函数和流形的期望动态特性函数,设计了带终端约束的制导律。文献[6]基于动态逆系统理论,从距离协同的角度出发研究时间协同,设计了距离协同制导律。文献[7]采用双圆弧原理规划导弹航路,设计导弹按照圆弧轨迹机动的指令,实现攻击时间协同。文献[8]通过改进比例制导律,设定导弹在特定攻击航路点上的航迹角,实现了同时满足攻击角度和攻击时间约束的制导律。文献[9]提出了一种时间协同分布式导引律设计方法。文献[10]通过设计虚拟导引点的运动轨迹以及导弹与导引点间相对距离变化律,实现了多弹速度、时间、位置和角度协同。上述文献大多针对低速、不机动目标,一般需要估计导弹剩余飞行时间。为满足实际工程应用要求,有必要采用完备的导弹系统模型,开展三维平面内针对机动目标的多导弹协同制导律研究。

针对机动目标的跟踪,卡尔曼滤波技术[11]是一种常用的方法,但其算法复杂,且需要精确知道系统模型和噪声统计特性,不利于在导弹攻防对抗过程中使用。本文首先推导了在视线坐标系下的弹目相对运动方程,对系统扰动设计了三阶扩张状态观测器。然后设计了基于滑模变结构控制理论的多导弹时间协同制导律,在弹着时间可控的基础上实现了多弹时间协同。在导弹攻击末段,采用有限时间控制理论设计了满足终端角度约束和视线角速率快速收敛的末段制导律。仿真结果表明,上述制导律能够使多枚多弹在满足终端攻击角度约束的同时实现时间协同,并且能够对机动目标实现高精度拦截。

1基于视线坐标系的弹目相对运动数学模型

视线坐标系的原点O取在导弹的瞬时质心上,OxL轴与导弹视线重合;OyL轴位于包含导弹视线的铅垂面内垂直于OxL轴,指向上为正;OzL轴垂直于其他两轴并构成右手坐标系。定义视线高低角qθ为导弹视线与水平面之间的夹角,视线方位角qψ为导弹视线在水平面内投影与地面坐标系Ax轴之间的夹角。

根据坐标转换理论[12],可得地面坐标系与视线坐标系的转换关系:

(1)

式中:

(2)

视线坐标系相对于地面坐标系的旋转角速度ΩL为

(3)

用iL,jL,kL分别表示视线坐标系中3个轴向的单位向量,则在导弹攻击目标的过程中导弹和目标相对距离R可以表示为

R=RiL

(4)

在地面坐标系中导弹和目标接近速度和接近加速度分别为

(5)

(6)

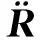
(7)

式中:aMr,aMθ,aMψ分别为导弹加速度在视线坐标系三轴上的分量;aTr,aTθ,aTψ分别为目标加速度在视线坐标系三轴上的分量。

由式(6)和式(7)得:

(8)

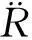
2基于扩张状态观测器的多导弹协同制导律设计

本文针对系统模型中的视线角耦合项和目标加速度项,设计了三阶扩张状态观测器,对系统已知和未知总扰动进行观测和估计,然后设计了多导弹协同制导律:多枚导弹首先在时间协同制导律导引下攻击目标,达到制导律切换条件后,转为末端角度约束制导律。因为在攻击末段多枚导弹已经基本实现时间协同,同时角度约束控制可以在较短时间内完成,因此该复合制导律可以使多枚导弹在满足末端攻击角度约束的情况下实现时间协同,饱和攻击目标。

2.1　基于ESO的系统总扰动的估计

由式(8)得:

(9)

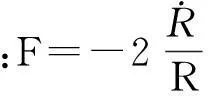
(10)

根据ESO理论[13],对系统(10)设计如下的扩张状态观测器:

(11)

2.2　末端角度约束制导律设计

引理1[14]二阶线性系统

(12)

可被下列形式的状态反馈控制器在有限时间内镇定:

(13)

假设导弹在攻击末端期望的视线高低角和视线方位角分别为qθd,qψd，以纵向平面内的运动为例，取

qd=qθd

(14)

增加状态变量x0=x1-qd,得到新系统:

(15)

反馈线性化上述状态方程,令u=U-(Fx2+f),带入式(15),得到:

(16)

根据引理1,针对如式(6)所示的系统,可取控制量:

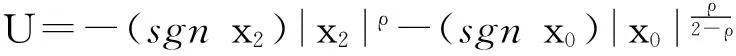
(17)

则x0和x2将在有限时间内被镇定到0,即x1→qd,x2→0,导弹在满足末端角度约束的条件下准平行接近于目标。

将式(17)带入式(8),并由扩张状态观测器求得系统扰动值，得到末端角度约束制导律的表达式:

(18)

式中:ρ1,ρ2为制导律参数;z31,z32为系统扰动观测值。

2.3　时间协同制导律设计

根据文献[3],多枚导弹协同攻击时间td应满足:

(19)

式中:tl为第l枚导弹单独打击目标时的最短攻击时间。

设计滑模面和自适应滑模趋近律:

s=R[x2+(td-t)sgnx2]

(20)

(21)

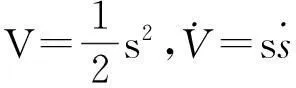
由式(20)和式(21)可得:

(22)

将式(22)带入式(8),可得:

(23)

式中:k1,k2，ε1,ε2分别为相应的比例系数。

综上所述,多枚导弹协同攻击目标时,飞行前段采用多弹攻击时间协同制导律,飞行末段采用终端角度约束的制导律。由于拦截末段各拦截弹已基本达到时间协同,最终的拦截攻击也几乎同步进行,同时,在末段快速调整攻击角度可以满足末端攻击角度约束。考虑时间和空间两方面设置导引律切换条件,在空间上如果弹目距离满足R=Rm或者攻击时间t=0.9td,导弹开始由时间协同制导律切换为终端角度约束制导律。为减小导弹在飞行过程中过载的抖动,用饱和函数替换符号函数,得到导弹的总制导指令:

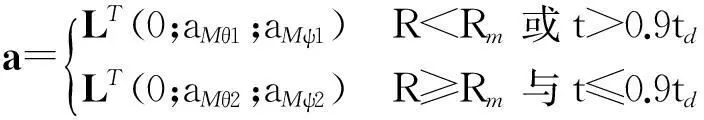
(24)

其中饱和函数采用如下形式:

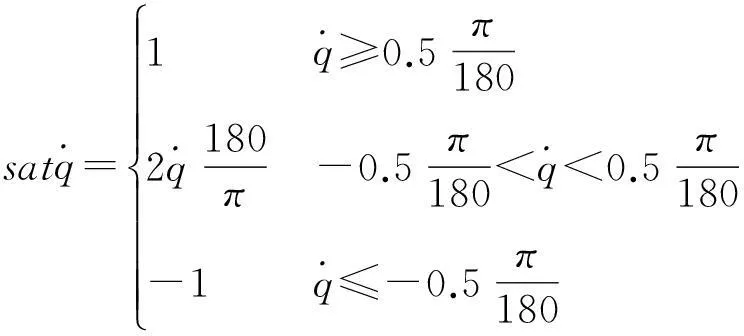
(25)

3仿真与分析

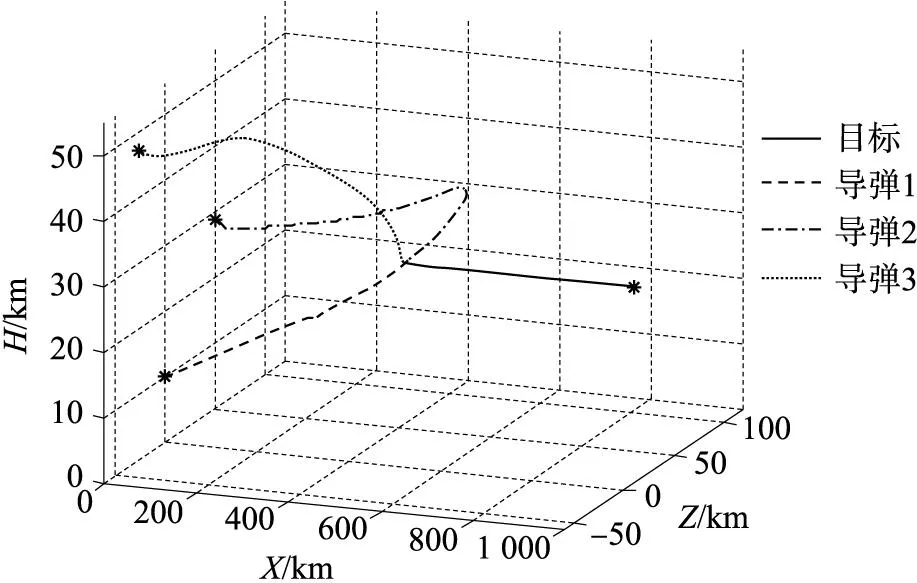
图1　导弹和目标三维飞行轨迹

对仿真结果进行分析。

①由图1和图2知,为实现协同攻击目标,3枚导弹均做了相应的机动飞行而不是直接攻击目标。导弹1和导弹2主要在水平面内机动飞行,导弹3主要在铅垂面内机动飞行。在水平面内导弹1和导弹2分别沿z轴正向和负向做大转弯机动后攻击目标,而导弹3在水平面的弹道比较平直;在铅垂面内导弹3与导弹1和导弹2相比距离目标更近且位于目标上方,其在铅垂面内爬升机动飞行后俯冲攻击目标,而导弹1和导弹2在铅垂面内的弹道比较平直。

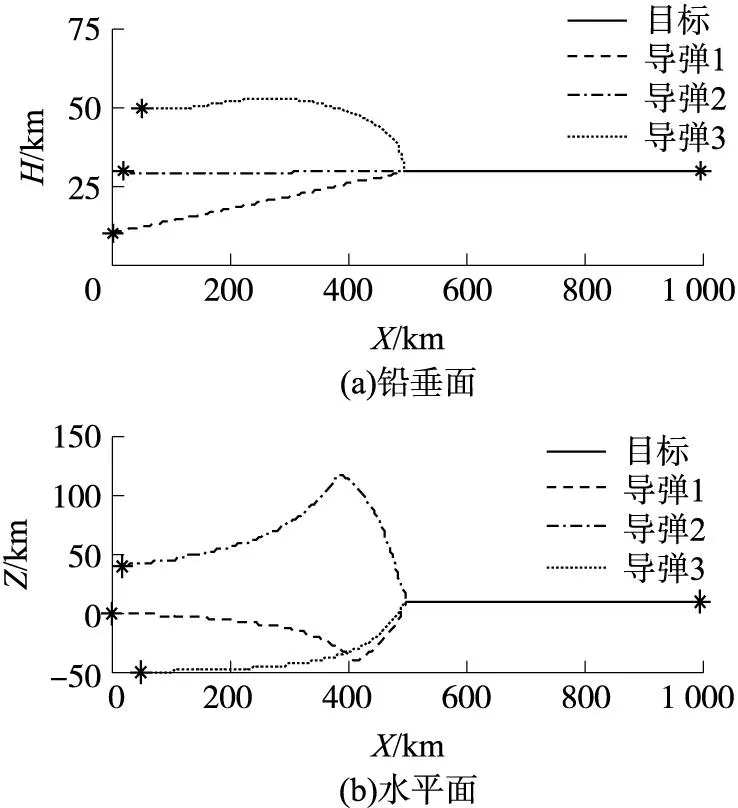
图2　弹目飞行轨迹在铅垂面和水平面内的投影

②由图3和图4知,因3枚空空导弹采用相同的发动机模型,载机发射后均先做加速运动,直至发动机工作结束。随着飞行时间增加,导弹速度逐渐下降。导弹3在150s左右开始降高飞行,飞行末段俯冲攻击目标,因此其末端速度显著增加。3枚导弹与目标的距离均逐渐减小,并且实现了精确命中,全程飞行时间分别为249.3s,250.1s和248.6s,最大协同时间误差为1.4s,基本实现了攻击时间协同。

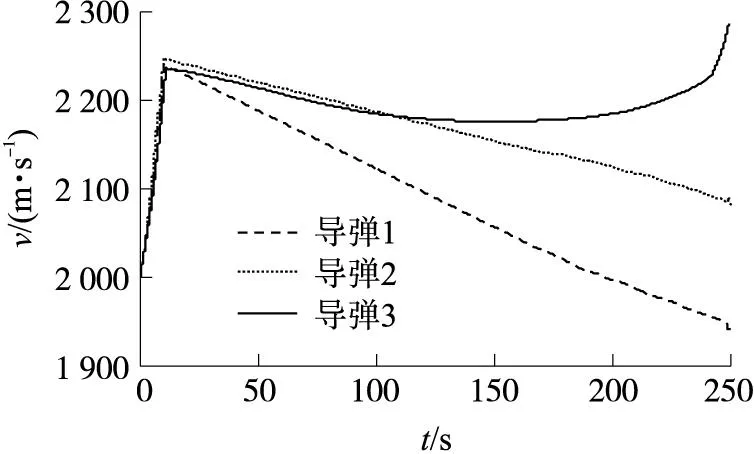
图3　导弹速度随时间变化曲线

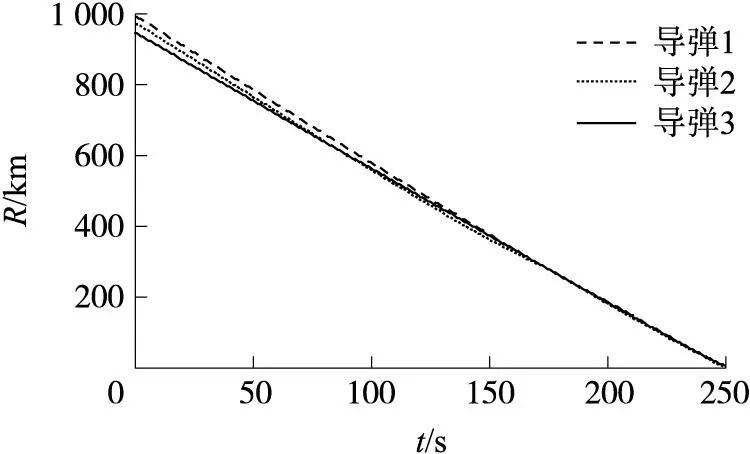
图4　弹目距离随时间变化曲线

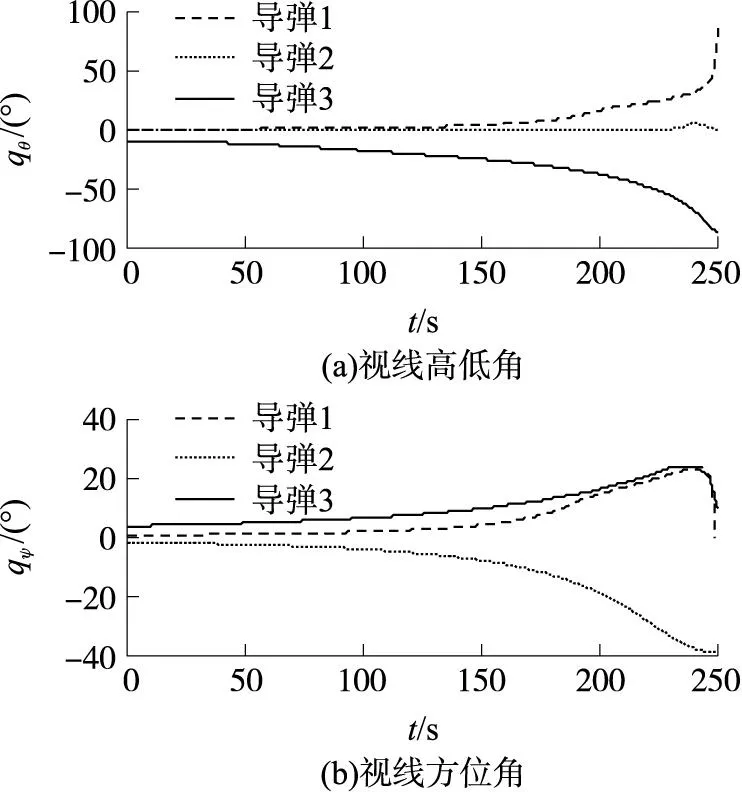
图5　视线高低角和视线方位角随时间变化曲线

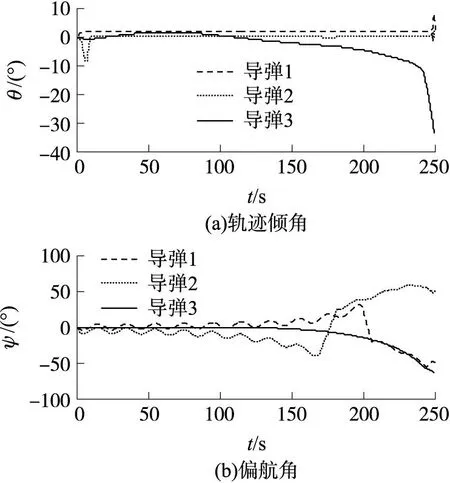
图6　导弹轨迹倾角和偏航角随时间变化曲线

③由图5知,3枚导弹攻击末端的视线角分别为(86.3°,1.2°),(0.9°,-38.8°)和(-84.2°,10.7°),最大角度偏差为1.3°,满足终端角度约束要求。由图6知，导弹轨迹倾角θ和轨迹偏角ψ随时间变化趋势与视线角随时间的变化趋势大致相同。在制导律作用下,如果控制时间足够长,导弹的轨迹角将与视线角相一致。

④由图7知,目标在水平面内作SIN型机动,引起导弹在水平面的过载波动,但导弹3在水平面内的过载波动较小,原因是导弹3在z轴方向偏离目标初始位置较远,且导弹整体速度较大,导弹机动对其制导指令影响相对较小,因此其在水平面内的弹道相对平直。末段切换制导律后,3枚导弹的机动过载均增大,但都在导弹可用过载范围之内,能够满足命中精度的需求。

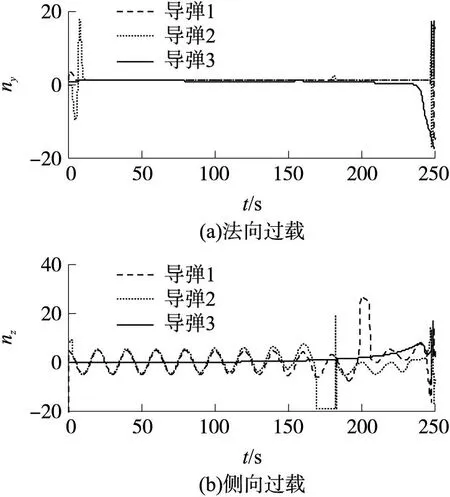
图7　导弹法向过载和侧向过载随时间变化曲线

4结论

针对机动目标在三维平面内的多导弹协同制导律问题,本文首先设计了三阶扩张状态观测器,对目标加速度项和视线角耦合项进行估计和跟踪;其次,在导弹飞行前段基于滑模变结构理论设计了攻击时间可控的多导弹时间协同制导律,通过导弹在三维平面内的机动飞行实现攻击时间基本协同;最后,在导弹攻击末端,基于有限时间控制理论设计了满足终端角度约束的末段制导律,并控制视线角速率趋近于0。本文提出的针对机动目标的协同制导律,采用完备的空空导弹轨迹控制系统模型进行仿真和分析,能够满足实际工程应用的要求。

参考文献

[1] 黄国强.多飞行器协同轨迹优化设计.现代防御技术,2015,43(1):160-167.

HUANG Guo-qiang.Optimal design of cooperative trajectories for multiple flight vehicles.Modern Defence Technology,2015,43(1):160-167.(in Chinese)

[2] 王宏,王君,梁文波,等.新一代空空弹多弹协同攻击制导策略.航空兵器,2011(2):7-11.

WANG Hong,WANG Jun,LIANG Wen-bo,et al.Multi-missile cooperative attacking strategy of new type of aie-to-air missile.Aero Weaponry,2011(2):7-11.(in Chinese)

[3] JEON I S,LEE J I,TAHK M J.Impact-time control guidance law for anti-ship missiles.IEEE Transactions on Control Systems Technology,2006,14(2):260-266.

[4] LEE J I,JEON I S,TAHK M J.Guidance law to control impact time and angle.IEEE Transactions on Aerospace and Electronic System,2007,43(1):301-310.

[5] 肖增博,雷虎民.导弹制导的协同控制方法.航空兵器,2012(1):18-24.

XIAO Zeng-bo,LEI Hu-min.Synergetic control approach to missile guidance.Aero Weaponry,2012(1):18-24.(in Chinese)

[6] 王晓芳,郑艺裕,林海.多导弹协同作战制导律研究.弹道学报,2014,26(1):61-66.

WANG Xiao-fang,ZHENG Yi-yu,LIN Hai.Research on guidance law for cooperative attack of multiple missiles.Journal of Ballistics,2014,26(1):61-66.(in Chinese)

[7] 张友根,张友安,施建洪,等.基于双圆弧原理的协同制导律研究.海军航空工程学院学报,2009,24(5):537-542.

ZHANG You-gen,ZHANG You-an,SHI Jian-hong,et al.Research on cooperative guidance for multi-missiles based on bi-arcs.Journal of Naval Aeronautical and Astronautical University,2009,24(5):537-542.(in Chinese)

[8] JUNG B Y,KIM Y D.Guidance laws for anti-ship missiles using impact angle and impact time//AIAA Guidance,Navigation,and Control Conference and Exhibit.Keystone,Colorado:AIAA,2006:1-13.

[9] 马国欣,张友安.多导弹时间协同分布式导引律设计.控制与决策,2014,29(5):843-847.

MA Guo-xin,ZHANG You-an.Time-cooperative distributed guidance law design for multi-missiles.Control and Decision,2014,29(5):843-847.(in Chinese)

[10] 王晓芳,郑艺裕.基于虚拟导引点的多弹协同作战控制方法.弹道学报,2013,25(3):6-12.

WANG Xiao-fang,ZHENG Yi-yu.A method of controlling multiple-missiles combating cooperatively based on fictitious guidance dot.Journal of Ballistics,2013,25(3):6-12.(in Chinese)

[11] 张功,李帆,赵建辉,等.弹着时间可控的机动目标多弹协同制导律.指挥控制与仿真,2010,32(1):52-55.

ZHANG Gong,LI Fan,ZHAO Jian-hui,et al.Impact-time-control guidance law for multi-missile cooperative model with mobility of the target considered.Command Control & Simulation,2010,32(1):52-55.(in Chinese)

[12] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学.北京:北京理工大学出版社,2000.

QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile flight mechanics.Beijing:Beijing Institute of Technology Press,2000.(in Chinese)

[13] 韩京清.自抗扰控制技术.北京:国防工业出版社,2009.

HAN Jing-qing.Auto/active disturbances rejection control technology.Beijing:National Defense Industry Press,2009.(in Chinese)

[14] BHAT S P,BERNSTEIN D S.Finite-time stability of homogeneous systems.Advances in Stability,1997(4):2 513-2 514.