基于样条拟合模型的古塔变形分析

基于样条拟合模型的古塔变形分析

燕岩军

(山西机电职业技术学院，山西 长治，046011)

摘要：基于2013年全国大学生数学建模C题数据，对古塔变形做初步判断。首先，根据数据绘制出等高线图，对塔体的倾斜、弯曲情况进行定性分析。然后，对各层的重心建立样条拟合模型，计算塔体倾斜位移和倾斜度。最后，根据2009年、2011年的数据，对古塔变形做出预测：塔体的变形会逐年加重。

关键词：古塔；倾斜观测；样条拟合；变形分析

收稿日期：2014-11-07

作者简介：燕岩军(1984-)，山西长治人，山西机电职业技术学院助教、硕士.

中图分类号：O29文献标识码：B

1数据

本文所用数据来自2013年全国大学生数学建模C题，数据来源中国某重点文物古塔分别于1986年7月、1996年8月、2009年3月和2011年3月先后4次观测结果。

2模型建立与求解

2.1模型假设

假设1：塔体各层假定为密度均匀的匀质体，塔体每一层的重心与中心重合；

假设2：在观测期内，古塔周围地质稳定无沉降或隆起，不影响监测点；

假设3：古塔仅有唯一塔尖，且塔尖为古塔的海拔最高点；

假设4：采样数据真实反映古塔状态；

2.2 模型的建立与求解

2.2.1 计算中心坐标

依据假设及四年的古塔数据，求解中心坐标，建立如下模型：

运用lingo软件计算最优值，得出四年每一层的中心坐标。将每一层中心坐标一一代入数据即可得出。其结果分别如下：

表1　历年古塔各层中心坐标

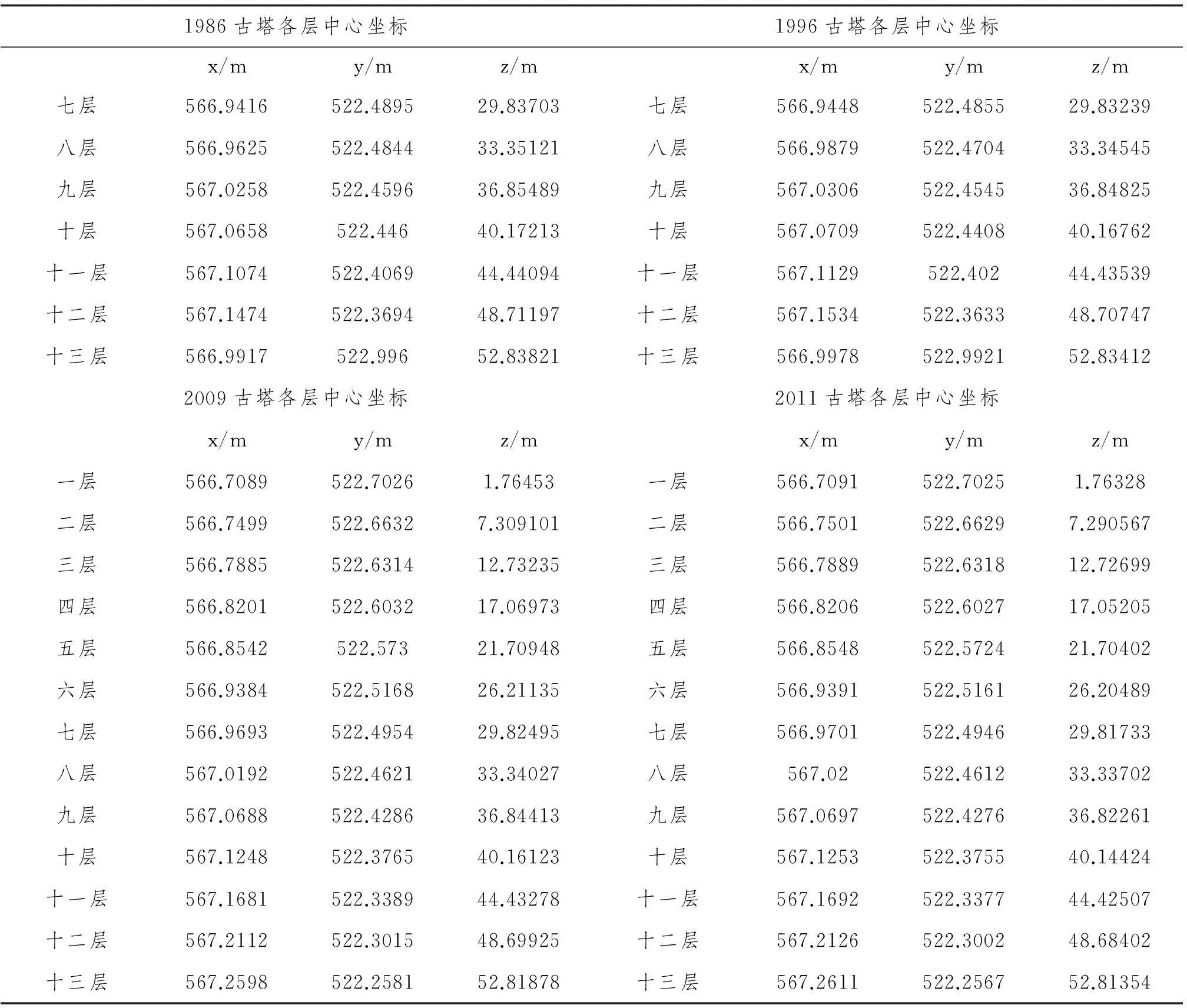
续表1　历年古塔各层中心坐标

2.2.2 塔体重心轴线投影模型的计算模型

为研究简便，本文将历年中心投影到xoy，xoz，yoz平面下研究，观察其中心在三个不同投影面上变化趋势。由于在三个平面上投影大致也呈现S型变化，本文主要通过拟合法中三次样条插值函数来估计变化趋势。本文以1986年中心坐标投影到xoy平面为例，数据拟合出三次样条函数[1]，模型如下：

投影到xoz，yoz平面以及其它年份拟合相类似，这里不一一介绍，拟合程序如下[2]：

% M文件,求拟合图线，及多项式系数

function output = msline(x,y)

%x，y为拟合数据向量

Pp=spline(x,y) %返回样条插值的分段多项式(pp)形式结构

Fnplt(pp) %画出样条拟合图线

2.2.3 倾斜计算

拟合得到底层处中心坐标和塔尖坐标；其中，通过计算空间凸八边形的中心坐标得到底层处中心坐标，塔尖坐标取历年测量的最高点(z坐标最大值点)。计算过程中，为了保证计算精度，过程数据取8位有效数字。

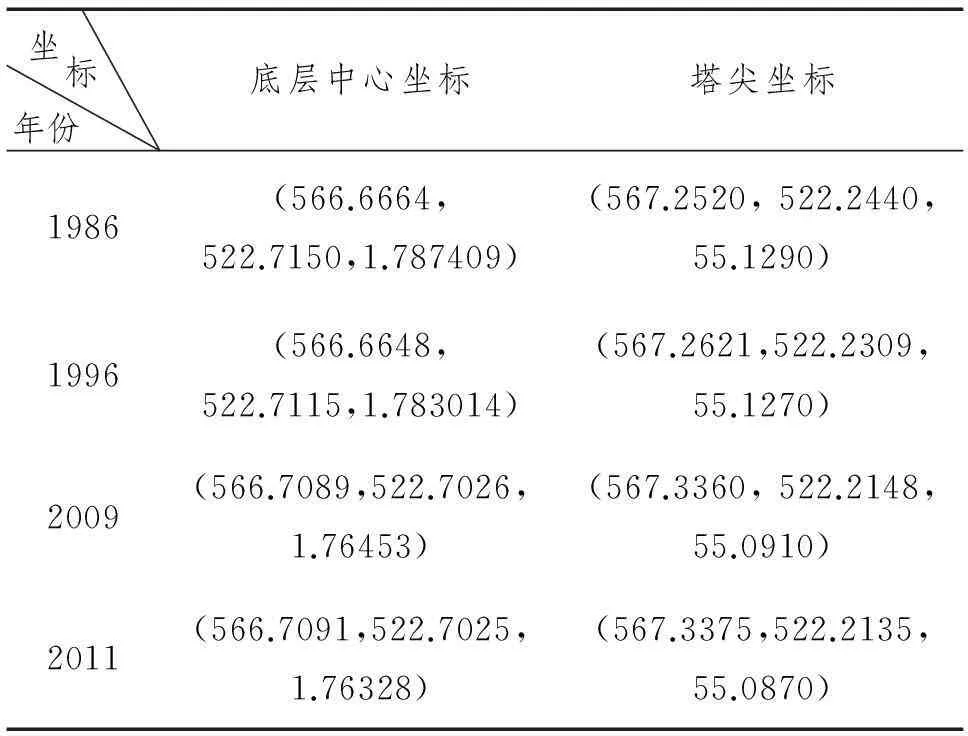
表2　古塔历年底层中心坐标塔尖坐标拟合数据

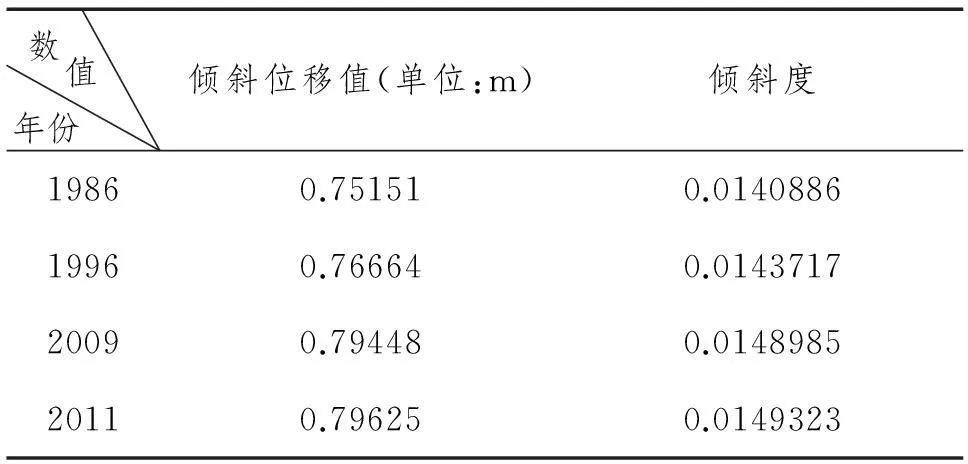
表3　历年倾斜位移值倾斜度

2.2.4 由各层半径变化情况，分析塔体变形情况

塔体变形，每一年每一层半径都在发生改变。Matlab数据拟合出每年每一层半径值，根据每一年每一层半径的相对变化量分析塔体变形趋势[4]，其每一年每一层半径值见下表：

表4　1986年和2011年各层半径变化情况(单位：m)

从表可以看出，每一年每一层半径都在改变，且相对于1986年的变化量6层最为明显，由此可以得出6层塔体坍塌现象显著，呈扩大趋势。

2.2.5 塔体倾斜预测

为研究塔体未来倾斜趋势程度，本文从四年的倾斜度方面来考虑(倾斜度在倾斜计算中已求出)。Matlab绘制出时间与倾斜度的点图，观测倾斜度趋势，如图：

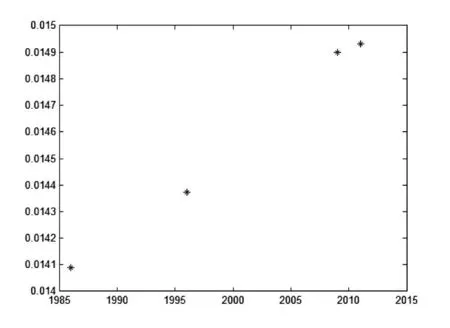
图1　时间与倾斜度关系图

可以看出，倾斜度与时间比较符合一次线性关系，可知，未来时间内，塔体倾斜会比较严重。由于倾斜度足够小，拟合效果会很差，这里为处理简便，论文将倾斜度变为原来的1000倍处理，即1986年，1999年，2009年，2011年的倾斜度分别为14.086,14.3717,14.8985,14.9323。根基数据拟合，拟合出一次线性方程为：

y=0.035x-55.5128

则根据此方程即可得到未来任意一年的倾斜程度(倾斜度缩小1000倍)。以2020年为例，计算出倾斜度值为15.1872，所以2020年的实际倾斜度为0.0151872.。显然，改函数为增函数，所以未来若干年，古塔将严重倾斜。

2.2.6 分析历年观测数据的最高、最低点，进一步验证结果

根据四年数据，用Matlab 绘制出历年最高点及最低点变化趋势图，分别如下：

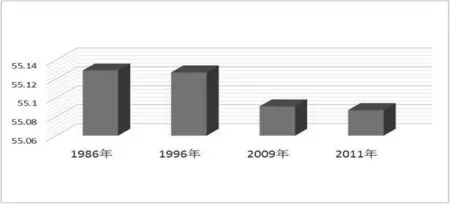
图2　历年最高点变化趋势

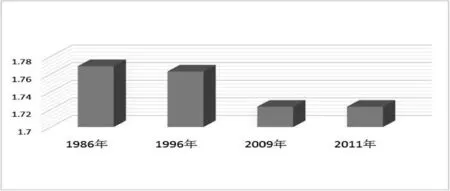
图3　历年最低点变化趋势

由此图可以得出，历年最高点最低点都呈递减趋势，因此，古塔将发生明显变形。

结论：综合以上预测及验证，可以知道古塔由于长时间承受自重、气温、风力等各种作用，以及长期自然因素影响，塔体自身倾斜会越来越严重，相关部门应该采取相应措施做好防护工作，防止古塔进一步被破坏。

3模型的优缺点及改进

3.1 模型的优缺点

优点：该模型给出的中心求解方法，计算简便且求解更科学、精确；利用三次样条插值函数数据拟合，图形直观明了，且拟合出结果更加符合实际，结论具有一定的真实性。

缺点：古塔有些数据缺失，如1986年，1999年13层，为了模型处理简便，该没有考虑，结果存在一定的误差

3.2 模型的改进

在模型的建立中，论文主要从将各层重心投影到各个平面上这方面来研究，这样简化了计算。如果能将模型转换为求解各层重心坐标的空间曲线方程，根据重心空间曲线方程样条进行数据拟合，进而求解其倾斜度，那么这样拟合求出的结果将更为精确。

参考文献：

[1]胡志晓.古塔倾斜观测和数据分析[J].江苏建筑，2011(6).

[2]石利情.关于高层建筑沉降及倾斜监测[J].科技创新导报，2012(18).

[3]许小勇.三次样条插值函数的构造与Matlab实现[J].兵工自动化，2006(11).

[4]刘慧颖.MATLAB7.0基础教程[M].北京：清华大学出版社，2008.

(责任编辑侯中岩)