基于微粒群算法的中制导弹道优化设计

基于微粒群算法的中制导弹道优化设计

邵雷1,雷虎民1,张建新2,赵宗宝1

(1 空军工程大学 防空反导学院,西安 710051;2 中国人民解放军786厂军代室,西安 710043)

摘要:为使拦截武器有效拦截目标,将直接多重打靶算法与微粒群算法相结合,设计了一种基于微粒群算法的中制导弹道优化算法。该算法借鉴直接多重打靶算法基本思想,将状态空间与参数空间分别进行分解与分段,并在此基础上结合中制导末端条件构建性能指标函数,将弹道优化问题转化为多目标优化问题;基于对指标函数之间依赖性的分析,在求解过程中将多目标优化分解为参数层和指标层优化两部分,采用微粒群算法对其进行分层优化求解。仿真研究表明,该优化算法能够对弹道进行有效优化。

关键词:弹道优化;多重打靶算法;微粒群算法;多目标优化

收稿日期:2014-02-11

基金项目:航空科学

作者简介:邵雷(1982- ),男,讲师,博士,研究方向为非线性控制、飞行器制导与控制。E-mail:shaoleijing@126.com。

中图分类号:V412.4文献标识码:A

Midcourse Guidance Trajectory Optimization Based on

Particle Swarm Optimization Algorithm

SHAO Lei1,LEI Hu-min1,ZHANG Jian-xin2,ZHAO Zong-bao1

(1.College of Air and Missile Defense,Air Force Engineering University,Xi’an 710051,China;

2.The Military Representative Office at 786 Factory of PLA,Xi’an 710043,China)

Abstract:To achieve the maximum kill probability in the target interception,the multiple shooting algorithm and the particle swarm optimization were combined,and a particle swarm optimization(PSO) algorithm was presented based on optimization algorithm of midcourse guidance trajectory.According to the idea of the multiple shooting algorithm,the proposed algorithm transformed the trajectory optimization to a multi-objective optimization problem by means of state space decomposition and endpoint constrain based on performance index.The multi-objective optimization problem was transformed to the optimization of parameter and performance index by analyzing the reliability between the two,and the PSO was employed to deal with the problem.The simulation result shows that the trajectory can be effectively optimized by the proposed algorithm.

Key words:trajectory optimization;multiple shooting algorithm;particle swarm optimization;multi-objective optimization

在防空作战中,飞行弹道是拦截武器综合性能的反应,决定了拦截武器能否命中目标。弹道优化是拦截武器设计的重要内容之一,沿着合理的弹道飞行有利于提高拦截武器的飞行品质,达到有效命中目标的目的。

弹道优化问题实际是根据给定的战技指标建立拦截武器运动方程,选择主要设计参数,构造性能泛函,并考虑在内点和边值条件约束的情况下,运用现代控制理论求解最优参数形成相应的飞行弹道。文献[1-2]中提出的多层次弹道优化方法,将整个飞行过程分为无控射入层、中制导层和末制导层3层,在不同层采用不同方法,以某一性能指标为依据寻求最优弹道。因此,弹道优化问题本质上是一种多学科优化问题。对于该类问题通常采用数值方法进行求解,这种求解方法大致可分为两大类:直接法和间接法。其中,直接法通过一定的算法在整个可行参数集中进行搜索,直到得到问题的优化解[4-5];间接法则基于最优控制理论,如极大值原理等,采用特定算法求取满足该最优性条件的最优解。相比之下,间接法求解结果更为准确,但求解过程通常较复杂,难以有效求解[6-7];直接法相对易于实现,但收敛时间较长,对搜索算法提出了一定的要求。文献提出的直接多重打靶算法能较好地求解飞行力学逆问题,但该算法收敛速度较低,难以用于实时控制;文献仅假定节点处的控制变量值,在一定程度上提高了收敛速度。针对上述问题,论文研究将微粒群算法(particle swarm optimization,PSO)与直接多重打靶算法相结合,基于直接打靶法的基本思想,将状态空间与控制参数进行区间分解,并对参数分段数量以及分段参数同时进行优化,将弹道优化问题转化为多目标优化问题,基于此采用微粒群算法优化算法进行分层优化求解。

1中制导弹道优化设计

1.1　拦截弹质点运动数学模型

考虑如下的拦截器纵向平面质点运动模型进行弹道优化计算:

(1)

式中:m,S分别为拦截器质量和参考面积;v为拦截器速度;FP为发动机推力;θ为弹道倾角;q为动压;g为重力加速度;Cx,Cy分别为阻力系数和升力系数;(x,y)表示拦截器在纵向平面内的坐标。其中:

(2)

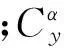
在实际飞行过程中,考虑到弹道的稳定性,通常对控制变量进行如下约束:

αmin≤α≤αmax

qmin≤q≤qmax

|n|≤nmax

式中:n为导弹过载;nmax为允许的最大过载。

1.2　优化问题描述

防空型拦截器通常在大气层内作战,这决定了拦截器射程有限,在设计拦截器飞行弹道时,不仅要保证导引头能够稳定跟踪目标,同时也希望拦截武器与目标相遇时具有较高的速度。为此,在中制导优化过程中,通常以末端速度最大为优化指标建立指标函数:

J(u(t))=φ(x(tf),tf)=-k1vf

式中:tf为终端时间。

考虑中末段交班条件,实质是对中制导末端提出了要求,进而对优化问题增加了末端约束条件。将末端状态约束作为罚函数带入上述指标函数,可以得到综合指标函数:

J1(u(t))=φ′(x(tf),tf)t)=-kvv(tf)+

ky|y(tf)-yf|+kx|x(tf)-xf|

(3)

式中:(xf,yf)表示中制导末端交班位置,为末端优化条件;kv≥0,ky≥0,kx≥0,表示约束权重,为无量纲量。

基于上述优化指标,可将中制导弹道优化问题转化为如下优化问题:

kx|x(tf)-xf|]

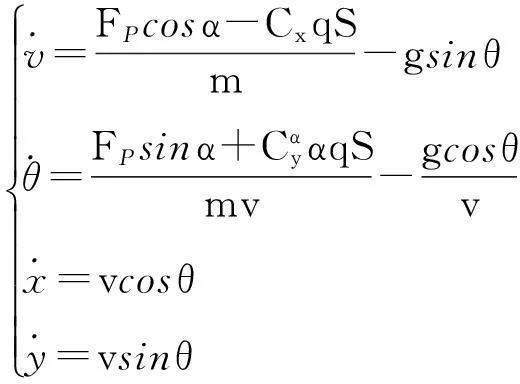
αmin≤α≤αmax

qmin≤q≤qmax

|n|≤nmax

(4)

2基于微粒群算法的中制导弹道优化算法

2.1　微粒群算法简介

基本PSO算法将每个个体看作是D维搜索空间中的一个没有体积的微粒,在搜索空间中以一定的速度飞行,微粒根据它本身的飞行经验以及同伴的飞行经验对速度进行动态调整。第i个微粒表示为Xi=(xi1xi2…xiD),它经历过的最好位置记为Pi=(pi1pi2…piD),也称为pbest。群体所有微粒经历过最好位置的索引号用符号b表示,即bbest。微粒i的速度用vi=(vi1vi2…viD)表示。对每一代,其第j维(1≤j≤D)根据如下方程变化:

vij(t+1)=wvij(t)+c1r1i[pij(t)-xij(t)]+

c2r2i[pg,j(t)-xij(t)]

(5)

xij(t+1)=xij(t)+vij(t+1)

(6)

式中:w为惯性权重;c1,c2为加速常数;r1i,r2i为2个在[0,1]范围内变化的随机函数。

为了摆脱局部最优点的吸引,保证收敛到全局最优,VandenBergh[10]提出了一般收敛PSO(GCPSO)对基本的PSO算法进行了如下改进。

令Xτ为全局最优微粒,则Xτ的速度和位置更新方式定义为

vτ,j(t+1)=-xτ,j(t)+pg,j(t)+wvτ,j(t)+

β(t)[1-2r2(t)]

(7)

xτ,j(t+1)=pg,j(t)+wvτ,j(t)+β(t)[1-2r2(t)]

(8)

式中:-xτ,j(t)项对微粒的位置进行重置;wvτ,j(t)项隐含重新搜索的方向;β(t)[1-2r2(t)]项保证重新搜索时微粒的速度不为0,r2(t)为[0,1]范围内变化的随机函数,β(t)为标量因子,其具体定义见文献[11]。

2.2　中制导弹道优化设计

对于式(4)中的弹道优化问题,直接打靶法是一种比较直接的方法,这种方法利用时间进行分段,将飞行器状态和控制变量进行参数化,将最优控制问题转化为参数优化问题直接求解,但该方法求解效率较低。本文研究借鉴该方法的基本思想,将该方法与微粒群算法相结合,对式(4)进行优化求解。首先,对优化变量关于距离进行分段,建立每一阶段的控制变量;其次,基于微粒群算法对分段数量以及分段参数进行优化。具体方式如下。

假定距离从0开始一直到中制导末端约束点结束,可建立如下分段区间:

[x1,x2,…,xN]

其中,N为分段数量,表示分段数为N-1段。

相应地,可建立每一段的控制变量区间:

[α1,α2,…,αN]

分段区间范围内的取值可以通过差值得到。基于上述分段方法可以得到整个飞行弹道的控制参数,通过解算可以得到这种分段方式以及该特定控制参数对应的性能指标J1。为此,优化性能指标J1实际上变为优化分段数量以及相应分段参数的问题。为了降低计算复杂度,通常希望分段数量尽量少。为此,以分段数量最少为目标可建立如下的优化指标:

J2=N

综合上述分析,可将中制导弹道优化问题转化为如下的多目标优化问题:

min{J1,J2}

(9)

式中:J2=N,表示分段数量;J1按照式(4)给出,反映优化性能指标。

对于式(9)的多目标优化问题,2个优化指标之间是相互冲突的,一方面为了使得指标J1尽量小,要求分段数量尽量多,即J2尽量大;但另一方面按照分段数量指标要求,又希望J2尽量小,这实际上与J1对J2的要求是矛盾的。综合上述分析,式(9)的求解不一定存在全局最优解,但可存在这样的解,对一个或几个指标函数不可能进一步优化,对其它指标函数不至于劣化,即非劣最优解[11]。基于此,本文研究中利用指标函数J1对指标函数J2中的分段数量具有很强依赖性,而在特定分段数量下指标函数J2可独立于计算的特点,将上述优化问题转化为在给定分段数量J2的情况下分段参数与指标参数的分层优化问题,进而可将该优化问题转化为如下的双层优化问题:

minJ2=N

s.t.N≥2,N为整数

kx|x(tf)-xf|]

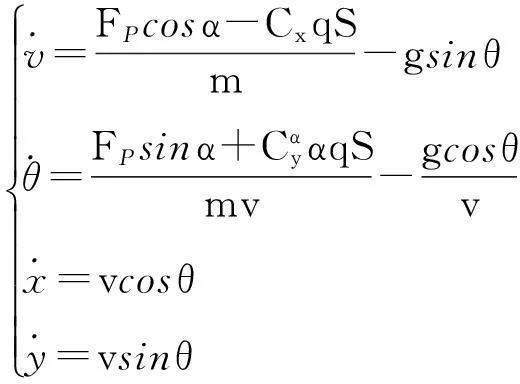
αmin≤α≤αmax

qmin≤q≤qmax

|n|≤nmax

(10)

在对上述双层优化问题进行求解时,本文研究采用微粒群方法进行分层优化求解,结合指标函数J1与J2的相互依赖性关系。首先,选定上层指标函数J2的非最优N;然后,将此非最优解N代入到下层,对指标函数J1进行寻优,获得下层优化解;当下层指标函数无法满足阈值时,对N进行调整并重新对指标函数J1进行寻优。如此循环,直到满足阈值为止。基于以上思路,可设计具体求解方法:第1层,采用n个不同的微粒群种群搜索N个分段数量,每一种分段数量代表一个可唯一标识的种群;第2层,以上层结果为初始条件,在各种群内采用l个微粒各自对应的控制参数进行优化。其基本原理如图1所示。

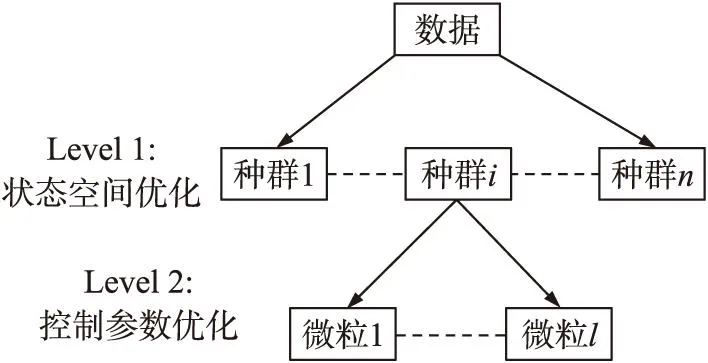
图1　分层优化原理图

具体求解方法可采用文献[12]中的双层优化方法进行,这里不再赘述。

3仿真算例

为验证本文算法的有效性,以某拦截器为对象,对如下的中制导弹道优化问题进行研究。以末速度最大为优化指标进行弹道优化设计,选择优化因子时认为末速度最大与达到终端优化条件同等重要,优化过程中选择优化条件和指标如表1所示。

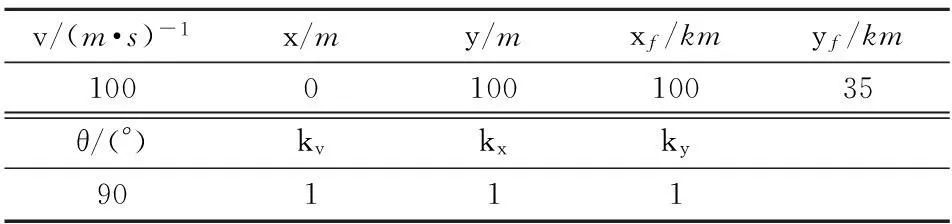
表1　优化条件

以末速度最大为性能指标的优化结果如图2和表2、表3所示。其中,图2为弹道优化结果,反映了在优化过程中随着各种条件的不同相关变量的变化过程;表2为基于控制量优化结果得到的优化弹道相关弹道结果;表3为控制量优化结果。

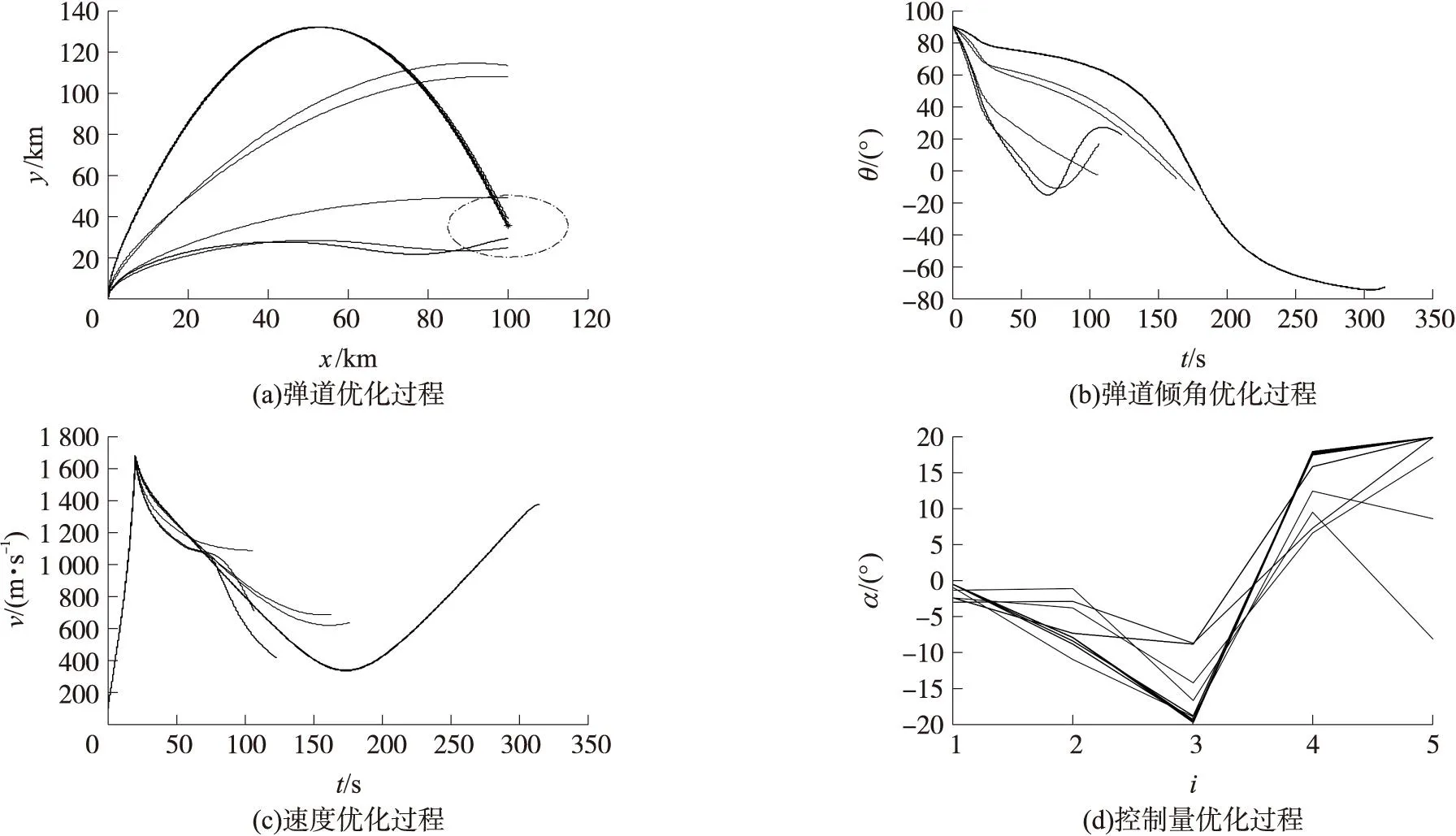
图2　末速最大弹道优化结果

从表2的仿真结果可以看出,优化后的弹道能够满足中制导末端条件,位置偏差很小。从图2的仿真结果可以看出,在不限制拦截器飞行时间时,末速度最大的弹道实质就是一种高抛弹道,其主要原因是拦截器以很短的时间穿越稠密大气层,可以降低拦截器在稠密大气层中飞行受到空气阻力而导致的能量损失,这与拦截器在目标上方飞行以节省能量的思想也是一致的。

表2　末速最大弹道优化结果

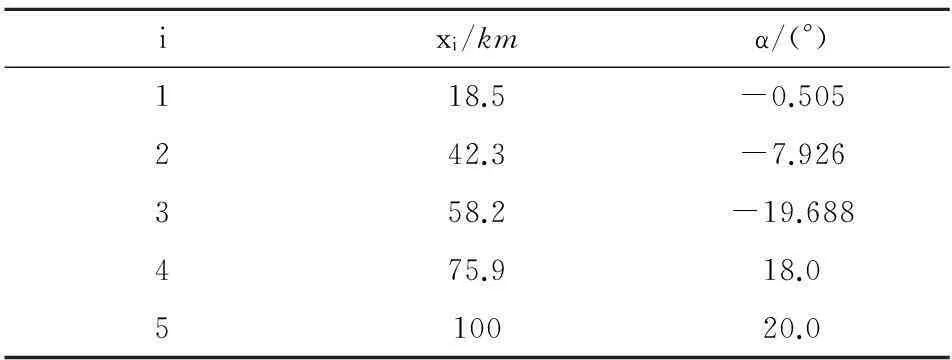
表3　控制量优化结果

4结论

本文针对中制导弹道优化问题,采用微粒群优化算法进行中制导拦截器优化设计。以中制导末端条件为约束,借鉴多重打靶算法思想,将中制导弹道优化问题转化为多目标优化问题;结合指标函数之间的依赖关系,采用微粒群算法对该问题进行分层求解。该方法的设计为弹道优化设计提供了一种可行方法,尽管在论文研究与验证中仅考虑了速度以及位置因素,但该方法同时也适用于其它更多约束的情况,结合对具体弹道特性的分析,可借鉴该方法对弹道设计进行更深入的研究。

参考文献

[1]刘恒军,姜欢,陈万春.防空导弹动能杀伤多层弹道优化MDO算法应用.北京航空航天大学学报,2010,32(2):145-149.

LIU Heng-jun,JIANG Huan,CHEN Wan-chun.Application of MDO algorithm to multi-tier trajectory optimization design for a surface-to-air missile kinetic kill.Journal of Beijing University of Aeronautics and Astronautics,2010,32(2):145-149.(in Chinese)

[2]PHILLIPS C A,DRAKE J C.Trajectory optimization for a missile using a muhitier approach.Journal of Spacecraft and Rockets,2000,37(5):653-662.

[3]陈功,傅瑜,郭继峰.飞行器轨迹优化方法综述.飞行力学,2011,29(4):1-5.

CHEN Gong,FU Yu,GUO Ji-feng.Survey of aircraft trajectory optimization methods.Flight Dynamics,2011,29(4):1-5.(in Chinese)

[4]ANHTUAN D N.A fuel-optimal trajectory for a constrained hypersonic vehicle using a direct transcription method//2004 IEEE Aerospace Conference Proceedings.Piscataway,NJ:IEEE,2004:2 704-2 709.

[5]PETER F G,KLAUS H W.Trajectory optimization using a combination of direct multiples hooting and collocation.AIAA2001-2047.2001.

[6]李佳峰,陈万春.防空导弹最优弹道的协态估计优化算法.北京航空航天大学学报,2009,35(10):1 179-1 183.

LI Jia-feng,CHEN Wan-chun.Co-state estimation algorithm of the surface-to-air missile optimal trajectory.Journal of Beijing University of Aeronautics and Astronautics,2009,35(10):1 179-1 183.(in Chinese)

[7]李瑜,魏毅寅,崔乃刚.洲际助推-滑翔导弹弹道优化与分析.弹道学报,2010,22(2):52-56.

LI Yu,WEI Yi-yin,CUI Nai-gang.Trajectory optimization and analysis for intercontinental boost-glide missile.Journal of Ballistics,2010,22(2):52-56.(in Chinese)

[8]侯明.求解一类最佳轨迹问题的直接多重打靶算法[D ].西安:西北工业大学,1987.

HOU Ming.Resolve for the optimal trajectories based on the direct multiple shooting algorithm.Xi’an:Northwestern Polytechnical University,1987.(in Chinese)

[9]胡朝江,陈士橹.改进直接多重打靶算法及其应用.飞行力学,2004,22(1):14-17.

HU Chao-jiang,CHEN Shi-lu.An improved multiple shooting algorithm for direction solution of optimal control problem and its application.Flight Dynamics,2004,22(1):14-17.(in Chinese)

[10] BERGH F,ENGELBRECHT A P.A new locally convergent particle swarm optimization//Proceedings of IEEE on System,Man and Cybernetics.Piscataway,NJ:IEEE,2002:625-631.

[11] LU H M,YEN G G.Rank-density-based multi-objective genetic algorithm and bench mark test function study.IEEE Transactions on Evolutionary Computation,2003,7(4):325-342.

[12] 邵雷,雷虎民,赵宗宝.基于双层优化的非线性系统多模型建模方法研究.计算机应用,2009,29(5):1 261-1 263.

SHAO Lei,LEI Hu-min,ZHAO Zong-bao.Bilevel optimization based multi-model modeling method for nonlinear systems.Journal of Computer Applications,2009,29(5):1 261-1 263.(in Chinese)