多雷达含缺损信息外弹道解算方法研究

多雷达含缺损信息外弹道解算方法研究

姜大治,王不了,杨军

(92941部队,辽宁 葫芦岛 125000)

摘要:为解决雷达测量信息受地、海杂波的强烈干扰,导致雷达俯仰角测量难以构成有效闭环,目标俯仰角信息超差严重,并通过坐标系变换,向目标各维坐标传导超差信息的问题,该文综合考虑地、海杂波对方位角和斜距信息影响较小,以及海上靶场雷达测量网的布站特点,提出了一种利用多台雷达共有段落的方位角和斜距信息,构建联合处理模型,解算目标弹道的方法。数据测试证明,该方法可以有效解决雷达部分测量信息超差问题,提高靶场雷达测量数据处理的精度和可靠性。

关键词:雷达测量;杂波干扰;数据处理;外弹道

收稿日期:2013-11-13

作者简介:姜大治(1977- ),男,工程师,硕士,研究方向为外测数据建模与处理。E-mail:jdzandwy@sina.com。

中图分类号:TN959.6文献标识码:A

ResearchonAlgorithmforMultiradarTrajectoriesWithDefectInformation

JIANGDa-zhi,WANGBu-liao,YANGJun

(Unit92941ofPLA,Huludao125000,China)

Abstract:The radar measurement is interfered by the clutter of earth and sea,and the measurement of pitch angle is difficult to form an effective closed-loop,and the pitch angle information seriously exceeds the error tolerance,and transmits the error to every coordinates of the target through coordinate transformation.Aiming at this problem,the features of the radar distribution of sea range and the earth were taken into account,as well as the problem that the sea clutter information has less affect on azimuth and slope,and a combined processing model and algorithm were presented based on the common section of azimuth and slope information of multiradar.Test data show that this method can effectively solve the radar partial measurement information error tolerance problems and improve the precision and reliability of data processing of the measurement in sea range.

Keywords:radarmeasurement;clutter;dataprocessing;exteriortrajectory

随着微电子和计算机技术的高速发展,测量雷达在目标识别、抗干扰、过捷处理和高精度测量等方面都有较快发展,技术性能不断提高[1-3]。但是对于海上靶场陆海结合的复杂试验环境,如何完成对低空、大射程、小型化、高动态的导弹类目标的测量,对靶场雷达测量网是一个巨大挑战。为保证靶场雷达网的测量精度和可靠性,一般会在沿岸高点布设多部雷达。地形、杂波、遮挡和多路径等多种因素的干扰,以及测量雷达自身的开环跟踪模式,导致雷达俯仰角测量信息超差严重[5-7]。并且在雷达测量坐标系向目标发射坐标系或假定坐标系转换过程中,大量误差被传递到测量目标各维坐标中,使目标三维坐标均受到雷达俯仰角超差信息的影响。为克服雷达单个超差信息源对整体数据的影响,本文提出了一种利用多台雷达共有段落的方位角和斜距信息,构建联合目标外弹道解算模型以解算目标轨迹的方法。数据测试结果证明了本文方法的正确性和有效性。

1方法模型

1.1　双雷达定位

当待测目标被2台雷达同时捕获时,可使用一台雷达的方位、斜距信息和另一台雷达的斜距信息完成定位解算。以其中一台雷达基准点为坐标原点建立基准坐标系,完成各雷达时间和空间的统一。设基准雷达测量值为(Ai,Ei,Ri),辅助雷达测量值为(Ahi,Ehi,Rhi),辅助雷达基准点坐标为(xh,yh,zh),待测目标坐标为(xti,yti,zti),其中,i表示数据序列,i=1,2,…;(A,E,R)为雷达测量坐标系下的球坐标值,其中,A为方向角,E为俯仰角,R为斜距;(x,y,z)为所定义直角坐标系下的三维坐标值;下标t表示采样时刻。以下含义相同。

建立方程如下:

(1)

tanAi=-zti/xti

(2)

由式(1)可得:

xhxti+yhyti+zhzti=H

(3)

其中:

由式(1)～式(3)可得:

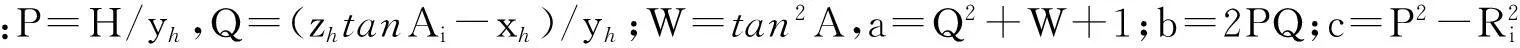
由于xti值存在2种可能,因此,需进行判断。设雷达测量坐标系下雷达测量值为(Aci,Eci,Rci),待测目标坐标为(xci,yci,zci)。则对雷达测量网中任一雷达有如下关系成立:

xci=RcicosEcicosAcii=1,2,…,n

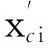
1.2　多雷达定位

当待测目标被2台以上雷达同时捕获时,由于斜距信息受测量环境干扰较小,且随测量目标距离增加精度下降较小,因此可使用多R定位模式完成目标位置解算。设目标定位解算结果矩阵为V,将雷达网多R定位方程写为矩阵形式:

V=GΔX-L

(4)

设目标位置的初始值为(x0,y0,z0),雷达站址坐标为(xj,yj,zj),其中j表示雷达序号,j=1,2,…,nR,nR表示有效跟踪目标的雷达数量。当nR≥3时,计算目标位置修正值:

ΔX=(GTG)-1GTL

(5)

式中:

ΔX=(ΔxΔyΔz)T,

(Δx,Δy,Δz)为目标位置坐标的修正值。

则目标的新位置坐标为

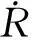
(6)

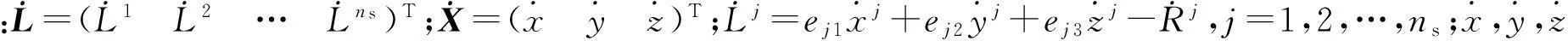
2精度分析

以3台雷达定位为例,设各雷达站雷达天线中心坐标为(xj,yj,zj),j=1,2,3,所测目标坐标为(xti,yti,zti)。对于各测量雷达均有:

(7)

式中:Ri表示t时刻目标与第i个雷达站之间的距离。式(7)可表示为

xti=f(xj,yj,zj,Ri)

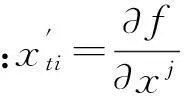
将式(7)两边对xj求导,得:

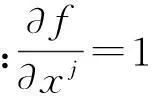
同理可求出:

当xi(i=1,2,…)彼此独立时,对于一般性函数y=f(x1,x2,x3,…,xi),其不确定度传递公式为

(8)

将计算结果代入到式(8)中可得:

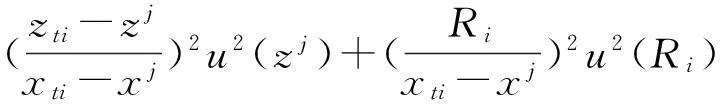
其中:U(xti),u(xj),u(yj),u(zj),u(Ri)分别为xti,xj,yj,zj,Ri的不确定度。同理可求出:

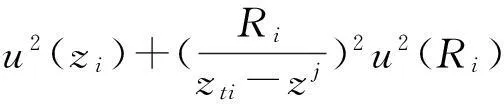
为讨论方便,做以下假设:①雷达为同型测量雷达;②测量不受地球曲率影响;③电磁波传播不受大气层影响;④测量误差服从正态分布。依据假设可得:

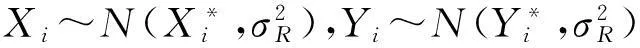
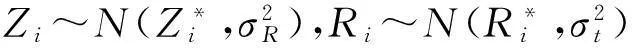
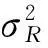
因此可知,距离误差和雷达站址坐标误差对定位结果的影响程度与各自的方差大小及对应的坐标方向余弦有关,方差越大,影响程度就越大。因此,通过增加雷达网测量雷达数量可提高定位结果精度;当雷达数量一定时,可通过合理布站降低误差因子,提高雷达网测量精度。此外,应尽量使雷达远离强辐射区域,并将雷达布置在沿岸高点,以减少环境和地形带来的影响。

3算法流程

①收集各雷达测量数据和相关信息;

②完成数据有效性判定和野点剔除等处理;

③完成共有段落统计及雷达同步采样处理;

④依据锁定目标雷达数量,确定计算模型;

⑤依据外弹道解算模型完成单雷达或多雷达定位;

⑥如果有3台以上雷达包含斜距变化率信息,依据式(6)计算目标速度,否则微分求速;

⑦比较多雷达计算结果和各雷达单站解算结果,分析结果正确性;

⑧综合全部信息,形成目标完整轨迹。

算法流程如图1所示。

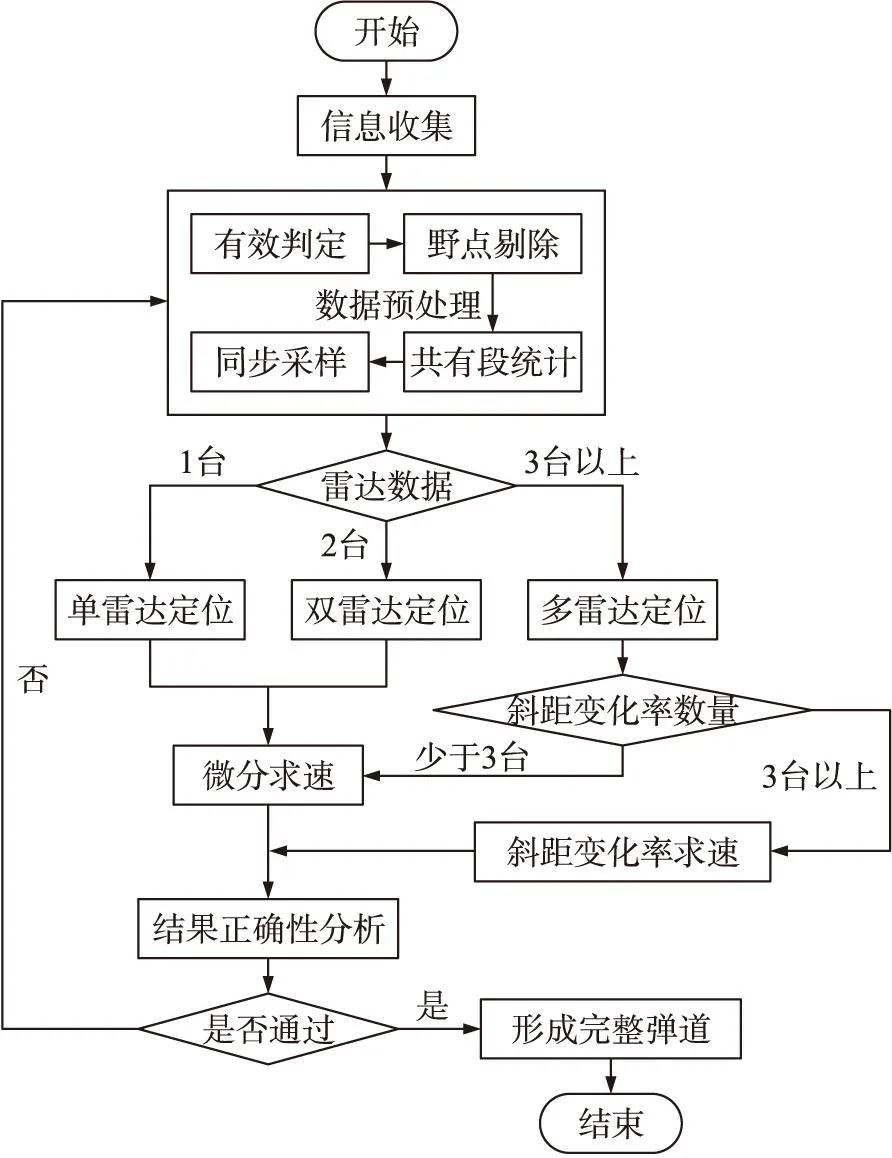
图1　程序流程图

4测试与分析

以某民用飞行器测量结果为例,忽略测量部位不一致误差,以飞行器搭载的GNSS接收机(双频、20 Hz)记录信息相位差分结果作为真值数据。共有5台雷达参与测量,其中4台记录有斜距变化率信息,测量距离为60～130 km,选取全部雷达正常跟踪段落作为测试数据,目标位置和速度解算结果(假定坐标系)误差统计情况如表1所示。

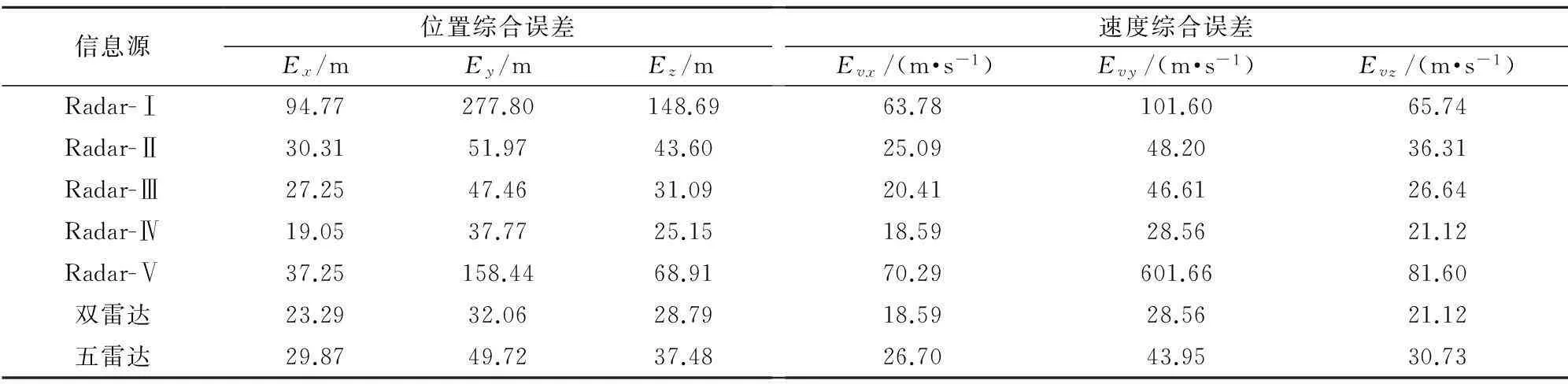
表1　数据统计与分析

双雷达联合定位选取Radar-Ⅱ和Radar-Ⅳ,采用式(3)完成定位,交会角度为60°～105°;五雷达定位采用多R定位;与其它雷达装备相比Radar-Ⅰ和Radar-Ⅴ有更多测量时间是在低仰角(俯仰角测量值小于3°)条件下完成的。分析可知,2种多雷达定位模式均避免了超差俯仰角数据对最终结果的影响。由于交会角度较好,并且未采样超差较为严重的雷达装备,因此,采用双雷达定位改善效果更为明显。由于Radar-Ⅰ和Radar-Ⅴ的斜距信息中含有较大误差,导致五雷达最终定位结果误差偏大。综上可知,使用本文提出的多雷达联合定位方法完成目标位置和速度解算,结果正确,位置和速度精度均得到提高。精度提高幅度与俯仰角测量误差和斜距大小,以及雷达布站位置和目标特性等因素有关。实际目标测试证明了本文提出方法的正确性。

5结束语

本文从试验实际需求出发,综合利用靶场雷测网信息资源,研制了多雷达定位模型,克服了俯仰角超差对最终位置结果的影响。因为雷达测距原理相对简单,信息可靠性强,因此,使用多R定位模型可提高结果的可靠性,并在一定程上提高定位结果精度。由于各雷达跟踪目标的部位不一致,因此直接使用本文方法可能会出现模型不收敛现象,而导致弹道解算失败。多雷达定位精度同样受雷达和目标几何分布影响,当双雷达定位交会角趋于0°或180°,或多斜距定位误差因子过大时,均会导致模型发散。因此,实际应用中应尽可能修复雷达测量部位不一致误差,并择优选取布站位置符合要求的雷达进行目标外弹道解算。

参考文献

[1]常清,潘江怀,安瑾.多雷达距离测量空间定位方法及精度分析.电光与控制,2012,19(6):45-47.

CHANGQing,PANJiang-huai,ANJin.Locatingalgorithmandaccuracyanalysisformulti-radarrangedetecting.ElectronicsOptics&Control,2012,19(6):45-47.(inChinese)

[2]HERMANSM,POOREAB.Nonlinearleast-squaresestimationforradarandnavigationbiases.SPIE,2006,6236:1 701-1 717.

[3]OKELLONN,RISTICB.Maximumlikelihoodregistrationformultipledissimilarradars.IEEETransactionsonAerospaceandElectronicSystems,2003,39(3):1 074-1 083.

[4]胡涛.巡航导弹的发展趋势.飞航导弹,2002(6):5-8.

HUTao.Thedevelopmenttrendofcruisemissile.CruiseMissile,2002(6):5-8.(inChinese)

[5]张雅斌.高频地波雷达干扰与海杂波信号处理研究.西安:西安电子科技大学,2010:105-108.

ZHANGYa-bin.StudyonsignalprocessingofinterferenceandseaclutterforHFsurfacewaveradar.Xi’an:XidianUniversity,2010:105-108.(inChinese)

[6]GRECOM,BORDONIF,GINIF.X-bandsea-clutternonstationarity:influenceoflongwaves.IEEEJournalofOceanicEngineering,2004,29(2):269-282.

[7]WHITEWD.Low-angleradartrackinginthepresenceofmultipath.IEEETransactionsonAerospaceElectronicSystems,1974,10:835-853.

[8]姜大治,杨军.利用GPS精密差分信息实现舰船类目标关键部位间接测量.全球定位系统,2012,37(3):22-25.

JIANGDa-zhi,YANGJun.UsingGPSprecisiondifferenceinformationtorealizeshiptargetskeypartindirectmeasurement.GNSSWorldofChina,2012,37(3):22-25.(inChinese)