混合坐标系下跟踪自由段弹道导弹的IMM-UPF 算法研究

混合坐标系下跟踪自由段弹道导弹的IMM-UPF算法研究

郭跃1,刘新学1,王才红2

(1.第二炮兵工程大学 初级指挥学院,西安 710025;2.第二炮兵装备研究院,北京 100089)

摘要:为了提高对自由段弹道导弹的跟踪精度,在混合坐标系下构建了自由段弹道导弹不做机动时更为准确的系统动力学模型。为提高对自由段弹道导弹目标机动时的适应能力,结合Singer和当前统计模型给出了自由段弹道导弹机动时的系统动力学模型,利用交互多模型(IMM)实现了对导弹的跟踪。在对探测数据的处理过程中,为了避免探测数据中闪烁噪声的影响,提出了IMM-UPF算法,并分别与EKF、UKF、UPF等算法做了对比分析。仿真结果表明,IMM-UPF算法对存在机动的自由段弹道目标以及雷达闪烁噪声具有良好的适应性,较EKF、UKF、UPF能够获得较高的跟踪精度。

关键词:混合坐标系;弹道导弹;自由飞行弹道;交互多模型;不敏粒子滤波

收稿日期:2014-03-19

作者简介:郭跃(1986- ),男,博士研究生,研究方向为飞行动力学与制导理论。E-mail:guoyue240@163.com。

中图分类号:V412.1文献标识码:A

A Study on IMM-UPF of Tracking Ballistic Missile at Free-flight

Phase in Mixed Coordinate System

GUO Yue1,LIU Xin-xue1,WANG Cai-hong2

(1.Primary Command College,Second Artillery Engineering University,Xi’an 710025,China;

2.Second Artillery Equipment Research Institute,Beijing 100089,China)

Abstract:To improve the accuracy of tracking ballistic missile at free-flight phase,the accurate model of non-maneuvering ballistic missile at free-flight phase was constructed in mixed coordinate system.To improve the adaptability to maneuvering ballistic target,the system dynamics model of ballistic missile maneuvering at free-flight phase was presented combined with Singer and current statistical model,and the interaction multi-models(IMM)was used to track the missile.To avoid the effect of the flicker noise in the tracking data,the IMM-UPF algorithm was proposed,and it was compared to EKF,UKF and UPF respectively.The simulation results show that the IMM-UPF has better adaptability to the maneuvering ballistic target and the flicker noise of target’s data,and it has high accurate tracking ability than EKF,UKF and UPF.

Key words:mixed coordinates system;ballistic missile;free-flight trajectory;interacting multiple model;unscented particle filter

弹道导弹在自由段飞行过程中一般只受到重力和机动控制力的作用而且飞行时间长,因此,自由飞行段是反导拦截的最佳时机,研究雷达系统对自由段弹道目标的跟踪滤波算法对于自由段目标的准确跟踪和拦截都有着重要意义。对自由段弹道目标的运动模型的准确建模和对雷达探测时滤波算法使用是提高其探测精度的关键。文献[1-2]对弹道导弹自由段的运动模型以及一些基本的跟踪模型进行了论述,但是跟踪坐标系通常建立在笛卡尔坐标系或传感器坐标系下。若在笛卡尔坐标系下建立目标状态方程,当把传感器坐标下的非线性量测值直接转换为笛卡尔坐标系下的量测值时会导致偏差,同时转换后的量测噪声会变成非高斯的、状态依赖的噪声,从而导致滤波困难。在传感器坐标系下建立量测方程可以使得量测方程线性、非耦合且噪声服从高斯分布,但是系统动力学方程高度非线性和耦合复杂。因此本文选择混合坐标作为跟踪坐标系。混合坐标系是指在笛卡尔坐标系下建立系统状态方程,并对目标运动参数进行预测,然后将预测的状态和协方差矩阵转到量测坐标系进行传感器坐标系的状态更新,最后将传感器坐标的更新结果转移到笛卡尔坐标系[3-5]。本文在原有的自由段运动模型的基础上结合Singer模型和当前统计模型给出了滤波算法的系统动力学方程,并通过交互多模型(IMM)对目标的不同状态进行准确跟踪[6-9]。同时将IMM和不敏粒子滤波(UPF)组合提出IMM-UPF算法[10-11],并在混合坐标系下构建了自由段弹道目标的跟踪模型,这样既便于对存在机动的自由段弹道目标进行准确跟踪,也可以克服雷达系统存在闪烁噪声等非高斯噪声的不良影响。

1雷达坐标系内导弹目标的动力学模型

本文的混合坐标系在东北天(ENU)坐标系下建立目标的状态方程,在球坐标系下建立目标的量测方程。设雷达参考坐标系(radar reference coordinates,RRC)的坐标原点为Or;OrXr,OrYr是地球参考椭球的切线,分别指向东和北;OrZr垂直于当地水平面,即为东北天(ENU)坐标系。设雷达站球坐标系原点Or的大地纬度、大地经度、大地高程分别为Br0,Lr0,Hr0;选择地球模型为标准椭球体,则雷达站Or的大地直角坐标系的坐标rre0=(xre0yre0zre0)T的各参量为

(1)

式中:a为参考椭球体的长半轴,e为地球扁率。考虑地球自转,设ω为地球自转角速度,则地心惯性直角坐标系(ECI)到雷达坐标系(ENU)的转换矩阵为

(2)

(3)

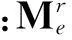
对式(3)求导有:

(4)

二阶求导有:

(5)

其中,

同理:

(6)

求一阶导数有:

(7)

采用平方反比的重力模型,有[1,2]:

(8)

(9)

进一步化简有:

(10)

ω2Φ2,

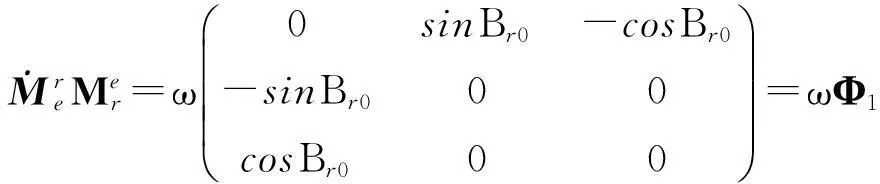
-ω2Φ2。

综合化简,得:

(11)

2基于IMM-UPF算法的机动目标跟踪

(12)

(13)

Xk+1=f(Xk)+Wk

(14)

2.1　基于Singer模型的目标状态方程

由于拦截弹的最大加速度是有限的且具有机动不确定性,就探测方来讲可认为拦截弹的机动时刻是随机的,符合Singer的一阶相关模型。对应的导弹自由段的Singer一阶相关模型为

(15)

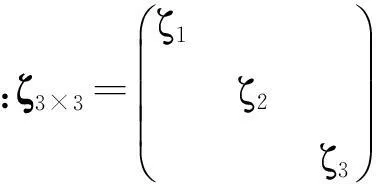
2.2　基于CS模型的目标状态方程

周宏仁认为当目标以某一加速度机动时,下一时刻的加速度是有限的且在当前加速度的邻域内,其机动加速度的当前概率密度用修正的瑞利分布描述。CS模型的本质是非零均值的时间相关模型[12-14]:

(16)

(17)

则对应的导弹自由段的CS模型为

(18)

3IMM-UPF算法的实现

②对各模型相应的粒子进行交互计算。

(19)

③模型匹配粒子滤波器,将

带入j各模型的UPF粒子滤波器,其具体变化为

(20)

(21)

量测更新有

(22)

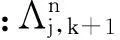
④模型概率更新为

(23)

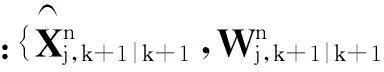
⑥对M个模型的N个粒子进行输出交互,对其求加权的平均和。

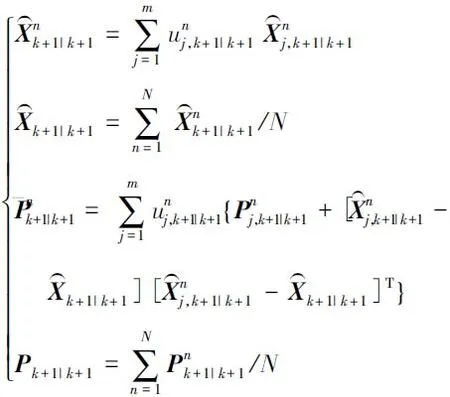
(24)

返回①。

4仿真及结果分析

设目标的观测初测值为(48 833m,53 170m,290m,1 630m/s,1 370m/s,-10m/s),导弹初始的经、纬度和射向角为(118.3°,43.7°,36.9°),雷达的点位为(0m,0m,0m),探测频率为1Hz;qα,qβ分别为目标方位角和俯仰角。雷达探测数据的协方差矩阵为diag(10 000,1×10-8,4×10-8,100,1×10-10,1×10-12),系统的噪声的协方差矩阵为diag(1×104,2.5×103,2.5×103,4×102,2.25×102,2.25×102),分别采用EKF、UKF和IMM-UPF方法对目标进行跟踪,以均方根误差(RMSE)作为评估指标,蒙特卡洛仿真100次,EKF、UKF、IMM-UPF的RMSE分析比较如表1所示,表中Rx,Ry,Rz,Rvx,Rvy,Rvz分别为各参量的均方根误差。

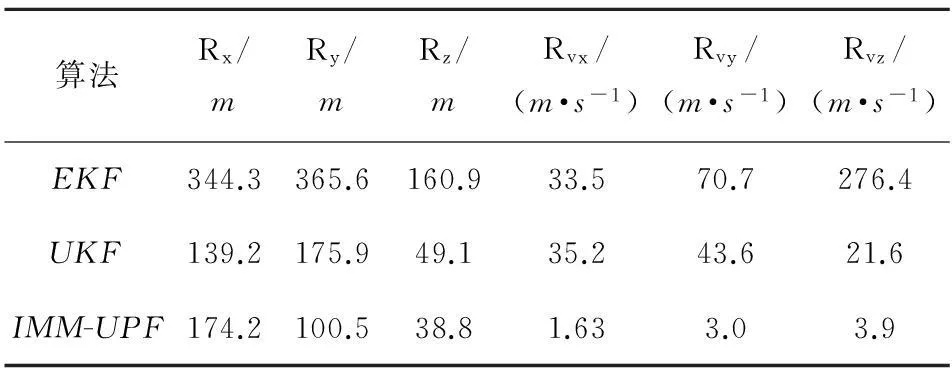
表1　3种算法的 RMSE比较分析

EKF和UKF对闪烁噪声适应性差,因此这里重点对UPF和IMM-UPF算法进行分析。构造雷达闪烁噪声为[16]ray_noise=ε*gauss_noise1+(1-ε)*gauss_noise2,其中令ε=0.3;gauss_noise1的均值为(100m,1×10-4rad,2×10-4rad,10m/s,1×10-5rad/s,2×10-5rad/s),标准差为(10m,2×10-5rad,1×10-5rad,1m/s,1×10-6rad/s,2×10-6rad/s);gauss_noise2的均值为(200m,1×10-4rad,2×10-4rad,10m/s,1×10-5rad/s,2×10-5rad/s),标准差为(10m,2×10-5rad,1×10-5rad,2m/s,1×10-6rad/s,2×10-6rad/s)。系统噪声同前,UPF、IMM-UPF的RMSE的分析比较如表2所示。

表2　 UPF与 IMM- UPF算法的 RMSE比较分析

对存在白噪声干扰的雷达探测数据使用EKF、UKF和UPF进行滤波比较分析,结果如图1所示。从图中可以看出UPF对探测数据有更好的处理能力,对速度跟踪有着尤其好的跟踪效果,而EKF和UKF存在不同程度的发散。对存在闪烁噪声的探测数据的处理结果见图2。由图2可见,IMM-UPF与UPF相比,随着时间的累积UPF的滤波误差会逐渐累积甚至导致分散,而IMM-UPF则能避免误差的累积和滤波的发散。从仿真结果来看本文构建的滤波模型是准确的,可对自由段的弹道目标实现准确跟踪,对存在白噪声和闪烁噪声的雷达均有良好的适应性。

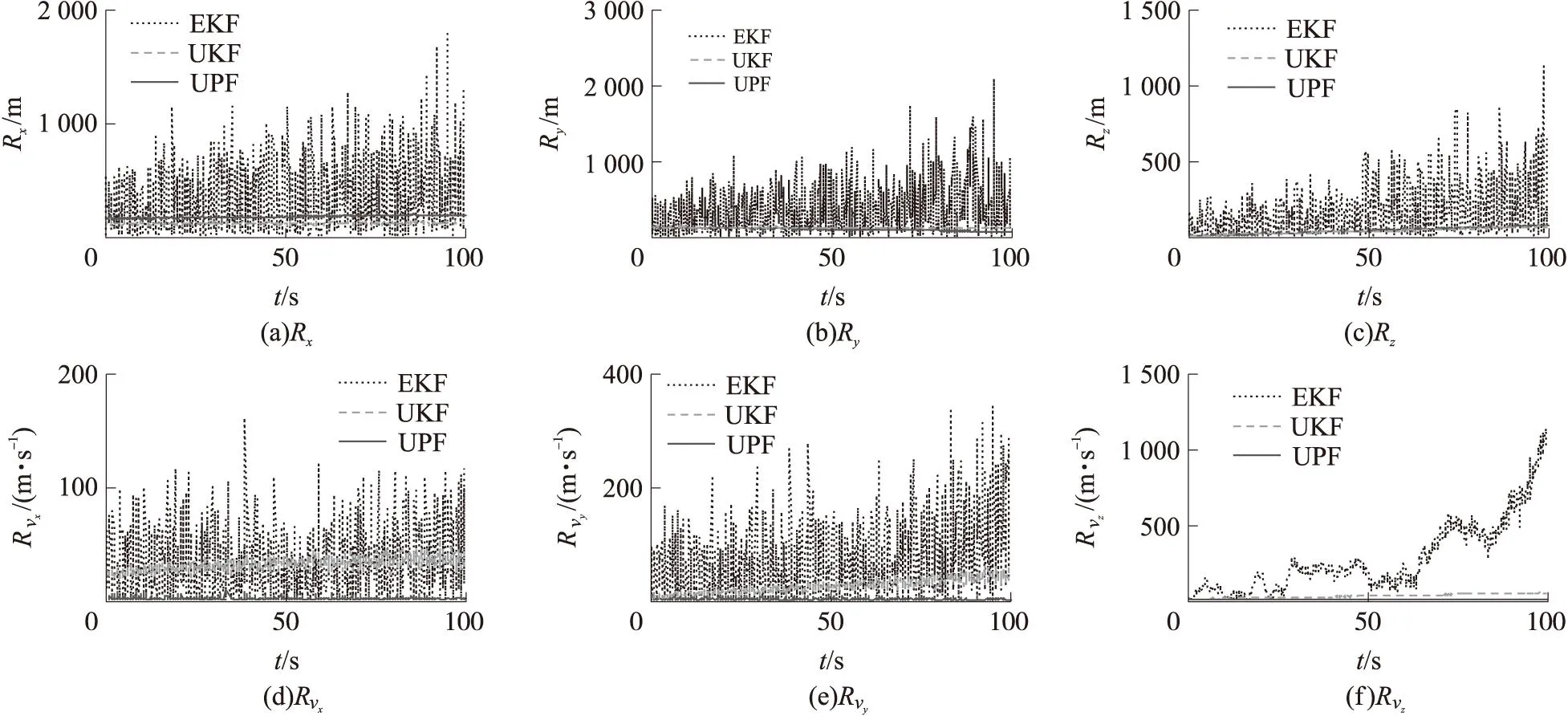
图1　3种算法的位置和速度RMSE分析比较

图2　UPF与IMM-UPF的位置和速度RMSE分析比较

5结论

IMM-UPF算法对存在闪烁噪声的机动目标有着较好的跟踪效果,无论在位置和速度跟踪方面都较UKF和UPF有着更好的跟踪精度。UPF算法对存在白噪声的机动目标有着较好的跟踪效果,但对存在闪烁噪声的目标进行跟踪时容易造成误差的累积。EKF对机动目标的跟踪引起的发散较为严重,UKF的精度介于EKF和UPF之间,跟踪速度较快,但不适合对存在闪烁噪声的数据进行滤波。但是IMM-UPF相对EKF和UKF而言计算量较大,模型复杂而且模型准确性也较为敏感。

参考文献

[1]张毅,杨辉耀,李俊莉.弹道导弹弹道学.长沙:国防科技大学出版社,1999:111-157.

ZHANG Yi,YANG Hui-yao,LI Jun-li.The ballistic trajectory.Changsha:National University of Defense Technology Press,1999:111-157.(in Chinese)

[2]LI X R,JILKOV V P.A survey of maneuvering target tracking,part Ⅱ:ballistic target models.SPIE,2001,4 473:1-23.

[3]秦永元,张洪钺,王叔华.卡尔曼滤波与组合导航原理.西安:西北工业大学出版社,2004:69-138.

QIN Yong-yuan,,ZHANG Hong-yue,WANG Shu-hua.Kalman filter and the principle of combined guidance.Xi’an:Northwestern Polytechnical University Press,2004:69-138.(in Chinese)

[4]JULIERSJ,UHLMANNJK.Unscentedfilteringandnonlinearestimation.ProceedingsofIEEE,2004:92(3):401-412.

[5]GREWALMS,ANDREWSAP.Kalmanfiltering,theoryandpracticeusingMATLAB.NewYork:WileyInterscience,2001:56-104.

[6]WUY,HUD,WUM,etal.UnscentedKalmanfilteringforadditivenoisecase:augmentedversusnon-augmented.IEEESignalProcessingLetters,2012:12(5):357-360.

[7]JOUNIH,SIMOS.OptimalfilteringwithKalmanfiltersandsmoothers:amanualforMatlabtoolboxEKF/UKF.Finland:HelsinkiUniversityofTechnology,2007:20-34.

[8]EASTHOPEPF,HEYSNW.Multiple-modelorientedtarget-trackingsystem.SPIE,1994,2 235:72-79.

[9]LAWTONJA,JESIONOWSKIRJ,ZARCHANP.Comparisonoffourfilteringoptionsforaradartrackingproblem.AIAAJournalofGuidance,ControlandDynamics,1998,21(4):618-623.

[10]FARINAA,RISTICB,BENVENUTID.Trackingaballistictarget:comparisonofseveralnonlinearfilters.IEEETransactionsonAerospaceandElectronicSystems,2002,38(3):854-867.

[11]COSTAPJ.AdaptivemodelarchitectureandextendedKalman-Bucyfilters.IEEETransactionsonAerospaceandElectronicSystems,1994,30(2):525-533.

[12]DEMPSTERRJ,BLACKMANSS,NICHOLSTS.CombiningIMMfilteringandMHTdataassociationformultitargettracking//Proceedingsofthe29thSoutheasternSymposiumonSystemTheory.Cookeville:IEEE,1997:123-127.

[13]CHENR,LIUJS.MixtureKalmanfilters.JournaloftheRoyalStatisticalSociety,2000,52(3):493-508.

[14] 周宏仁,敬忠良,王培德.机动目标跟踪.北京:国防工业出版社,1991:134-153.

ZHOUHong-ren,JINGZhong-liang,WANGPei-de.Mobiletargettracking.Beijing:NationalDefenseIndustryPress,1991:134-153.(inChinese)

[15] 朱志宇.粒子滤波算法及其应用.北京:科学出版社,2010:32-144.

ZHUZhi-yu.Theapplicationofparticlefilteralgorithm.Beijing:SciencePress,2010:32-144.(inChinese)

[16]MARCELOGSB,ANTONP.Improvedparticlefiltersforballistictargettracking.IEEEICASSP,2004,2:705-708.