基于 SNVA 的机动目标状态估计

基于SNVA的机动目标状态估计

乔雪,白亚腾

(中国矿业大学 信息与电气工程学院,江苏 徐州,221116)

摘要:利用位置预测估计值与位置滤波估计值之间的偏差进行加速度方差自适应调节,提出一种基于状态噪声方差自适应(SNVA)的机动目标状态估计方法。采用SNVA对目标加速度噪声方差进行自适应调整,实现了对当前统计模型的改进;利用扩展卡尔曼滤波算法对目标状态进行估计。仿真结果表明,基于SNVA的扩展卡尔曼滤波算法对机动目标速度估计的绝对误差小于0.1 m/s,加速度估计的绝对误差小于0.1 m/s2,能够对机动目标的状态进行准确的估计。

关键词:机动目标;当前统计模型;扩展卡尔曼滤波;状态估计

收稿日期:2014-02-24

基金项目:教育部博士学科点专项科研

作者简介:乔雪(1990- ),女,硕士研究生,研究方向为复杂系统分析与控制。E-mail:1219771581@qq.com。

中图分类号:TJ765.4文献标识码:A

ManeuveringTargetStateEstimationBasedonSNVA

QIAOXue,BAIYa-teng

(SchoolofInformationandElectricalEngineering,ChinaUniversityofMining&Technology,Xuzhou221116,China)

Abstract:By using the difference between the location forecast estimation and the corrected location estimation,the acceleration variance was adjusted adaptively.A maneuvering target state estimation method based on state noise variance adaptive(SNVA)was proposed.The SNVA was used to adaptively adjust the system noise variance in target state estimation system,which can improve the current statistical model.The extended Kalman filter algorithm was used to estimate the target state.Simulation results show that the extended Kalman filter algorithm based on SNVA can estimate the target state accurately.The absolute estimation error of velocity is less than 0.1 m/s,and the absolute estimation error of acceleration is less than 0.1 m/s2.The target state can be accurately estimated by the proposed method.

Keywords:maneueringtarget;currentstatisticalmodel;extendedKalmanfilter;stateestimation

对于机动目标状态估计问题的研究是目前自动控制领域的热点课题之一。将滤波算法与机动目标模型[1-2]相结合可以对机动目标的状态进行估计。在滤波算法的发展历史中有很多学者提出了不同的滤波算法,其中,卡尔曼滤波理论是由Kalman于1960年提出的。对于线性系统,运用卡尔曼滤波算法可以得到系统状态的最小均方差估计。对发生机动运动的非线性系统通常采用扩展卡尔曼滤波(extendedKalmanfilter,EKF)算法[4-5]。EKF算法首先将非线性状态方程通过泰勒级数展开进行线性化处理,线性化后所得到的滤波算法通常被用于对机动目标的状态进行估计。

在对机动目标的状态进行估计之前,首先应该建立机动目标的模型。周宏仁提出的“当前”统计(currentstatistical,CS)模型本质上是一种时间相关模型,机动目标“当前”加速度的预测值即为均值。“当前”统计模型是目前最常用、效果较好的一类实用模型,但是该模型也存在一些局限性,主要表现在以下2个方面:①滤波估计的快速性和准确性均会受限于预先给出的加速度预测极限值;②如果目标实际机动的状态与估计状态不符,则会造成滤波发散,对机动目标的状态估计结果造成影响。

因此,针对上述局限性①的问题,本文在基于CS模型和EKF算法的机动目标状态估计基础上,提出一种基于状态噪声方差自适应(statenoisevarianceadaptive,SNVA)的机动目标状态估计方法。该方法的基本思想是:通过滤波对机动目标的位置进行估计,并求得位置滤波估计值与预测值之间的偏差,进而可以计算偏差在采样时间内的变化率,用所得的位置偏差变化率对当前时刻的加速度方差进行修正。采用这种方法是为了避免由于对加速度的极限值设定不当而造成估计精度降低的问题。与仿真结果的对比证明了这种方法在对强机动目标的状态进行估计时比传统的EKF滤波算法更加有效。

1基于“当前”统计模型的机动目标状态估计

假设机动目标系统的离散状态空间模型为

X(k)=Φ[X(k-1),k-1]+

Γ[X(k-1),k-1]W(k-1)

(1)

Y(k)=H[X(k),k]+V(k)

(2)

式中:X(k)是n维状态向量;Y(k)是m维观测向量;W(k-1)和V(k)分别是k-1时刻和k时刻的系统噪声向量;Γ[X(k-1),k-1]是n×p维系统噪声输入矩阵;H[X(k),k]是m×n维观测矩阵。

①系统状态一步预测估计方程。

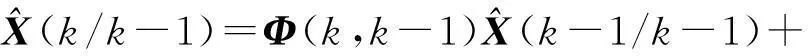
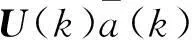
(3)

(4)

Γ(k,k-1)=Γ[X(k-1/k-1),k-1]

(5)

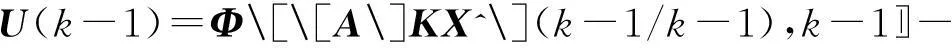
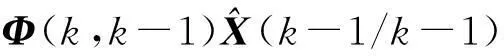
(6)

②一步预测估计误差方程。

P(k|k-1)=Φ(k,k-1)P(k-1/k-1)×

ΦT(k,k-1)+Γ(k,k-1)Q(k)ΓT(k,k-1)

(7)

式中:P(k-1/k-1)是后验估计误差协方差矩阵,Q(k)为系统状态噪声的方差阵,计算公式为

(8)

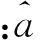
(9)

式中:amax,a-max分别为预先设定的加速度上、下限。

至此,根据式(1)和式(2)以及扩展卡尔曼滤波方程,就可以得到目标的状态估计。图1给出了扩展卡尔曼滤波算法的结构框图,由于系统的量测方程在直角坐标下是非线性的,则应将量测方程中的观测矩阵进行线性化处理:

(10)

图1中,Q(k)为系统状态噪声W(k)的方差,R(k)为观测噪声V(k)的方差,K(k)为卡尔曼滤波增益。

图1　扩展卡尔曼滤波算法的结构框图

在利用扩展卡尔曼滤波进行状态估计的过程中,一方面要求预先给定机动目标加速度的极限值amax和a-max,这个参数不能自适应调节,因此这种状态估计算法的估计能力有限;另一方面,如果缺乏必要的先验信息,机动目标加速度的极限值很难确定,往往与实际系统模型不匹配,因此造成状态估计的精度大大降低。

2状态噪声方差的自适应性

由式(6)可知,在CS模型中状态噪声方差取决于机动目标加速度的极限值amax和a-max。当加速度极限值的取值较大时,较大的噪声方差能够保证对目标机动的快速响应,但是会造成估计精度的降低;当加速度极限值的取值较小时,状态估计精度有所提高,但是系统对机动目标的响应速度较慢。因此,系统不能实时反映目标的真实机动情况。为了扩大基于CS模型的状态估计算法在机动目标状态估计中的应用范围,提高滤波精度,将上述状态估计算法进行改进,提出基于状态噪声方差自适应(state noise variance adaptive,SNVA)的状态估计算法。该算法利用位置观测值和位置滤波估计值之间偏差的变化率对状态噪声方差进行实时调整,从而避免加速度上、下限对滤波估计的影响。

在第k次采样周期T(T是指相邻2次实测之间的时间间隔)内有:

(11)

(12)

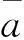
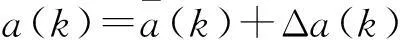
(13)

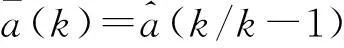
(14)

(15)

(16)

式中:μ是一个正常数。联立式(11)～式(16),可得加速度状态噪声方差:

(17)

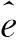
图2　基于SNVA的机动目标状态估计结构图

3仿真研究

3.1　目标机动状态估计

实验主要考察导弹在铅垂面攻击目标的情况,vM,vT分别为导弹和目标的瞬时速率;θ为弹道倾角;θT为目标的高低角;xM,yM和xT,yT分别表示导弹和目标在x和y方向上的位移;比例系数K的取值在10到15之间。导弹与目标在地面坐标系中的位置关系如图3所示,下标d表示地面坐标系。

图3　导弹与目标在地面坐标系中的关系

目标的运动模型为

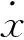
(18)

(19)

比例导引时导弹与目标相对运动的方程组为

(20)

(21)

式中:r为导弹到目标的相对距离,q是目标线方位角,假设地面水平,则θT≈0。设目标是机动的,且存在未知的扰动量ΔθT,ΔvT;将其代入式(18)和式(19),忽略由于ΔθT,ΔvT的存在而引起的Δr,可得到扰动方程组:

(22)

令w1=ΔθT,w2=ΔvT,整理导弹与目标运动方程组,得到系统的状态方程和输出方程:

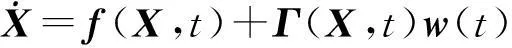
(23)

(24)

式中:

其中:g为重力加速度,ϑ为俯仰角,FP为发动机推力,Fx为迎面阻力,Fy为升力,m为导弹的质量,α为攻角,Mz为俯仰力矩,Jz为导弹绕Ozd轴转动的转动惯量,ωz为导弹绕Ozd轴的旋转角速度。

根据所设计的模型采用Monte Carlo仿真方法进行计算机仿真,取采样次数N=100,得到机动目标沿x轴和y轴方向的速度估计误差均值曲线,如图4和图5所示,图中,Δv表示速度误差,在实验中采样周期T=2 s。

图4　速度误差曲线

由图4可以看出,在100次的采样结果中,x轴方向和y轴方向的速度滤波估计值与真实值之间的误差均小于0.1 m/s。因此可以说明,经过SNVA自适应处理后的机动状态估计方法能够较为准确地反映目标的真实运动状态。

在对目标滤波加速度进行的估计中,通过计算机选取400次的采样结果,结合目标的真实运动加速度求出加速度估计均方根误差σa,并将结果拟合成曲线,如图5所示。σa的具体计算公式如下[10]:

(25)

图5　加速度均方根误差曲线

由图5可以看出,在对目标x方向以及y方向上加速度进行的估计中,滤波后的加速度估计值与目标加速度真实值之间的均方根误差稳定在一个比较小的范围内,说明估计值与真实值之间的偏差较小。因此可以说明,基于SNVA的状态估计算法对机动目标的加速度能够进行比较准确的估计。

综合上述的仿真结果可知,在对2个方向上机动目标运动状态进行的估计中,滤波估计误差都在误差允许的范围内,并没有出现滤波发散现象。由此可以得出以下结论:基于SNVA的机动目标状态估计能够得到目标机动状态的近似无偏估计,并且估计精度高。

3.2　对比仿真

为了进一步验证基于SNVA的状态估计算法在机动目标状态估计中的优势,将SNVA算法和扩展卡尔曼滤波算法同时应用于3.1节的仿真实验中进行对比。在利用扩展卡尔曼滤波对目标状态进行估计时预先设置机动频率为0.001 Hz,加速度的极限值amax=1.0 km/s2和a-max=-0.5 km/s2。实验中得到目标的加速度估计以及加速度估计误差曲线,如图6和图7所示。图中ax和ay分别表示目标在x轴和y轴方向上的加速度瞬时值,N表示采样次数,采样周期T=2 s。

图6　加速度估计曲线

由图6可以看出,在对目标x轴方向和y轴方向上的加速度进行估计的过程中,每次采样的基于SNVA的加速度估计值都比扩展卡尔曼滤波的加速度估计值更加接近真实值。因此可以说明,在机动目标的状态估计问题中,基于SNVA的状态估计算法与扩展卡尔曼滤波算法相比能更加准确快速地对目标状态进行估计。

目标的加速度误差估计曲线如图7所示,图中Δax和Δay分别表示目标在x轴和y轴方向上的加速度误差估计,采样周期T=2 s。

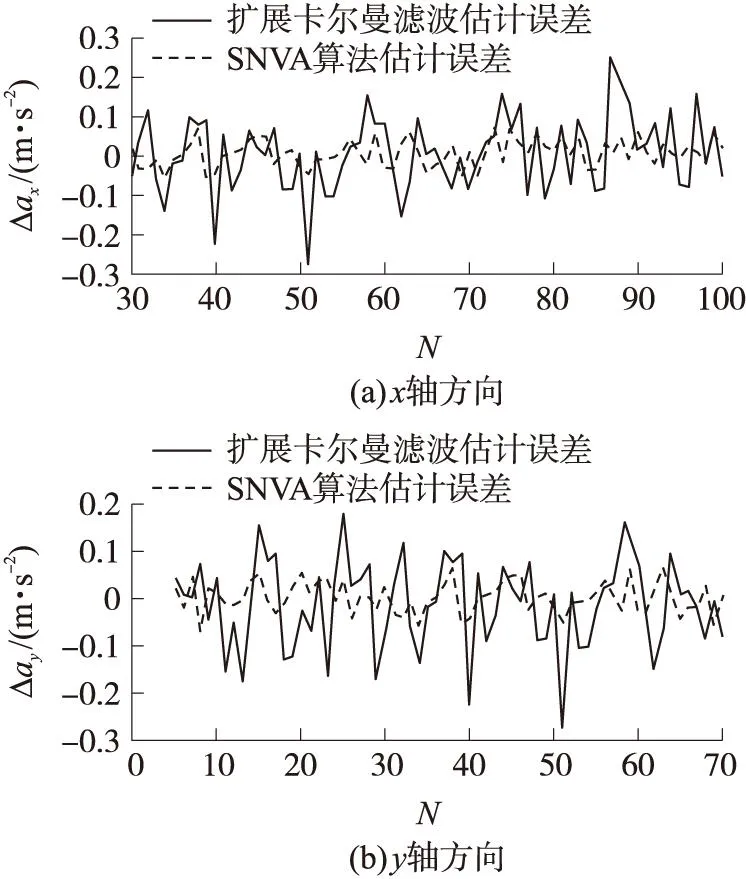
图7　加速度估计误差曲线

由图7可以看出,在对目标的加速度进行估计的过程中,每个采样周期内基于SNVA算法的加速度估计误差都明显小于扩展卡尔曼滤波的估计误差,误差均值在0附近波动,幅值不大,并没有发生滤波发散。由此说明,在机动目标的状态估计问题中,基于SNVA的状态估计算法比扩展卡尔曼滤波更能准确地对目标的状态进行估计。

4结论

本文提出的SNVA算法避免了在机动目标状态估计问题中预先设定的加速度极限值对于状态估计的影响。该方法的特点主要体现在以下2个方面:

①当目标做机动性较强的机动运动时,SNVA可以对目标的状态进行近似无偏估计;

②避免了预先对加速度极限值的设定,能够实时调整加速度极限范围。

因此,在实际工程对跟踪目标的状态估计的应用中,SNVA的实用性较强,估计精度高,跟踪效果很好,并且大大拓宽了对机动目标的机动跟踪范围。

参考文献

[1]兰义华,任浩征,张勇,等.一种基于“当前”模型的改进卡尔曼滤波算法.山东大学学报,2012,42(5):12-17.

LANYi-hua,RENHao-zheng,ZHANGYong,etal.AnimprovedKalmanfilteralgorithmbasedonthe“current”model.JournalofShandongUniversity,2012,42(5):12-17.(inChinese)

[2]LIUJian-shu,LIRen-hou,LIUYun-long.Interactingmultiplemodelalgorithmbasedonthecurrentstatisticalmodel.SystemsEngineeringandElectronics,2008,30(7):1 351-1 354.

[3]WANGJin-hua,CAOJie,WUDi,etal.Anobjecttrackingalgorithmbasedonthe"current"statisticalmodelandthemulti-featurefusion.JournalofSoftware,2012,7(9):2 000-2 008.

[4]常思江,王中原,牛春峰.基于卡尔曼滤波的弹箭飞行状态估计方法.弹道学报,2010,22(3):94-98.

CHANGSi-jiang,WANGZhong-yuan,NIUChun-feng.EstimationapproachofflightstateforguidedprojectilesbasedonKalmanfilter.JournalofBallistics,2010,22(3):94-98.(inChinese)

[5]史金光,刘猛,曹成壮,等.弹道修正落点预报方法研究.弹道学报,2014,26(2):29-33.

SHIJin-guang,LIUMeng,CAOCheng-zhuang,etal.Researchonmethodoffallingpointpredictionfortrajectorycorrectionprojectile.JournalofBallistics,2014,26(2):29-33.(inChinese)

[6]周宏仁,敬忠良.机动目标跟踪.北京:国防工业出版社,1991.

ZHOUHong-ren,JINGZhong-liang.Trackingofmaneuveringtargets.Beijing:NationalDefenceIndustryPress,1991.(inChinese)

[7]王以标,徐毓.基于当前统计模型的改进自适应滤波算法.火力与指挥控制,2010,35(5):86-89.

WANGYi-biao,XUYu.Studyonimprovedadaptivefilteringalgorithmbasedoncurrentstatisticalmodel.FireControl&CommandControl,2010,35(5):86-89.(inChinese)

[8]徐琰珂,梁晓庚,贾晓洪.基于ANFIS的自适应机动目标状态估计算法.系统工程与电子技术,2013,35(2):250-255.

XUYan-ke,LIANGXiao-geng,JIAXiao-hong.AdaptivemaneuveringtargetstateestimationalgorithmbasedonANFIS.SystemsEngineeringandElectronics,2013,35(2):250-255.(inChinese)

[9 ]余跃,刘藻珍.扩展卡尔曼滤波器在导弹制导系统中的应用与仿真//系统仿真技术及其应用学术交流会,合肥:中国科学技术大学出版社,2003:397-400.

YUYue,LIUZao-zhen.SimulationofhomingmissilesystemusingextendedKalmanfilter//AcademicCommunicationSystemSimulationTechnologyanditsApplication.Hefei:PressofUniversityofScienceandTechnologyofChina,2003:397-400.(inChinese)

[10] 杨宏,李亚安,李国辉.一种改进扩展卡尔曼滤波新方法.计算机工程与应用,2010,46(19):18-20.

YANGHong,LIYa-an,LIGuo-hui.AnewmethodofimprovedextendedKalmanfilter.ComputerEngineeringandApplications,2010,46(19):18-20.(inChinese)