初中数学课堂例题教学初探
林朝乐


【关键词】初中数学 课堂例题
教学策略
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2015)12A-
0100-01
例题教学是学生理解、掌握和运用数学概念、法则、性质、定理、方法、思想的必要过程,是学生将数学知识和技能转化为能力的必要途径和手段。有效的例题教学,既能使学生掌握数学基本知识在解决问题中的应用,也能加深对基本知识的领会和理解,更好地掌握解题技巧,促进数学素养的提高。如何设计例题教学,是一个值得我们深思的课题。
一、切中要害举例,抓住重点难点
虽然例题教学在课堂教学中的作用比较重要,但却不能占据太大的比重,也就是说例题的教学要少而精,尽可能多地涵盖刚学习的知识内容,这就对教师筛选例题的内容提出了很高的要求。因此,教师在设计例题时应切中要害,抓住重点,突破难点。
例如,为了向学生们强调数形结合思想的重要性,笔者在教学中引入了这样一道例题:一个面积是1的矩形,它的周长能够取得的最小值是多少?一个周长是3的矩形,它的面积能够取得的最大值又是多少?这两个问题看似简单,但当学生们列出了xy=1和2(x+y)=3这两个方程之后便会发现,想要靠目前所掌握的代数知识,很难轻松找到最值。于是,笔者引导学生将上述两个方程分别变形为y=和y=-x+,并一一画出反比例函数与一次函数的图象(如右图),周长的最小值与面积的最大值也就出现了。在这里,笔者特意选择了一道过程并不复杂的例题,从而让学生们的注意力不会向理解题目含义等方向分散,“数形结合”这一教学重点也就能被学生所关注了。可见,切中要害的例题内容选择对于推进课堂教学的效果是十分显著的。
二、适度灵活处理,不拘泥于课本
很多教师认为,既然例题是依据本次课堂教学的内容而设定的,对其进行解答时也应当严格按照本次教学内容中的思想方法展开。这种做法虽然可以强调例题的针对性,但也会造成学生的数学思维过于禁锢。适度地走出课本内容,对例题进行多角度的灵活处理,不仅能够将课堂内容讲解清楚,还可以开辟出更多的思考路径。
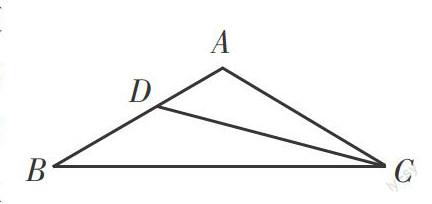
例如,在教学“等腰三角形”的内容时,笔者设计了这样一道例题:如下图所示,在△ABC中,∠A=100°,AB=AC,CD是∠C的平分线。求证:BC=CD+AD。这道题的证明方法很多,讲解时,笔者先向学生们讲解了通过在BC上截取CD=CE,以D为圆心并以DE长为半径作弧交BC于F,这样两次构造等腰三角形来转移等量线段的方式来证明的思维过程。这是紧贴等腰三角形的知识内容展开的,笔者将大部分精力放在了对于这种解题方法的分析上。随后,笔者又向学生们介绍了在BC上截取CD=CE,使得A、D、E、C四点共圆来证明的方式,以启发学生的其他思路。
当然,在运用多种方式解答例题时,教师也要把握好着力轻重的分布。依据本次教学内容而产生的解题方法,必然是教师所要强调的重点。其他解题方法则作为辅助方法即可。处理好这样的主次关系,才不会让课堂教学偏离主线。
三、及时调整视角,顺应学生心理
学生是数学知识的最终接受者,自然也就成为了初中数学教学的主体。因此,例题在为课堂教学服务的同时,实际上也是在为学生理解知识服务。由此,学生自身对于例题的感受如何,也就成为了评价例题教学开展效果的重要指标。教师在设计例题时,除了要让例题的内容与本次教学相契合,还要及时关注学生的心理,让例题得以最大程度地被学生接受。
例如,在教学“方程”这一比较抽象的内容时,笔者设计了联系实际的例题:①有一块四周镶有宽度相等的花边的地毯(如下图左),它的長是8米,宽是5米。如果地毯中央的长方形图案面积是18平方米,则花边的宽度是多少?②如下图右所示,靠在墙上的梯子长度为10米,梯子顶端距离地面的垂直高度是8米。如果梯子的顶端下滑了1米,则梯子的底端移动了多少呢?这两道例题,让学生在解决实际问题当中感受到了方程的应用价值,理解并接受这一思想方法也就自然了很多。
总之,想要通过例题的方式实现有效的初中数学教学也不是随意为之的。一要保证例题的存在是有意义的,是紧贴本次教学的重点难点的;二是对于例题的思考也不能被本次教学内容完全限制,不要让其失去启发学生思维的功能;三是站在学生的角度设计和处理例题,让学生们最大化地接受知识。
(责编 林 剑)

