行星轮系侧隙分析理论探讨❋

王 文，曹罚君，张跃春，陈 磊

（中航工业 株洲高精传动技术有限公司，湖南 株洲 412002）

0 引言

目前，齿轮副侧隙分析理论主要针对固定轴齿轮副而言，仅适用于齿轮轴有固定支撑且中心距偏差由箱体轴承座孔制造精度保证的情况。然而，在行星轮系传动中，太阳轮、齿圈为浮动件，中心距偏差取决于其浮动量的大小和行星销轴的位置度精度，因此，固定中心距的齿轮副侧隙分析理论不适用于行星轮系齿轮副侧隙分析。

当前，关于行星轮系齿轮副侧隙分析方面的理论很少，本文在充分研究固定中心距齿轮副侧隙分析原理的基础上，结合行星轮系的运动特性，通过均载分析理论估算出太阳轮、齿圈的浮动量，以浮动量为重要设计参数对行星轮系齿轮副侧隙分析理论进行深入的研究。

1 固定中心距齿轮副侧隙分析

文献［1］中介绍了固定中心距齿轮副侧隙分析理论，由该分析理论可知，齿轮副侧隙的主要作用是为了保证齿轮在啮合过程中能够得到充分的润滑、避免因齿轮受力变形和摩擦发热膨胀导致挤轧。齿轮副侧隙主要包括以下几部分：

（1）补偿由于温升而引起变形所必需的最小侧隙量jn1：

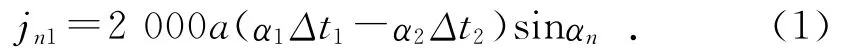
其中：αn为分度圆法向压力角，（゜）；a为齿轮副的工作中心距，mm；α1为齿轮材料的线膨胀系数；α2为箱体材料的线膨胀系数；Δt1为齿轮工作温度与环境温度之差，（゜）；Δt2为箱体工作温度与环境温度之差，（゜）。

（2）保证正常润滑所必需的最小侧隙量jn2，其值取决于齿轮传动时所允许的工作温度、润滑方式和齿轮的节圆圆周线速度等。

（3）补偿由齿轮副的制造误差和安装误差所引起的侧隙减小量Jn：

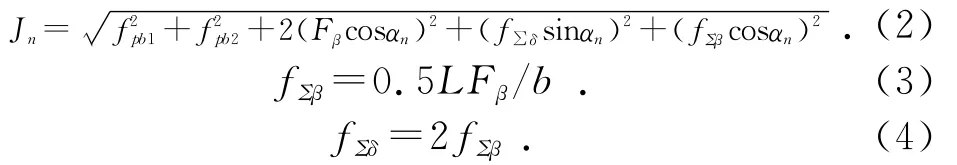
其中：L为轴承支承跨距，mm；b为齿轮齿宽，mm；fpb1，fpb2分别为大、小齿轮的基节极限偏差，μm；Fβ为螺旋线总公差，μm。

（4）齿轮副中心距极限偏差±fa。

综合考虑以上各因素，得到固定中心距齿轮副最小侧隙Jmin：

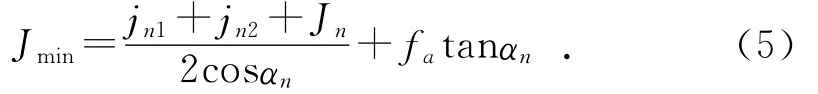
2 行星轮系齿轮副侧隙分析理论研究

通过对行星轮系的运动特性进行深入的分析，将行星轮系简化成合理的力学模型。然后依据均载分析理论，将太阳轮、齿圈的浮动量及各构件的制造误差转换投影到对应齿轮副的啮合线方向上得到当量啮合误差，再根据力学平衡条件，建立轮系的力学平衡方程组，联立求解即可得到太阳轮、齿圈的浮动量。最后，综合考虑太阳轮、齿圈浮动量的大小和行星销轴的位置度精度，并用该综合量替代固定中心距齿轮副侧隙分析理论中的中心距偏差，研究行星轮系齿轮副侧隙理论。

2.1 力学模型建立

整个行星轮系由太阳轮、行星轮、齿圈和行星架组成。将行星齿轮系传动机构的各构件看作质量－弹性体，啮合副、回转副及支承处的弹性变形用等效弹簧刚度表示，建立行星齿轮传动静力学模型［2－4］，如图1所示。本文只以星型传动为例进行研究，其他行星轮系传动结构可以此为基础进行研究。

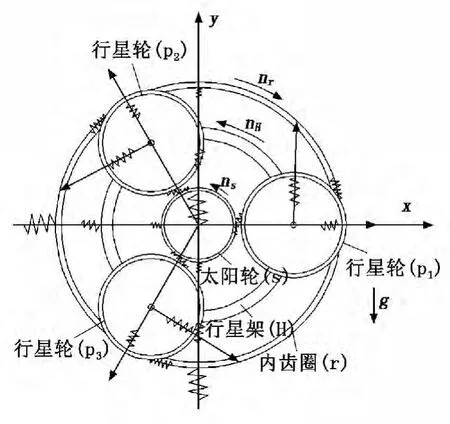
图1 行星齿轮传动静力学计算模型

2.2 当量啮合误差分析

行星轮系各轮之间的载荷分布不均及各轮的浮动主要是由于各轮存在当量啮合误差造成的。当量啮合误差主要由各轮的浮动量和制造误差两部分组成。

（1）太阳轮、齿圈浮动量引起的当量啮合误差。依据轮系几何关系［5－6］，将太阳轮和齿圈的浮动量转换至外、内啮合线上的当量啮合误差为xsdi和xrdi：

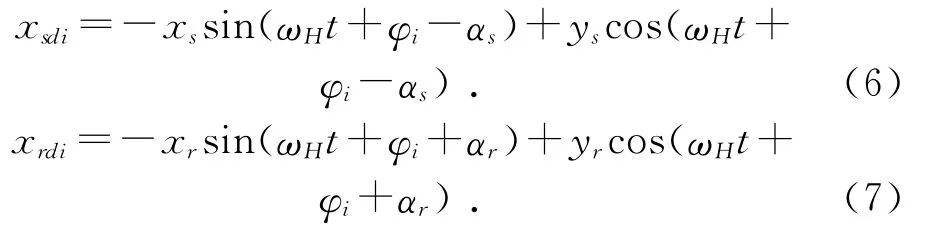
其中：xs和ys分别为太阳轮中心沿固定坐标系的x和y轴方向上的微小位移量，mm；ωH为行星架的转速，rad/s；t为行星轮运转的时间，s；φi为第i个行星轮中心和太阳轮中心的连线与x轴正方向的初始位置角，（゜）；αs和αr分别为齿轮副的外、内啮合角，（゜）；xr和yr分别为齿圈中心沿固定坐标系的x和y轴方向上的微小位移量，mm。

（2）制造误差引起的当量啮合误差。制造误差包括偏心误差、装配误差及各轮的齿厚公差等，通过理论分析与试验，证明行星架偏心误差和齿厚公差对均载和浮动量影响最大，依据几何关系，可将行星架偏心误差和齿厚公差转换至外、内啮合线上的当量误差。

行星架的制造偏心误差EH转换到太阳轮与第i个行星轮啮合线上的当量啮合误差为espi：

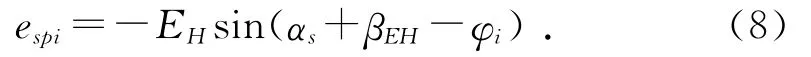
其中：βEH为行星架的制造偏心误差EH相对坐标系x轴正方向的初始位置角，（゜）。

行星架的制造偏心误差EH转换到齿圈与第i个行星轮啮合线上的当量啮合误差为erpi：

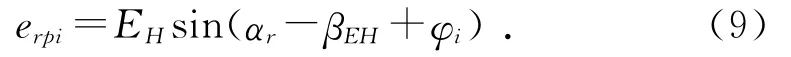
太阳轮齿厚公差εs转换到太阳轮与第i个行星轮啮合线上的当量啮合误差为esi：

齿圈齿厚公差εr转换到齿圈与第i个行星轮啮合线上的当量啮合误差为eri：

行星轮齿厚公差εp转换到太阳轮、齿圈与第i个行星轮啮合线上的当量啮合误差分别为epsi，epri：

将上述的当量啮合误差综合可得在太阳轮、齿圈与第i个行星轮啮合线上的综合啮合误差分别为Δspi，Δrpi：

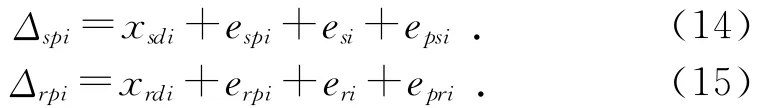
2.3 建立平衡方程求解太阳轮、齿圈的浮动量

分析力学模型中各轮的受力情况，建立各轮力学平衡方程，构建行星轮系的受力平衡方程模型，通过相关数值分析理论，求解太阳轮、齿圈的浮动量δsi和δri：

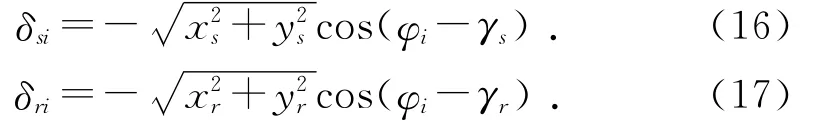
其中

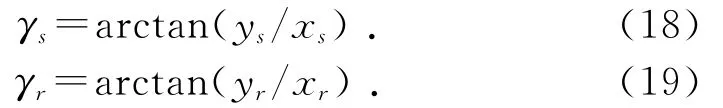
由于轮系各制造误差具有随机性，因此，需要分析较多行星轮样本，可得太阳轮、齿圈浮动量分布符合蒙特卡罗分布，取其3σ值表征轮系的太阳轮、齿圈浮动量。

2.4 行星轮系齿轮副侧隙分析

用太阳轮、齿圈的浮动量加行星销轴的位置度误差之和替代中心距偏差，可得行星轮系外、内啮合的侧隙J1min，J2min：

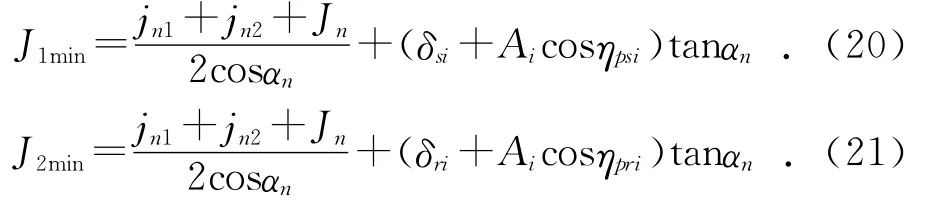
其中：Ai为第i个行星轮销轴的位置度误差；ηpsi为太阳轮与第i个行星轮的啮合线方向与该销轴的位置度误差方向的夹角；ηpri为齿圈与第i个行星轮的啮合线方向与该销轴的位置度误差方向的夹角。

3 结论

（1）深入研究了固定中心距齿轮副侧隙分析理论，指出该理论在行星轮系齿轮副侧隙分析中存在的局限性。

（2）结合行星轮系的运动特性，依据均载分析理论，在充分研究固定中心距齿轮副侧隙分析理论的基础上建立了行星轮系齿轮副侧隙的分析理论。该理论更加适合于行星轮系齿轮副侧隙的分析。

（3）均载理论比较适用于直齿且转速较慢的行星轮系，实时刚度、动态特性等因素影响斜齿和转速较快的行星轮系的力学模型，因此需要更加深入地研究其均载理论，才能得到较为可靠的浮动量。

［1］廖念钊，古莹菴，莫雨松，等.互换性与技术测量［M］.北京：中国计量出版社，2000.

［2］陆俊华，李斌，朱如鹏.行星齿轮传动静力学均载分析［J］.机械科学与技术，2005，24（6）：702－709.

［3］李阳，刘光磊，刘更，等.基于间隙浮动的行星齿轮传动系统静力学均载分析［J］.机械科学与技术，2009，28（8）：1115－1120.

［4］周惠琴，李素有，吴立言.行星齿轮传动系统均载分析［J］.机械科学与技术，2008，27（9）：1239－1242.

［5］鲍和云，朱如鹏.两级星型齿轮传动静力学系统基本浮动构件浮动量分析［J］.中南大学学报（自然科学版），2006，37（3）：553－557.

［6］朱龙英，朱如鹏，刘正埙.星形齿轮传动的均载研究［J］.机械工程师，2007（3）：43－45.