消耗速率为函数的应急调度模型及算法＊

李梅霞，潘爱霞

（潍坊学院，山东 潍坊 261061）

本文针对突发事件发生时，应急物资的调度问题进行深入研究。众所周知，应急问题最显著的特点表现在时间的紧迫性，决策者应以较短的时间完成调度方案。如何合理地调度救援物资成为国内外学者的一个重要研究课题［1-3］。在应急问题中，救援一旦开始，就有物资消耗，并且要尽量确保物资的充足供应。连续性条件就是要保证在任何时刻已到达物资量满足物资持续消耗，即不能出现因物资供应不足引起的应急活动的停止，这类问题普遍适合于诸如连续性应急生产系统，电力供应系统，供暖供气系统，消防系统以及其它复杂的社会系统。关于应急系统的研究成果已经广泛运用于森林火灾［4］、地震［5］、矿井塌陷［6］、辐射性废料泄漏事故［7］等具体灾害领域，但是这些研究都是在消耗速率为常数的情况下进行的。文献［8］中给出了消耗速率为函数的连续型应急资源调度模型，给出了最早应急时间的求解算法，但是没有考虑使得出救点的个数尽可能得少，而出救点个数的多少直接关系到出救成本，所以本文将在以上文献的基础上，首先给出应急时间最早时出救点个数最少的两阶段算法，并通过数值算例说明算法的应用。另外，在大型应急活动中，应急资源的需求是多样的，所以研究消耗速率为函数的连续型多资源应急调度模型具有更重要的实际意义，本文探讨了应急时间最早、出救点数目最少的多资源应急调度模型。该模型利用单资源最早应急时间的求解公式，得到了多资源最早应急时间的求解方法，进一步探讨了出救点数目最少的调度方案，并用数值算例验证了算法的有效性和实用性。

1 问题描述

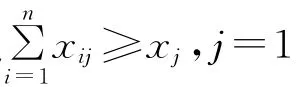
设νj（y）为第j种应急资源的消耗速率，j=1，2，…，l。

假设1 νj（y）为可积函数且νj（y）≥0，j=1，2，…，l。

设s为应急起始时间，fj为第j 种应急资源的应急结束时间，则

为了求解具有最早应急开始时间的方案，首先给出如下定义。

定义1 设消耗速率νj（y），j=1，2，…，l，满足假设1，如果对∀t∈［s，fj］，均有

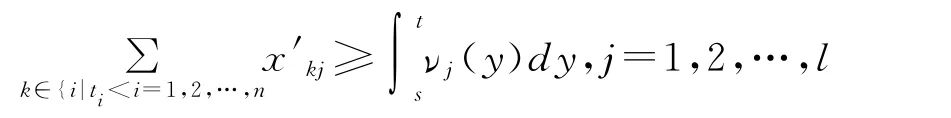
则称方案φ 关于起始时间s是j 资源连续可行的。

设所有关于起始时间s是连续可行的方案的集合为χs，此时问题就变为求解下述最优化问题

当j=1，即为单资源的应急问题。文献［8］中给出了单资源问题最早应急时间的求解算法，如下述几个定理所述。

定理1 假设t1≤t2≤…≤tn，应急时间最早的最优方案为

定理2 φ＊对应的最早应急时间为

其中，Tk由以下方式确定

2 单资源问题应急时间最早时出救点个数最少的两阶段算法

文献［8］给出了对应最早应急时间的最优方案和最早应急时间的求解算法，但是给出的最优方案φ＊中可能包含了太多的出救点，从系统的稳定性和费用角度出发，我们更希望求出的方案在不延迟应急开始时间的前提下包含出救点的个数尽可能少，因为出救点的多少直接关系到系统的稳定性和可靠性，并且从费用角度看，出救点的多少又直接关系到系统的总设置费用。许多文献在设计应急点的分布时也十分强调这一因素。

设N（φ）表示方案φ 中出救点的数目，在文献［8］中，N（φ＊）=p，希望求解如下问题

［1］中的方法，给出如下的算法，依据是在相同的出救时间的前提下，为了减少出救点的数目，尽量的挑选物资量多的出救点进行出救。

算法1

（1）u=s＊，k=1，total=0，I=Φ。

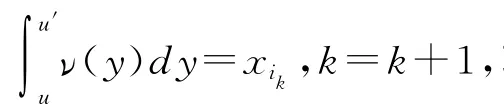
（4）φΛ=｛（Ai1，xi1），（Ai2，xi2），…，（Aik-1，xik-1），（Aik，xik′）｝。

类似于文献［1］中的处理方法，为了方便讨论，对算法1的步骤（2）稍作修改，得到如下的算法。

算法2 （χs≠φ）

（1）u=s＊，d=1，total=0，I=Φ。

（2）∀jd∈｛j｜tj≤u，j∉I｝，I=I+｛jd｝，转（3）。

（4）φ=｛（Aj1，xj1），（Aj2，xj2），…，（Ajd-1，xjd-1），（Ajd，xjd）｝。

设算法2产生的所有可能的方案的集合为χs′。

类似于文献［1］中相关定理的证明可以得到如下的几个引理和定理，在此将证明过程省略。

引理1 当χs≠φ时，通过算法2求得的任一方案是连续可行的，即χs′⊂χs。

引理2 当χs≠φ时，存在一方案φ∈χs′使得问题（2）达到最优。

定理3 当χs≠φ时，设通过算法1求得的方案为

并且假定

是通过算法2求得的任意一个方案，则k≤d。

定理4 算法1给出的解是问题（2）的最优解。

例1 对于文献［1］中的例1，各出救点的物资量及出救时间见表1。

表1 各出救点的物资量及出救时间

假设物资需求量为300，物资消耗速率

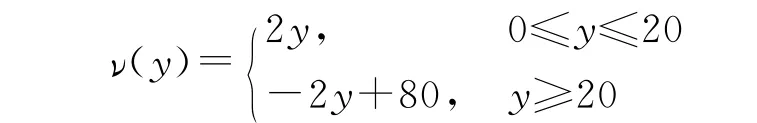
根据文献［1］中的计算可知

按照本文给出的算法1，在最早应急开始时间不变的情况下，得到最优方案为

因此只需要5个出救点就可以了，这样减少了出救点的数目，既可以达到经济的目的，又可以增加出救的可靠性。

3 多资源问题应急时间最早出救点个数最少的算法探讨

本节将探讨多资源问题的调度模型。文献［9］中给出了多资源应急问题最早应急时间的求取方法。首先针对每一种资源求解下面的优化问题：

令

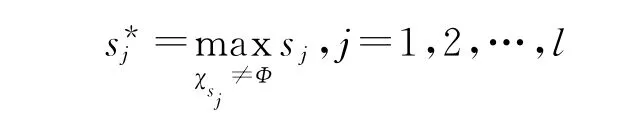
其对应的最优方案为

其中，pj满足

易知，对任意的j，有φ＊j∈

令

由文献［9］中的相关定理可知下述定理成立。

定理5 （3）式表示的方案φ＊是问题（1）的最优方案，并且最优目标值为s。

定理5给出了多种资源最早应急时间的求解方法。在保证应急时间最早的情况下，出救点个数的多少直接影响出救的成本。因此在求出最早应急时间后，可以根据第3节中的方法，针对每种资源确定出救点数目最少的调度方案，然后适当地调整每一种物资的出救点，使得在最早应急时间不变的情况下，出救点的个数尽可能的少。

下面通过几个例子探讨多资源物资调度问题在应急时间最早的情况下，出救点个数最少的调度方法。

例2 设事故发生点A 需要三种物资，需求量为x=（20，30，92），各出救点Ai的资源可用量xij及到达A 的行走时间ti见表2。

物资的消耗速率

表2 各出救点的物资量及行走时间

按照第2节的计算方法，首先计算每一种物资的出救方案和最早应急时间

所以最早应急时间为s＊=20.2，共需要7个出救点。

按照第3节给出的方法，在保证最早应急时间s＊=20.2不变的情况下，将出救方案进行调整，目标是使各种资源的出救点数目尽可能得少。调整方案如下

由上述结果知，三种资源中均需要A2，A4，A5三个出救点，所以该三点不必进行调整。为了减少出救点的数目，尽量去除运送时间大的出救点，因此首先考虑去掉第三种资源中的A7点，而A3点的供应量为4，小于φ3′中A7点的供应量8，所以不能将A7点换为A3点。既然第三种资源中的A7点不能去掉，下面考虑在第一种资源中将A6点换为A7点。通过计算可知，从s＊=20.2至A7点的运送时间23时的消耗量为23.5，大于A1至A5的供应量之和16，所以也不能将A6点换为A7点。由以上分析知，以上的调运方案无法进行优化，仍然需要7个出救点。

例3 设事故发生点A 对三种物资的需求量分别为60，100，120，各出救点Ai的资源可用量xij及到达A 的行走时间ti见表3。

表3 各出救点的物资量及行走时间

物资的消耗速率

按照第2节的计算方法，首先计算每一种物资的最优出救方案为

每一种资源的最早应急时间为s1＊=1.8，s2＊=1，s3＊=1，所以最早应急时间为s＊=1.8，共需要8个出救点。

按照第3节给出的方法，类似于例2的分析，可以在保证最早应急时间s＊=1.8不变的情况下，将出救方案调整如下

根据上述方案可以看出，只需要7个出救点就可以完成救援。

4 结论与展望

本文针对应急系统多点出救的特点，首先研究了单资源应急调度模型中应急时间最早、出救点个数最少的两阶段模型，然后探究了消耗速率为函数的连续型多资源应急调度模型。该模型是通过计算每种资源的最早应急时间得出多资源模型的最早应急时间，进而探讨了应急时间最早、出救点数目最少的多资源调度方法。数值算例表明了算法的有效性和实用性。对于多资源的连续消耗的应急问题，应急时间最早、出救点数目最少的系统算法的设计是我们亟需研究的重要问题。

参考文献：

［1］刘春林，何建敏，施建军.一类应急物资调度的优化模型研究［J］.中国管理科学，2001，9（3）：29-36.

［2］Barbarosoglu G，Arda Y A.Two-stage stochastic programming framework for transportation planning in disaster response［J］.Journal of the Operational Research Society，2004，55：43-53.

［3］赵林度，刘明，戴东甫.面向脉冲需求的应急资源调度问题研究［J］.东南大学学报：自然科学版，2008，38（6）：1116-1120.

［4］Jean-Luc，Wybo.FM IS：a decision support system for forest fire prevent ion and fighting［J］.IEEE Transactions on Engineering，1998，45（2）：127-131.

［5］Walter W.Hays.Reduction of earthquake risk in the United States：bridging the gap between research and practice［J］.IEEE Transact ions on Engineering Management，1998，45（2）：176-180.

［6］Henry P，Cole.Decision making during a simulated mine fire escape［J］.IEEE Transactions on Engineering Management，1998，45（2）：153-162.

［7］George F，List.Routing and emergency-response-team siting for high-level radioactive waste shipments［J］.IEEE Transactions on Engineering Management，1998，45（2）：141-152.

［8］李梅霞，车海涛.应急资源调度模型及算法［J］.运筹与管理，2011，20（3）：72-76.

［9］郑昊，高岩.多资源消耗应急系统调度模型及算法［J］.上海理工大学学报，2013，35（5）：415-419.