扩展KP方程的周期波解以及可积性质＊

高 静

（中国矿业大学，江苏 徐州 221116）

1 引言

利用双线性算子寻求非线性方程的双线性表示，Lax对和Bäcklund变换是孤立子理论的研究方向之一，日本数学家Hirota［1］开辟了这一先河，随后中国科学院的胡星表［2-3］等国内学者利用双线性化方程导出了许多非线性方程的双线性表示、Lax对、Bäcklund变换、无穷守恒律等系列问题。在1980年，Nakamura基于Hirota双线性方法提出了求解非线性方程的多周期波解的综合方法［4-5］，这种方法的优点在于它只依赖Hirota双线性形式。可是，寻求一个非线性演化方程的双线性变换并非易事，需要作出恰当变换，寻求该变换具有很强的技巧性，为解决这一问题，Lambert等人［6-7］引进了Bell多项式方法，使得寻求非线性演化方程的双线性表示有了一定的规律。在此基础上，范恩贵［8-9］等学者将Bell多项式应用于变系数的非线性演化方程中，得到了变系数KdV 方程、KP方程等的可积性质。本文利用Riemann theta函数理论和Bell多项式有关理讨论扩展KP方程的可积性质。

为此，我们首先回顾一下Riemann theta函数和Bell多项式的基本理论。

2 Riemann theta函数与Bell多项式

定义1 Hirota双线性算子

其中X′=（x′1，x′2，…，x′N）。

性质1 Hirota双线性算子Dx1，Dx2，…DxN，Dt有如下性质

其中ξi=kix1+lix2+…+σixN+ωit+εi，i=1，2，ki，li，…，σi，ωi，εi是常数。此外，我们有

其中F（Dx1Dx2，…，DxN，Dt）是关于双线性算子Dx1，Dx2，…，DxN，Dt的多项式。这些性质在导出Hirota双线性形式以及构造非线性方程的周期波解方面具有重要作用。下面我们介绍Riemann theta函数以及它的周期性。

定义2 Riemann theta函数

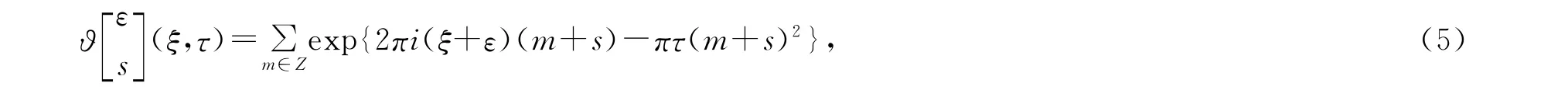
其中，m∈Z，参数s，ε∈C，变量ξ∈C，τ＞0是Riemann theta函数的周期矩阵。

定义3 设g（t）是复数域C 上周期函数，基本周期T1，T2，…，Tk∈C，如果T1，T2，…，Tk是线性依赖于整数Z 且存在Ck上的函数G（y1，y2，…，yk）满足

那么g（t）是复数域C 上的拟周期函数。

特别地，当k=2时，g（t）称为是双周期函数，当且仅当Tj=mjT 时，g（t）是关于周期T 的周期函数。

性质2 Riemann theta函数ϑ（ξ，τ）具有周期性

特别地，我们把向量l和iτ 称为是ϑ（ξ，τ）关于乘数l和exp（-2πiξ+πτ）的周期。

性质3 设f（ξ）是复数域C 上的亚纯函数

则有

也就是说f（ξ）是关于l和iτ 的周期函数。

其中，∑μ=0，1是关于μ=0，1的两种不同的变换。x，y，t的双线性公式由∂x，∂y，∂t代替。

一般地，关于算子Dx，Dt，Dy的多项式算子F（Dx，Dt，Dy）则有下面重要的公式

其中

由（11）和（12）式我们可以知道如果

的周期波解。

公式（13）为我们提供了求解非线性方程周期波解的独一无二的方法。只要求出方程的双线性形式，那么我们可以从公式（13）中直接获得它的周期波解。

定义4 设f=f（x1，x2，…，xn）是具有n个变量的C∞函数，则称

为多维Bell多项式。特别地，当f=f（x，t）时，由（15）可得

设

则这种只含有函数v和w 的Bell多项式称为双Bell多项式。由（17）式可得

二元Bell多项式与Hirota双线性D 算子之间有如下的关系

其中，n1+n+…+nl≥1。特别的，当f=g 时，由（19）式可得

由（20）式可得

根据双线性算子和Hopf-Cole变换v=lnΨ 之间的关系。特别地

下面，我们利用以上理论，讨论扩展KP 方程的周期波解以及可积性质，包括双线性表示、Lax 对、Bäcklund变换和无穷守恒律。

3 方程（1）的周期波解与可积性质

在方程（1）中，令u=q2x，积分两次可得

其中，c为积分常数，令

所以

令q=2lnf⇔u=q2x=2（lnf）2x，则方程（1）的双线性导数形式为

在求解孤子解时常数c可以为零，但在求周期波解时非零常数c具有重要作用，在应用时不可以省略。

当c=0时，方程（1）的单孤子解

其中，η=kx+ry+ ［（k4+3y2+3k2）／k ］t+h，k，r，h 是常数。下面我们讨论（23）的周期性。函数f 选作Riemann theta函数，也就是说，

其中，变量ξ=αx+βy+ωt+σ。由性质3可得

即孤子解u是关于基本周期l和iτ 的周期函数。

引进如下的记号

把（28）带入（26），利用公式（13）和（30），可以得到如下的线性关系：

其中

由（31）式我们可以得到ω，c的精确解

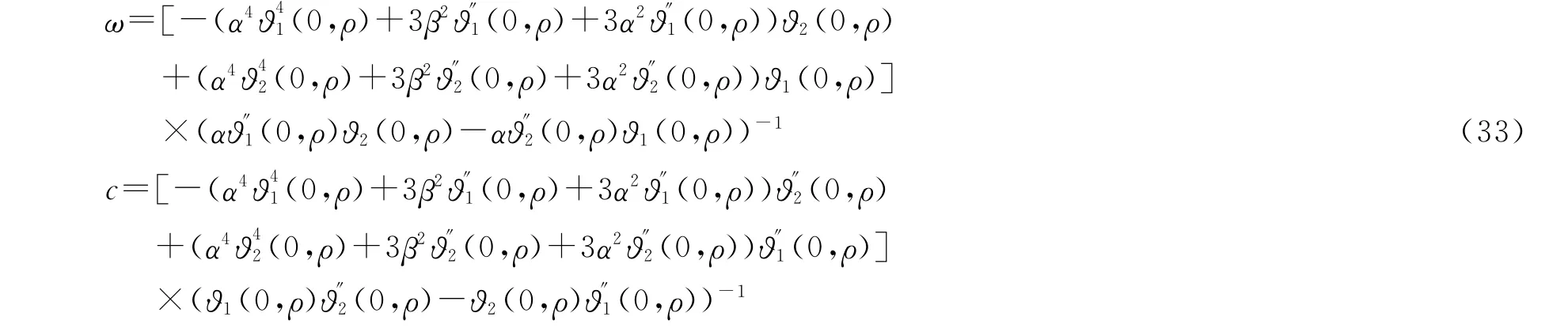
因此，我们得到方程（1）的周期波解

其中，ϑ（ξ，τ）是由（4）式给出，且s=ε=0，参数ω，c由（33）式给出，其它的变量α，β，σ都是自由的。

下面我们讨论周期波一些特征以及渐进性质。周期波解（34）具有如下一些简单性质。

（1）关于变量ξ是一维的。

（2）关于变量ξ有两个基本周期l和iτ。

（3）速度参数ξ是由

给出。

（4）在一个周期中，只有一个波模式，可以视为是一个平行叠加重叠的孤子波。

现在，我们更深一层的讨论周期波解的渐进性质。即周期波解（34）和单孤子解（27）它们之间有如下的关系。

定理2 如果向量（ω，c）T是（31）式的一个解并且是（33）式的周期波解，令

其中k，γ，h是由（27）式给出，那么有如下的渐进关系，当ρ→0时，

这说明在一个很小振幅限制下，周期波解（34）趋近于单孤子解（27），即当ρ→0时

证明 我们把（31）式的系数展开则有

把（31）式的解写成如下形式

把（39）式和（40）式代入（31）式，根据第二个方程ρ的系数，令ρ→0，则我们可以立即得到如下的关系

有下面的解

结合（36）和（41）当ρ→0时

因此，我们可以得到如下结论，当ρ→0时

接下来，我们讨论当ρ→0时，周期波解（34）式的渐进性质。把Riemann theta函数ϑ（ξ，τ）展开，并利用（44）式的表达式，有如下结论，当ρ→0时

所以，我们有当ρ→0时，周期波解（34）趋近于孤子解（27）。

下面我们讨论方程（1）的可积性质：

其中

令

则有

故（47）式可以化为

（51）式两边对x 积分，并取积分常数为零可得

由（49）和（52）式可得方程（1）的Bäcklund变换，

设υ=lnψ，ω=υ+q 由（22）式可知

因此，由方程（49）和（52），我们可以得到方程（1）的Lax对

把（56）式代入（49）式，得到Riccati-type方程

把（56）式代入（52）式，得到divergence-type方程

令

并代入（57）式，我们得到In的递推关系式

把（59）代入（58）可得，

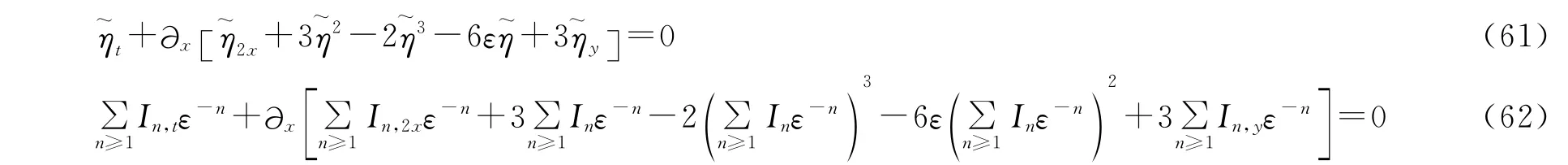
因此，我们得到方程（1）的无穷守恒律

其中

［1］Hirota R.The Direct Method in Soliton Theory［M］.Cambridge：Cambridge University Press，2004.

［2］Hu X B，Clarkson P A.Rational solutions of a differential-difference KdV equation，the Toda equation and the discrete KdV equation［J］.J Phys A：Math Gen，1995，28（17）：5009-5016.

［3］Hu X B，Li C X，Nimmo J J C，Yu G F.An intergrable symmetric（2+1）-dimensiona-l Lotka-Volterra equation and a family of its solutions［J］.J Phys A：Math Gen，2005，38（1）：195-204.

［4］Nakamura A.A direct method of calculating periodic wave solutions to nonlinear evolution equations（I）：Exact two-periodic wave solution［J］.Journal of the Physical Society of Japan，1979，47（5）：1701-1705.

［5］Nakamura A.A direct method of calculating periodic wave solutions to nonlinear evolution equations（Ⅱ）：Exact one-periodic and two-periodic wave solution of the coupled bilinear equations［J］.Journal of the Physical Society of Japan1980，48（4）：1365-1370.

［6］Lambert F，Springael J.Soliton equations and simple combinatorics［J］.Acta Appl Math，2008，102（2／3）：147-178.

［7］Lambert F，Loris I，Springael J.Classical Darboux Transformations and the KP Hierarchy［J］.Inverse Problems，2001，17，1067-1074.

［8］Fan E G.The integrability of nonisospectral and variable-coefficient KdV equation with binary Bell polynomials［J］.Phys Lett A，2011，375：493-497.

［9］Fan E G，Chow K W.Darboux covariant Lax pairs and infinite conservation laws of the（2+1）-dimensional breaking soliton equation［J］.J Math Phys，2011，52（2）：023504.

［10］Wang Y H，Chen Y.B cklund Transformations and Solutions of a Generalized Kadomtsev-Petviashvili Equation［J］.Commun Theor Phys，2012，57（2）：217-222.