基于Lagrange函数的线性规划对偶问题研究

向彦宁，李永玲

(重庆师范大学 数学学院，重庆　401331)

基于Lagrange函数的线性规划对偶问题研究

向彦宁，李永玲

(重庆师范大学 数学学院，重庆401331)

摘要：运用非线性规划的Lagrange对偶原理，对线性规划的弱对偶、强对偶进行了证明，并通过极小-极大对偶性Lagrange函数详细证明了线性规划在不同的约束条件下的对偶形式。

关键词：非线性规划；线性规划；Lagrange对偶；对偶问题

线性规划问题通常被定义为：在满足一定的约束条件下，求得目标函数的最优值。通常考虑如下形式的线性规划问题(LP)[1]：

(1)

其中x=(x1，x2，…，xn)t，A=(aij)m×n，b=(b1，b2，…，bm)t，c=(c1，c2，…，cn)t。

定义其对偶问题(DP)为[1]：

(2)

其中y=(y1，y2，…，ym)t为列向量。问题(2)为原问题(1)的对偶问题，问题(1)与问题(2)是一对对称的对偶规划问题。

在线性规划理论中，线性规划的对偶问题是非常重要的部分，但在一般的文献和高校教材中[1-5]，线性规划的对偶问题是求最大值、最小值，约束条件为等式和不等式，变量是大于等于零或者是任意的，因此对于不同约束条件形式的对偶证明比较繁琐。

本文在第2节中给出了非线性规划的Lagrange对偶；在第3节中证明了线性规划原问题(1)的对偶性质(强弱定理)；第4节详细证明了线性规划在不同约束条件下的对偶。

1预备知识

考虑下面的非线性规划问题(NLP)[9]：

(3)

其中函数f:Rn→R，g:Rn→Rm，h:Rn→Rl是向量函数，则Lagrange对偶问题(NDP)为[9]：

其中θ(u，v)=inf{f(x)+utg(x)+vth(x):x∈X}。

注：Lagrange对偶函数θ对某些向量(u，v)可取值为-∞，与不等式约束g(x)≤0相应的Lagrange乘子u是非负的，与等式约束h(x)=0相应的Lagrange乘子v不受符号影响。

引理1设X是Rn的非空，α:Rn→R和g:Rn→Rm，h:Rn→Rl是凸的向量函数。如果下面的组1无解，则组2有解(u0，u，v)；如果u0>0，相反的结论成立[9]。

组1α(x)<0，g(x)≤0，h(x)=0，对于某个x∈X。

组2u0α(x)+utg(x)+vth(x)≥0，对任意的x∈X，(u0，u)≥0，(u0，u，v)≠0。

2线性规划的对偶性质

在本节中通过非线性规划的Lagrange对偶来研究原问题(1)与对偶问题(2)之间的关系。原问题(1)可变形为：

(4)

其中x=(x1，x2，…，xn)t，A=(aij)m×n，b=(b1，b2，…，bm)t，c=(c1，c2，…，cn)t。按照非线性规划的对偶原理引入Lagrange乘子u≥0，其Lagrange对偶问题为：

(5)

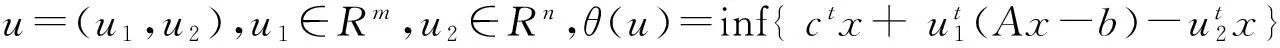
以下将非线性的 Lagrange对偶方法用在文献[10]上，更加简单地证明了线性规划的强、弱定理。

定理1弱对偶性定理

注：原问题的可行解的目标函数值是对偶问题目标函数值的上界。

推论2如果inf{ctx|Ax-b≤0，x≥0}=-∞，则对任何u≥0，θ(u)=-∞。

定理2强对偶性定理

min{ctx:Ax≤b，x≥0}=max{θ(u):u≥0}

(6)

证明设K=inf{ctx:Ax-b≤0，-x≤0}，如果k=-∞，由定理1的推论2得maxθ(u)=-∞，故式(6)成立。现假设K为有限值，则考虑系统：

(7)

按照K的定义，ctx≥K，所以式(7)无解。由引理1，必存在(a0，a)≥0，a0，a不能同时为0，a=(a1，a2)，使得

(8)

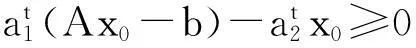
3线性规划在不同的约束条件下的对偶形式

本节先引入极小极大对偶性Lagrange函数[6]：

设x∈X⊆Rn，y∈Y⊆Rn，X，Y是非空集合，则极小极大对偶性Lagrange函数为

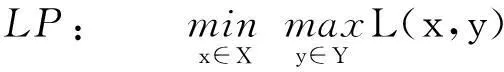
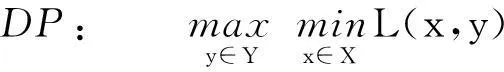
接下来考虑不同约束条件下的线性规划问题LP和DP。

注：“!≥”表示不大于等于。因为向量b-Ax=(c1，c2，…，cm)t≥0，表示每个ci≥0(i=1，2，…，m)，b-Ax=(c1，c2，…，cm)t!≥0表示∃ci<0，故“!≥”不等于“<”。

1) 约束条件为Ax≤b，x≥0的原、对偶问题：

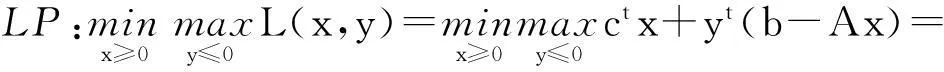
(9)

(10)

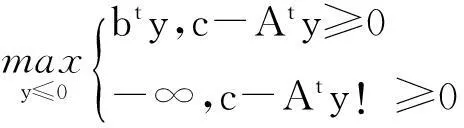
(11)

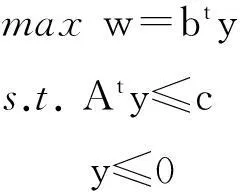
(12)

其中y=(y1，y2，…，ym)t为列向量。通过极小极大对偶性Lagrange函数得出式(9)与(10)等价，式(11)与(12)等价，又因为式(9)与(11)为一对Lagrange对偶，所以式(10)与(12)是一对对称的对偶规划问题。式(10)刚好就是为原问题(1)，式(12)为原问题的对偶问题(2)。

2) 约束条件为Ax=b，x≥0的原问题LP:

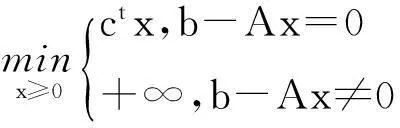
(13)

(14)

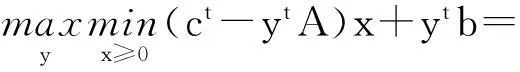
(15)

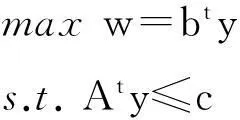
(16)

由上面极小极大对偶性得到问题(13)与问题(14)等价，问题(15)与问题(16)等价。又因为问题(13)与问题(15)为一对Lagrange对偶，所以问题(14)与问题(16)是一对对称的对偶规划问题。

同样按照极小极大对偶性Lagrange函数原理可以得到如表1所示的另外4种情形。

表1　另外4种情形

参考文献：

[1]运筹学教材编写组.运筹学[M].3版.北京：清华大学出版社，2005.

[2]刘云志,郭嗣琮.含直觉模糊弹性约束的模糊线性规划求解[J]. 系统工程理论与实践,2013(8):2027-2032.

[3]吴东华,夏洪山.基于多目标模糊线性规划求解方法的飞机排班问题研究[J].计算机科学，2012(1)：234-238.

[4]盛仲飙 .基于Matlab的线性规划问题求解[J]. 计算机与数字工程,2012(10):26-27,80.

[5]刘年磊,毛国柱,赵林.基于强化区间线性规划方法的流域环境系统管理优化[J]. 天津大学学报,2012(1):21-28.

[6]李师正，李刚.非线性规划的对偶原理[J].山东科学，1999，12(2):1-7.

[7]李师正，李刚.带有等式约束的非线性规划的对偶问题[J].山东科学，1999，12(3):1-5.

[8]张立卫.锥约束优化[M].北京:科学出版社，2010.

[9]Bazaraa M S，Sherali H D，Shetty C M.Nonlinear programming:theory and algorithms[M].[S.l.]:John Wiley & Sons，2013.

[10]卢开澄.线性规划[M].北京:清华大学出版社，2009.

(责任编辑陈艳)

收稿日期：2014-12-24

基金项目：国家自然科学基金资助项目(11431004)

作者简介：向彦宁(1990—),男,重庆万州人,硕士研究生,主要从事运筹学和控制优化研究。

doi:10.3969/j.issn.1674-8425(z).2015.07.021

中图分类号：O174

文献标识码：A

文章编号：1674-8425(2015)07-0116-04

DualProblemResearchofLagrangeFunction
BasedonLinearProgramming

XIANGYan-ning,LIYong-ling

(SchoolofMathematicalSciences，ChongqingNormalUniversity，Chongqing401331,China)

Abstract:Using the Lagrange principle of duality for nonlinear programming, linear programming duality of weak and strong duality was proved, and using the min-max Lagrange duality function, we proved that there is dual under different constraints in linear programming.

Key words:nonlinear programming; linear programming; Lagrange duality; dual problem

引用格式：向彦宁，李永玲.基于Lagrange函数的线性规划对偶问题研究[J].重庆理工大学学报：自然科学版，2015(7):116-119.

Citationformat：XIANGYan-ning,LIYong-ling.DualProblemResearchofLagrangeFunctionBasedonLinearProgramming[J].JournalofChongqingUniversityofTechnology:NaturalScience，2015(7):116-119.