电偶极子对电容参数影响分析
李 春
(上海航天技术基础研究所,上海 201109)
0 引言
电容测试筛选发现老化后容量值与初测值相较有偏差,尤其是瓷介电容器老化筛选后放置一段时间容量仍有偏差,且部分有机介质电容的容量值偏差超过了标称允许范围,影响测试结果,其中多数出现容量变小,老化结束放置一段时间后,容量又有所恢复,恢复的程度和时间不同。破坏性物理试验发现,这些电容的内电极无明显异常。目前,国内各生产厂老化后测试均参照各类电容的国军标执行,统一规定放电时间约24h,并未因材料区别而有其他特殊要求。
为此,本文对老练后电容解容量、损耗变化的原因进行了研究,讨论了去老练应力时间。
1 电偶极子与电偶极矩
1.1 电偶极子
电容中充满着电介质,每个电介质的分子中有正、负电荷。受外电场作用时,正、负电荷分别集中于一点,相隔一定距离,且电量相等,则该分子为电偶极子。根据电介质分子的结构可分为极性分子与非极性分子[1-4]。外电场场强越强,电偶极子产生的电矩就越大,微观角度解释如下[5-6]。
a)非极性分子主要有电子极化、原子极化两种。电子极化是指在外电场中每个原子的价电子云相对原子核发生位移,原子极化是指在外电场中不同的原子核间发生相对位移。随着外电场的场强增大,正、负电荷做的功增加,间距增加,电偶极矩增大。该极化亦称为变形极化。
b)极性分子极性分子的正负电荷重心本不重合,自身带固有偶极子,除变形极化外,还有取向极化。取向过程要克服本身惯性与旋转阻力,随着外电场的场强增大,取向极化更整齐,电偶极矩增大。分子热运动使偶极子的取向趋于杂乱,故取向极化还与温度有关。
1.2 外电场作用下受力

离偶极子很远处,即r≫|l|时,|r+|=|r-|≈r。此处:r为电子至点P的距离。则点P的总场强

因r+—r-=-l,则
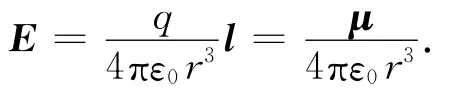
由上述分析可知:在电偶极子中垂线方向距离偶极子较远处的场强与电偶极矩成正比,与电偶极矩方向相反。由总场强公式,根据矢量三角形可推导出非中垂线上的场强也有相同的表达式。
外场强E0增大,正负电荷距离增大,则E变大,μ也随距离增大而增大,即随E0变大。
因存在电偶极子及自身在外电场中受力作用,产生了与外场强方向相反的电场强度,整体上削弱了原外电场强度,这种削弱场强随外电场场强增强而增强。
用电极化强度p表征总的单位体积内电偶极强度,有
桥梁模板是高速公路桥梁建设施工时用来固定桥梁的,同时也是施工中最重要的。在构架桥梁模板之前,首先需要计算机模拟技术构建出空间立体图纸,根据图纸进行模板拼接。模板构架材料一般采用可塑性较好的钢材,每节模板高度约为1.5m。模板材料定形以后,为了保证模板拼接后的稳定性还需对模板材料进行二次加工,保证模板表面光滑、平整,同时也方便模板的拆装。

式中:ε0为真空介电常数;εR为相对介电常数;μi为每个电子产生的电矩;ΔV为单位体积;E为电场强度。
1.3 介电常数
两块平行放置的金属板间为真空状态,两金属板带有+Q,-Q等量电荷,用电压计测得电压为V0。使平行板间充满绝缘介质,保持两平行板上电量不变,测得电压为V,因V=V0/εR,则V变小,又因V=Ed,V0=E0d,故E=E0/εR。此处:d为两极板间距离。
电偶极子的极化在金属板上产生与金属板极性相反的电荷,金属板表面电荷减小,电荷密度也减小,表现为场强减小,电场强度为原来的1/εr,且可推导由极化产生的反向电荷密度与极化强度一致,即

极化中,变形极化主要取决于分子电子云的分布,故变形极化随外电场强度而变,而取向极化则需克服本身惯性、旋转阻力及分子热运动,取向极化相对变形极化为时间的函数。变形极化产生的介电常数εC,取向极化产生的介电常数为εr。
2 容量变化
老化后,多层片式叠层电容的容量变化较常见,本文主要研究平行板结构的电容器。由高斯定律,电容容量

式中:S为极板面积。可见C与本身所带电量Q和两端电压V无关,仅与电介质本身性质和S,d有关。
对极性分子的取向极化时,需克服分子本身的黏滞系数、分子间热运动,可知极化和去极化过程与温度和时间有关,故极化强度是关于场强、温度和时间的函数,但式(3)并未体现,因此以电容本身定义式分析容量变化。
为便于分析容量变化趋势,老化后立即测试,不考虑降温及时间影响,变形极化完全缘由场强变化,而相同测试电压产生的变形极化相同,产生的反向电荷密度测试前后无变化,仅考虑由取向极化产生电荷密度的变化。
设额定电压100V,测试时电压1V,老化时在温度125℃加老化电压200V。由式(1)、(2)可得
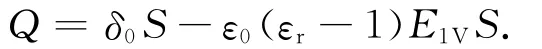
式中:δ0为无介质时极板上的电荷密度,且δ0=ε0ES。
将式(4)代入C=Q/V,则原始容量

老化 后 测 试 电 压 不 变,但Q=δ0S—ε0(εr—1)E200VS,故
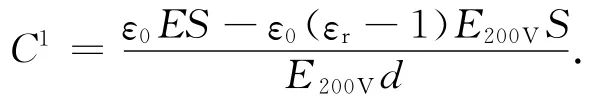
式中:E1V,E200V分别为1,200V 时的场强;C1为老化后容量。
因E200V>E1V,C1<C0,即容量变小,且C0=ε0εrS/d,与式(3)相同,满足电容定义。
容量变小时,根据电容定义式,ε0,d,S为定量,比较两式,老化后使εr变小。
3 损耗变化
3.1 极化过程
分析电介质在电场中的极化过程,平衡态的束缚电荷非瞬间产生,而是随时间延长不断增加,最后达到平衡态。交变电场中,极化过程应为电场变化频率的函数。从极化机理上看,变形极化速率较快,跟得上电场变化,而取向极化需一定时间达到平衡,未必能跟上电场变化,因此将其分为两部分:

式中:δC为瞬时产生的电荷密度,且
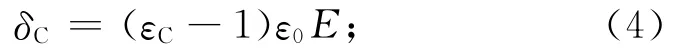
δD为随时间而产生的电荷密度,足够长时间后电荷密度达到δDR。此处:εC为瞬时介电常数。有

式中:εr为瞬时介电常数。由式(4)、(5)得
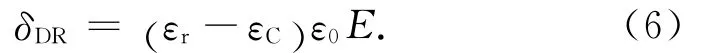
从动力学考虑,δD(t)变化到δDR速率与其偏离平衡态的程度成正比,则
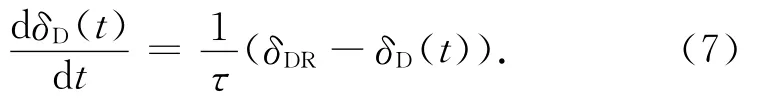
式中:1/τ为比例系数。
将式(6)代入式(7),整理后
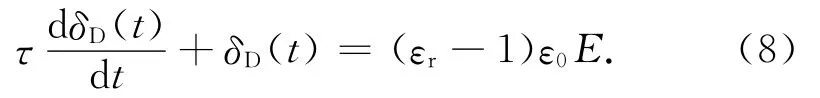
3.2 损耗变化
测试中使用频率1kHz或1MHz、电压1V的测试电压,其场强亦是交变的,则E(ῶ,t)=E0×exp(jῶt)。此处:ῶ为交流电压的角频率;j为虚数单位。此时,式(8)的微分方程中通解e-t/τ→0,则
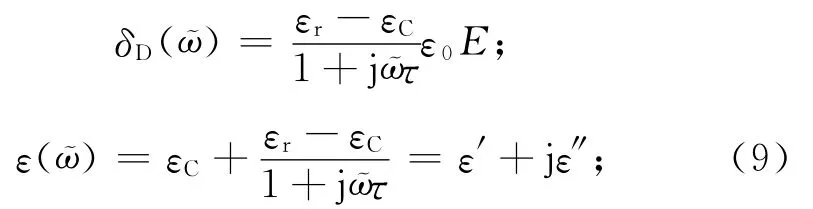
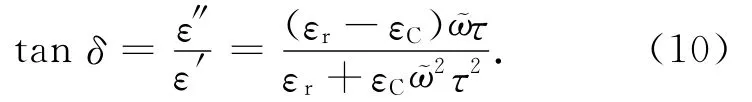
式中:ε′,ε″分别为ε(ω)的实部和虚部。
4 其他因素影响
由上述分析可知:除外场强外,温度和时间均会影响电容。以电偶极子为例,外场强为零时,其三维方向的能量分布完全相同,偶极子一端在原点,另一端出现在以偶极子长度为单位长度,球面各点θ至θ+dθ圆环上概率与环面积2πsinθdθ成正比,平均偶极矩为零。当外电场为E,偶极子的位能与其方向有关,偶极子与电场方向夹角为θ,设其形变偶极矩为μ0,则位能变化ΔU=-Eμ0cosθ。由玻尔兹曼关系,电偶极子出现在方向夹角为θ区域的概率与exp[-ΔU/(kT)]成正比。此处:kT为热学温度。由此产生的偶极矩μ2为μ0cosθ,平均值

将exp[-Eμ0cosθ/(kT)]以级数形式展开,略去高次项,得
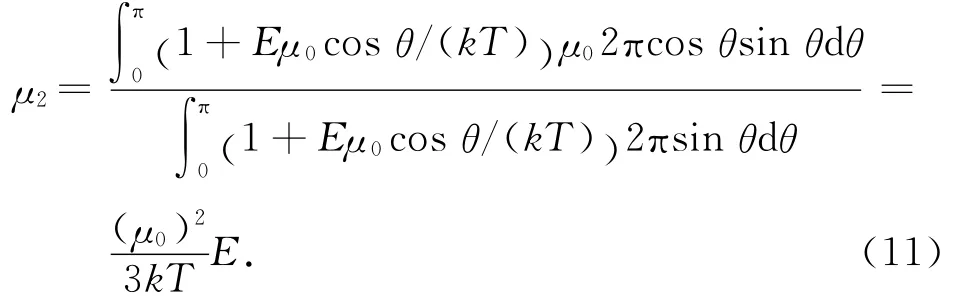
由式(11)可知:温度升高,取向偶极矩变小;温度下降,偶极矩变大。当取向偶极矩与温度成反比关系,若场强不变,温度上升使容量下降。从力学角度解释,温度上升,分子间无规则热运动加剧,使取向极化趋于无规则化,与外场强相反的力矩变小,容量变大。
电老练后,可通过将电容再放回烘箱一段时间后减小其取向极化强度,使容量恢复。
5 实验与分析
对CT41-2225-2C1-100V-225K,在温度(125±2)℃、电压200V、时间96h条件下老练,用HP4284对电老练前后的容量进行测试,结果见表1。由表1可知:老化后直接测试容量明显变小,放置24h后容量有所恢复,而损耗经老化后参数变小,且不易恢复。
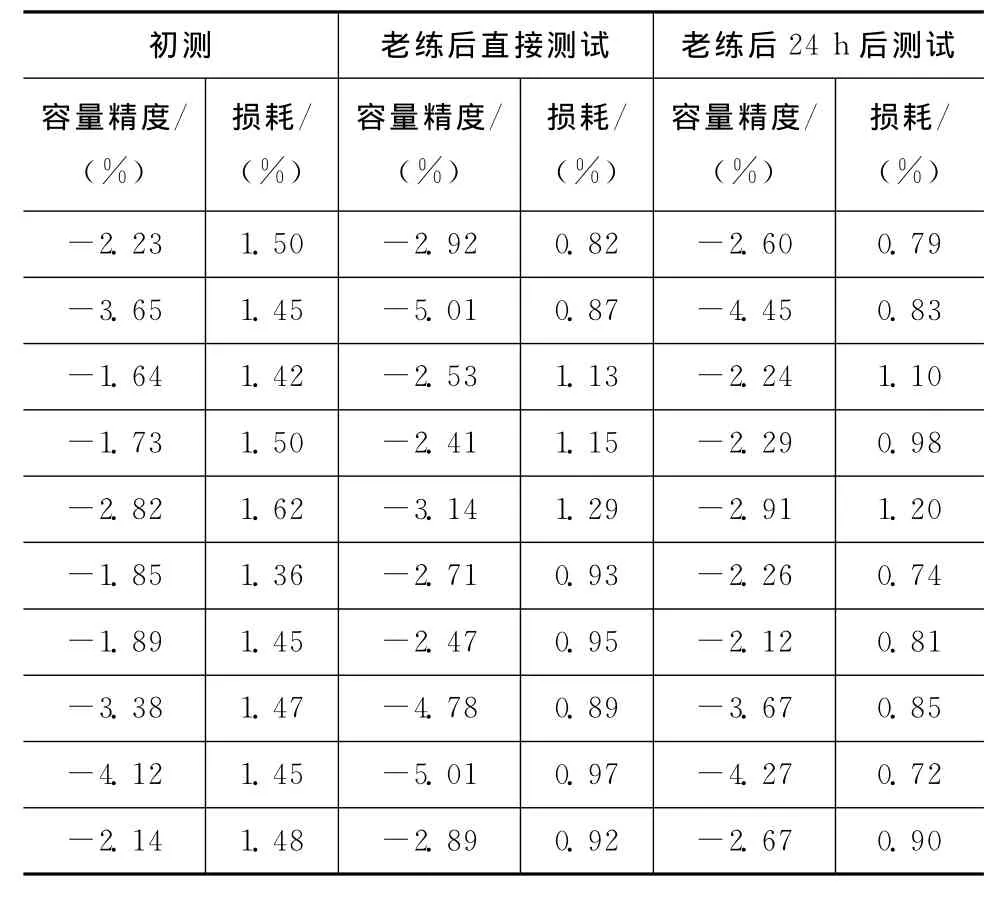
表1 CT41-2225-2C1-100V-225K试验数据Tab.1 Test data of CT41-2225-2C1-100V-225K
对 CC41-1210-CG-100V-301J,在 温 度 (125±2)℃、电压200V、时间96h条件下老练,用HP4284对电老练前后的容量进行测试,结果见表2。由表可知:老化后直接测试容量明显变小,放置24h后容量有所恢复,而损耗经老化后参数变化不大。
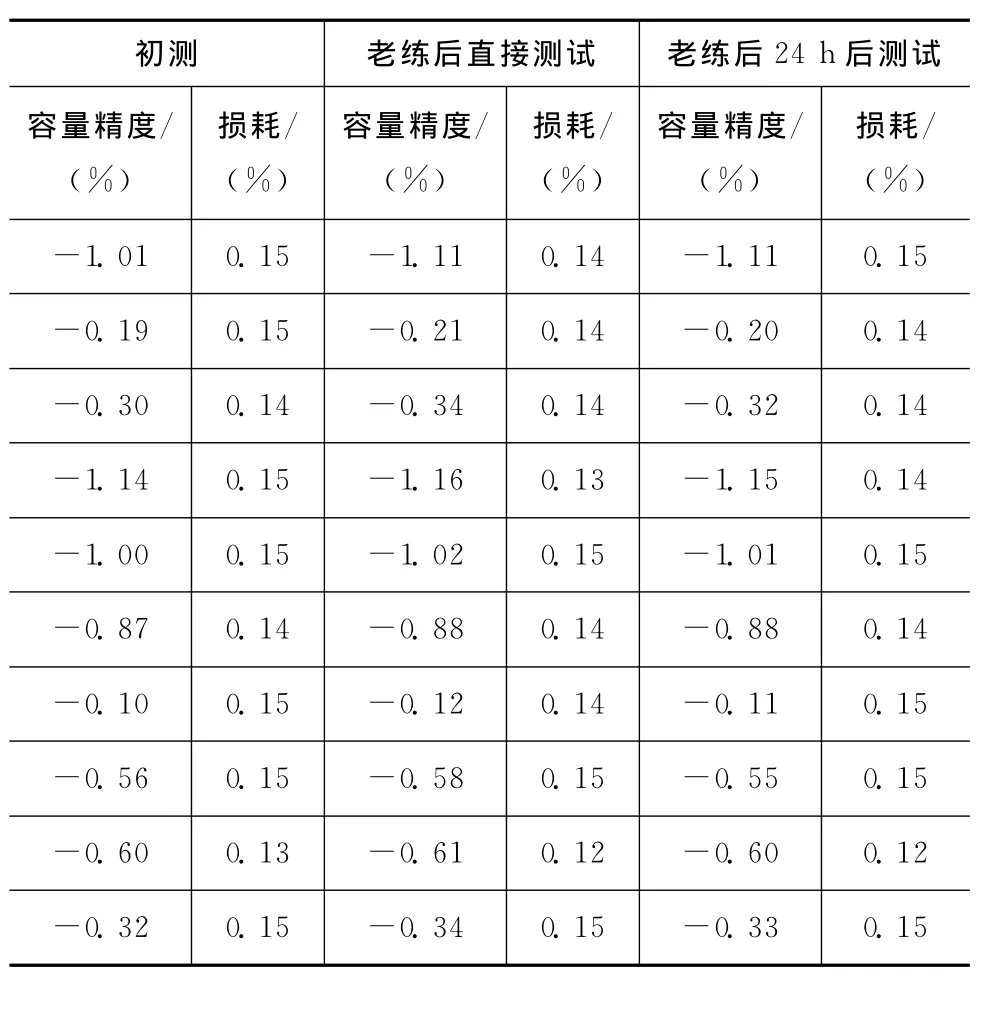
表2 CC41-1210-CG-100V-301J试验数据Tab.2 Test data of CC41-1210-CG-100V-301J
对C73-100V-0.1μF-G,在温度(85±2)℃,电压120V,时间96h条件下老练,用HP4284对电老练前后的容量进行测试,结果见表3。由表可知:老化后直接测试容量明显变小,放置24h后容量无明显恢复,经14d后明显恢复,而损耗经老化后,参数变小,需经较长时间恢复。由DPA试验发现其内部电极结构无明显异常,电极端并非导致容量变小原因,介质在高温、加压时产生变化,导致容量变化。

表3 C73-100V-0.1μF-G试验数据Tab.3 Test data of C73-100V-0.1μF-G
上述实验数据变化趋势证明理论定性分析正确,电老练后因电偶极子受老练电压和温度影响,电偶极矩增大,反向电荷密度增加,容量减小,损耗减小。可知二类瓷介电容器的稳定性较一类瓷介电容器的稳定性差,去老练应力需一定时间。长期试验结果表明:二类瓷介电容器需24h,也可将电容放回烘箱一段时间,效果较好。有机电容C73特性较不稳定,老练后测试需较长稳定时间,实际测试中老练后要2~3周才满足测试精度。国军标对电容去老练应力时间作了统一规定,没有区分瓷介电容、有机电容等,与实际测试试验不符。由于材料不同导致恢复时间不同,有机介质电容去应力时间至少为2周。
6 结束语
本文研究了电偶极子、电老练对电容参数的影响。电老练后,因电压与温度共同作用,介电常数发生变化,容量与损耗变小。不同种类的电容,因介质结构、特性各异,应制定不同的去应力时间以规范并便于测试操作:对瓷介电容去应力时间为24h,有机介质电容如C73(聚碳酸酯电容),其应力时间至少为2周;不能统一规定所有电容的去应力时间,应在对介质材料分析的基础上,规定老化去应力时间,也可在产品的详细规范或同类材料电容器的总规范中给出要求。
[1] 张三慧,臧庚媛,华基美.大学物理学 第3册.电磁学[M].北京:清华大学出版社,2008.
[2] 顾振军,王寿泰.聚合物的电性和磁性[M].上海:上海交通大学出版社,1990.
[3] 殷敬华,莫志深.现代高分子物理学[M].北京:科学出版社,2001.
[4] 盛 骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008.
[5] 张启仁.经典场论[M].北京:科学出版社,2001.
[6] 李正中.固体理论(第三版)[M].北京:高等教育出版社,2002.

