航天器可展附件展开动力学建模研究

孙宏丽，张少伟，谭天乐

（1.上海航天控制技术研究所，上海 201109；2.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

柔性多体系统动力学典型的应用是空间可展结构，如伸展臂、太阳帆板、可展天线等。为完成特定任务，航天器在空间环境中越来越多地使用了各种柔性外伸结构。为降低发射成本和增加有效载荷，这些柔性外伸结构有太阳能帆板、热辐射器、天线、柔性机械臂等，其共同特点是跨度大、结构质量轻、阻尼弱。空间环境振动轻则会影响航天器的正常工作，重则将导致整个航天器的失稳，因此航天器柔性外伸结构的振动控制历来是航天器设计中的重点和难点［1－3］。

航天器附件展开动力学的发展经历了从刚体模型到准刚体模型，从刚－弹－液耦合模型的演变过程。考虑柔性影响的航天器附件建模方法主要有集中参数法、假设模态法和有限元法三类［4］。研究主要包括展开结构的构成机理、展开运动特性、控制等。展开动力学分析是可展结构研究的重要领域，它可判定机构特性，并给出运动力学特性，对航天器可展附件在轨展开进行运动分析和动力学分析的意义重要。太阳能帆板和天线等可展结构的特点是尺寸大、质量轻、刚度低，固有频率很低且十分密集［5］。根据空间可展机构展开的力学状态，展开运动可分为主动态和被动态两种状态。主动态是指可展机构在马达或弹簧的作用下展开；被动态是指可展机构借助航天器的自旋实现展开。被动态使用较少，且运动状态有很大的不可控性，增加了其研究的复杂性，本文对航天器附件的主动态展开进行了研究。

1 多刚体模型的附件展开动力学

一卫星本体附带3个太阳能帆板的结构及简化的链式多体系统模型如图1所示。实践证明太阳能帆板展开时间不长且与卫星本体运动相互影响小，故多刚体模型近似认为在帆板展开过程中卫星本体绕质心作定点转动，仅需考虑本体的姿态与帆板运动的耦合［6－8］。

图1 太阳能帆板和多体系统结构Fig.1 Solar arrays structure and multibody system structure

因各刚体间为转动关铰或滑移铰，早期的研究多用D－H参数法和4×4齐次坐标变换理论进行运动学分析。文献［6］用D－H参数法和4×4齐次坐标变换理论对系统进行描述，并用Kane方法建立太阳能帆板的展开和碰撞动力学方程。

定义卫星本体的质心C0坐标系C0－xCyCzC与惯性参考系O－XYZ的齐次变换矩阵为AC，第i个刚体Bi上的连体基对O－XYZ系的齐次变换矩阵Ti＝ACA0A1…Ai，i＝1，2，…，n。此处：A0为卫星本体质心到本体坐标间的变换矩阵；Ai为卫星第i个附件至卫星本体坐标系的变换矩阵。设Bi的质心在本体坐标系的坐标列阵为rci＝［xciycizci1］T，是4×1列阵，最后一个数1表示该坐标列阵的比例关系。则Bi体在惯性参考系中的位置、速度、加速度分别为

式中：ωi为第i个体相对本体的角速度，且ωi＝A0A1…Ai；θj为第j个体关节角位移；Ωij＝∂ωi／∂θi；

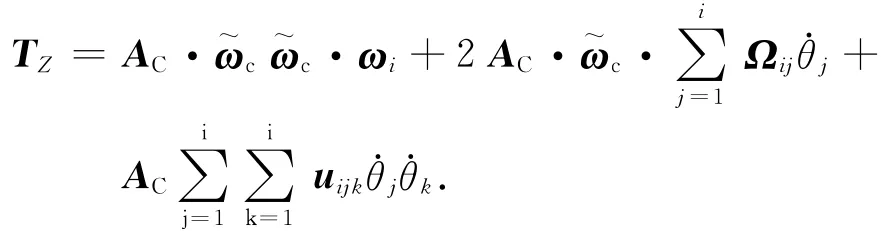
此处：uijk＝∂2ωi／（∂θi·∂θk）。Bi的角速度、角加速度矢量分别为

式中：nj－1为第j－1体连体基zj－1轴的单位方向矢量。

式中：i＝0，1，…，n；j＝1，2，…，n＋3。则对图1的模型，定义

式中：i＝1，2，3。

则系统的Kane动力学方程为

式中：r＝1，2，…，n＋3；Fr，分别为广义主动力和广义惯性力，且

式中：X为广义是（n＋3）×（n＋3）维的惯量阵；u为（n＋3）×1维的广义速率阵；f为（n＋3）×1维的广义力作用项及非线性项阵。

另须考虑展开终了时刻的碰撞。根据经典碰撞理论，碰撞发生在极短时间间隔Δt内物体位置不变，且有限值在Δt内积分为0，式（13）在Δt内积分为

式中：Kimpact为广义冲量，且

根据R／W方法可以写出图1所示结构的关联矩阵和通路矩阵分别为

取卫星本体质心C0为虚铰，则描述系统结构和位置的位形矩阵

式中：b1为本体质心至本体外铰点的位矢；b2，b3，b4分别为刚体1、2、3的内铰点至外铰点位矢；c1，c2，c3，c4分别为刚体1、2、3、4内铰点至质心的位矢。

各刚体Bi的连体基Ci－xiyizi的原点为质心Ci，Cizi轴与各铰的轴平行，各轴单位矢量如图2所示。整个系统有自由度10个，卫星本体的姿态用欧拉角描述，偏航角ψ，滚转角θ和仰俯角φ；连接架和各帆板的相对位置为α1，α2，α3。卫星本体的角速度

式中：p01，p02，p03为单位矢量，其与沿x、y、z方向的单位矢量i0，j0，k0的关系为

图2 各坐标系关系Fig.2 Relationship between each body

Bi体的角速度ωi，第1、2、3、4杆件局部坐标系中的角速度用ω1，ω2，ω3，ω4可表示为

式中：i＝1，2，3，4。因k0＝k1＝k2＝k3＝k4，则

设系统角速度列阵、角速度对角阵和各转轴单位矢量为元素的拟对角阵分别为

用广义速度表示的角速度列阵

［pH］T为转轴矩阵［p］与通路矩阵［T］的乘积，且［pH］T＝［p］［T］。引入对角阵

其元素是转轴矩阵中各转动单位矢量本身的角速度，因此有d［p］／dt＝［ωq］×［p］，则式（22）可表示为

式中：［H］为关联矩阵的逆，且［H］＝［S］T。角加速度列阵

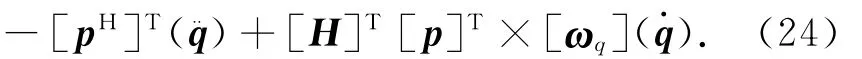
Bi体的外力主矢Fi和对质心的主矩Mi都等于0。各铰的扭簧力偶矩和摩擦力偶矩分别为

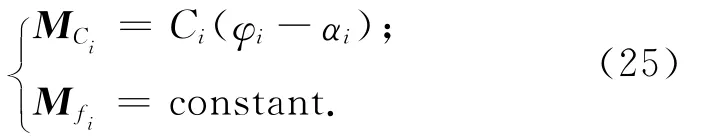
式中：Ci为Oi铰中扭簧的刚度系数；φi为扭簧的初始扭角；i＝1，2，3，4。总的内力偶矩Mi＝MCi－Mfi，铰的内力偶矩列阵

各刚体质量为元素，可得质量列阵（m）和质量对角阵［m］分别为

式中：m0为卫星本体质量；m1，m2，m3，m4分别为太阳支架和三块太阳帆板的质量。则系统总质量

定义对称质量阵

卫星本体的惯量张量

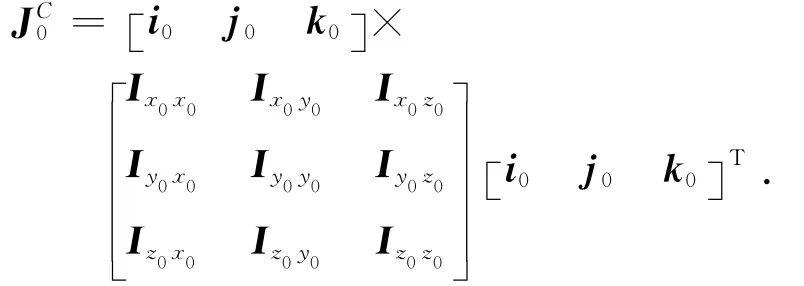
式中：Ix0x0，Iy0y0，Iz0z0分别为X、Y、Z向的主惯量阵；Ix0y0，Iy0z0，Ix0z0为惯量积。Bi体的中心惯量张量

则系统对卫星本体中心的惯量张量为对角阵

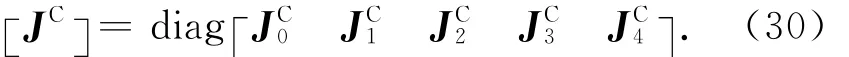
研究系统某个刚体的动力学时，其他刚体的质量几何参数的影响可用折算惯量张量表示，对整个系统，折算惯量张量可表示为

式中：Js为折算惯量张量；bc为各体质心至本体质心的距离；［E］为单位张量阵。［Js］是元素均为二阶张量的对称阵，则系统总惯量张量对称阵

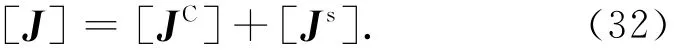
因仅考虑转动，系统动力学方程可表示为

式中：［Y］为铰链中阻尼和弹性力偶矩；

将式（32）代入式（27），令

整理可得含7个广义坐标

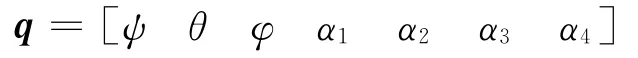
的二阶微分方程组

由于展开过程使用同步机构，α2＝α3＝α4＝2α1，系统增加约束方程3个，若只考虑转动，则系统的自由度降为4。

2 考虑柔性影响的展开动力学建模

柔性体本质上含无限多自由度，为适应计算机数值计算，须对柔性多体系统进行离散化，并用必要的截断以减少自由度数。离散化有对物理模型的离散和对数学模型的离散两类［8］。模态综合技术与有限元法结合，成为柔性多体系统离散化和建模的常用方法［9］。用假设模态法可将整个柔性体的变形场表示为一组模态函数（空间函数）和模态坐标（时间函数）的线性组合。通过模态分析，柔性体上任一点的变形位移列阵可表示为

式中：Φ为振型矩阵；q为模态坐标列阵。用有限元法可得较精确的位移表达。任意单元Ei内任一点p的变形位移为

式中：ρi，hi分别为Bi体的密度和厚度；，ap分别为点p相对惯性参考系O－XYZ的速度和加速度。

Bi体的广义惯性力和广义主动力列向量

Bi体的广义惯性力和结构弹性所对应的广义主动力

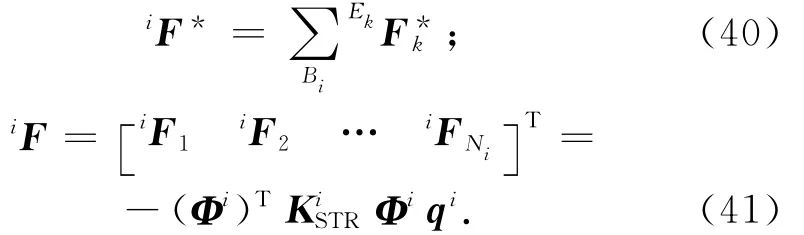
根据Kane方程，有

3 结束语

本文对对航天器附件的主动态展开进行了研究。基于柔性多体动力学理论，物理模型离散化采用有限元方法，用Kane方法建立柔性航天器可展开动力学模型。研究为一般构型刚柔耦合航天器的建模提供了参考，也为高精度航天器动力学快速自动生成模型提供了一种思路。

［1］ 陆佑方.柔性多体系统动力学［M］.北京：高等教育出版社，1996.

［2］ 洪嘉振.计算多体系统动力学［M］.北京：高等教育出版社，1999.

［3］ 洪嘉振，尤超蓝.刚柔耦合系统动力学研究进展［J］.动力学与控制学报，2004，2（2）：1－5.

［4］ 李 论.柔性机器人与机构动力学仿真的研究［D］.北京：北京工业大学，2000.

［5］ 杨 军.大型卫星太阳翼展开动力学研究［D］.哈尔滨：哈尔滨工业大学，2006.

［6］ HYLAND D C，JUNKINS J L，LONGMAN R W.Active control technology for large space structures［J］.Journal of Guidance，Control，and Dynamics，1993，16：801－821.

［7］ 黄文虎，王心清，张景绘，等.航天柔性结构振动控制的若干新进展［J］.力学进展，1997，27（1）：5－18.

［8］ 李东旭.空间结构的动应变控制［J］.国防科技大学学报，2000，22（4）：9－11.

［9］ 何柏岩，王树新.航天器帆板展开过程动力学建模与仿真［J］.计算机辅助设计与图形学学报，2006，18（2）：319－323.