基于AMESim减压阀动态特性仿真与试验研究

滕 浩，石玉鹏，张 亮，臧 辉

（上海宇航系统工程研究所，上海 201109）

0 引言

减压阀是运载火箭氦增压系统中的关键单机。在减压阀研制过程中，出现了－40℃低温条件下出口压力剧烈振荡以及启动段压力长时间下降的问题。出口压力的剧烈振荡会影响增压输送系统增压，严重时可导致火箭发射失败。文献［1］对大流量减压阀在增压过程中出现的压力剧烈振荡问题建立了非稳态模型并进行数值计算，研究了减压阀的振荡特性。文献［2］针对高压气动减压阀，建立了考虑泄漏影响的数学模型，分析了泄漏对减压阀压力响应的影响。文献［3］将摩擦力等非线性因素引入减压阀动态特性分析中，建立了气体减压阀动态数学模型，分析了摩擦力的存在对阀芯迟滞效应的影响。这些研究主要针对减压阀起动及稳态工作特性的分析，但对因变流量泄漏及摩擦力的存在对整个增压过程压力振荡的动态分析较少涉及。本文考虑减压阀工作过程中存在摩擦力、泄漏、阻尼、起动冲击、负载突变等影响减压阀动态性能的因素，对减压阀的动态响应特性进行了研究。

1 减压阀结构原理

减压阀结构如图1所示。活门（序号2）与壳体（序号1）间形成环形节流口，节流口开度为h。高压气体从入口进入高压腔，经节流口后减压至设定的低压压力，低压腔的低压气体通过阻尼孔的滤波作用进入反馈腔。减压阀的活动部件在入口高压气体作用力F1、减压后的低压气体作用力F2、反馈腔低压气体作用力F3、弹簧作用力Fs、环境大气作用力Fa，以及阀芯动作过程所受摩擦力Ff、阻尼等的共同作用下处于动态平衡。在出现外界干扰（入口压力、流量负载发生变化）时，减压阀在平衡力的作用下h可作相应的调整，使出口压力保持稳定。

图1 减压阀结构Fig.1 Schematic of pressure relief valve

2 减压阀动态特性仿真数学模型

2.1 气体流量模型

在减压阀系统计算时，假定气体为理想气体，气体整个流动过程分为声速流和亚声速流，则体流量

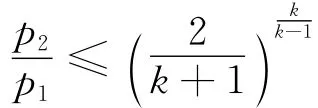
式中：μ为流量系数；A为流体流动截面面积；p1，p2分别为入口、出口压力；T1为入口温度；k为介质绝热指数；Rg为气体常数。

2.2 摩擦力模型

仿真过程中，考虑阀芯所受摩擦力对减压阀性能的影响，摩擦力模型采用工程常用的SCV模型：静摩擦力＋库仑摩擦力＋黏性摩擦力模型（Static＋Coulomb＋Viscous）。物体从静止开始加速，摩擦力经历了弹性变形、边界润滑、部分流体润滑和全流体润滑四个阶段。Stribeck曲线可反映摩擦力经历的弹性变形（Ⅰ）、边界润滑（Ⅱ）、部分流体润滑（Ⅲ）和全体流体润滑（Ⅳ）四个阶段，即滑动速度和摩擦力的关系（如图2所示），Stribeck摩擦力模型可表示为

式中：Fa为施加外力；Fs为静摩擦力；v为滑动速度；s（v）为Stribeck曲线函数［4］。根据应用场合，s（v）有不同的表述方式，其中最普遍是

与此同时，质疑静态大陆的观点开始流行起来。对于开始接触这一理论的人来说，魏格纳的非正统思想引发了一些重大问题，如什么力量可以导致大陆在海洋上滑行？这些问题又引发了新理论：泛大陆分离开来是因为地球正在变得越来越大。

式中：fv为摩擦因数；x为运动位移；t为运动时间；Fc为库伦摩擦力；vs为 Stribeck速度；δvs用于控制 Stribeck曲线形状；η为黏性摩擦因数［5－6］。

图2 摩擦力与滑动速度间关系（Stribeck模型）Fig.2 Relationship between friction and velocity（Stribeck model）

2.3 质量系统动态模型

对图1所示减压阀，在动态调节过程中，作用于阀芯、活门等运动部件上的力有F1，F2，F3，Fs，Fa，Ff，此外还有阻尼力及流体流动作用力等非线性因素。分析运动组件受力，其运动系统的动态方程可表示为

式中：Ff·l为流体流动作用力，且

m∑为运动件总质量；x为阀芯位移；p1为高压腔压力；A1为高压力作用面积；p2为低压腔压力；A2为低压力作用面积；p3为反馈腔压力；A3为反馈压力作用面积；F0为弹簧预紧力；k为弹簧刚度；Cu1为节流口流量系数；T1为入口气体温度；qm1为入口气体流量；φ为气体流动函数；θ为阀座凸角；T2为出口气体温度；qm2为出口气体流量；L为阻尼长度［7］。

减压阀阀芯等运动部件与弹簧组成弹簧振子，在外力作用下作阻尼振动，其振动方程为

2.4 能量模型

对减压阀工作系统，考虑气体流进流出的能量交换及与外界环境的热交换，在dt时间内进入系统质量为δm1，流出系统质量为δm2，系统与外界环境换热δQ，对外做功δWi，则减压阀试验系统工作过程的能量方程为

式中：δECV为控制容积内总能的增量；h1，h2分别为进出口气体比焓；cf1，cf2分别为进出口气体流速；z1，z2分别为进出口气体位置高度；δWi为内部功［9］。

3 减压阀试验系统动态仿真模型

建立减压阀试验系统如图3所示，用AMESim仿真工具建立减压阀试验系统动态特性仿真模型。模型中，减压阀、管路结构尺寸均按实测值给定。仿真模型构建中，考虑阀芯的力学和气体的流动模型。关键是确定作用于阀芯上的力：弹簧作用力、高低压及反馈三个腔室气体作用力、摩擦力。气体流动模型考虑了系统与环境的换热以及内漏、容腔的容性和阻尼孔、缝隙流的阻性等对减压阀性能的影响。此外，模型作以下简化：压缩高压气体为理想气体；仿真模型为零维模型，对高压腔、低压腔、反馈腔等独立腔室，忽略因气体流动带来的压力、温度分布不均的影响；电磁阀忽略起动关闭响应特性，简化为瞬间打开关闭。

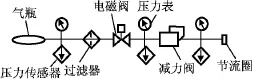
图3 减压阀试验系统Fig.3 Experimental system of pressure relief valve

4 减压阀仿真试验

4.1 动态仿真与试验结果

图4 低温条件出口压力试验结果Fig.4 Experimental results of outlet pressure at low temperature

减压阀出口压力仿真结果如图5所示。仿真中考虑了低温条件下高压密封失效，高压腔气体泄漏至反馈腔的情况，并采用了Stribeck摩擦力模型，研究摩擦力对减压阀性能的影响。与图4比较后发现：电磁阀打开后，出口压力均出现起动冲击，冲高至约3.1MPa；压力波动的趋势基本一致，即初始阶段气瓶压力高时波动剧烈，随着气瓶压力的降低，出口压力趋于稳定；在220～360s间出现压力升高后缓慢下降的爬行现象；末段稳定值基本一致（约2.5MPa）；波动的幅值约1.3MPa，与试验数据波动幅值（1.2MPa）较接近。仿真与试验曲线基本一致，表明仿真模型构建正确。

图5 高压泄漏仿真压力结果Fig.5 Simulated results of outlet pressure when leakage at high pressure

4.2 减压阀性能影响因素

仿真模型中减压阀初始最大开度h0按实际结构为0.65mm，并确定h0在零位（x＝0），h减小方向为x正向。

4.2.1 高压密封内漏

由图1，活门与壳体为间隙配合，定义配合间隙的环缝面积为A，减压阀高压腔与反馈腔通过密封圈隔离，在低温－40℃条件下若密封圈收缩，会导致高压腔的高压气体将通过密封圈泄漏至反馈腔。

泄漏面积分别为0.06A，0A（无泄漏）时的出口压力仿真结果如图6所示。由图6可知：当泄漏面积稳定时，出口压力较无泄漏时偏高，但无波动现象。

图6 泄漏面积0.06A，0A时出口压力仿真结果Fig.6 Simulation results of outlet pressure with leakage area 0.06Aand 0A

高压密封圈泄漏面积为0A～0.06A时出口压力仿真结果如图7所示。由图可知：出口压力出现波动，且随着气瓶压力降低，泄漏流量减小，导致压力波动减小并最终稳定，与图5波动规律一致。

4.2.2 摩擦力

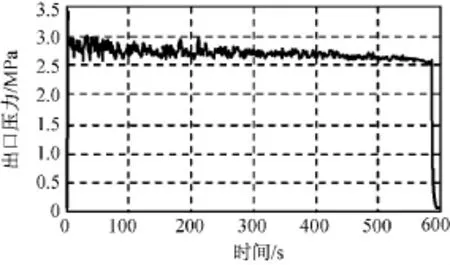
图7 泄漏面积为0A～0.06A时出口压力仿真结果Fig.7 Simulation results of outlet pressure when leakage area between 0Aand 0.06A

取减压阀产品实测值Ff＝10N，考虑阻尼系数β的影响，减压阀出口压力仿真结果如图8所示。由图可知：0s电磁阀打开后减压阀开始工作，出口压力冲高至约3.5MPa后迅速回落至3.0MPa；在初始66s内减压阀出口压力单调下降，不能保持稳定；在66s后减压阀出口压力稳定在约2.6MPa。阀芯位移结果如图9所示。由图可知：起动时阀芯位移冲击至0.650mm后迅速回至0.573mm处，并保持稳定不变，减压阀处于固定节流状态，失去了压力调节能力，导致减压阀出口压力单调下降；在66s后，随着气瓶压力的下降，阀芯所受的不平衡力大于摩擦力的影响，减压阀h＝h0－x开始随气瓶压力的降低而增大，减压阀处于动态平衡调节状态，出口压力稳定。

图8 摩擦力10N、阻尼系数不为零时出口压力仿真结果Fig.8 Simulation results of outlet pressure with friction 10Nand damp coefficient not zero

不考虑摩擦力，令Ff＝0N，考虑β的影响，减压阀出口压力和阀芯位移仿真结果分别如图10、11所示。与图8比较后发现：带摩擦力状态，初始段无压力单调下降现象，整个工作过程压力保持稳定在2.7MPa，表明摩擦力的存在是导致该减压阀初始压力单调下降的一个重要因素。与图9比较后发现：减压阀起动后阀芯位移达到0.578mm后无停滞，减压阀阀芯处于动态平衡调节状态，出口压力稳定。

图9 摩擦力10N、阻尼系数不为零时阀芯位移仿真结果Fig.9 Simulation results of displacement of piston with friction 10Nand damp coefficient not zero

图10 摩擦力为0N、阻尼系数不为零时出口压力仿真结果Fig.10 Simulation results of outlet pressure with friction 0Nand damp coefficient not zero

不考虑摩擦力和阻尼的影响，令Ff＝0N，β＝0N／（m·s－1），减压阀出口压力仿真结果如图12所示，阀芯位移如图13所示。与图11比较发现：在减压阀阀芯的动作失去阻尼约束后，工作过程中会导致阀芯在平衡位置附近出现剧烈振荡，但出口压力能保持稳定，且无起动冲击。

因运动部件受摩擦力和阻尼作用的影响，在外界干扰条件下引起摩擦自激振动产生爬行，爬行与动、静摩擦力之差、运动件是否处于摩擦力降落特性区域、有无能量贮存与释放及惯性等因素有关［10］。减压阀由于泄漏原因，对运动部件产生的不平衡力的扰动，会导致阀芯在工作过程中处于间歇性停滞状态。减压阀出口压力爬行仿真结果如图14所示，阀芯位移仿真结果如图15所示。

图11 摩擦力为0N、阻尼系数不为零时阀芯位移仿真结果Fig.11 Simulation results of displacement of piston with friction 0Nand damp coefficient not zero

图12 摩擦力为0N、阻尼系数为0N／（m·s－1）时减压阀出口压力仿真结果Fig.12 Simulation results of outlet pressure with friction 0N and damp coefficient 0N／（m·s－1）

5 减压阀改进设计

由减压阀动态特性仿真结果，可得以下结论。

a）减压阀仿真压力与试验较一致，表明本文建立的减压阀动态仿真系统模型符合实际，满足工程使用需求。

b）减压阀低温条件下压力剧烈波动是因为减压阀高压密封圈在低温条件下失效，导致高压腔的高压气体泄漏至反馈腔，且随气瓶压力降低，泄漏量降低后，减压阀出口压力趋于稳定。

图13 摩擦力为0N，阻尼系数为0N／（m／s）时减压阀阀芯位移仿真曲线Fig.13 Simulation results of displacement of piston with friction 0Nand damp coefficient 0N／（m·s－1）

图14 有爬行时出口压力仿真结果Fig.14 Simulation result of outlet pressure with stick－slip phenomenon

图15 有爬行时阀芯位移仿真结果Fig.15 Simulation result of displacement of piston with stick－slip phenomenon

c）可认为减压阀初始阶段压力持续下降及出口压力的爬行是由外界干扰导致摩擦力的波动，阀芯在不同的平衡位置出现了间歇性停滞状态，减压阀失去调节能力，处于固定节流状态。

综合有，现阶段产品低温环境中出现压力剧烈波动的原因是由于高压密封圈收缩出现泄漏，且泄漏过程不均匀引起摩擦力发生不规则变化，导致出现压力上升后缓慢下降的爬行。因此，可改进高压密封结构设计，在保证密封的前提下尽量减小摩擦力。产品改进设计后减压阀出口及低温条件下压力的试验结果分别如图16、17所示。由图可知：减压阀在低温不漏情况下，出口压力在初始阶段因摩擦力不能稳定。与设计更改前的图5相比，改进后出口压力稳定，无剧烈波动。

图16 更改设计后减压阀出口压力仿真结果Fig.16 Simulation result of outlet pressure after optimal design

图17 更改设计后低温条件下减压阀出口压力试验结果Fig.17 Experimental result of outlet pressure after optimal design

6 结束语

本文对基于AMESim减压阀动态特性进行了研究。通过减压阀动态特性仿真分析，建立了试验系统的仿真模型，仿真结果较为真实反映产品的性能，通过减压阀性能影响参数仿真分析，优化了产品的结构参数，缩短了研制周期，节省了研制费用。

［1］ 谭建国，江燕平，王振国.减压器增压过程中的振荡抑制措施［J］.推进技术，2013，34（1）：124－128.

［2］ 徐志鹏，王宣银，罗语溪.滑阀先导式高压气动减压阀间隙泄漏特性研究［J］.浙江大学学报（工学版），2009，43（10）：1789－1793.

［3］ GAD O.Comprehensive nonlinear modeling of a pilot operated relief valvea［J］.Journal of Dynamic Systems，Measurement and Control，2013，135（1）：011011－1－7.

［4］ 张新刚.基于扩展Stribeck效应的摩擦实验建模及系统动力学研究［D］.上海：上海交通大学，2009.

［5］ BO L C，PAVELESCU D.The friction－speed relation and its influence on the critical velocity of the stick－slip motion［J］.Wear，1982，82（3）：277－289.

［6］ ARMSTRONG－HELOUVRY B.Control of machines with friction［M］.Boston：Kluwer Academic Publishers，1991.

［7］ 尤裕荣，曾维亮.逆向卸荷式气体减压阀的动态特性仿真［J］.火箭推进，2006，32（3）：24－30.

［8］ 航空机械设计手册编辑组.航空机械设计手册［M］.北京：国防工业出版社，1975.

［9］ 沈维道，蒋智敏，童钧耕.工程热力学（第三版）［M］.北京：高等教育出版社，2001.

［10］ 任卫红.摩擦自激引起的液压爬行现象分析［J］.煤矿机械，2003（10）：43－45.