空间杆状构架式展开机构拓扑型综合与分析

李 波，陈晓峰

（上海宇航系统工程研究所，上海 201109）

0 引言

空间杆状构架式展开机构作为航天器大型支撑机构，具有重要的支撑定位功能，可实现空间有效载荷的长距离、大面积展开。空间杆状构架式展开机构主要由可折叠的复杂杆系组成，具有质量小、收藏比大、比刚度高、可靠性高等特点，可较好地解决运载整流罩的包络空间有限对航天器空间构型的制约问题，能满足航天器发射和在轨不同阶段的任务需求，是一种典型的空间变胞机构，在空间技术领域有重要的研究价值和广阔的应用前景［1－4］。

机构综合与机构分析是机构学研究的两个基本内容。机构综合着重创造性构思、发明、创新设计新机构的理论与方法的研究；机构分析着重机构结构学、运动学及动力学特性的研究，揭示机构结构组成、运动学与动力学规律及其相互联系，用于现有机构性能分析与改进，同时为机构综合提供理论依据［5］。机构综合又包括型综合和尺寸综合两个方面，其中型综合是指确定最适于问题的机构类型。目前，机构的型综合与分析是通过计算机辅助设计及其辅助分析软件完成的。因这两类软件分属不同的工作平台，机构分析时设计人员常采用传统分析方法，即先由计算机辅助设计软件给出机构类型，再采用计算机辅助分析软件输入机构必要的参数，对机构的各项性能进行分析和评估，这样增加了中间环节，降低了工作效率。为此，本文应用拓扑理论在同一平台上对机构的型综合与结构分析进行了研究。

1 杆状构架式展开机构型综合

式中：n为运动链构件数（即拓扑图顶点数）；m为运动副数（即拓扑图边数）；ni为具i个运动副的构件数，i＝1，2，3，…，该构件称为i副杆或i元杆。

由图论和欧拉方程式，有

式中：ν为拓扑图基本回路数。

满足式（1）、（4）的n，m，ν组合有无穷多解，即运动链有无穷多。根据拓扑结构要求，选取三回路进行构型综合，则有n＝10，m＝12，ν＝3。由式（2）、（3）可知

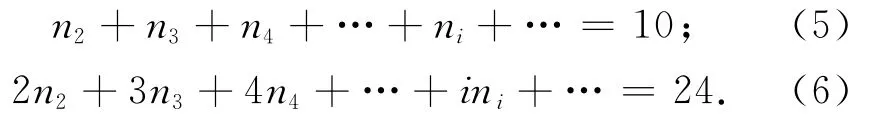
将式（5）、（6）代入式（1），得

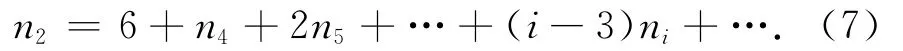
由式（5）、（7）可得十杆机构的结构方案如下。

a）方案Ⅰ：n2＝6，n3＝4。

b）方案Ⅱ：n2＝7，n3＝2，n4＝1。

第五，为了充实实验的全面性，建议在山区对各像控点布设方案做更多的实验，同时也可以适当改变基线相隔数量以及航带相隔数量并分别验证其精度。

c）方案Ⅲ：n2＝8，n4＝2。

选用方案Ⅲ作为运动链的基本结构形式，对应的拓扑胚图类型如图1所示。图中，多副杆（i≥3）用顶点表示，顶点用边连接，每条边代表一支由二副杆组成的运动链。采用运动链拓扑胚图插点法，在胚图的边中插入n2构件，不同分配方式，可得各种异构体（或称异构运动链）。为便于区别，用4个数字表示4支运动链中二副杆的构件数，由此可得两种异构体，如图1所示。

对各种异构体，按平面运动副同一级别间可相互转换，不同级别按高副低代的原则，确定可行的机构组成。则由异构体3212得到的运动链如图2所示，相应的机构如图3所示。

2 杆状构架式展开机构展开过程型综合

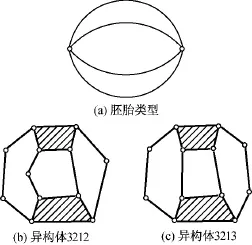
图1 方案Ⅲ对应的胚图类型及异构体Fig.1 Contracted and isomers for schemeⅢ

图2 三自由度十杆机构运动链Fig.2 Kinematical chain of a ten－bar mechanism with 3DOFs

图3 三回路十杆构架式展开机构结构Fig.3 A ten－bar mechanism with 3loops

变胞机构与传统机构的不同之处是机构在构态变化的过程中自由度发生变化。自由度的变化取决于机构运动链及拓扑结构的变化，该类机构结构变化由构件的合并引起，具体表现为构件和运动副数的变化。按自由度的变化规律，变胞机构可分为三类：第一类，自由度逐渐由多到少；第二类，自由度逐渐由少到多；第三类，上述两者混合变化，即有时自由度逐渐增加，有时自由度逐渐减少［6］。

空间构架式展开机构属于第一类变胞机构，其展开过程的型综合实质是变胞机构的型综合。在展开的最初阶段，杆系折叠收拢在航天器侧壁，杆件间通过铰链连接，各铰链均处于活动状态（如图3（a）所示），机构为三自由度杆系，此时对应为机构的始态。展开过程中，在控制系统和锁定装置的作用下，杆系各铰链依次锁定，展开到位后整个杆系形成一稳态结构，自由度变为0，此时对应为机构的终态。

根据展开机构自由度变化的特点，为实现机构构态变化前后自由度减少1，应满足关系

式中：n，n′分别为构态变化前后的构件数；m，m′分别为构态变化前后的运动低副数。

因n，n′，m，m′必须为正整数，故满足上述条件且符合实际情况的组合有

式（9）、（10）表明：机构实现自由度减少1具有以下变化规律和结构特点：

a）将相邻接的两构件合并，构件和运动副各减少1个；

b）将同一回路中相隔2个构件的两构件合并，减少构件3个和运动副4个。

根据展开机构的工作特性，在运动过程中其自由度从3→2→1→0。按上述变化规律，只要将任意相邻接的两构件合并即可得自由度为2的运动链，有“1、2”，“2、3”，“3、4”，“4、5”，“5、6”，“6、7”，“7、1”，“2、8”，“5、8”，“2、9”，“9、10”，“5、10”杆件合并共12种形式，消除同构体（即同构运动链）后得到3种异构体方案如图4所示。

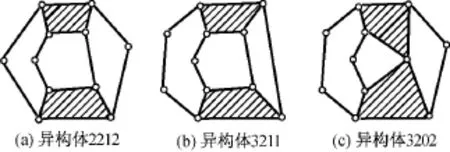
图4 自由度由3变2的异构体方案Fig.4 Isomers with 2DOFs

同理，由异构体3211可综合出实现自由度从2→1→0的运动链方案，如图5所示。

图5 自由度由2变0的运动链Fig.5 Kinematical chain of DOF changing

3 杆状构架式展开机构型分析

机构的型分析是机构学研究中重要方面，为机构的选型和应用提供相应的评价准则。根据构架式展开机构的工作特性不仅可综合出工作周期内构态的变化过程，还能得到机构的拓扑特性矩阵，作为定量评价机构性能的工具。

机构的距离矩阵D和刚度矩阵S分别描述了该构型展开机构的空间紧凑性和整体刚度。利用这些拓扑矩阵，便于在方案阶段快速、合理地分析和选择杆系构型。

3.1 距离矩阵

紧凑性是反映机构静态性能的一个重要指标。机构越紧凑表明其静态性能越好，并占有较小的空间。在不考虑杆件尺寸的情况下，杆件和运动副数越少的机构越紧凑，具有相同杆件和运动副数的不同设计构型的机构，其空间紧凑性通过定义杆件之间的距离描述，用距离矩阵D表示。D越小，机构越紧凑。

图1中，运动链3212及其对应机构的距离矩阵分别为

静态距离矩阵为一n×n阶对称矩阵，此处n为描述机构的构件数。矩阵中的元素dij代表了机构中第i，j个构件间最少的运动副数，且当i＝j时，dij＝0［7］。矩阵Dc中所有元素之和为距离值。因此，构型3212方案中，机构的距离值为182；构型3113方案中，机构的距离值为192，可见对应具有相同杆件和运动副数的上述两种构型，构型3212方案空间布局更紧凑。

3.2 刚度矩阵

机构的实际刚度由杆件尺寸、弹性及支撑决定。在不考虑杆件物理参数和几何参数的前提下，杆系刚度取决于各杆件的支撑点数，每个杆件的支撑点数为该杆的连通度，机构的刚度用S表示。

图1中，运动链3212，3113对应机构的刚度矩阵

式中：S3212中，s11＝2，s12＝4，s13＝4／3，s14＝4／5，s15＝4／5，s16＝1，s17＝2，s18＝4／3，s19＝4／3，s110＝4／5，s21＝2，s22＝4，s23＝2，s24＝1，s25＝4／3，s26＝2／3，s27＝1，s28＝2，s29＝2，s210＝1，s31＝4／3，s32＝4，s33＝2，s34＝2，s35＝4／3，s36＝4／5，s37＝4／5，s38＝4／3，s39＝4／3，s310＝4／5，s41＝4／5，s42＝4／3，s43＝2，s44＝2，s45＝4，s46＝4／3，s47＝4／5，s48＝4／3，s49＝4／5，s410＝4／3，s51＝2／3，s52＝4／3，s53＝1，s54＝2，s55＝4，s56＝2，s57＝1，s58＝2，s59＝1，s510＝2，s61＝1，s62＝4／5，s63＝4／5，s64＝4／3，s65＝4，s66＝2，s67＝2，s68＝4／3，s69＝4／5，s610＝4／3，s71＝2，s72＝4／3，s73＝4／5，s74＝4／5，s75＝4／3，s76＝2，s77＝2，s78＝4／5，s79＝4／5，s710＝4／5，s81＝4／3，s82＝4，s83＝4／3，s84＝4／3，s85＝4，s86＝4／3，s87＝4／5，s88＝2，s89＝4／3，s810＝4／3，s91＝4／3，s92＝4，s93＝4／3，s94＝4／5，s95＝4／3，s96＝4／5，s97＝4／5，s98＝4／3，s99＝2，s910＝2，s101＝4／5，s102＝4／3，s103＝4／5，s104＝4／3，s105＝4，s106＝4／3，s107＝4／5，s108＝4／3，s109＝2，s1010＝2；S3213中，s11＝2，s12＝4，s13＝4／3，s14＝4／5，s15＝1，s16＝2，s17＝4／3，s18＝4／3，s19＝4／5，s110＝4／7，s21＝2，s22＝4，s23＝2，s24＝4／3，s25＝2／3，s26＝1，s27＝2，s28＝2，s29＝1，s210＝2／3，s31＝4／3，s32＝4，s33＝2，s34＝4，s35＝4／3，s36＝4／5，s37＝4／3，s38＝4／3，s39＝4／5，s310＝4／3，s41＝2／3，s42＝4／3，s43＝2，s44＝4，s45＝2，s46＝1，s47＝2，s48＝2／3，s49＝1，s410＝2，s51＝1，s52＝4／5，s53＝4／3，s54＝4，s55＝2，s56＝2，s57＝4／3，s58＝4／7，s59＝4／5，s510＝4／3，s61＝2，s62＝4／3，s63＝4／5，s64＝4／3，s65＝2，s66＝2，s47＝4／5，s48＝4／5，s49＝4／7，s410＝4／5，s71＝4／3，s72＝4，s73＝4／3，s74＝4，s75＝4／3，s76＝4／5，s77＝2，s78＝4／3，s79＝4／5，s710＝4／3，s81＝4／3，s82＝4，s83＝4／3，s84＝4／5，s85＝4／7，s86＝4／5，s87＝4／3，s88＝2，s89＝2，s810＝1，s91＝4／5，s92＝4／3，s93＝4／5，s94＝4／3，s95＝4／5，s96＝4／7，s97＝4／5，s98＝2，s99＝2，s910＝2，s101＝4／7，s102＝4／5，s103＝4／3，s104＝4，s105＝4／3，s106＝4／5，s107＝4／3，s108＝1，s109＝2，s1010＝2。

其中，矩阵中元素

式中：Ci，Ck，Cj为不同杆件的连通度（每个杆件的运动副数）。当i＝j时，刚度矩阵的元素值就是杆件自身的连通度。当i≠j时，刚度矩阵的元素值是除杆件i外，从杆件i到杆件j经过的最短路径中所有串联杆件连通度的运算之和。如存在多条最短路径，则应选取由具有最小连通度的杆件组成的最短路径。刚度矩阵中的每一行元素之和代表了该行对应杆件的刚度，所有元素之和代表了整个机构的刚度。因此，构型3212方案中杆件1～10的刚度值依次为 77／5，17，236／15，236／15，17，77／5，38／3，94／5，236／15，236／15，总体刚度值159.2；构型3113方案中杆件1～10的刚度值为531／35，50／3，274／15，50／3，531／35，1 306／105，274／15，531／35，1 306／105，531／35，总体刚度值155.43。由此可见，对应具有相同杆件和运动副数的上述两种构型，构型3212方案整体刚度更强。

4 结束语

根据空间杆状构架式展开机构的工作特性，本文应用拓扑理论研究了运动链结构的变化及其对应构型下的拓扑特性矩阵，为在同一平台上进行变自由度机构的综合、选型和应用提供了手段。本文研究的型分析方法简洁、实用，利用矩阵运算分析并对比了不同运动链的结构特征和拓扑性能，得到了最佳的运动链构型方案，对空间杆系结构布局的优化具有一定的指导意义。因将型分析问题转化为矩阵运算，本文提出的方法易于在计算机上进行，对开发变胞机构快速设计系统，实现空间机构系统设计与分析一体化有重要作用。

［1］ 李瑞玲，戴建生，张启先，等.基于构态变换的变胞机构结构综合［J］.机械工程学报，2002，38（7）：12－16.

［2］ 金国光，高 峰，丁希伦.变胞机构的分类及其构态分析［J］.机械科学与技术，2005，24（7）：764－767.

［3］ 王徳伦，戴建生.变胞机构及其综合的理论基础［J］.机械工程学报，2007，43（8）：32－42.

［4］ 李东福，金国光，吴艳荣.变胞机构理论和应用研究概述［J］.机械科学与技术，2007，26（2）：227－230.

［5］ 杨廷力.机械系统基本理论－结构学·运动学·动力学［M］.北京：机械工业出版社，1996.

［6］ 郭宗和，马履中，杨启志.基于变胞原理的变自由度机构拓扑型分析［J］.中国机械工程，2005，16（1）：1－3.

［7］ RAO A C.Topological characteristics of linkage mechanisms with particular reference to platform－type robots［J］.Mechanism and Machine Theory，1995，30（1）：33－42.