火箭三级无动力飞行段晃动的一种建模方法

修 观，李 鑫

（上海宇航系统工程研究所，上海 201109）

0 引言

对液体推进剂运载火箭，箭体运动引起的推进剂相对箭体的运动被称为推进剂晃动。推进剂晃动与箭体姿态运动间的耦合是通过惯性力的相互作用产生的。当晃动不稳定时，晃动幅值不断增大，火箭姿态角会随晃动惯性力作用增大而加大，从而导致箭体姿态运动发散。因此，设计姿态控制系统时必须保证推进剂晃动的稳定性。为了解和掌握推进剂晃动规律，对液体晃动进行了大量试验和理论研究，假设液体为不可压缩和无旋，建立了描述液体晃动的等效力学模型。其中单摆和等效弹簧－质量两种模型应用广泛，且后者尤为国内所常用［1－4］。文献［1－2］用单摆模型描述飞行器液体晃动，且文献［2］采用动态逆控制抑制晃动；文献［3－4］用等效弹簧－质量模型描述飞行器液体晃动，文献［3］对飞行器晃动稳定性进行了研究，认为液体晃动与重力无关，成果显著。

在某液体运载火箭三级无动力飞行段姿态控制系统设计中，发现偏航通道在晃动频率附近，相位严重滞后，晃动不稳定；俯仰通道晃动相位超前，晃动稳定。从同型号液体运载火箭飞行试验数据中，还发现了三级无动力飞行段存在偏航姿态角超差。为解决工程实际中的晃动不稳定和姿态角超差，本文对一种新的液体晃动方程的建立进行了研究。

1 晃动不稳定与姿态角超差现象

某液体运载火箭的三级采用共底贮箱，各贮箱加装十字或米字形隔板，提高晃动阻尼和晃动频率，抑制液体晃动。在无动力飞行段姿态控制系统设计中，偏航通道在晃动频率附近，相位滞后约180°，晃动不稳定，系统设计难度很大；俯仰通道晃动相位超前，晃动稳定，系统设计较易。设计中，俯仰通道和偏航通道采用的原有的液体晃动方程形式上相似，俯仰和偏航通道晃动方程分别为

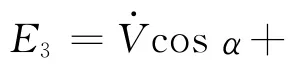
分析表明，减小E1的绝对值，可使偏航通道晃动呈稳定状态。文献［3］认为，偏航通道晃动不稳定是由模型推导过程中坐标转换顺序不一致引起的，并按坐标转换顺序一致推导了偏航通道晃动方程，但方程中仍含系数E1，似乎晃动稳定性受重力的影响，这使设计人员很难理解。实际工程设计中，为使两个通道的晃动频率特性相同，减小无动力飞行段的攻角，使当地俯仰角控制在3°以内，减小弹道爬升速率，导致火箭运载能力损失。

在某运载火箭飞行试验数据分析过程中，发现无动力飞行段偏航姿态角偏差较大，远超出了设计值，姿态角超差如图1所示。为便于表述，称包含原晃动方程的姿态动力学模型为原模型。由图1可知：原模型仿真所得姿态角偏差远小于飞行实测值，这说明，原模型无法解释此现象，基于原模型设计的控制系统存在不足。

图1 飞行试验结果与原模型仿真姿态角偏差Fig.1 Attitude bias between flight test and old model simulation

综上可知，晃动方程只适应姿态角偏差和攻角、侧滑角为小角度的情况，适应性不佳；可能使人产生误解，认为晃动受重力影响；解释不清试验中出现的姿态角超差现象。采用原模型设计控制系统会损失火箭运载能力，这对某些运载能力紧张的火箭来说是致命的。因此，有必要对晃动特性进行研究，建立适应性更好的晃动方程，以解决晃动不稳定和姿态角超差问题，甚至使控制系统设计不损失火箭运载能力。

2 新晃动方程

由于国内常用等效弹簧－质量模型研究液体晃动，所以本文采用等效弹簧－质量模型描述火箭贮箱内液体晃动，推进剂晃动等效弹簧－质量模型如图2所示。

图2 推进剂晃动等效弹簧－质量模型Fig.2 Equal mass－spring model of propellant sloshing

如图3所示，箭体质心O1在发射惯性坐标系O－XYZ中的矢径为r0，火箭上任意点P相对箭体质心的矢径为ρR，液体晃动质量中心相对箭体产生的位移为ρ，则任意点P在发射惯性系中的矢径可表示为

对式（3）求两阶导数，并考虑ρR为常量，可得任意点P的绝对加速度。有

图3 箭体上任意点位移Fig.3 A point displacement of body

式中：ω1为箭体相对发射惯性系的旋转角速度。假设ω1，ρ为小量，则式（4）可简化为

当用等效弹簧－质量模型描述推进剂晃动时，晃动质量为mpj推进剂受重力、弹簧张力和阻尼力作用。根据牛顿第二定律可得

式中：g为重力加速度矢量；Kpj为弹簧张力系数；Dpj为阻尼力系数。

将式（5）代入式（6），并令 （Ωpj）2＝Kpj／mpj，2ξpjΩpj＝Dpj／mpj，移项处理，可得

式（7）中右边第一项是箭体质心视加速度，第二项为由于箭体旋转引起的绕质心加速度，由此可知推进剂晃动与重力加速度无关。由式（7）可导出推进剂相对箭体横向晃动的标量形式方程为

式中：Eφ＝Tφ／m；Eφ＝Tψ／m；Ekl＝mkl／m；Tφ，Tψ分别为姿控发动机的法向控制力和侧向控制力；Kφ，Kψ取值可为－1，0，1，由姿控发动机工作状况确定；m为火箭质量；下标k，l分别与下标p，j相同，只是为了方程推导表述方便。

将式（10）、（11）分别代入式（8）、（9），可得

式（12）、（13）形式类似，只是式（13）方程右端对应项全部反号。可令zpj＝－Zpj，则式（13）变为

这样，两个晃动方程的形式完全相同，使俯仰和偏航通道的姿态动力学模型的形式完全一致，便于系统设计。

对晃动方程进行小偏量线性化，可得

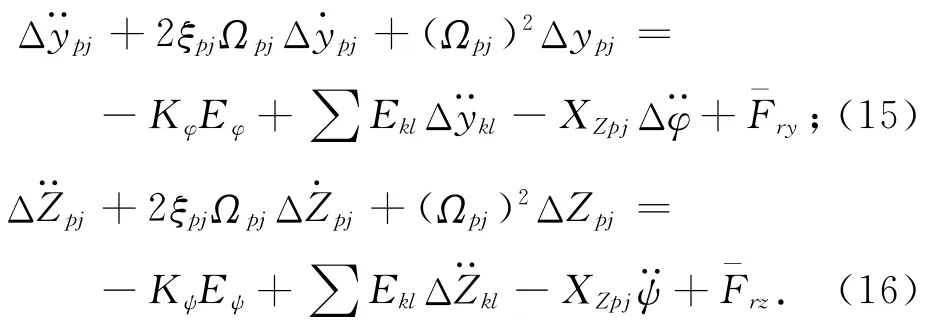
新晃动方程式（15）、（16）与重力加速度无关，且不包含攻角、侧滑角、俯仰角和偏航角等姿态角，可不受这些角度大小的限制，不会损失火箭运载能力，适应性强。

3 仿真分析与试验

为便于表述，称包含新晃动方程的姿态动力学模型为新模型。采用新模型进行控制系统设计分析时，偏航通道晃动与俯仰通道晃动相似，均是稳定的，表明用新晃方程描述晃动特性是合理的，可解决系统设计中偏航通道晃动不稳定现象。

以出现姿态角超差的某运载火箭为对象，选取基于原模型设计的姿态控制律和校正网络参数，采用新模型进行仿真，偏航姿态角偏差仿真结果如图4所示。由图4可知：仿真结果与飞行试验结果很接近。这表明，选取原模型设计的系统参数，采用新模型仿真能复现此运载火箭姿态超差现象。新模型可更准确地描述火箭无动力飞行段的姿态特性。

采用新模型进行后续火箭控制系统设计仿真，并经过多发火箭飞行试验，均未再出现姿态角超差现象。某发火箭采用新模型设计仿真与飞行试验的姿态角偏差如图5所示。由图5可知：新模型设计值与飞行试验结果较吻合，表明新晃动方程合理、正确。

图4 飞行试验结果与新模型仿真姿态角偏差Fig.4 Attitude bias of flight test and new model simulation with old designing parameters

4 结束语

图5 新模型设计的某火箭仿真和飞行试验姿态角偏差Fig.5 Attitude bias of new model designing launch vehicle simulation and flight test

本文采用等效弹簧－质量模型，基于牛顿－欧拉建立了新的晃动方程，表明晃动与重力无关，俯仰和偏航通道的方程形式完全相同，便于控制系统设计。采用新晃动方程，对某液体运载火箭三级无动力飞行段晃动不稳定和姿态角超差现象进行了分析。结果表明：原晃动方程仅适于姿态角偏差和攻角、侧滑角为小角度的情况，会损失火箭运载能力；新晃动方程的适用性更广，可解决晃动不稳定和姿态角超差现象。经实际火箭飞行试验考核，验证了新晃动方程正确可行。

［1］ KIM D H，CHOI J W.Attitude controller design for a launch vehicle with fuel－slosh［C］／／ AIAA Guidance，Navigation，and Control Conference and Exhibit.Denver：AIAA，2000：3851，235－240.

［2］ 孙 平，刘 昆.运载器末助推段非线性姿态控制器设计［J］.上海航天，2011，28（4）：7－11.

［3］ 陈存芸.运载火箭三级无动力飞行段晃动稳定性研究［J］.上海航天，2004，21（4）：29－33.

［4］ 杨云飞，李家文，陈 宇，等.大型捆绑火箭姿态动力学模型研究［J］.中国科学 E辑，2009，39（3）：490－499.

［5］ 徐延万.导弹与航天丛书（控制系统）［M］.北京：宇航出版社，1990.