考虑输入饱和与执行器安装偏差的航天器姿态跟踪控制

宋 斌，颜根廷，郑鹏飞

（上海宇航系统工程研究所，上海 201109）

0 引言

实际航天器姿态控制中，经常面临多种约束的工程设计问题。航天器执行机构不可能输出无限大的力或力矩，这就要求设计的控制律要尽可能满足航天器执行机构最大输出的限制，即输入饱和问题［1－8］。文献［1］提出了一种基于修正的符号函数形式的控制器，通过引入一时变参数证明了系统在输入饱和条件下的严格稳定性。文献［2］提出了一种基于双曲正切函数形式的控制器，通过引入一时变的锐度参数增强了系统对干扰的抑制能力。但上述控制器均是在假设执行机构能精确输出的前提下设计的，实际执行机构的安装总不可避免地存在安装偏差，且该偏差往往对控制精度有较大的影响［9－11］。文献［9］针对执行器不同形式的安装偏差给出了不同的自适应控制方法，但未同时考虑输入饱和受限的问题。

基于上述研究，针对存在参数不确定性、外部干扰、反作用飞轮安装偏差及控制输入饱和受限等多种约束的航天器姿态跟踪问题，本文研究了一种新型的姿态控制方法。

1 问题描述

1.1 航天器姿态跟踪模型

考虑一类刚体航天器，其姿态运动学和动力学方程为

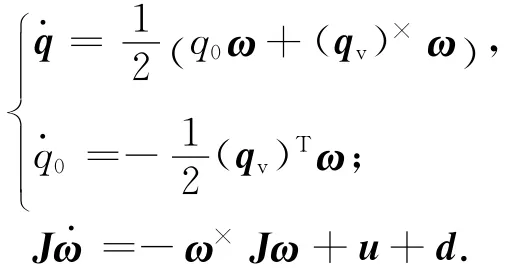
式中：ω＝［ω1ω2ω3］T为航天器的本体系B相对惯性系I的姿态角速度，且表示在航天器的B系中；q＝［q0q1q2q3］T为航天器B系相对I系的姿态四元数；J为航天器的转动惯量矩阵；u＝［u1u2u3］T为实际的控制力矩，且由反作用飞轮提供；d＝［d1d2d3］T为航天器受到的干扰力矩。对任意一向量a＝［a1a2a3］T，定义

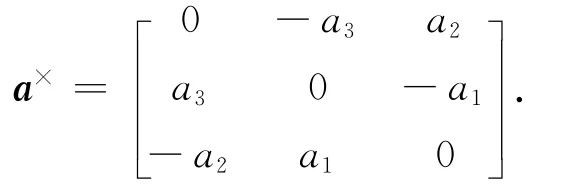
在航天器姿态跟踪过程中，航天器的目标姿态角速度ωd＝［ωd1ωd2ωd3］T为坐标系D相对Ⅰ系的姿态角速度，且表示在坐标系D中；目标姿态四元数qd＝［qd0qd1qd2qd3］T为航天器D系相对Ⅰ系的姿态四元数。

航天器姿态跟踪的模型为

式中：ωe＝［ωe1ωe2ωe3］T为航天器B系相对D系的姿态角速度，且表示在 B系中；qe＝［qe0qe1qe2qe3］T为B系相对D系的姿态四元数，且

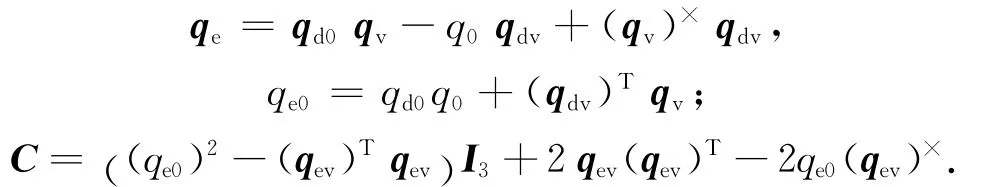
1.2 反作用飞轮安装偏差模型

本文的控制力矩由3个在航天器本体系正交安装的反作用飞轮提供。理想状况下，反作用飞轮构型如图1所示；存在安装偏差状况下，反作用飞轮的构型如图2所示。对图2状况，反作用飞轮的安装偏差矩阵可表示为

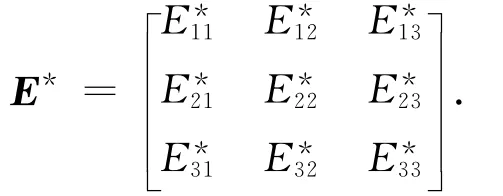
图1 理想状况下反作用飞轮构型Fig.1 Configuration of reaction wheels

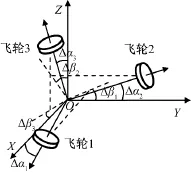
图2 存在安装偏差时反作用飞轮构型Fig.2 Configuration with misalignments

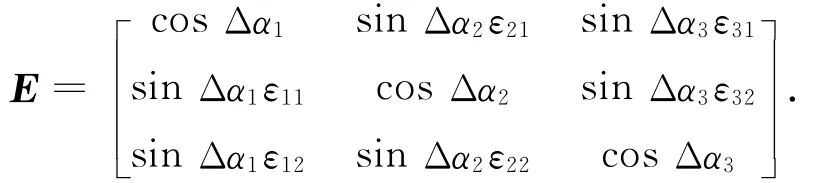
式 中：（εi1）2＋ （εi2）2＝1；εi1，εi2∈ ｛±sin Δβi，±cosΔβi｝。此处：i＝1，2，3。

实际工程中，Δαi≤l是可得到保证的，且l通常是一已知的较小的正的常数（如l＝1°）。因此，E是一个正定的主对角线占优的矩阵。为保证算法的普适性，本文对l值未知时的情况进行了研究，但存在以下合理假设。

假设1：

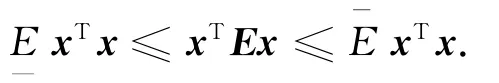
1.3 控制问题描述

定义指令力矩uc＝［uc1uc2uc3］T，若只考虑输入饱和，指令力矩与实际输入力矩关系可表示为

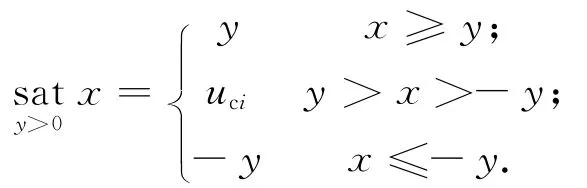
在此基础上，考虑反作用飞轮安装偏差的影响，实际的控制输入可表示为

考虑约束式（4）及外部干扰，针对航天器系统式（1）、（2），设计控制器使系统实现控制目标

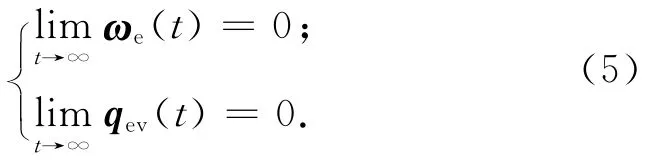
2 控制律设计

定义辅助变量s＝［s1s2s3］T为

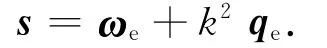
式中：k为一时变参数。

2.1 只考虑输入饱和

有

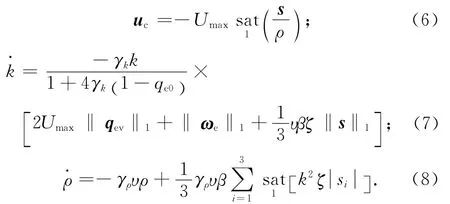
式中：β，ζ，γρ，γk为大于零的常数；υ＝1.5Umax；ρ为控制器调节参数，对扰动和执行器安装偏差自适应补偿；i＝1，2，3。

假设2：

定理1：考虑假设2和约束式（3），系统式（1）、（2）在控制律式（6）和参数自适应律式（7）、（8）作用下，可实现控制目标式（5）。

证明：选择李雅普诺夫函数

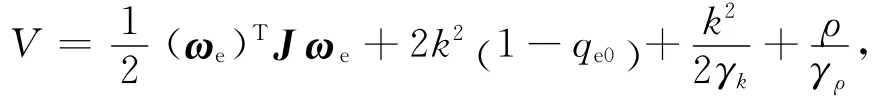
求其时间导数

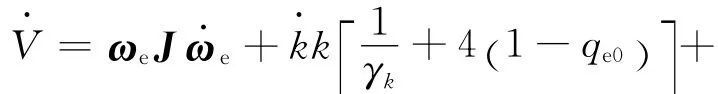
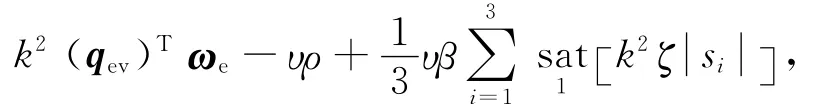
则有

式中：

代入参数自适应更新律式（7），可得

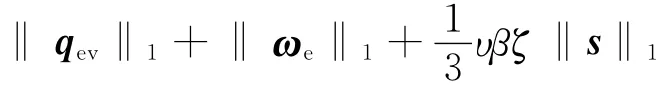
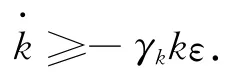
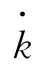
由式（7）还可得

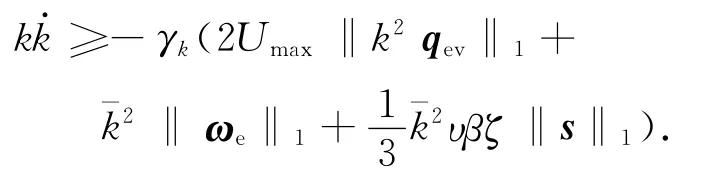
积分后有

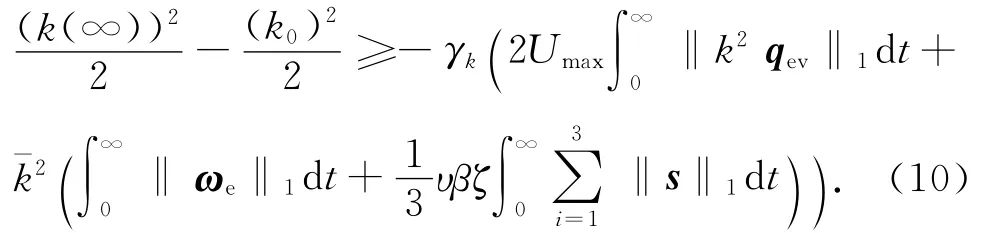
由式（9）可知：式（10）的三个积分项之和有界。设其上界为λ，式（10）可变为

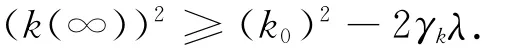
2.2 同时考虑输入饱和与反作用飞轮安装偏差

有

式中：ζ，γυ为大于零的常数；υ为一未知的大于零的常数，且υ＝1.5EUmax；为其估值；为的初始条件。

假设3：

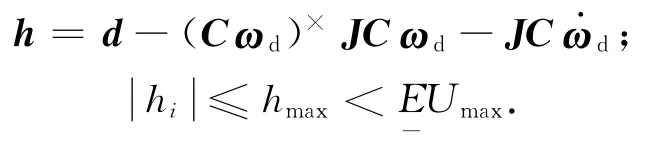
定理2：考虑假设3和约束式（4），系统式（1）、（2）在控制律式（11）和参数自适应律式（12）～（14）作用下，可实现控制目标式（5）。

证明：选择李雅普诺夫函数

求其时间导数

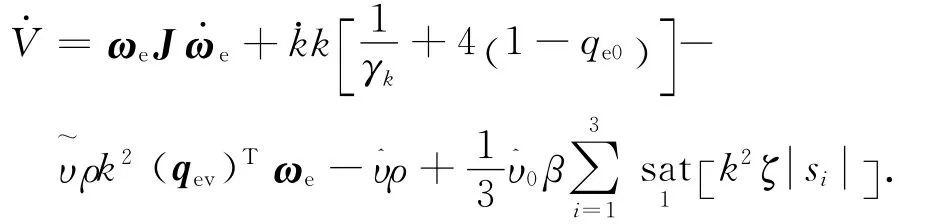
同理有

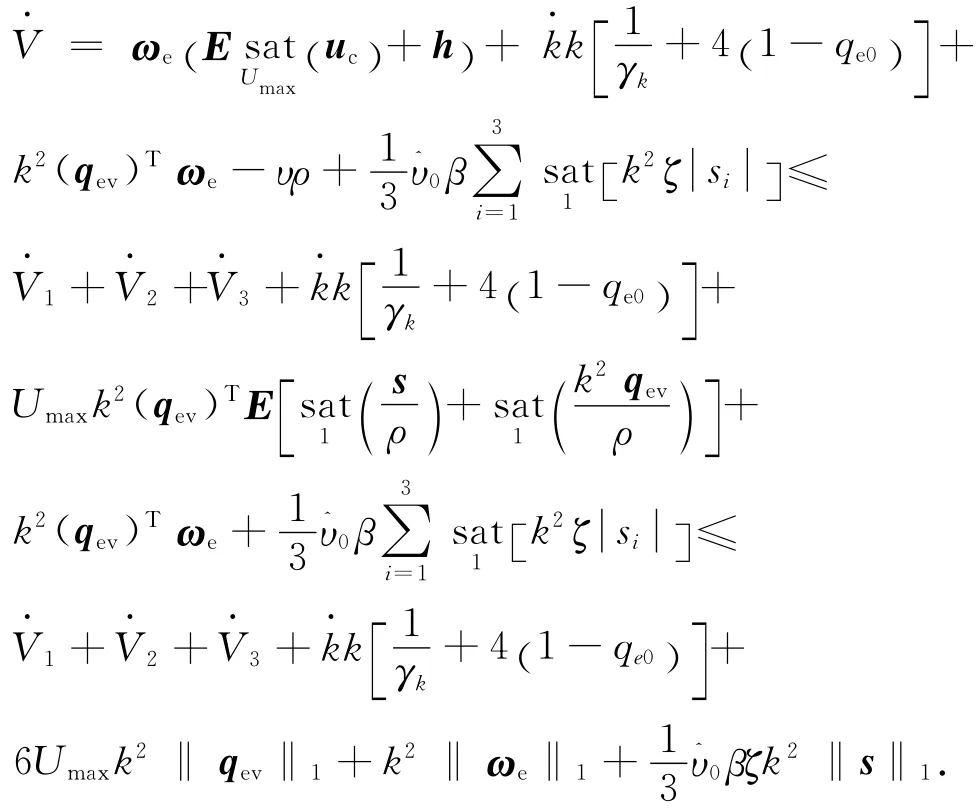
式中：

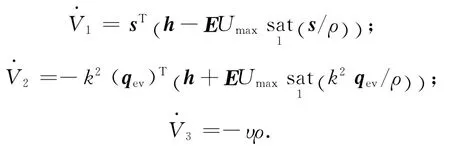
代入参数自适应更新律式（11），可得

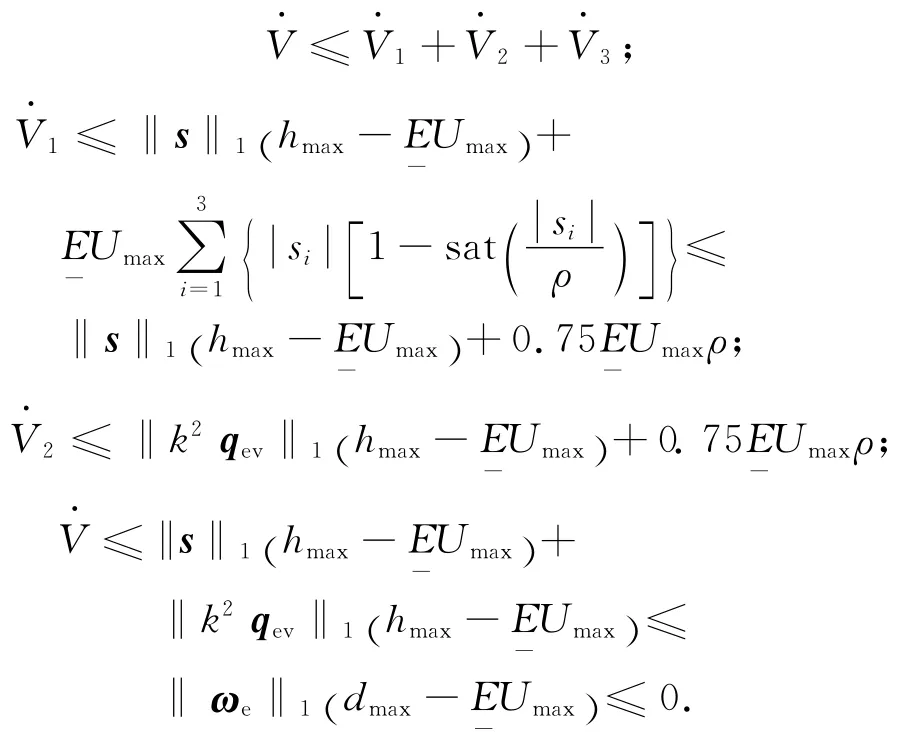
则同样可证明定理2成立。

说明1：为避免有可能发生的抖振，将参数自适应律式（13）修正为

参数自适应律式（8）、（13）可保证0＜ρ≤β（当0＜ρ0≤β）；修正后的参数自适应律可保证γd＜ρ≤β（当γd＜ρ0≤β）；虽然系统由渐近稳定变为有界稳定，但稳态精度仍可满足工程实际的要求。

3 仿真与分析

取航天器参数：J＝diag［20 17 15］kg·m2；Umax＝±0.2N·m；

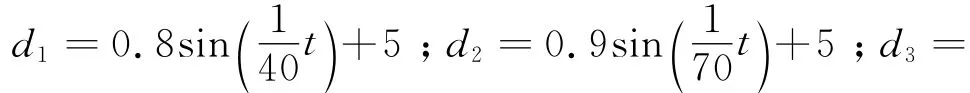
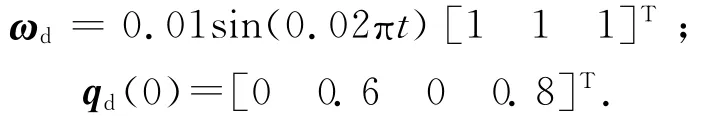
反作用飞轮

a）仿真1结果如图3～9所示。

图3 仿真1姿态响应Fig.3 Time responses of attitude in case 1

由图3～9可知：本文设计的控制方法可满足输入饱和受限的约束，在执行器存在安装偏差及面对外部干扰时，系统的收敛速度和指向精度依然很理想。

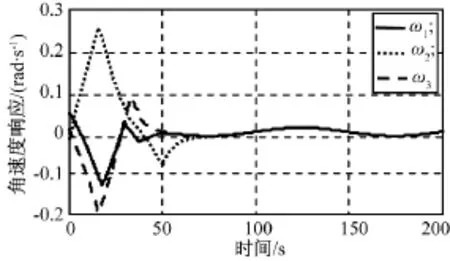
图4 仿真1角速度响应Fig.4 Time responses of velocity in case 1

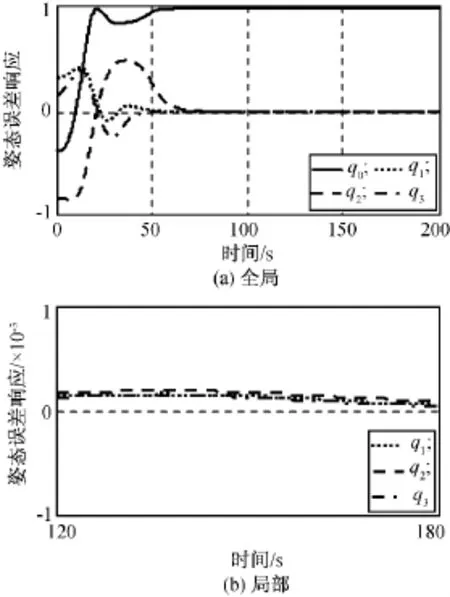
图5 仿真1姿态误差响应Fig.5 Time responses of attitude error in case 1

b）仿真2结果如图10、11所示。

由图10、11可知：在PD控制器作用下，控制精度明显低于本文控制方法，且PD控制器在理论上并不满足输入饱和受限的约束。

4 结束语

本文设计了一种基于饱和函数形式的控制器，引入一时变的参数，理论上证明了系统在输入饱和与执行器安装偏差时的稳定性。另引入一时变锐度参数，增强了系统对干扰的抑制能力和系统对执行器安装偏差的适应能力。控制器中不包含航天器惯量信息，控制器对系统参数的不确定性具有鲁棒性。仿真结果表明：该控制方法可行且有效。

图6 仿真1角速度误差响应Fig.6 Time responses of velocity error in case 1

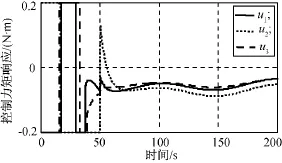
图7 仿真1力矩响应Fig.7 Time responses of torque in case 1

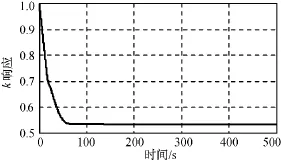
图8 仿真1 k响应Fig.8 Time responses of kin case 1

图9 仿真1ρ响应Fig.9 Time responses ofρin case 1

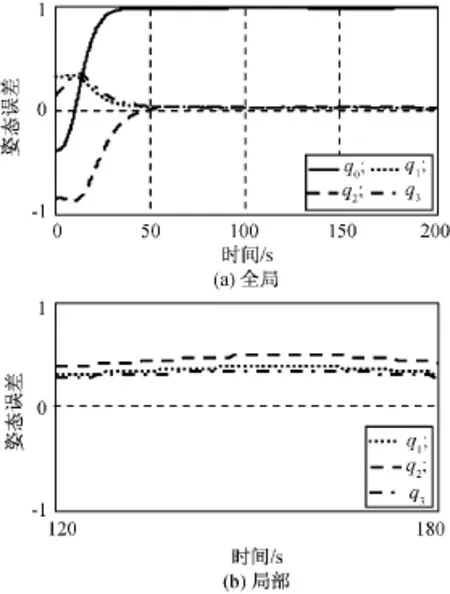
图10 仿真2姿态误差响应Fig.10 Time responses of attitude error in case 2

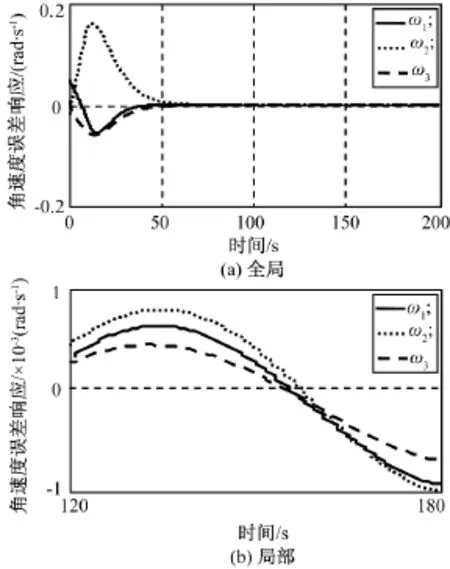
图11 仿真2角速度误差响应Fig.11 Time responses of velocity error in case 2

［1］ BOSKOVIC J D，LI S M，MEHRA R K.Robust tracking control design for spacecraft under control input saturation［J］.Journal of Guidance，Control，and Dynamics，2004，27（4）：627－633.

［2］ WALLSGROVE R J，AKELLA M R.Globally stabilizing saturated attitude control in the presence of bounded unknown disturbances［J］.Journal of Guidance，Control，and Dynamics，2005，28（5）：957－963.

［3］ WIE B，BAILEY D，HEIBERG C.Rapid multitarget acquisition and pointing control of agile spacecraft［J］.Journal of Guidance，Control，and Dynamics，2002，25（1）：96－104.

［4］ HU Q，XIAO B，FRISWELL M I.Robust fault－tolerant control for spacecraft attitude stabilisation subject to input saturation［J］.Control Theory ＆ Applications，IET，2011，5（2）：271－282.

［5］ DIXON W E，De QUEIROZ M S，ZHANG F.Tracking control of robot manipulators with bounded torque inputs［J］.Robotica，1999，17（2）：121－129.

［6］ CAI W，LIAO X，SONG D Y.Indirect robust adaptive fault－tolerant control for attitude tracking of spacecraft［J］.Journal of Guidance，Control，and Dynamics，2008，31（5）：1456－1463.

［7］ ALI I，RADICE G，KIM J.Backstepping control design with actuator torque bound for spacecraft attitude maneuver［J］.Journal of Guidance，Control，and Dynamics，2010，33（1）：254－259.

［8］ 崔祜涛，程小军.考虑有界干扰和输入饱和的航天器姿态抗退绕机动控制［J］.中国科学：技术科学，2012，42（9）：1004－1015.

［9］ MERCKER T H，AKELLA M R.Adaptive estimation and control algorithms for certain independent control axis misalignments［J］.Journal of Guidance，Control，and Dynamics，2014，37（1）：72－85.

［10］ 胡庆雷，李 波，张爱华，等.考虑推力器安装偏差的航天器姿态机动有限时间控制［J］.控制理论与应用，2013，30（4）：417－424.

［11］ 吕跃勇，胡庆雷，马广富，等.考虑执行机构误差的编队卫星姿态分布式时延滑模自适应协同控制［J］.航空学报，2011，32（9）：1686－1695.