多约束航天器飞越式接近的两级运动规划方法
郝 瑞,孟云鹤,郭胜鹏
(国防科学技术大学 航天科学与工程学院,湖南 长沙 410073)
0 引言
在轨服务航天器对大型空间站或卫星进行维护时,首先需实现安全接近过程。飞越式接近方法可使服务航天器沿一条无碰撞的路径到达目标,且保证出现故障时也能安全撤离。文献[1-2]给出了飞越式接近方法的基本过程,并验证了飞越式接近相对基于数值优化方法的接近路径有更好的安全性,且节省燃料。在轨服务航天器飞越式接近目标要求其轨道与姿态同步快速精确机动,属于高维非线性问题,尤其是考虑航天器机动性能及空间环境约束时,一般规划方法难以获得满足要求的轨迹。
快速搜索随机树(RRT)算法广泛用于运动规划问题[3]。有研究发现基本RRT算法结果为概率非最优,并通过在生成新节点时加入最优路径选择,得到RRT*算法。文献[4]对RRT*算法进一步改进,通过限定最大存储节点数,得到了搜索效率更高的RRT*FN算法。Heuristically-guided RRT(hRRT)算法引入了类似的近邻节点概念[5]。文献[6]在其基础上采用多重随机采样策略,得到了满足无人机实时航迹规划需求的改进RRT算法。文献[7]针对RRT规划方法易进入局部陷阱的缺点,在算法中引入考虑障碍约束的平衡生长机制,提高了算法的绕障碍能力,使其在解决高维、复杂约束规划问题时有较高的可靠性。文献[8]提出了两级路径规划方法,先用RRT算法规划路径初值,再将路径优化转化为最优控制问题,用高斯伪谱法(GPM)求解。RRT-GPM方法的缺点是使用SNOPT非线性求解器求解非线性系统时常出现收敛困难。
本文基于复合轨迹规划,对一种由RRT运动规划算法与进化算法(EA)结合的两级轨迹规划方法进行了研究。
1 问题描述
1.1 飞越式接近过程
根据文献[1],飞越式接近过程分为末端接近段、轨迹修正段和飞越接近段(如图1所示),如接近中发生意外,服务航天器将会进入飞越逃离段。假定末端接近段完成了轨迹修正过程,则需研究飞越接近段的起点运动状态确定与末端接近段的轨迹规划问题。

图1 飞越接近Fig.1 Fly-by approach
已知初始相对运动状态与飞越式接近总任务时间,则接近轨迹确定步骤如下:
a)由目标卫星运动状态的测量值算得飞越接近目标点的运动状态;
b)选择合适的飞越近阶段时间,计算飞越接近段初始点,确保其处于安全区域;
c)已知末端接近段的初始运动状态、目标运动状态与调整时间,对该段的运动轨迹进行规划。
本文用Hill坐标系描述相对轨道运动,且假设轨道为圆轨道。以服务航天器出发时刻为零时刻,飞越接近总任务时间为T,末端接近段时间为t,则飞越接近段时间为T-t。服务航天器预测得到目标相对轨道运动状态为[(rT)H(vT)H]T,且要求其姿态为(qT)H,角速度(ωT)H=0,则求解得到时刻t相对轨道运动状态。此处:(rt)H,(vt)H分别为飞越式接近初始点的相对位置与速度;Φ11,Φ12,Φ21,Φ22为轨道运动转移阵。

1.2 末端接近段的轨迹规划问题
1.2.1 运动状态与状态空间
已知末端接近段的初始和目标运动状态分别为

式中:(ω0)H,(ωt)H分别为初始时刻和时刻t的角速度。轨迹规划问题中的运动状态还应包含时间状态t,则服务航天器的运动状态描述

由于服务航天器的最优运动轨迹可能在障碍区域附近,规划问题的总状态空间应包括自由运动集合Xfree及障碍Xobs,即状态空间X=Xfree∪Xobs。
1.2.2 运动状态度量
运动状态的度量主要用于描述运动状态空间中的距离。本文用实数方程ρ(pi,pj)表述服务航天器两个运动状态间的度量,有

式中:K1~K5为权系数;ρ(qi,qj)为姿态四元数间的度量,且

式(4)表示两个姿态间度量是四元数qi与qj,-qj两个距离中的最小值,这是因为qj,-qj代表同一姿态的两种旋转方式[8]。此处:‖qi-qj‖=arccos(qi·qj)。
1.2.3 约束条件
末端接近段路径规划问题主要考虑运动动力学约束和空间几何约束[9-10]。
a)运动动力学约束
推进装置提供的轨道运动所需的加速度和速、执行机构提供的最大姿态控制力矩,以及有效载荷对运动速度的限制等,分别对速度、加速度、姿态角速度和角加速度提出了约束要求[11]。可表示为

b)空间几何约束
空间几何约束主要指空间环境中固定或时变的实体障碍约束或航天器指向约束等。假设所有约束均为实体障碍约束,即

式中:Robs为障碍影响半径;Rmin为航天器最小安全半径;edge(ri,ri+1)为两相邻状态间的路径。式(6)的第一式表示航天器本体不与实体障碍相交;第二式表示edge(ri,ri+1)可保证航天器整体在运动过程中不与障碍区相交。
2 末端接近段的两级运动规划方法
用改进的双向平衡RRT规划算法与进化算法结合的两级运动规划方法对在轨服务航天器的末端接近段进行分析,并对该规划方法的基本内容进行描述。其中两级轨迹规划方法的主要流程如图2所示。

图2 两级轨迹规划算法流程Fig.2 Flowchart for two-stage path planning method
2.1 基于改进双向平衡RRT算法的初始轨迹规划
2.1.1 局部规划器
局部规划器主要用于确定节点pi,pj间的运动,要求其满足整体算法的快速性需求[12]。已知两节点状态pi,pj,认为从pi出发至pj的平动速度方向与姿态运动角速度矢量方向保持不变。此处规划器的作用是求取从pi出发经过时间Δt的新节点pi+1,要求两节点的时间状态应满足tj-tj≥Δt,以保证时间不可逆的要求。新节点pi+1可表示为


e1,e2分别为从节点pi到pi+1的速度和旋转角速度方向单位矢量。
2.1.2 改进的双向平衡RRT算法
图2给出了改进的双向平衡RRT的主要规划步骤,通过比较TreeA,TreeB两搜索树的节点数实现互换,实现两树的平衡生长。在此基础上,当某方向随机树所求新节点的预测点不满足障碍约束时,则程序换为先计算该随机树。这种改进可解决由障碍相对较大带来的近距障碍“陷阱”问题(如图3所示)。两搜索树在同一次搜索中分别按规划方法求出新节点a和预测点b。由于障碍较大,预测点b不满足障碍约束,又因为新节点a在更换随机点后仍在障碍附近,从而使TreeB得不到合适的预测点,导致迭代受阻。改进后,若预测点b不满足障碍约束条件,则重新生成随机点,并先计算出新节点c。
2.2 基于进化算法的光滑轨迹规划方法

图3 障碍相对较大时运动规划Fig.3 Motion planning when obstacles were relatively large
因RRT规划算法中节点随机生长,有限次数搜索得到的结果一般是曲折轨迹,故可用基于进化算法的光滑轨迹规划方法对初始轨迹进行优化。由于进化算法简单、实现易且使用效果明显,在最优化、机器学习和并行处理等领域得到了广泛应用[13]。
光滑轨迹规划的目标是找到使轨迹接近最优轨迹的一组函数系数(如图2所示)。将服务航天器的全部约束作为算法的约束条件,以曲线上对应时间点的取值与样本点状态的偏差作为优化指标,当偏差小于预定目标时输出当前最优的一组系数。最后将系数代入拟合函数得到优化的光滑运动轨迹。选用的状态拟合函数为带有权系数的拉格朗日插值多项式

式中:Xi为待拟合参数在第i个样本点处的取值;n为样本点数;ki为第i状态点的权系数,即为待优化曲线参数;ti为第i状态点对应的时间。X(t)的一阶导数形式为

为比较RRT算法结果与拟合得到的优化结果,设计了轨迹的代价值

式中:n为RRT算法所得轨迹中总的节点数;δpi,δvi,δqi,δωi,δti分别为第i节点相对上一节点的位置、速度、四元数、角速度和时间的变化量;k1~k5为系数,作用是将各状态量调整到统一或近似量级。
3 算例
3.1 末端接近段运动规划的相关参数
为简便直观,将运动规划坐标系(Y、Z轴与质心轨道坐标系方向相反)原点设在末端接近段的初始位置,且规划过程中只考虑速度、角速度的大小,则在此坐标系中规划问题基本参数为:初始位置[0 0 0]Tm;目标位置[42.22 38.44 41.45]Tm;速度,初值0m/s,目标值0.142m/s;初始姿态

目标姿态

角速度,初值和目标值均为0rad/s;目标时间100s;飞行区域[43 43 43]m;障碍参数,球心[10.5 10.5 7.5]Tm,[31.5 31.5 34.5]Tm,立方体中心
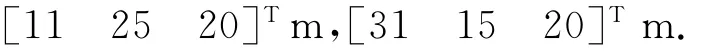
3.2 末端接近段初始运动规划
设服务航天器运动动力学约束条件为恒定值,速度、加速度、角速度与角加速度的最大值分别为2.5m/s,0.4m/s2,0.2rad/s,0.05rad/s2。以一次仿真结果为例,步长2s时100 000次所用搜索时间241.5s,找到325路径,其中代价最小值为53.90。最优结果如图4所示。
增加搜索次数可降低轨迹所需的代价值,但根据文献[3],搜索次数较大时,增加计算量对代价值降低的效果并不明显,很难找到更优路径。
3.3 基于进化算法的光滑轨迹规划
取100 000次搜索所得结果中的20个状态点作为初始点,进化算法参数设置为种群数200个;新个体30个;进化代数800;适应度函数0.25。其中一次时间为452.6s,拟合所得轨迹和四元数如图5所示。
拟合前后的速度、角速度、加速度和角加速度如图6所示。由图可知:拟合获得了运动状态的光滑连续曲线,且满足服务航天器运动动力学与空间障碍约束;代价值为41.79,降低了22.5%,实现了初始轨迹的优化;拟合曲线初始状态、目标状态与末端接近段要求的误差很小。

图4 100 000次搜索结果Fig.4 Result for search of 100 000times

图5 轨迹与姿态拟合结果Fig.5 Fitting results of orbit and attitude
RRT,EA算法的速度、角速度、加速度和角加速度功率谱如图7所示。由图可知:基于进化策略的平滑充分过滤了RRT轨迹规划结果中的高频项,使航天器的运动过程更平稳,这是该法更节省燃耗、代价指标更低的原因,平滑后的结果更利于工程实现。

图6 各状态量拟合前后对比Fig.6 Comparison of all states before and after fitting

图7 功率谱分析Fig.7 Power spectrum analysis
3 结束语
本文利用基于采样理论的快速搜索随机树方法解决高维问题的快速性以及进化算法处理优化问题的强鲁棒性特点,提出了一种两级轨迹规划方法。先用改进的双向平衡搜索方式的RRT规划方法,快速得到初始运动轨迹,再用进化算法将轨迹拟合为光滑连续曲线,使代价指标进一步优化。仿真结果表明:在满足飞越式接近要求的同时,实现了对快速搜索随机树所得初始轨迹的优化,降低了代价值,同时克服了进化算法解决此类复杂约束问题时效率低的缺陷,确保了规划速度,将总规划时间控制在可接受范围内。
[1] MATSUMOTO S,DUBOWSKY S,JACOBSEN S,et al.Fly-by approach and guidance for uncontrolled rotating satellite capture:AIAA Guidance,Navigation,and Control Conference and Exhibit[C].Austin:2003.
[2] MATSUMOTO S,JACOBSEN S,DUBOWSKY S,et al.Approach planning and guidance for uncontrolled rotating satellite capture considering collision avoidance:Proceeding of the 7th International Symposium on Artificial Intelligence,Robotics and Automation in Space:i-SAIRAS 2003[C].NARA:2003.
[3] LAVALLE S M,KUFFNER J J.Randomized kinodynamic planning[J].International Journal of Robotics Research,2001,20:378-400.
[4] ADIYATOV O,VAROL H A.Rapidly-exploring random tree based memory efficient motion planning[C]//Mechatronics and Automation (ICMA),2013 IEEE International Conference on,2013.[s.l.]:[s.n.],2013:354-359.
[5] URMSON C,SIMMONS R.Approaches for heuristically biasing RRT growth[C].Proceedings of the IEEE Conference on Intelligent Robots and Systems.Las Vegas:IEEE,2003:1178-1183.
[6] 彭 辉,王 林,沈林成.区域目标搜索中基于改进RRT的UAV实时航迹规划[J].国防科技大学学报,2009,31(5):86-91.
[7] 王 平,郭继峰,史小宁,等.基于时间状态的敏捷自主在轨服务航天器协同运动规划方法研究[J].控制与决策,2011,26(11):1699-1705.
[8] AOUDE G S,HOW J P,GARCIA I M.Two-stage path planning approach for designing multiple spacecraft reconfiguration maneuvers[J].Journal of the Astronautical Sciences,2008,56(4):515-544.
[9] HUNTINGTON G T.Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D].Cambridge:Massachusetts Institute of Technology,2007.
[10] 仲维国,崔平远,崔枯涛.航天器复杂约束姿态机动的自主规划[J].航空学报,2007,28(5):1091-1097.
[11] GARCIA I M,HOW J P.Trajectory optimization for satellite reconfiguration maneuvers with position and attitude constraints[C]// American Control Conf.Portland:[s.n.],2005:889-894.
[12] CREAMER G,DELAHUNT P,GATES S,et al.Attitude determination and control of cementine during Lunar mapping description and on-orbit performance[C].AIAA Guidance,Navigation,and Control Conf.Baltimore:[s.n.],1995:920-930.
[13] KAVRAKI L E,LAVALLE S M,SICILIANO I B,et al.Springer handbook of robotics[M].Berlin:Springer-Verlag,2008:109-133.
[14] TASGETIREN M F,SUGANTHAN P N,PAN Q K,et al.An ensemble of differential evolution algorithms for constrained function optimization:Evolution Computation (CEC),2010IEEE Congress on[C].IEEE,2010:1-8.

