月球轨道目标表面月球红外辐射热流精细计算方法研究

李 鹏，赵吉喆，来霄毅，李志刚

（1.上海宇航系统工程研究所，上海 201108；2.上海卫星工程研究所，上海 200240）

0 引言

目标热流计算中，星体红外辐射热流（角系数）的求解较麻烦。对地球红外辐射热流，关键是计算地球红外角系数，采用了多种计算方法，不断简化计算过程和提高计算精度［1－4］。月球红外辐射热流的计算与地球红外辐射热流不同，因月球表面大气极为稀薄，几乎无大气层和大气活动，表面直接通过热辐射和宇宙空间交换热量，月球表面温度随纬度变化剧烈，月球红外辐射热流需进行月球红外角系数和月表温度的耦合计算。文献［5］效仿地球红外辐射，计算得到月球平均红外热流，将月球红外辐射假设为一恒定的值；文献［6］根据月表温度的分布特点，将月表的红外辐射划分3个阶梯，连续分布的月球红外辐射热流近似为阶梯分布的形式。上述文献的假设和近似，使计算得到的月球红外辐射热流与实际存在较大偏差。本文基于月球表面对月球轨道目标表面红外辐射热流的积分计算公式，结合坐标转换和向量运算，采用离散化处理，提出了月球轨道目标表面月球红外辐射精细计算方法。

1 月面微元选取

为便于计算任意轨道位置目标表面受到的月球红外辐射热流，本文采用均匀模拟法进行月面微元的选取［7］。

建立直角坐标系o′-x′y′z′（如图1所示）：以目标位置矢量为o′x′轴；o′z轴垂直于轨道平面；o′y′轴与o′x′、o′z′轴满足右手正交关系。其中：目标位置矢量可由目标轨道算得。用天顶角θ和方位角φ描述月面微元ds的位置，如图2所示，则目标位置的坐标为（Rcosθ，Rsinθsinφ，Rsinθcosφ），月面微元的φ在0～2π内均匀分布，天顶角的范围由目标可观测到的月面决定，其中，最大天顶角

式中：R为月球半径；H为目标的轨道高度。

将θ，φ在取值范围内分别N1，N2等分，用每个微元中心对应的θ，φ值描述其位置，则月面微元的面积可表示为

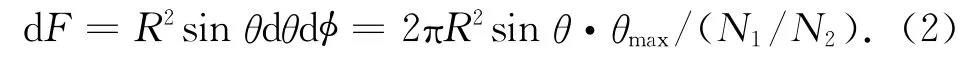
为进行矢量的运算，需要将月面微元位置描述由o′-x′y′z′系转移到月心赤道坐标系O-XYZ中。依次为绕o′z′轴旋转－（υ＋ω），绕o′x′轴旋转－i，绕o′z′轴旋转－Ω，此时月面微元在月心赤道坐标系中的位置矢量

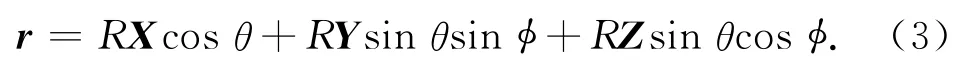
式中：X，Y，Z分 别 为 坐 标 轴o′x′、o′y′、o′z′在OXYZ系的单位向量；υ，ω，Ω，i分别为目标轨道的真近点角、近地点幅角、升交点赤经和轨道倾角。

式中：R为转换矩阵，R＝Rz（－Ω）Rx（－i）Rz（－υω）；

此处：Rx，Ry，Rz分别为绕o′x′、o′y′、o′z′轴旋转的转换矩阵。

2 月球红外辐射热流

月球轨道目标、月球、太阳辐照关系如图3所示，则目标所能观测的月球表面的任意微元ds对目标面元dA的红外辐射热流密度

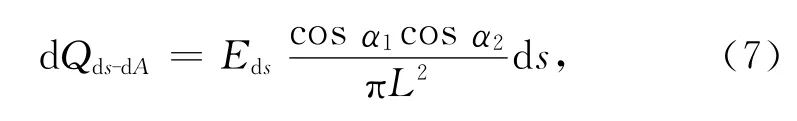
若cosα2＜0，则cosα2＝0。

图3 月球红外辐射计算相关角度Fig.3 Angles for computation of moon infrared radiation

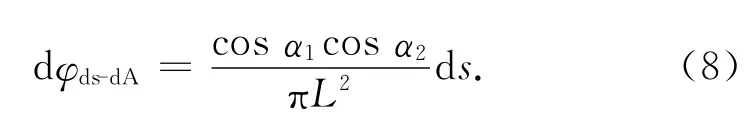
式中：dφds－dA为任意微元ds对目标面元dA的角系数；Eds为月面微元的辐射强度；α1为月表微元和目标面元的连线与月表微元法线的夹角；α2为月表微元和目标面元的连线与目标面元法线的夹角；L为面元至目标的距离。

在O-XYZ系中，目标面元的位置矢量和法线矢量分别为PdA，PndA；太阳的位置矢量为Psun；月面微元位置及其法线的矢量分别为Pds，Pnds，月面微元－目标面元连线位置矢量为Pds－dA，其方向指向目标，则

对目标所能观测的月球表面均匀采样，只要微元数N达到一定数目，通过月面微元对目标面元辐射热流的累积，就能以较高精度的算得月球轨道目标表面的月球红外辐射热流，则

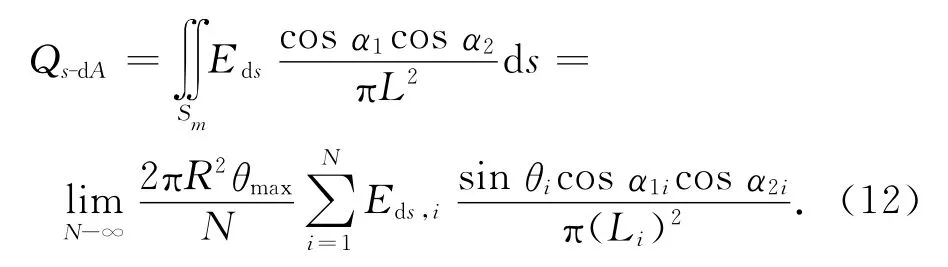
式中：Sm为目标可观测到的月面面积；N＝N1N2。

3 月球表面红外辐射强度

月球地表温度与纬度、地表土壤的热物性有关，目前月壤的物性主要来自有限的样本，不够准确和全面。本文不考虑月球地表热物性的影响，根据能量平衡关系，即月球日照面每一微面积的红外热流和吸收的太阳热流能量平衡，可得月表红外热流计算式为

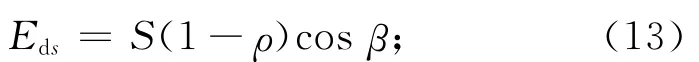
月面微元的温度

式中：S为太阳常数；ρ为月球反射率；β为太阳角，定义为太阳的位置矢量与月面微元法线的矢量的夹角（参见图2）；σ为斯蒂芬－波尔兹曼常数［7］。

由矢量运算公式可得

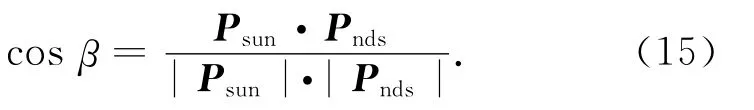
4 目标面元轨道上位置与法线矢量计算

如目标轨道六根数已确定，就可计算出任何时刻目标的位置，其计算式为

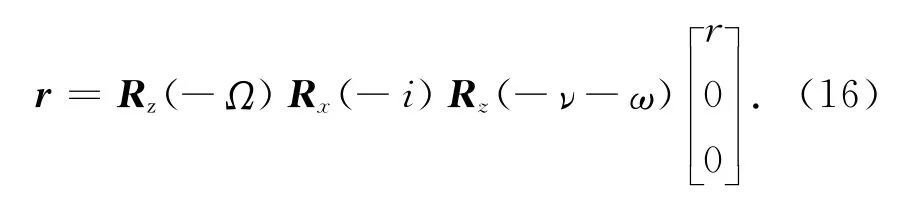
式中：r为目标的位置矢量；r为月心赤道坐标系中坐标原点至目标的距离，且

此处：a，e分别为半长轴和偏心率［8］。

目标面元法线矢量计算式为

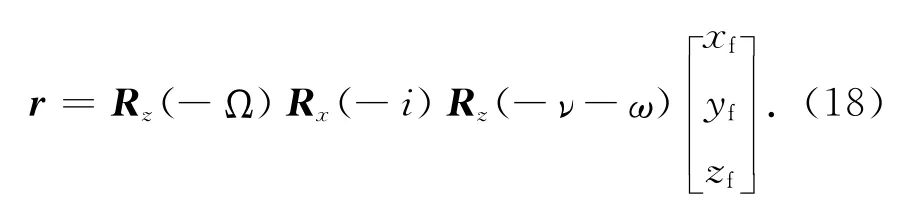
式中：［xfyfzf］T为目标面元法线在o′-x′y′z′系中的单位矢量。

5 计算验证及实例分析

5.1 计算验证

用本文计算方法和计算程序计算典型工况下地球红外辐射角系数，与辐射交换系数手册中理论解析公式得到的相应工况下地球红外辐射角系数进行比对，验证本文计算方法的有效性，结果见表1［9］。对应的工况为：H＝300km，目标表面法线与目标－地心连线的夹角δ变化范围为0°～180°。由表可知：本文的计算结果和辐射交换角系数手册（解析解）的数据非常接近。

5.2 实例计算与分析

选取典型月球轨道：圆轨道，高度200km，轨道参数中轨道倾角i和升交点赤经Ω变化，其他均设为0。太阳沿月心赤道坐标系的－X向入射，S＝1 414W／m2。分别在i＝0°，Ω＝0°；i＝30°，Ω＝30°；i＝60°，Ω＝60°；i＝90°，Ω＝90°条件下计算，所得不同绕轨道飞行角度时目标表面所受月球红外辐射热流密度和对应的月表温度如图4所示，目标表面所受月球红外辐射热流密度如图5所示。各曲线的0°为相应轨道的升交点，同时仿效地球红辐射的特点，将月球红外辐射进行整个月表面积上的平均，计算出月球轨道上目标表面的平均月球红外热流密度。由图可知：月球轨道目标表面所受的月球红外辐射热流在整个轨道周期内，特别是在阳光区变化很大，阳光区月球红外辐射热流最大1 000W／m2，与太阳辐射的热流强度相当，阴影区月球红外辐射热流接近于零；不同月球轨道上目标表面所受月球红外辐射热流周期变化的差异亦很大，与目标表面对应的月面区域的温度的变化相呼应，当太阳光入射矢量与轨道面垂直（如i＝90°，Ω＝90°）时，月球轨道位于月球光照区和阴影区的交界面内，目标表面所受的月球红外辐射热流在轨道周期内为一定值（40W／m2）；仿效地球红辐射的特点，将月球红外辐射进行整个月表面积上的平均，得到目标表面的平均月球红外热流密度253W／m2，月球红外辐射与地球红外辐射的特点有较大差异。在月球轨道飞行器热控设计时，应充分考虑月球红外辐射的特点，对月球红外辐射进行精确的模拟。

图5 不同月球轨道上月球红外辐射热流周期内变化Fig.5 Varietion of moon infrared radian with different orbits

图6 不同δ下周期内月球红外辐射热流Fig.6 Moon infrared radian with different angleδ

不同δ下，轨道周期内（轨道为i＝0°，Ω＝0°）目标表面所受月球红外辐射热流如图6所示。由图可知：随着δ的增大，目标表面所受月球红外辐射热流逐渐减小，当δ大于一定角度后，月球红外辐射热流为0，这是合理的。可见，采用本文的模型和方法可计算任意形状的飞行器任意表面所受月球红外辐射热流。

6 结束语

本文对月球轨道目标表面月球红外辐射的精细计算方法进行了研究。该法用坐标转换和向量运算，便于编程计算，同时有广泛的通用性，可计算得到任意星体、任意轨道、任意几何形状目标的星体红外辐射热流。用本文的方法算得的典型工况下地球红外辐射角系数，与辐射交换系数手册中理论解析公式得到的相应工况下地球红外辐射角系数相近，间接地验证了本文计算方法的有效性和较高的计算精度。

［1］ 翁建华，潘增富，闵桂荣.空间任意凸面的轨道空间外热流计算方法［J］.中国空间科学技术，1994，14（2）：11-18.

［2］ 张 涛，张 冰.计算近地轨道航天器空间外热流的RUD方法［J］.宇航学报，2009，30（1）：338-343.

［3］ 张立新.轨道空间外热流计算的一种新方法［J］.光学精密工程，1995，3（6）：80-85.

［4］ 王雨飞，李 强，廖 胜.目标表面地球辐射和地球反照的均匀模拟法［J］.红外，2011，32（1）：40-44.

［5］ 张加迅，文耀普，李劲东.单自由度太阳帆板极月轨道月球卫星的初步热分析与热设计［J］.空间科学学报，2004，24（1）：51-57.

［6］ 侯欣宾，邵兴国，徐 丽，等.嫦娥一号卫星热设计及计算分析［J］.航天器工程，2006，15（4）：21-26.

［7］ 徐向华，梁新刚，任建勋.月球表面热环境数值分析［J］.宇航学报，2006，27（2）：153-156.

［8］ 张玉祥.人造卫星测轨方法［M］.北京：国防工业出版社，2007.

［9］ 杨贤荣，马庆芳，原庚新，等.辐射换热角系数手册［M］.北京：国防工业出版社，1982.