两平行构型双框架磁悬浮变速控制力矩陀螺操纵律设计
孙宏丽,项 飞,李结冻,曹震宇,谭天乐
(1.上海航天控制技术研究所,上海 200233;2.上海市空间智能控制技术重点实验室,上海 200233)
0 引言
随着航天技术的发展,动量交换装置因其输出范围大、响应快且可连续变化、不消耗工质等优点日益频繁地用于航天器姿态控制系统[1]。DGMSCMG不仅能满足高精度、长寿命要求,而且可降低姿控执行机构的体积和质量,是航天器实现高精度和快速机动姿控的理想执行机构[2]。目前,将磁悬浮SGCMG作为执行机构已有实际应用,如1986年发射的和平号空间站,但对其动力学与控制系统的研究并未见深入报道[3]。
文献[4]获得了应用于航天器的磁悬浮内转子的动力学模型,用仿真分析各部分的耦合影响。对磁悬浮转子系统的稳定性控制,文献[5]分析了转子转速与稳定性的关系。但这些研究都是分析静框架下的转子特性,均未考虑载体运动的影响。文献[6]分析了DGMSCMG的动力学耦合机理,提出了一种基于复合控制的补偿方法对磁悬浮转子稳定性进行控制,但仅限于静基座下DGMSCMG的动框架效应补偿。文献[7]研究了平行构型变速控制力矩陀螺群的控制律及其在航天器姿态控制中的应用。通常控制力矩陀螺在姿态控制中,需解决框架构型奇异的情况,设计的控制律可在一定程度上避免奇异。平行构型CMG避免奇异的性能较好,能在多数情况下顺利地避免奇异,但有些情况避免奇异时会有时间延迟,适于单轴航天器姿态机动情况。
为用VSDGCMG实现航天器姿态控制,须设计良好的操纵律,将姿态控制所需的力矩指令分解为每个VSDGCMG的框架CMG和飞轮RW指令,在操纵律设计中考虑CMG,RW模式的切换[8]。本文研究了两VSDGCMG的操纵律设计及实现。
1 坐标系定义
为便于基于磁悬浮VSDGCMG的航天器动力学建模,定义以下各坐标系,如图1所示。

图1 各坐标系示意Fig.1 Sketch of coordinates
惯性坐标系Oi-xiyizi:用地心赤道坐标系替代惯性坐标系,原点Oi位于地心,Oixi、Oizi轴分别指向春分点和北极,并与Oiyi轴构成右手坐标系。
质心轨道坐标系O-xoyozo:以航天器质心O为原点,滚动轴Oxo沿轨道平面与当地水平面的交线,指向前进方向;偏航轴Ozo轴沿当地垂线指向地心;俯仰轴Oyo轴垂直于轨道平面。O-xoyozo系在空间以卫星的轨道角速度ωo绕Oyo轴旋转,且旋转方向与Oyo轴的方向相反。
星体主轴坐标系(本体系)O-xbybzb:原点O为航天器质心,Oxb、Oyb、Ozb轴固定在卫星本体上,且分别为卫星的三个惯量主轴。设[φθψ]T为航天器相对轨道坐标系的3-1-2Euler角。
零位置坐标系(零系)O-xsyszs:外框架坐标系在零位置时与之重合。零系与本体系固连,Csb为零系至本体系的转换矩阵,与各磁悬浮VSDGCMG在航天器上的安装方位(即CMG的构型)有关,为常值矩阵。
外框坐标系O-xjyjzj:与外框固连,θj为外框架角度,转子绕Oyj轴的转动角度,以ωj为正时转角为正值。
内框坐标系O-xgygzg:与内框固连,θg为内框架相对转动角度,转子绕Oxg轴的转动角度,以ωg为正时转角为正值。
转子坐标系O-xryrzr:与转子固连,相对内环坐标系仅有关于Ozr轴的自转自由度,转子自转角为Ωt。
令Ω为常值角速度矢量,在转子坐标系中表示为[0 0Ω]T;Cba为从坐标系a至坐标系b的正交坐标转换阵;y/m为矢量y在m系中的投影;Jb,Jj,Jg,Jr分别为航天器本体、外框架、内框架、磁悬浮转子的转动惯量阵;x×为任一向量x×=[x1x2x3]T的斜对称阵。
2 操纵律设计
2.1 动力学方程
将两VSDGCMG平行安装在刚体航天器上,如图2所示。图中:gji,ggi,gsi分别为第i个 VSDGCMG的外框架轴向单位矢量、内框架轴向单位矢量和转子轴向单位矢量;gt1=gj1×gs1,gt3=gg3×gs3分别为第1个VSDGCMG外、内框架角速率输出力矩方向上的单位矢量;gt2=gj2×gs2,gt4=gg1×gs1分别为第2个VSDGCMG外框架角速率输出力矩方向上的单位矢量。

图2 两VSDGCMGFig.2 Parallel variable speed double gimbaled control moment gyros
因框架角速率及航天器角速度远小于转子转速,故可忽略其对系统角动量的影响。设第i个VSDGCMG转子的极转动惯量为Jri,角速度为Ωi,则其角动量hi=JriΩigsi。则两VSDGCMG的总角动量

将H对时间求导,即得两平行构型VSDGCMG的输出力矩,合成的陀螺力矩写成矩阵形式MB,则有


2.2 模式切换算法
两VSDGCMG操纵律设计的核心是根据姿态控制所需指令力矩Lr=MB-FΩ,产生框架角速率指令和内转子转子角加速度指令。通过设计模式切换算法可将姿态控制所需Lr分解为CMG指令力矩LCMG和RW指令力矩LRW。
式(2)可分解为


2.3 CMG操纵律
VSDGCMG的框架角分布决定了框架角速率输出力矩方向,故决定其CMG奇异状态。为定量描述VSDGCMG的CMG奇异状态,需定义CMG奇异测度函数。基于两VSDGCMG的CMG奇异测度函数设计零运动,可改变其框架角分布,使其逃离CMG奇异。定义矩阵

则D中各向量的三维空间分布表征了两VSDGCMG的CMG模式三维力矩输出能力,用该矩阵的奇异值可设计出两VSDGCMG的CMG奇异测度函数。
定义CMG奇异测度函数

式中:σ1,σ3分别为D奇异值分解后所得最大和最小奇异值,可表示成ρ的函数。κ值越接近0,表明D越远离奇异,即CMG越远离奇异。
考虑奇异回避及能量消耗,得控制目标函数

式中:W1为正定加权阵;Δt为达到框架角指令的时间。
为获得式(7)的最小范数解,可在目标函数中引入Lagrange乘子向量λ1,

则L1)的极小值条件为

可得

式中:g为CMG输出力矩方向。将式(14)代入式(7)可得

将式(15)代入式(14)得


2.4 RW 操纵律
考虑内转子的转速均衡及能量消耗,得控制目标函数

式中:W2,Z为正定加权阵;为目标转子角加速度,且

式(19)中,Ωd为需逼近的目标转子转速,取其为转子转速的均值。
在目标函数中引入Lagrange乘子向量λ2,有

L2()的极小值条件为

则可得内转子的


式(16)、(17)、(22)、(23)即为两 VSDGCMG操纵律。
3 仿真分析


图3 VSDGCMG 1外框架角Fig.3 Angular of outer gimbals of VSDGCMG 1
由仿真结果可知:本文的两VSDGCMG操纵律能保证VSDGCMGs的输出力矩跟踪姿态控制指令力矩,在输出力矩的过程中,VSDGCMG的框架角速度平滑变化,降低了伺服电机的控制难度。
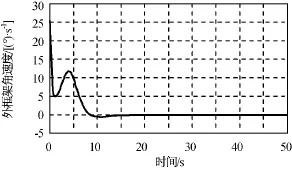
图4 VSDGCMG 1外框架角速度Fig.4 Angular velocity of outer gimbals of VSDGCMG 1

图5 VSDGCMG 2外框架角Fig.5 Angular of outer gimbals of VSDGCMG 2

图6 VSDGCMG 2外框架角速度Fig.6 Angular velocity of outer gimbals of VSDGCMG 2

图7 VSDGCMG 1内框架角Fig.7 Angular of inner gimbals of VSDGCMG 1

图8 VSDGCMG 1内框架角速度Fig.8 Angular velocity of inner gimbals of VSDGCMG 1

图9 VSDGCMG 2内框架角Fig.9 Angular of inner gimbals of VSDGCMG 2

图10 VSDGCMG 2内框架角速度Fig.10 Angular velocity of inner gimbals of VSDGCMG 2

图11 指令力矩Fig.11 Order torques

图12 输出力矩Fig.12 Output torques
4 结束语
本文研究了平行构型VSDGCMG的操纵律设计及实现。综合了平行构型的优点和控制力矩陀螺转子的可变速性的特点,将每一对框架轴平行的VSDGCMG作为独立的单元控制。引入与陀螺框架运动相关的动坐标系,在构型奇异状态下仍可控,且无力矩误差。该控制算法简单,易于工程实现。
[1] 王 磊,赵育善,李 云.平行构型双框架控制力矩陀螺操纵律研究[J].宇航学报,2009,30(4):1551-1563.
[2] 杨 倩,崔培玲,韩邦成,等.航天器机动时DGMSCMG磁悬浮转子干扰补偿控制[J].宇航学报,2012,33(6):720-727.
[3] 段洪栋,吴 忠.基于磁悬浮控制力矩陀螺的航天器动力学与仿真[J].系统仿真学报,2009,21(9):2783-2790.
[4] YEONKYU K,RAYMOND B,PALAZZOLO A,et al.Interactions dynamics between a satellite and onboard magnetically suspended flywheels[C]//1st International Energy Conversion Engineering Conference.Portsmouth:AIAA,2003:6109.
[5] AHRENS M,KUCERA L,LARSONNEUR R.Performance of a magnetically suspended flywheel energy storage device[J].IEEE Transactions on Control Systems Technology (S1063-6536),1996,4(5):494-501.
[6] 魏 彤,房建成,刘珠荣.双框架磁悬浮控制力矩陀螺动框架效应补偿方法[J].机械工程学报,2010,46(2):159-165.
[7] 贾英宏,徐世杰.采用平行构型变速控制力矩陀螺群的航天器姿态控制[J].宇航学报,2003,24(5):490-495.
[8] 汤 亮,徐世杰.采用变速控制力矩陀螺的航天器自适应姿态跟踪和稳定控制研究[J].航空学报,2006,27(4):663-669.

