干摩擦悬臂梁一阶等效固有频率研究
第一作者赵峰男,博士生,1987年生
通信作者曹树谦男,博士,教授,1964年生
干摩擦悬臂梁一阶等效固有频率研究
赵峰1,2,3,曹树谦1,2,3,冯文周1,2,3(1.天津大学机械工程学院,天津300072;2. 天津市非线性动力学与混沌控制重点实验室,天津300072;3. 内燃机燃烧学国家重点实验室,天津300072)
摘要:采用牛顿第二定律及拉格朗日方程,分别对干摩擦悬臂梁及等效模型建立振动控制方程,获得两种模型的激励力与频率关系式,基于能量相等建立等效方程进行一阶等效固有频率研究,获得干摩擦悬臂梁等效固有频率解析表达式。采用数值方法计算干摩擦悬臂梁模型一阶固有频率。结果表明,数值与解析结果一致性较好,即悬臂梁等效固有频率随干摩擦增大而减小。所得解析表达式能更直接获得干摩擦力对悬臂梁固有频率影响规律。
关键词:干摩擦;悬臂梁;固有频率;等效法
基金项目:天津市自然科学基金重点项目(11JCZDJC25400); 齐齐哈尔轨道交通装备有限责任公司项目(2011GFW-0663)
收稿日期:2014-03-12修改稿收到日期:2014-05-08
中图分类号:O322文献标志码:A
First order equivalent natural frequency for a cantilever beam with dry friction
ZHAOFeng1,2,3,CAOShu-qian1,2,3,FENGWen-zhou1,2,3(1. School of Mechanical Engineering, Tianjin University, Tianjin 300072, China;2.Tianjin Municipal Key Laboratory of Nonlinear Dynamics and Chaos Control, Tianjin 300072, China; 3.State Key Laboratory of Engines, Tianjin University, Tianjin 300072, China)
Abstract:Here, the first order natural frequency of a cantilever beam with dry friction was studied using an equivalent method. The motion equations of the beam and its equivalent model were established using Newton’s second law and Lagrange equation, respectively. Then, the relationships between excitation force and natural frequency of the two models were obtained. Base on the idea of inputting same energy, using the equivalent method, an analytical expression for the first order equivalent natural frequency of the cantilever beam with dry friction was derived. The numerical method for calculating the first order natural frequency of the beam was used to verify the effectiveness of the equivalent method. The results showed that the first order natural frequencies obtained with the numerical method and the analytical expression agree well under different dry frictions, the first order equivalent natural frequencies decrease with increase in dry friction; furthermore, the analytical expression for the first order equivalent natural frequency of the beam can directly reflect the effect law of dry friction on the first order natural frequency of the cantilever beam.
Key words:dry friction; cantilever beam; natural frequency; equivalent method
机械系统中干摩擦作为重要的阻尼资源,对系统振动影响颇受关注[1],并广泛用于航空发动机转子叶片、货车转向架摇枕侧架及其它结构[2]。在机械结构中,干摩擦能快速有效抑制因外部扰动致系统产生的动力学响应[3-4],而干摩擦因素对系统动态固有特性影响关注较少。目前,非线性模态概念较难用于干摩擦结构振动固有特性研究[5-6];而数值方法不能给出简单直观的解析式。因此基于等效思想,用解析方法探索库仑干摩擦力对悬臂梁固有频率影响规律[7-9]不失为可行的研究方法。
研究系统固有频率等效方法一般包括微分方程法、能量法及静变形法。本文采用微分方程法[7]及能量法[10-13]研究悬臂梁固有频率受横向干摩擦因素的影响规律。对此已有研究涉及,如基于单自由度质量弹簧模型为等效对象,文献[14-16]简略介绍求解非线性系统固有频率等效思想;文献[17-18]研究纵向干摩擦力对悬臂梁振动特性影响,未涉及系统固有频率解析表达式及干摩擦力对固有频率影响规律研究。
本文采用牛顿第二定律及拉格郎日方程,分别建立干摩擦悬臂梁模型及悬臂梁等效模型运动方程,通过等效思想求得干摩擦悬臂梁固有频率解析式;并采用数值方法对一阶等效固有频率解析式进行数值验证。结果表明,数值解与解析解一致较好性,故用于研究干摩擦力对悬臂梁振动固有特性影响规律。本文方法为干摩擦影响下机械结构固有振动特性研究提供可行的解析方法。
1模型运动方程
以自由端具有干摩擦阻尼的均质悬臂梁为研究对象,见图1。系统阻尼为干摩擦,摩擦接触点在z2处,干摩擦阻尼由摩擦界面法向压力FN产生。采用牛顿第二定律建立运动方程,并求解方程的力频(谐波激励力F与固有频率)关系。
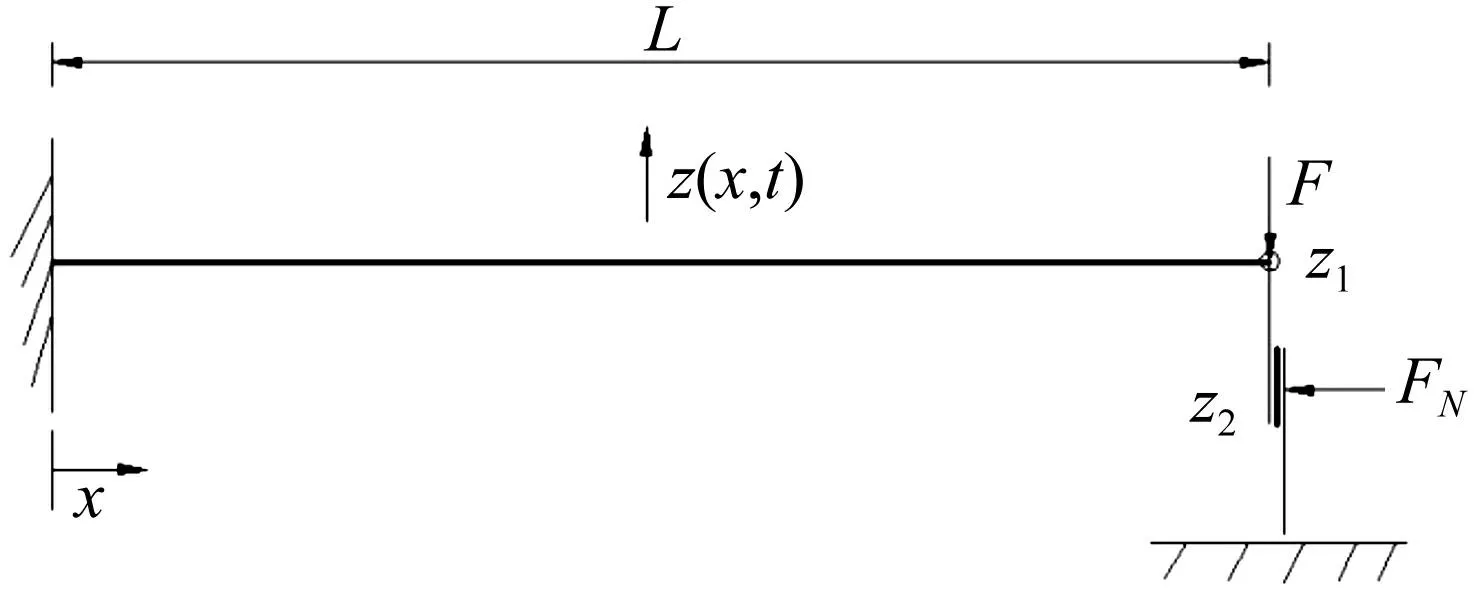
图1 干摩擦悬臂梁 Fig.1 Model of cantilever beam with dry friction
据牛顿第二定律,运动方程可写为
(1)
式中:m(x)为梁单位长度质量;w(x,t)为梁横向振动位移;F(x,t)为梁自由端点激振力(作用于z1点);FN为摩擦界面法向压力;EI(x)为梁抗弯刚度;μ为摩擦界面库仑摩擦系数。
对式(1)用一阶伽辽金近似,设梁位移表达式为
w(x,t)=z(t)φ(x)
(2)
将式(2)代入式(1),进行伽辽金过程产生等效单模态模型(设φL=φ(L)>0,悬臂梁自由端振型值)为

式中:mn,mnωn2,f(t)分别为模态质量、模态刚度及力函数。
设模态幅值与模态力函数为
z(t)=Acos(ωt)
(4)
f(t)=fccos(ωt)+fssin(ωt)
(5)
对不连续的符号函数连续化处理,即对符号函数进行傅里叶级数展开,并取一阶项为
sgn(-Aωsin(ωt))≈-(4/π)sin(ωt)
(6)
将式(4)、(5)、(6)代入式(3),平衡一次谐波项系数,整理得
(7)
式中:fc为激励力余弦力幅值;fs为激励力正弦力幅值。
式(7)为由干摩擦悬臂梁模型推导所得激励力正、余弦幅值与系统固有频率关系(激励力与悬臂梁固有频率关系,简称力频关系)。
2等效模型运动方程
据激励能量相等原理建立等效模型,见图2,等效模型物理、结构参数同图1。
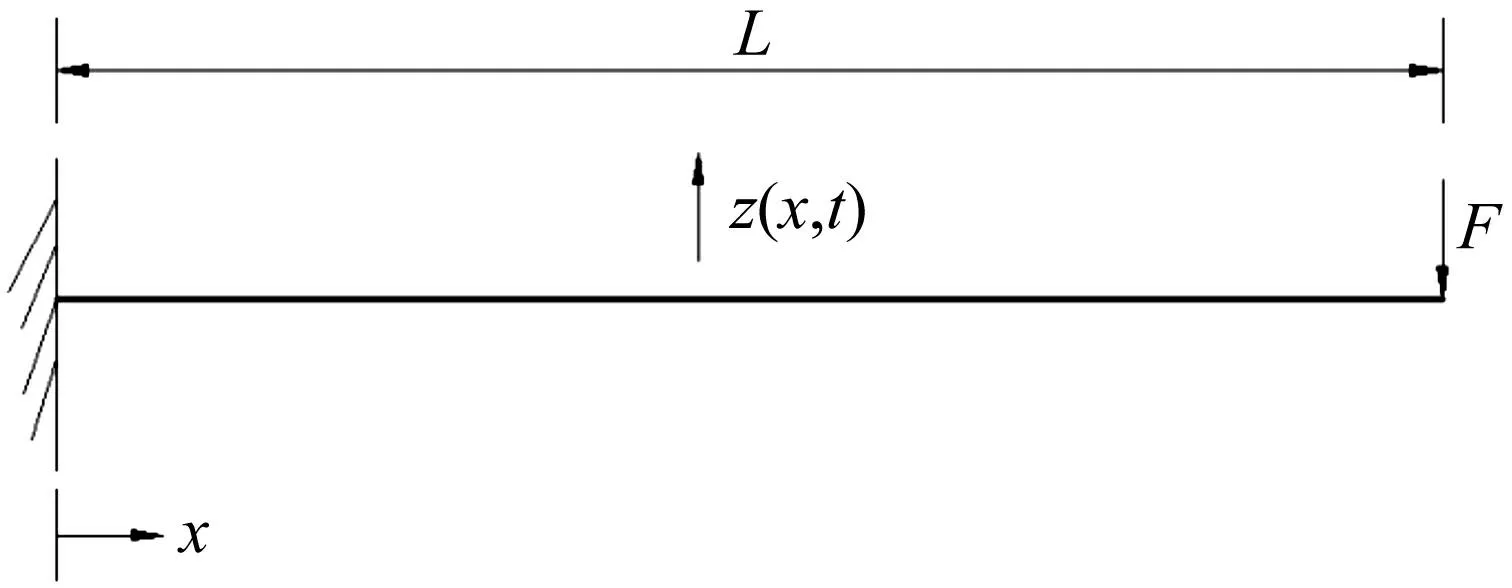
图2 等效悬臂梁 Fig.2 Equivalent model of cantilever beam with dry friction
考虑悬臂梁阻尼特性,采用拉格朗日第二类方程建立等效模型运动方程。悬臂梁系统动能为
(8)
式中:ai为梁广义坐标;Mi为梁广义质量。
悬臂梁模型势能与系统耗散能为
(9)
(10)
式中:ωi为悬臂梁第i阶固有频率;ζi为悬臂梁第i阶阻尼。
激励力所做虚功为
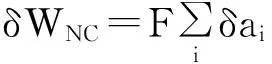
(11)
式中:F为外部激励力;xF为激励力F作用位置。
拉格朗日函数为
L=T-V=
(12)
由此得拉格朗日运动方程为

(13)
式(13)中假设模态函数为
a(t)=Acos(ωt)
(14)
式中:A为幅值;ω为振动频率。
式(13)中假设模态激励力函数为
F(t)=Fccos(ωt)+Fssin(ωt)
(15)
式中:Fc为余弦激励力部分;Fs为正弦激励力部分。
将式(14)、(15)代入式(13),平衡一阶谐波项系数、化简整理,并为便于区分等效固有频率与悬臂梁固有频率,令方程中干摩擦作用后悬臂梁等效固有频率Ωi=ωi,对等效模型运用拉格朗日方程及谐波平衡法建立力频关系式为
(16)
3固有频率解析式
干摩擦力会对系统的振动特性产生影响[19]。悬臂梁受干摩擦力后,其固有振动特性变化,本文将用激励能量等效方法进行研究。令干摩擦悬臂梁正、余弦力fs、fc与无干摩擦悬臂梁正、余弦力Fs、Fc相等及n=i=1,可得干摩擦悬臂梁第一阶等效固有频率。消去激励频率ω,整理并化简得
(17)
式中:Ω1为干摩擦悬臂梁第一阶等效固有频率。
将式(17)进一步简化,令M1=m1,摩擦力fd=μFN。等效表达式中,为保证无干摩擦条件下等效固有频率解析值与线性固有频率相等,令等效固有频率线性项部分φi(xF)=1,得等效固有频率简化表达式为
(18)
式中:ω1为悬臂梁第一阶固有频率。
4数值验证
图1、图2模型悬臂梁结构参数见表1。

表1 悬臂梁结构参数
对式(3)进行数值计算,验证一阶等效固有频率解析式的正确性。在不同干摩擦力下用快速傅里叶变换,获得系统响应频域曲线,计算曲线峰值即得各干摩擦力工况系统一阶固有频率数值解,并与解析值比较,以达验证解析式目的。令f(t)=0,模态阶数n=1,则方程(3)为
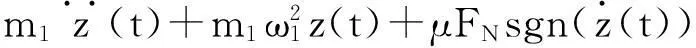
(19)
式中:m1=3.12;ω1=8.38;φ1(L)=1.1322;μFN为干摩擦力幅值(表2)。
将每个干摩擦力幅值代入方程(19),计20个工况,对每种工况进行数值计算,获得不同干摩擦工况下一阶固有频率值。以位移1 mm、速度0 mm/s为初始条件,设置采样频率fs=100 Hz,采样点N=1024。对响应位移信号(或速度信号)用快速傅里叶变换获得频域曲线,取曲线峰值即可得一阶固有振动频率[20-21]。20种干摩擦力工况所得悬臂梁一阶固有频率见表2。
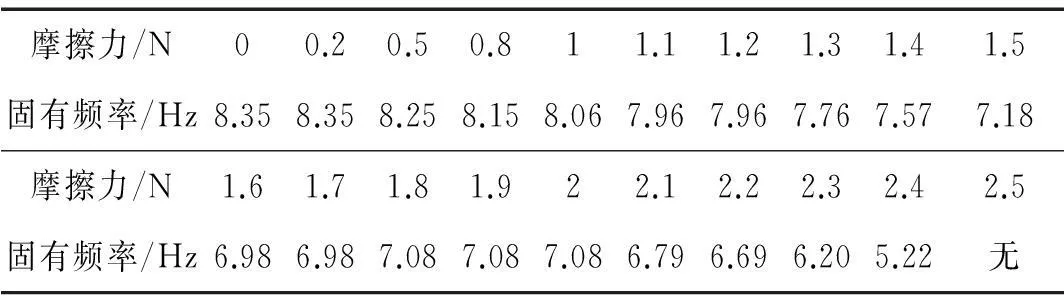
表2 不同干摩擦力工况下悬臂梁一阶固有频率
将表2中不同干摩擦工况一阶固有频率数值解(图3离散点)与解析式(18)的解析值(图3实线)对比发现,两种方法所得结果吻合度较高,实线与离散点变化趋势基本一致,即随干摩擦力增大一阶固有频率降低。因此,数值计算方法验证了一阶等效固有频率解析表达式的正确性与有效性。由图3看出,当干摩擦力在0~1 N时两种方法所得一阶固有频率偏差很小,且在此阶段系统固有频率受干摩擦力影响较小;干摩擦力在1~2.5 N之间时两种方法所得一阶固有频率偏差较高,且干摩擦力对固有频率影响较大。由数值解、解析解发现,随干摩擦力增大一阶固有频率呈整体下降趋势;数值结果呈非单调性,而解析结果随干摩擦力增大单调递减。此因解析过程中,通过一次傅里叶近似将库仑干摩擦力模型光滑化。
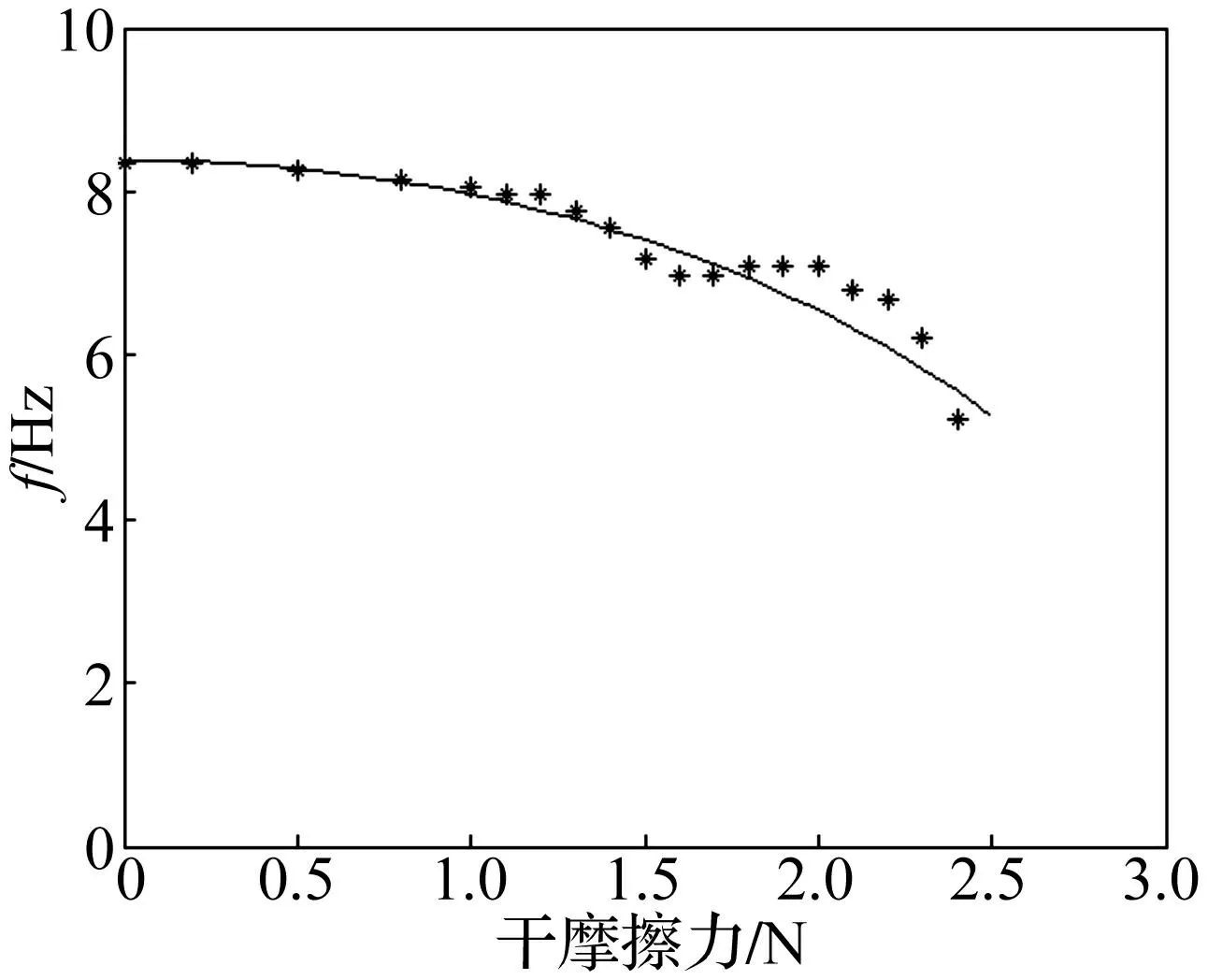
图3 解析一阶等效固有频率(实线) 与数值一阶固有频率(离散点) Fig.3 First-order equivalent natural frequency of analytic method (solid line) and numerical method (discrete points)

图4 阻尼对等效一阶固有频率影响 (三种不同大小阻尼) Fig.4 Influence of damping on the first order equivalent natural frequency (three different damping)
式(18)中等效悬臂梁阻尼参数ζ1为给定,按已给阻尼参数所得解析结果与数值方法所得结果最佳逼近原则给定阻尼参数为0.011。整体上阻尼参数对解析值变化趋势无影响,但对具体结果有影响,给定不同阻尼所得解析值也不同。阻尼增大或减小时对等效频率影响见图4。以阻尼为0.011的等效固有频率曲线为基准,阻尼增大时等效固有频率曲线向上偏移;阻尼减小时等效固有频率曲线向下偏移。
5结论
(1)采用牛顿第二定律对干摩擦悬臂梁模型建立运动方程,运用拉格郎日第二方程建立等效模型运动方程,基于激励能量相等原理求得干摩擦悬臂梁第一阶等效固有频率解析解表达式并进行数值验证。结果表明解析值与数值解一致性较好。解析式能直观反映悬臂梁固有频率受干摩擦力影响规律。
(2)法向压力只产生干摩擦阻尼力,对梁的刚度无影响。结构仅受干摩擦阻尼力影响,梁固有频率亦仅受非线性阻尼影响。
(3)一阶固有频率解析值与数值解均表明,随干摩擦力幅值增大悬臂梁固有频率逐渐降低。因干摩擦力函数光滑化,解析值具有单调下降特点;数值运算中未对符号函数进行处理,数值解具有非单调特性。干摩擦力幅值较小时对悬臂梁固有频率基本无影响;干摩擦力较大时悬臂梁固有频率下降幅度较大。此对干摩擦结构设计具有指导意义。
参考文献
[1]Den Hartog J P. Forced vibrations with combined viscous and coulomb damping[J]. Phil.Mag.S.7, 1930,59(9): 801-817.
[2]赵峰,曹树谦,于跃斌,等. 干摩擦双层梁的工作模态实验方法[J]. 振动、测试与诊断, 2013, 33(6): 971-976.
ZHAO Feng, CAO Shu-qian, YU Yao-bin, et al. The experimental method study of operating modal analysis on a double beam model with dry friction[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(6): 971-976.
[3]贾尚帅,丁千. 刹车系统的摩擦自激振动和控制[J]. 工程力学, 2012(3): 252-256.
JIA Shang-shuai, DING Qian. Friction-induced self-excited vibration and control of a brake system[J]. Engineering Mechanics, 2012(3): 252-256.
[4]丁千,陈予恕. 转子碰摩运动的非稳态分析[J]. 航空动力学报, 2000(2): 191-195.
DING Qian, CHEN Yu-shu. Non-stationary analysis of rotor/casing rubbing [J]. Journal of Aerospace Power, 2000(2): 191-195.
[5]陈予恕,吴志强. 非线性模态理论的研究进展[J]. 力学进展, 1997, 27(3): 289-299.
CHEN Yu-shu, WU Zhi-qiang. Advances in study on theories of nonlinear normal modes [J]. Advances in Mechanics, 1997, 27(3): 289-299.
[6]Vakakis A F, Bergman L A, McFarland D M, et al. Current efforts towards a non-linear system identification methodology of broad applicability[J]. Proceedings of the Institution of Mechanical Engineers[C]. Journal of Mechanical Engineering Science, 2011: 1-19.
[7]Whiteman W E, Ferri A A. Displacement-dependent dry friction damping of a beam-like structure[J]. Journal of Sound and Vibration, 1996, 198(3): 313-329.
[8]严天宏,郑钢铁,黄文虎. 由摩擦阻尼铰实现桁架结构的被动减振研究[J]. 航空学报, 1999, 20(1): 17-21.
YAN Tian-hong, ZHENG Gang-tie, HUANG Wen-hu. Research on passive vibration control of truss structures by displacement-dependent dry frictional joints[J]. Acta Aeronauticaet Astronautica Sinica, 1999, 20(1): 17-21.
[9]Ren Y S, Qin H Z, Zhao Z L. Nonlinear vibration analysis of a beam with dry friction at the supports[J]. Mechanics Research Communications, 1999, 26(1): 83-89.
[10]Ferri A A, Dowell E H. Frequency domain solutions to multi-degree-of-freedom, dry friction damped systems[J]. Journal of Sound and Vibration, 1988, 124(2): 207-224.
[11]Dowell E H, Schwartz H B. Forced response of a cantilever beam with a dry friction damper attached, part 1: theory[J]. Journal of Sound and Vibration, 1983, 91(2): 255-267.
[12]Young J G, Kim Y H, Chang H G. An analysis of the behavior of a simply supported beam with a dry friction damper attached[J]. Applied Acoustics, 1998, 55(1): 31-41.
[13]郝淑英,陈予恕,张琪昌. 连接结构松动对系统非线性动力学特性的影响[J]. 天津大学学报, 2001, 34(4): 452-454.
HAO Shu-ying, CHEN Yu-shu, ZHANG Qi-chang. Effects of connect loosing and sliding on dynamic characteristics[J]. Journal of Tianjin University, 2001, 34(4): 452-454.
[14]Ferri A A, Whiteman W E. Free response of a system with negative viscous damping and displacement-dependent dry friction damping[J]. Journal of Sound and Vibration, 2007, 306: 400-418.
[15]Ostachowicz W M. A discrete linear beam model to investigate the nonliear effects of slip friction[J]. Computer and Structures, 1990, 36(4): 721-728.
[16]Poudou O J. Modeling and analysis of the dynamics of dry-friction-damped structural systems[D]. USA:University of Michigan, 2007.
[17]Dowell E H. The behavior of a linear, damped modal system with a non-linear spring-mass-dry friction damper system attached[J]. Journal of Sound and Vibration, 1983, 89(1): 65-84.
[18]Dowell E H. Damping in beams and plates due to slipping at the support boundaries[J]. Journal of Sound and Vibration, 1986, 105(2): 243-253.
[19]Kerschen G, Worden K, Vakakis A F, et al. Past, present and future of nonlinear system identification in structural dynamics[J]. Mechanical Systems and Signal Processing, 2006, 20(3): 505-592.
[20]丁虎, 张国策, 陈立群. 超临界轴向运动梁横向非线性振动频域分析[J]. 固体力学学报, 2011, 32(4): 360-363.
DING Hu, ZHANG Guo-ce, CHEN Li-qun. Frequency domain analysis of supercritical nonlinear vibration of axially moving beams[J]. Chinese Journal of Solid Mechanics, 2011, 32(4): 360-363.
[21]佟德纯. 设备故障诊断技术讲座,第四讲:机械设备振动特征分析[J]. 振动与冲击, 1993, 12(2): 70-78.
TONG De-chun. Lectures of diagnostic techniques of Equipment failures, the fourth section: vibration characteristics analysis of mechanical equipments [J]. Journal of Vibration and Shock, 1993, 12(2): 70-78.



