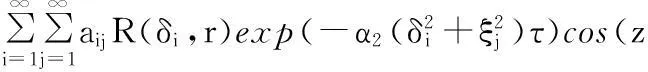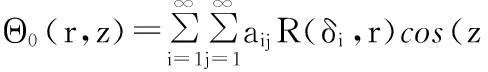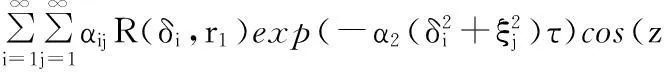热态轴类含空洞锻件内部温度场分布

热态轴类含空洞锻件内部温度场分布

张玉存1张雷强1付献斌2

1.燕山大学,秦皇岛,0660042.中国环境管理干部学院,秦皇岛,066102

摘要：热态轴类锻件内部温度场分布特征对锻件内部空洞检测起着重大作用。针对该问题，在传热学理论的基础上建立了热态轴类含空洞锻件的二维非稳态传热模型。首先利用集总参数法获得该模型的内部边界条件。然后通过红外热像仪采集得到该模型的初始温度条件，结合分离变量法求解该模型，从而获得含空洞锻件的内部温度场分布。最后通过实验分析了不同空洞尺寸条件下锻件内部温度场的分布特征。

关键词：空洞检测；二维非稳态传热；内部温度场；热态轴类锻件

中图分类号：TG157

收稿日期：2015-01-06

基金项目：河北省自然科学基金资助项目(E2014203070)

作者简介：张玉存，男，1969年生。燕山大学电气工程学院教授、博士。主要研究方向为信号处理与识别、测试技术、故障诊断等。发表论文20余篇。张雷强，男，1988年生。燕山大学电气工程学院硕士研究生。付献斌，男，1985年生。中国环境干部管理学院信息工程系讲师。

Analyses of Interior Temperature Field Distribution for Hot Axial Forgings with Void

Zhang Yucun1Zhang Leiqiang1Fu Xianbin2

1.Yanshan University，Qinhuangdao，Hebei，066004

2.Environmental Management College of China，Qinhuangdao，Hebei，066102

Abstract:For hot axial void forgings, interior temperature field distribution plays a key role in the detection of inner void defect. Aiming at the issue, a two-dimensional unsteady heat transfer model of the forgings with void was established based on the heat transfer theory. Firstly, interior boundary conditions of the model were obtained by using lumped parameter method. Secondly, the initial temperature conditions of the model were collected by the thermal infrared imager. The interior temperature field distribution of forgings with void was acquired by separation variable method. Finally, interior temperature field distribution characteristics of forgings under different void size conditions were analyzed according to the experimental results.

Key words: void detection; two-dimensional unsteady heat transfer; interior temperature field; hot axial forgings

0引言

热态轴类锻件是电力、石油行业和大型机器装备的核心部件，其质量的好坏是一个国家工业水平的重要体现。空洞缺陷的存在往往会引起空洞边界处锻件材料的破坏[1-2]。通过研究含空洞锻件内部温度场分布特征，发现锻件内部空洞缺陷，对提高锻件成形质量具有重要意义。

在含有内部缺陷物体的温度场分布特征研究方面，文献[3]利用红外扫描技术对物体内部缺陷温度场的形成及其演变规律进行了实验研究。文献[4-5]通过实验和有限元仿真，研究了复合材料内部缺陷尺寸对其表面温度场分布的影响规律。文献[6]通过有限体积法对具有矩形内部缺陷试件的温度场进行了求解，分析了试件检测表面的温度分布规律。文献[7]在单面法加热的基础上，通过数值计算分析了二维钢板模型随其内部缺陷长度、深度变化的规律，得到了钢板表面温度场的分布特征。文献[8]以铝铸件内部空洞检测为研究对象，借助有限元分析软件COMSOL得到了空洞大小、位置变化时的铸件表面温度场分布情况。以上研究都是通过分析物体表面温度场来实现对内部缺陷检测的，但随着缺陷深度的增大，单纯依靠分析表面温度场的分布特征难以实现对缺陷的精确检测，因而，如何获取及分析靠近物体缺陷区域的内部温度场分布，进而获取精确的内部缺陷尺寸信息就成为一个亟待解决的问题。

本文是在二维非稳态传热的基础上建立轴类含空洞锻件传热模型，利用集总参数法和分离变量法获得不同内部空洞尺寸下的锻件内部温度场分布，通过全面分析锻件内部传热变化特征，发现了空洞缺陷存在时锻件内部特有的温度场分布规律。

1轴类含空洞锻件内部温度场分布模型

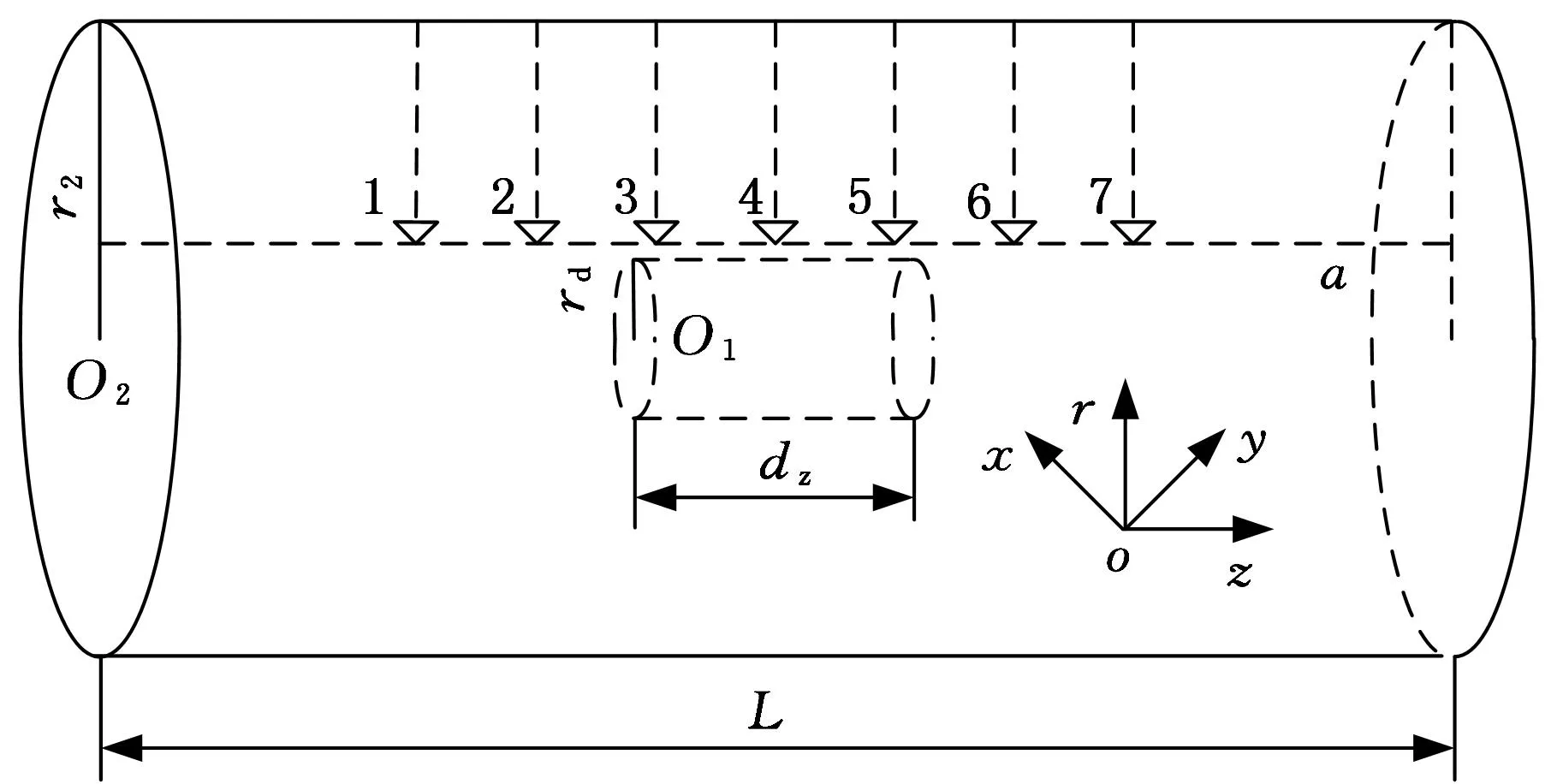
轴类含空洞锻件模型如图1所示。图1中，圆柱形空洞位于该锻件的中心位置附近。本文将锻件中的空洞与锻件材料视为两种不同的传热介质。

图1　轴类含空洞锻件模型

首先对含空洞锻件进行研究，由于锻件内部空洞部分相对于整个锻件较小，空洞内部温度分布比较均匀，并且空洞与无空洞部分的比奥数均小于0.1，因此含空洞锻件的热传导过程满足集总参数法的使用条件。根据集总参数法，空洞和锻件无空洞部分的能量平衡关系式分别为

(1)

(2)

式中，ρ、c、V、A、T分别为密度、比热、体积、外侧表面积和温度场函数，且T≡T(r, z, τ)，下标1、2分别表示空洞和锻件无空洞部分；h1为空洞与无空洞部分的换热系数；h2为无空洞部分与外界周围环境的换热系数；Tw为环境温度；τ为时间变量。

令K1=h1A1/(ρ1c1V1)，K2=h1A1/(ρ2c2V2)，K3=h2A2/(ρ2c2V2)。根据初始条件即τ=0时，dT1/dτ=0，可获得T1(τ)最终的解：

(3)

(4)

ζ2=

(5)

式中，T0为锻件初始温度。

由于柱体具有轴对称性，因此，圆柱锻件非空洞部分传热问题可简化为柱坐标系下的二维热传导问题。采用圆柱坐标系对模型中锻件的无空洞部分建立导热微分方程：

(6)

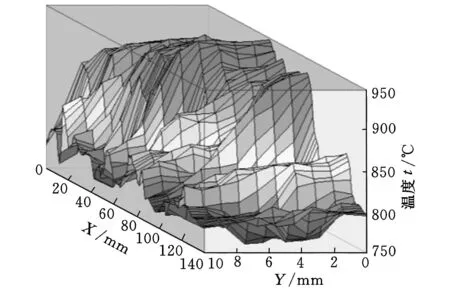
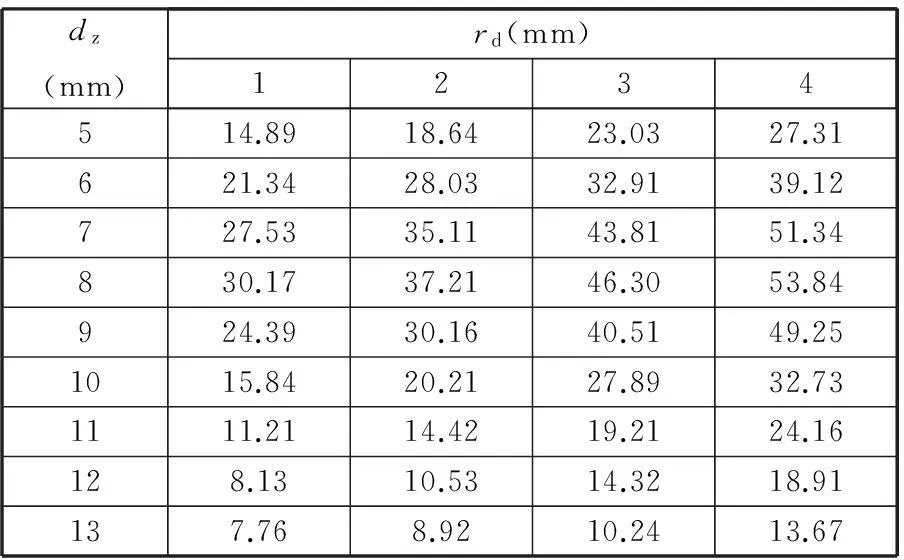
r1

式中，z为柱坐标系中的坐标轴；α2为圆柱锻件外壁的热扩散系数。

将得到的空洞平均温度T1(τ)作为锻件无空洞部分的内部边界温度，可得空洞以外介质的内部边界条件：

(7)

r=r1τ>0

忽略轴类锻件端部传热，则锻件空洞以外介质的外部边界条件为

(8)

由红外热像仪获得的传热模型初始温度条件为

T2=T0(r,z)

(9)

r1≤r≤r2,τ=0

式中，k2为空洞以外介质的热传导系数；r1、r2分别为空洞和圆柱锻件的半径；d1、d2分别为柱形空洞上下表面与圆柱锻件底面的距离；d3为圆柱锻件的高度。

为使边界条件齐次化，令

Θ(r，z，τ)=T2(r，z，τ)-Tw

(10)

采用分离变量法对Θ(r，z，τ)进行求解。把Θ(r，z，τ)分离成以下形式：

Θ(r，z，τ)=R(r)Z(z)Π(τ)

(11)

式(11)中分离变量Π(τ)的分离方程为

(12)

式(12)的基础解系由exp(-α2σ2τ)构成。

分离变量R(r)的分离方程为

(13)

式(13)的基础解系由第一类贝塞尔函数J0(δr)和第二类贝塞尔函数Y0(δr)构成。

分离变量Z(z)的分离方程为

(14)

式(14)的基础解系由sin(zξ)和cos(zξ)构成，其中，ξ2=σ2-δ2，σ、δ为待定参数。为满足圆柱锻件上下底的边界条件，式(14)的基础解应舍去sin(zξ)，只取cos(zξ)，且ξ的取值只能是ξj=nπ/d3，n=1，2，…。

由式(12)～式(14)的基础解叠加构成Θ(r，z，τ)的完全解：

Θ(r,z,τ)=

(15)

由初始条件可得

T0(r,z)-Tw

(16)

根据相关函数的正交性可得

(17)

为满足式(13)及锻件外侧壁边界条件，R(δi，r)可取

R(δi，r)=PY0(δir)-QJ0(δir)

(18)

P=SJ0(δir2)+δiJ1(δir2)

Q=SY0(δir2)+δiY1(δir2)

S=-h2/k2

将式(18)代入锻件内部边界条件可得

T1(τ)-Tw

(19)

由式(19)可确定δi的值。

根据式(10)、式(15)～式(17)，最终获得含空洞锻件内部温度场分布：

T2(r,z,τ)=Tw+

(20)

2实验研究

本实验首先利用超声波探伤技术检测圆柱锻件，选取内部不含缺陷的锻件；之后根据实验所需要的锻件内部空洞直径，选取相同直径的钻头对无缺陷锻件两端圆心处进行钻孔直至打通；然后利用与钻孔锻件具有相同材料的圆柱体对锻件两端钻孔进行填补，空洞的长度根据填补材料的长度而定；最后利用焊接技术对圆柱体与钻孔之间的缝隙进行填补，同时再次使用超声波探伤技术对填补后锻件进行检测，直到锻件内部只有柱形空洞缺陷为止。圆柱锻件钻孔及填补完成的锻件分别为图2、图3所示。

图2　圆柱锻件钻 图3　圆柱锻件 　　孔完成图 　填补完成图

为了研究含空洞锻件内部温度场的分布特征，将上述方法制备的含空洞轴类锻件作为实验锻件，如图4所示，其中，L=600mm，r2=100mm。图4所示锻件内部含有一个圆柱形空洞，其中，rd为空洞半径，dz为空洞的长度，且该空洞的底边圆心位于锻件横轴中心线上，实验材料的热物理参数如表1所示。锻件内部虚线a为实验研究对象，为了使得锻件内部层a上温度场分布能够更加准确地反应空洞尺寸变化情况，令每组实验中选取的锻件内部虚线a都为非常接近空洞表面的锻件内部层。

图4　含空洞锻件示意图

对比对象锻件无空洞部分空洞部分材料类型45钢空气热传导系数k(W/(m·K))26.490.023质量热容c(J/(kg·K))806103密度ρ(kg/m3)78501.293

首先将该锻件置于SRJX-8-13箱式电阻炉内加热，待加热至1000℃时停止加热，将该锻件取出置于所处环境温度为20℃的滚动台上，将事先调试好的红外热像仪对锻件进行检测。实验装置如图5所示。此时锻件表面温度场可被准确获取，锻件表面某时刻的3D温度场分布情况如图6所示。

图5　实验装置图

图6　锻件表面3D温度场分布

(1)第一组实验。该组实验选取锻件内部层a上7个点作为检测对象，如图4所示。选取t=600s为研究时间点，dz长度为8mm不变，当空洞半径rd改变时，根据含空洞锻件的内部温度场分布模型可准确获得锻件内部层a上7点在同一时刻的温度值，内部层a上7点的温度分布情况如表2所示。

表2　第一组实验数据　℃

运用MATLAB分别对表2中含空洞锻件内部7处温度测量值进行拟合，拟合曲线如图7所示。由图7可知，锻件内部空洞垂直上方对应的内部层区域温度低于内部层上非空洞对应区域的温度，且随着空洞半径的增大，空洞对应的内部层区域温度逐渐降低。这是由于空洞的热传导系数比锻件小得多，阻止了热量向空洞对应内部层区域的传递，并且这种阻止能力会随着空洞半径的增大而增大，最终导致空洞对应内部层区域温度的降低。

图7　同一时刻不同空洞半径时锻件内层7点的温度分布

(2)第二组实验。同样选取t=600s作为研究时间点，当rd和dz取不同值时，空洞垂直对应的内部层上最大温差ΔTmax如表3所示。

运用MATLAB分别对表3中数据进行拟合，拟合曲线如图8所示。由图8可知，空洞半径越大，空洞对应内部层区域的温差越大，由此说明较大空洞所对应内部层区域温度较低；锻件空洞对应内部层区域的最大温差随着空洞长度的增加

表3　第二组实验数据　℃

先增大后减小，且存在一个极值点。由此说明内部层各点温度是随空洞的长度增加而减小的，当空洞的长度增大到一定值时，空洞尺寸将影响到整个内部层的温度分布，使得内部层温度整体下降，从而导致内部层最大温差减小，可检测性下降。

图8　锻件内部层上最大温差分布图

另外，在以上的两组实验研究中，锻件内部层上各点的温度数据是通过将内部层上各点的位置信息和空洞的尺寸信息以及由红外热像仪测得的锻件初始温度信息代入式(20)中来求得的。

3结论

(1)锻件内部空洞垂直上方对应的内部层区域温度低于内部层上非空洞对应区域的温度。

(2)当锻件内部空洞长度不变时，空洞垂直上方对应的内部层区域温度随着空洞半径的增大而逐渐降低。

(3)当锻件内部空洞半径不变时，空洞垂直上方对应的内部层区域最大温差随着空洞的长度的增加先增大后减小，且存在一个极值点。

参考文献：

[1]任运来, 聂绍珉, 牛龙江, 等. 大型锻件内部空洞缺陷修复条件[J]. 机械工程学报, 2008 , 44(2): 248-252.

Ren Yunlai, Nie Shaomin, Niu Longjiang, et al. Healing Conditions of Large Forgings Internal Voids Defect[J]. Chinese Journal of Mechanical Engineering, 2008, 44(2): 248-252.

[2]张效迅. 大锻件锻造成形过程中内部空洞型缺陷演化规律的研究[D]. 上海: 上海交通大学, 2009.

[3]李之达. 缺陷演化过程中缺陷温度场的实验研究[J]. 实验力学, 1997, 12(3): 370-375.

Li Zhida. Experimental Research on Defect Temperature Field in Process of Defect Evolution[J]. Journal of Experiment Mechanics, 1997, 12(3): 370-375.

[4]郑恩辉, 曹文浩, 富雅琼, 等. 缺陷表面温度场的红外无损检测分析[J]. 计算机仿真, 2013, 30(4): 416-420.

Zheng Enhui, Cao Wenhao, Fu Yaqiong, et al. Analysis of Temperature Field on Near Surface Defect in Infrared Nondestructive Testing[J]. Computer Simulation, 2013, 30(4): 416-420.

[5]葛孚宁. 基于红外测温的设备内部缺陷诊断[J]. 机电工程技术,2008, 37(7): 36-38.

Ge Funing.Internal Defects Diagnosis of the Equipment Based on Infrared Thermometry[J]. Mechanical & Electrical Engineering Technology, 2008, 37(7): 36-38.

[6]王海亮, 范春利, 孙丰瑞, 等. 二维内部缺陷的红外瞬态定量识别算法[J]. 红外与激光工程, 2012, 41(7): 1714-1720.

Wang Hailiang, Fan Chunli, Sun Fengrui,et al. Transient Quantitative Infrared Thermographic Identification of Two-dimensional Inner Defect[J]. Infrared and Laser Engineering，2012，41(7)：1714-1720.

[7]沈丽华, 孙丰瑞, 杨立, 等. 单面法红外检测钢板内壁缺陷温度场研究[J]. 激光与红外, 2006, 36(1): 19-22.

Shen Lihua, Sun Fengrui Yang Li, et al. Study on Temperature Distribution Rule of Steel Plate with Inner Surface Defect Inspected Single-sided Thermography[J]. Laser & Infrared, 2006, 36(1): 19-22.

[8]赵景媛, 王黎明, 刘宾. 铸件内部缺陷红外无损检测的有限元模拟及分析[J]. 红外技术, 2008, 30(7): 429-432.

Zhao Jingyuan, Wang Liming, Liu Bin.The Finite Element and Analysis of the Infrared NDT for Inner Defects in Casting Product[J]. Infrared Technology, 2008, 30(7): 429-432.

(编辑张洋)