基于模糊核聚类和引力搜索的风电齿轮箱故障诊断

基于模糊核聚类和引力搜索的风电齿轮箱故障诊断

李状马志勇胡亮柳亦兵

华北电力大学，北京，102206

摘要：为了诊断风电齿轮箱已知类别和未知类别的故障，提出了基于模糊核聚类和引力搜索的故障诊断方法。首先建立以训练样本分类错误率为目标的聚类模型，利用模糊核聚类对训练样本进行分类；然后利用引力搜索算法求解聚类模型，获得最优分类结果下每个类的类心；最后根据新样本与各类心之间的核空间样本相似度判断属于已知故障或者未知故障。结果表明，该方法准确度高，可有效用于风电齿轮箱故障诊断。

关键词：模糊核聚类；引力搜索；风电机组齿轮箱；故障诊断

中图分类号：TH165.3

收稿日期：2015-03-26

基金项目：国家自然科学基金资助项目(51305135)；中央高校基本科研业务费专项资金资助项目(2014XS15)；中国华能集团科技项目(HNKJ13-H20-05)

作者简介：李状，男，1987年生。华北电力大学能源动力与机械工程学院博士研究生。主要研究方向为旋转机械设备故障诊断。发表论文6篇。马志勇，男，1974年生。华北电力大学能源动力与机械工程学院副教授。胡亮，男，1988年生。华北电力大学能源动力与机械工程学院博士研究生。柳亦兵，男，1961年生。华北电力大学能源动力与机械工程学院教授、博士研究生导师。

Fault Diagnosis of Wind Turbine Gearbox Based on Kernel Fuzzy C-means

Clustering and Gravitational Search

Li ZhuangMa ZhiyongHu LiangLiu Yibing

North China Electric Power University,Beijing,102206

Abstract：In order to diagnose known faults and unknown faults of wind turbine gearbox, a method was proposed based on kernel fuzzy c-means clustering and gravitational search. Firstly, the clustering model was built based on wrong classification rate of training samples. The training samples were classified by kernel fuzzy c-means clustering. Then the gravitational search method was introduced for solving the clustering model. The class centers of optimal clustering result were acquired. Finally, the similarity parameters in kernel space between new data samples and the class centers were calculated for diagnosing whether the new data sample belonged to the known faults. The results show that the proposed method has higher precision, which can be applied to diagnose fault of wind turbine gearbox.

Key words：kernel fuzzy c-means clustering; gravitational search; wind turbine gearbox; fault diagnosis

0引言

齿轮箱是风电机组传动链的关键设备，风电机组运行环境恶劣，导致齿轮箱故障频繁发生，不仅事后维修工作难度大，而且费用高。因此对风电机组齿轮箱进行有效的监测和故障诊断具有重要意义。

故障诊断的本质是对故障信息的模式识别与分类[1]。近年来，国内外的许多学者将模式识别方法引入到风电机组故障诊断中。目前，大量的研究多采用基于有监督学习的模式识别方法，例如BP神经网络、支持向量机、故障树分析法[2-6]。这些方法是通过对大量已知故障类别的训练样本的学习，实现待识别样本的分类与诊断。但是这种方法只能识别训练样本中含有的故障类别，当有新类别的样本数据出现时，会给出错误的识别结果，导致错误诊断。实际故障诊断中，获取所有已知故障的大样本数据需要花费大量的人力和时间，难以获取完备的故障样本，这使得基于有监督学习的模式识别方法难以得到有效的应用。

模糊核聚类(kernel fuzzy c-means clustering，KFCM)是一种基于无监督学习的聚类算法，它利用核函数将原始输入空间中的样本数据映射到高维特征空间中再进行模糊聚类，能有效改善复杂数据集的聚类性能[7]，在气动系统、汽轮机、变压器、卫星控制系统[8-11]等故障诊断领域得到了应用。但是在实际工程应用中，KFCM的分类效果依赖初始聚类中心和核函数参数的选择。本文针对上述问题，结合KFCM算法和引力搜索算法(gravitational search algorithm，GSA)[12]，提出一种基于模糊核聚类和引力搜索的风电机组齿轮箱故障诊断方法，实现风电齿轮箱已知和未知类别故障的自动诊断。

1模糊核聚类算法

模糊核聚类算法利用核函数，通过非线性映射将原始特征空间X映射至高维特征空间F后再进行聚类。非线性映射Ф可表示为

Φ∶xk∈X→Φ(xk)∈F

(1)

式中，xk为原始特征空间样本，xk∈X。

KFCM算法的聚类目标函数为

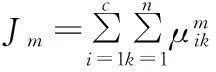
(2)

式中，vi为原始特征空间中第i类的聚类中心，i=1，2，…，c；c为类别数；n为原始特征空间样本数量；μik为第k个样本xk对第i类的隶属度，μik∈[0，1]；m为加权指数。

如果直接将样本映射到高维空间后再进行聚类，则存在确定非线性映射函数的形式和参数、特征空间维数等问题，但采用核函数可以有效地解决该问题。定义核函数K(x，y)=ΦT(x)Φ(y)，这样式(2)中高维空间的欧氏距离可表示为

‖Φ(xk)-Φ(vi)‖2=K(xk,xk)+

K(vi,vi)-2K(xk,vi)

(3)

常见的核函数有高斯核函数、多项式核函数、Sigmoid核函数等，本文选用高斯核函数：

K(x,y)=exp[-‖x-y‖2/(2σ2)]

(4)

式中，σ为高斯核参数。

根据约束条件，结合式(3)、式(4)，运用拉格朗日乘子法求式(2)的极小值，可求得隶属度和聚类中心：

(5)

(6)

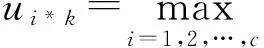
2引力搜索算法

假设在一个d维搜索空间中有N个粒子，定义第l个粒子位置Ql=(ql1，ql2，…，qld)，l=1，2，…，N。

根据牛顿引力定理，在第t次迭代中，第r维上第l个粒子受到第j个粒子的引力为

(7)

G(t)=G0e-αt/T

(8)

式中，ε为一个非常小的常量；MPl(t)为第l个粒子的被动引力质量；MAj(t)为第j个粒子的主动引力质量；G(t)为引力常数；G0=100，α=20；T为最大迭代次数。

所以在第t次迭代，第l个粒子受到来自其他粒子引力合力为

(9)

式中，ωj为区间[0，1]内的一个随机数。

根据牛顿第二定理，粒子Ql在第t次迭代时产生的加速度为

alr(t)=Flr(t)/MIl(t)

(10)

式中，MIl(t)为粒子Ql的惯性质量。

在第t次迭代中，定义粒子Ql的质量为Ml(t)，假设引力质量与惯性质量相等，则有MAl(t)=MPl(t)=MIl(t)=Ml(t)。定义

(11)

(12)

(13)

(14)

式中，fl(t)为在第t次迭代时的适应度值。

在每一次迭代过程中，粒子Ql根据计算得到的加速度来更新粒子的速度和位置，更新公式为

vlr(t+1)=τlvlr(t)+alr(t)

(15)

qlr(t+1)=qlr(t)+vlr(t+1)

(16)

式中，vlr、alr分别为粒子Ql的速度和加速度；τl为区间[0，1]内的一个随机数。

3基于KFCM和GSA故障诊断方法的实现

3.1GSA求解KFCM聚类模型

本文首先利用KFCM法对已知类别的训练样本进行分类。定义一个含有c类、样本特征维数为d的训练样本X，以训练样本的分类错误率评价聚类有效性，并以此为聚类目标建立聚类模型，根据文献[13]，训练样本的分类错误率为

(17)

式中，Ci为数据集X经过KFCM聚类运算后分在第i类的样本集；Ui、|Ui|分别为数据集X中第i类的样本集和所含样本数量；|Ci∩Ui|为Ci和Ui的交集所含元素数量。

利用GSA求解聚类模型，以初始聚类中心和核函数参数为优化变量，定义初始聚类中心Zi=(zi1，zi2，…，zid)，i=1，2，…，c，高斯核参数σ。GSA搜索算法粒子的编码为

Ql=(z11，z12，…，z1d，z21，z22，…，z2d，…，

zc1，zc2，…，zcd，σ)

(18)

以式(17)为目标函数，以聚类中心和高斯核参数为优化变量，搜索W的极小值，则定义适应度函数f=W。GSA求解KFCM聚类模型流程如图1所示。

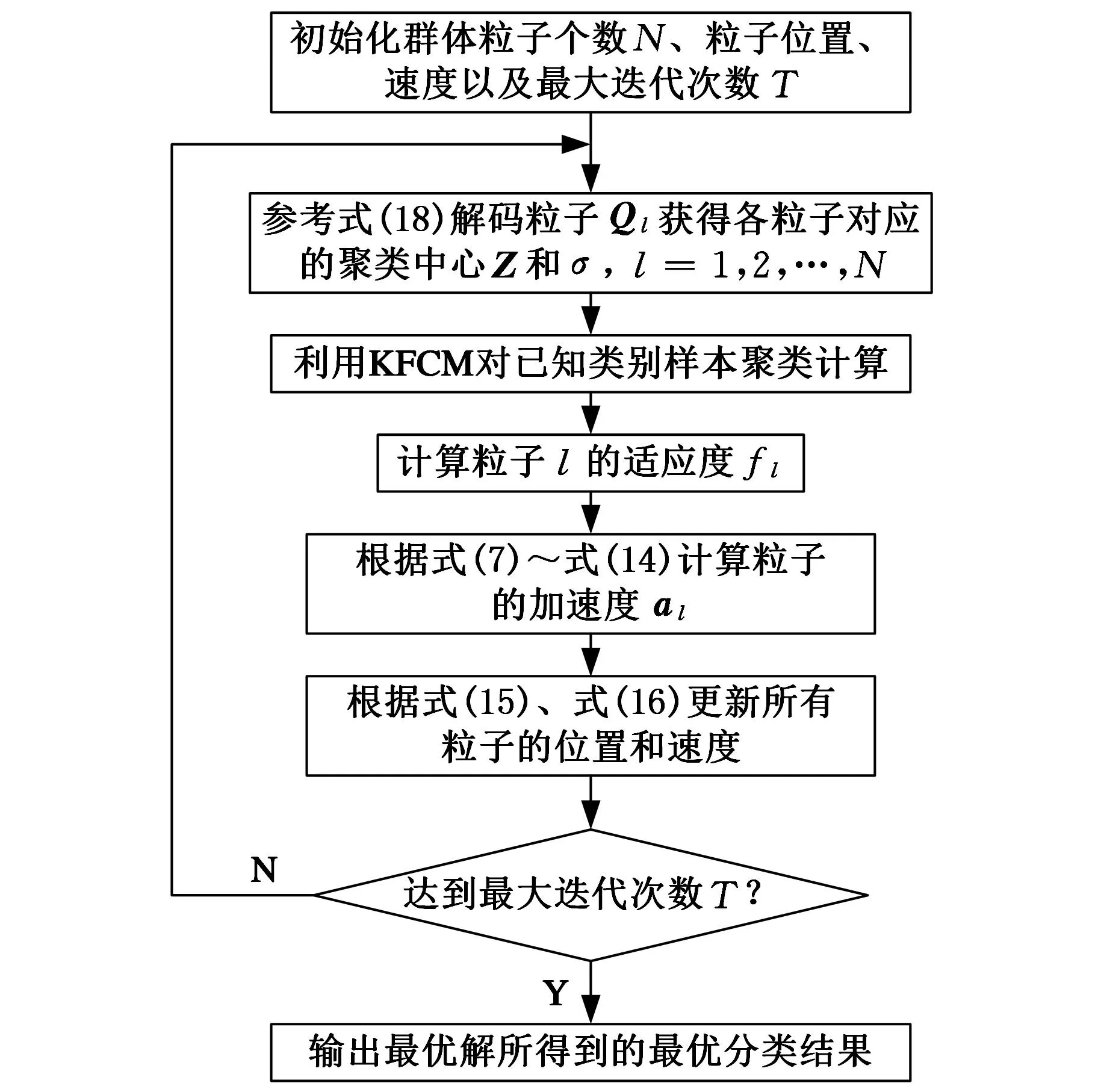
图1　GSA求解KFCM聚类模型流程图

3.2故障诊断流程

基于KFCM和GSA的故障诊断步骤如下：

(1)将已知c类故障的历史数据作为训练样本集X；

(2)利用KFCM对训练样本集进行分类，利用GSA求解KFCM聚类模型，获得最优分类结果的第i类的类心oi；

(3)对于待诊断的新样本xnew，首先根据式(19)计算新样本xnew与类心oi之间的核空间样本相似度[11]：

(19)

davg=∑d(x,oi)/|Ci|，x∈Ci

(20)

式中，d(xnew，oi)为xnew与类心oi在核空间上的欧氏距离；davg为第i类中所有样本与类心oi在核空间上的平均欧式距离；|Ci|为分在第i类的样本数量。

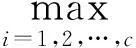
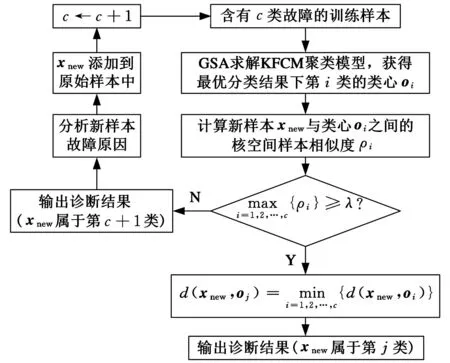
图2　基于KFCM和GSA的故障诊断流程图

4实例分析

4.1风电机组齿轮箱测试描述

以某风电场1.5MW双馈风力发电机组为研究对象，风轮工作转速范围为11～21r/min，齿轮箱采用一级行星轮与两级平行轴结合的传动方案，如图3所示。所选的风电机组齿轮箱在运行过程中曾出现中速级小齿轮裂纹故障(记为F1)、高速级小齿轮点蚀故障(记为F2)和高速输出轴轴承内圈故障(记为F3)。在齿轮箱高速轴轴承座位置安装了压电加速度传感器，采集了风轮工作转速下的正常运行状态(记为N)和3种故障状态的加速度信号，信号采样频率为8192Hz，图4为4种状态下的部分原始时域波形图。

图3　风电机组齿轮箱结构示意图

4.2特征值提取

考虑风电齿轮箱振动信号具有非平稳性，本文选用相对小波包能量作为风电机组齿轮箱振动信号特征值。小波包变换能够对非平稳信号进行有效的分析，相对小波包能量能够反应信号在不同频带内的能量分布，文献[14]给出了相对小波包能量能特征值提取方法，定义如下。

(a)正常

(b)中速级小齿轮裂纹故障

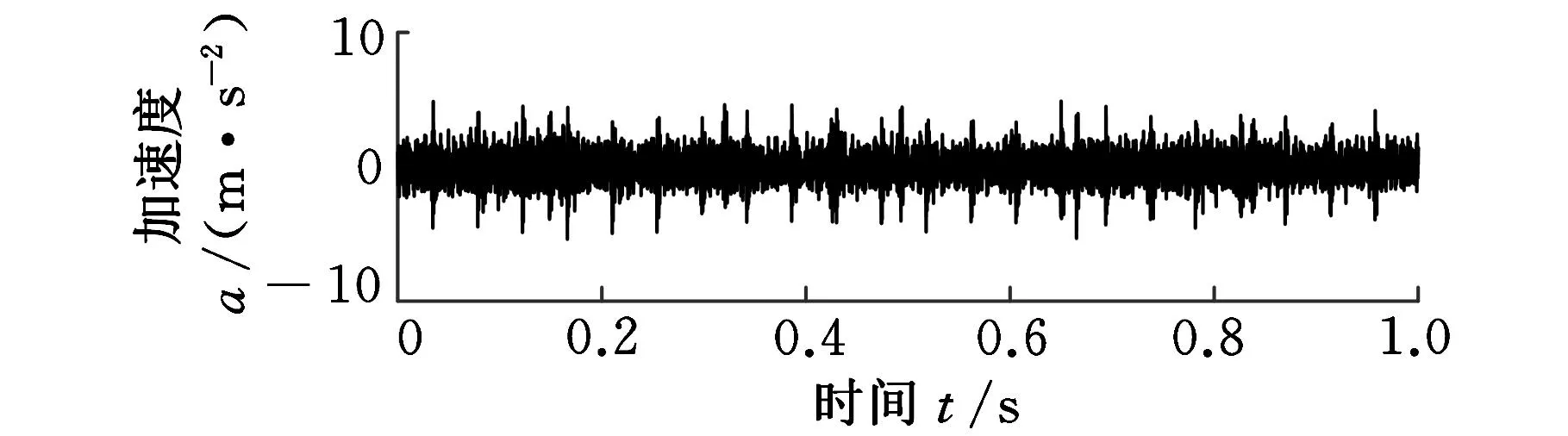
(c)高速级小齿轮点蚀故障

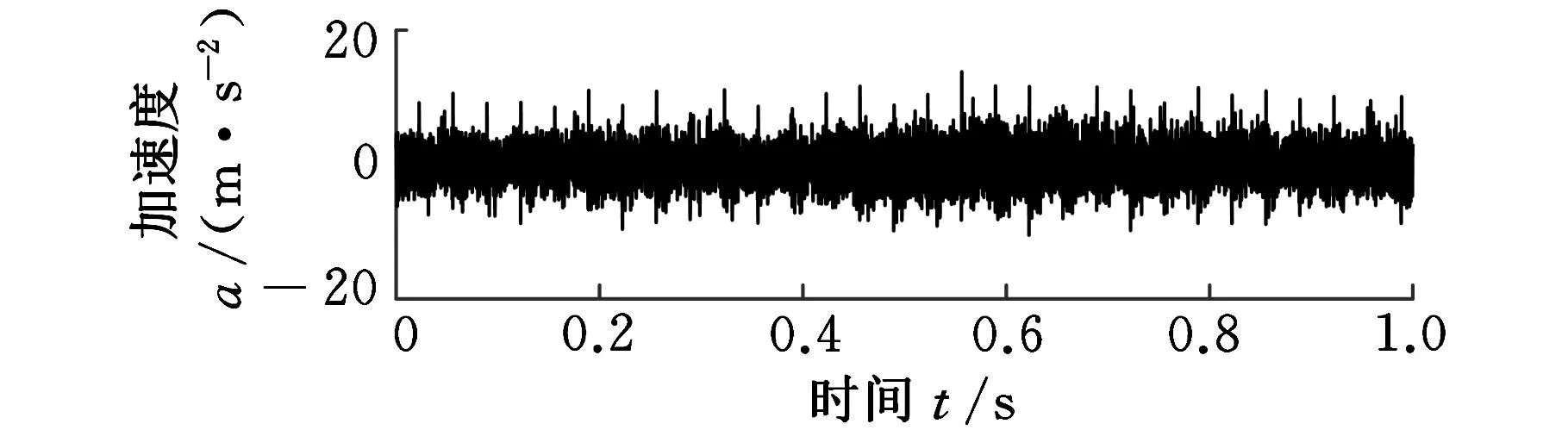
(d)高速输出轴轴承内圈故障 图4　四种状态振动加速度信号时域波形

离散时间信号x(t)经过J层小波包变换后，可以得到2J个频率段的小波包系数CL(k)，L=0，1，…，2J-1，某一频段上的小波包能量定义为该频率段的小波系数的平方和：

(21)

因此，所有频段的总能量为

(22)

相对小波包能量为

εL=EL/E

(23)

为了验证本文提出的方法能够对已知故障进行识别，本文将N、F1和F2作为已知故障，分别编号为1、2、3，并分别从3种状态信号中选取30组样本作为训练样本，总共获得90组训练样本，同时每个状态选取3组样本作为测试样本。为了验证提出的方法能够对未知故障进行判断，将状态F3作为未知故障，并从对应的振动信号中提取3组样本作为测试样本。每个样本采样点数为2048。对每个训练样本和测试样本进行3层小波包变换，根据式(21)～式(23)计算每个频段上的相对小波包能量，并将其作为每个样本信号的特征值，部分训练样本和测试样本数据如表1和表2所示。利用KFCM对训练样本进行分类，运用GSA求解最优分类结果，获得最优分类结果对应的各个类的聚类中心，最终按照图2所示的故障诊断流程对测试样本进行故障分类。

4.3KFCM和GSA参数设置

KFCM和GSA的参数设置如下：类别数量c=3，特征维数d=8，加权指数m=2，群体粒子个数N=50，最大迭代次数T=100，第k个粒子的初始速度vk=0，k=1，2，…，50。运用GSA求解KFCM聚类模型后，得到最优分类结果以及最优分类结果对应的每个类别的聚类中心和核函数参数σ，如表3所示。

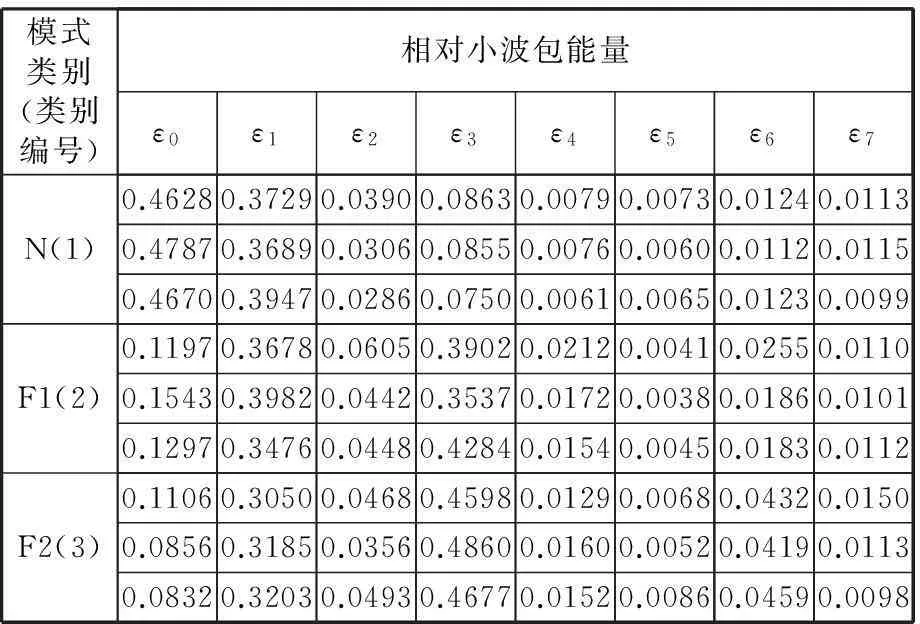
表1　风电齿轮箱部分训练样本特征值

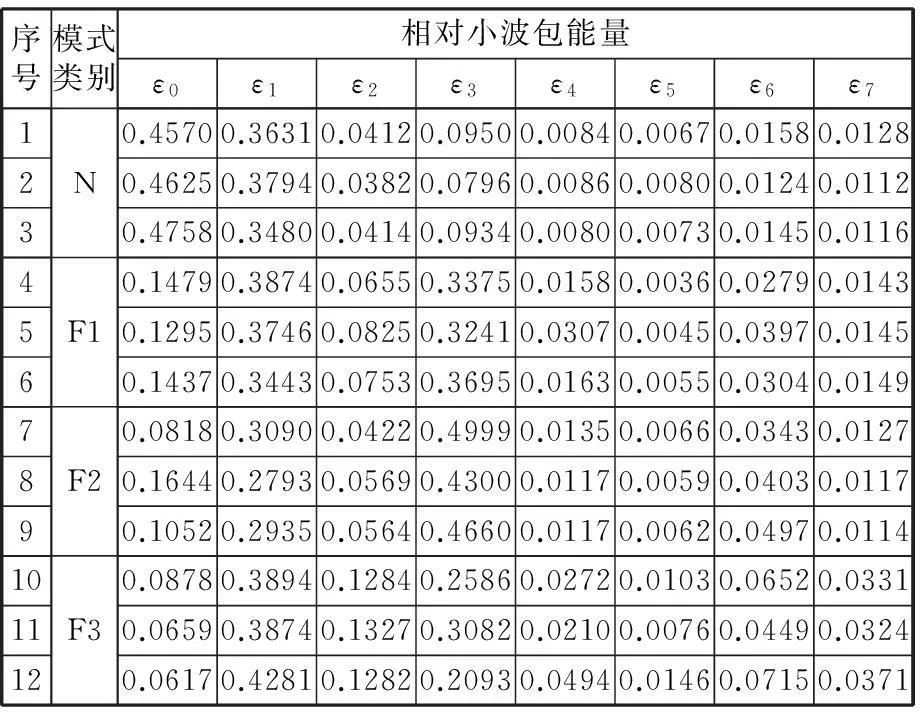
表2　风电齿轮箱测试样本特征值

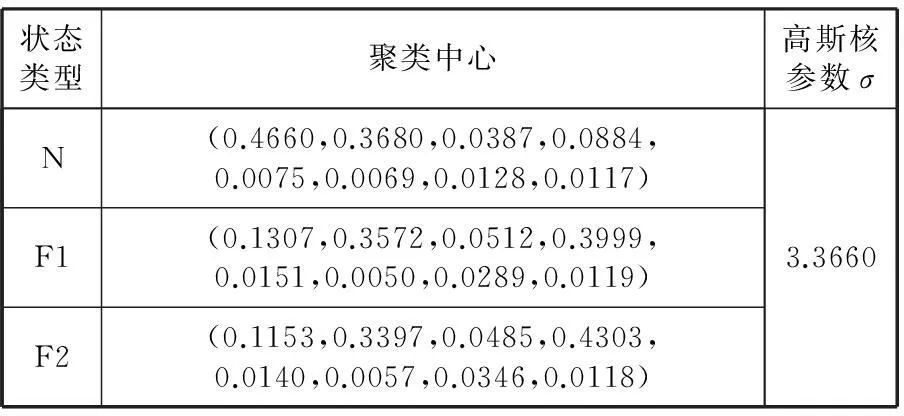
表3　最优分类结果对应的每个类的聚类中心矢量

4.4诊断结果与分析

根据图2所示的诊断流程，对表2中的测试样本进行分类诊断。根据文献[13]给出的λ取值范围，本文选取阈值常数λ=0.2，诊断结果如表4所示。从表4可以看出，前9个样本中，每个样本到各个聚类中心的核空间样本相似度的最大值均大于λ，这表明样本1～9属于已知类别的故障。进一步观察样本1～9与各个聚类中心的核空间欧氏距离可以看出，样本1～3与第1类聚类中心之间的核空间欧氏距离最小，所以样本1～3分为第1类；样本4～6与第2类聚类中心之间的核空间欧氏距离最小，所以样本4～6分为第2类；样本7～9与第3类聚类中心之间的核空间欧氏距离最小，所以样本7～9分在为第3类。样本10～12每个样本到各个聚类中心的核空间样本相似度的最大值均小于λ，表明这3个样本类别不属于训练样本中的已知故障类别，属于未知故障，因此将样本10～12编号为“4”，诊断结果与实际情况相符。

表4　KFCM+GSA诊断结果

最后，本文分别采用BP神经网络和KFCM方法进行故障诊断，诊断结果如表5所示。从表5可以看出，基于有监督学习的BP神经网络可以对已知类别的测试样本1～9给出正确的分类结果，但是对未知类别的测试样本10～12进行分类时，BP神经网络将测试样本分类在已知的故障类别中，与实际结果不符。这是因为BP神经网络只记忆了训练样本中的类别，因此给出了错误的诊断结果。而本文提出的方法将未知类别样本分在第4类，即不属于原有训练样本中的已知故障类别。直接利用KFCM算法由于受到初始聚类中心和核函数参数选取的影响，在对已知类别和未知类别的测试样本分类时均出现了错误分类。与表4的诊断结果进行对比，可以看出本文提出的故障诊断方法更加准确。

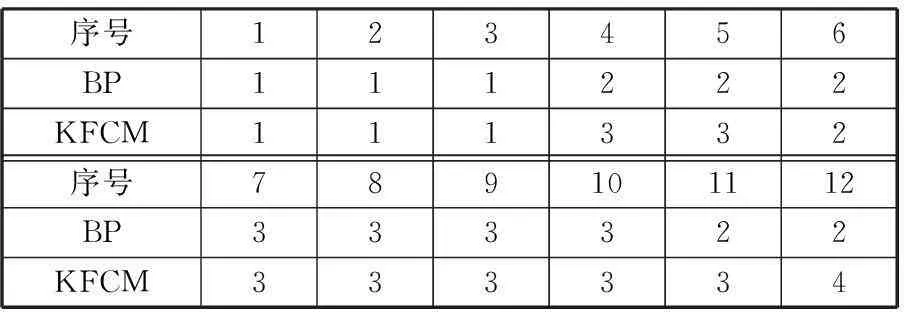
表5　BP神经网络和KFCM诊断结果

5结语

本文提出了一种基于模糊核聚类和引力搜索的风电齿轮箱故障诊断方法，结合实际风电齿轮箱故障样本数据对提出的方法进行了验证，并与传统BP神经网络和KFCM分类方法进行了比较。结果表明，本文提出的方法不仅能够准确地识别诊断出已知类别的故障样本，而且能有效地识别判断出未知类别的故障样本，为风电机组齿轮箱状态监测与故障诊断提供了一种新的思路。

参考文献：

[1]Su Zuqiang，Tang Baoping，Deng Lei，et al. Fault Diagnosis Method Using Supervised Extended Local Tangent Space Alignment for Dimension Reduction[J]. Measurement，2015，62：1-14.

[2]李胜，张培林，李兵，等. 量子BP神经网络在发动机故障诊断中的应用[J]. 中国机械工程，2014，25(16)：2159-2163.

Li Sheng，Zhang Peilin，Li Bing，et al. Applications of Quantum BP Neural Network in Engine Fault Diagnosis[J]. China Mechanical Engineering，2014，25(16)：2159-2163.

[3]龙泉，刘永前，杨勇平. 基于粒子群优化BP神经网络的风电机组齿轮箱故障诊断方法[J]. 太阳能学报，2012，33(1)：120-125.

Long Quang，Liu Yongqian，Yang Yongping. Fault Diagnosis Method of Wind Turbine Gearbox Based on BP Neural Network Trained by Particle Swarm Optimization Algorithm[J]. Acta Energiae Solaris Sinica，2012，33(1)：120-125.

[4]刘丽娟，陈果，郝腾飞. 基于流形学习与一类支持向量机的滚动轴承早期故障识别方法[J]. 中国机械工程，2013，24(5)：628-633.

Liu Lijuan，Chen Guo，Hao Tengfei. Incipient Fault Recognition of Rolling Bearings Based on Manifold Learning and One-class SVM[J]. China Mechanical Engineering，2013，24(5)：628-633.

[5]Tang Baoping，Song Tao，Li Feng，et al. Fault Diagnosis for a Wind Turbine Transmission System Based on Manifold Learning and Shannon Wavelet Support Vector Machine[J]. Renewable Energy，2014，62(3)：1-9.

[6]Yang Zhiling，Wang Bin，Dong Xinghui，et al. Expert System of Fault Diagnosis for Gearbox in Wind Turbine[J]. Systems Engineering Procedia，2012，4：189-195.

[7]Liu Jingwei，Xu Meizhi. Kernelized Fuzzy Attribute C-means Clustering Algorithm[J]. Fuzzy Sets and Systems，2008，159(18)：2428-2445．

[8]蒋全胜，贾民平，胡建中，等. 一种基于人工免疫的模糊核聚类算法[J]. 中国机械工程，2008，19(5)：594-597.

Jiang Quansheng，Jia Minping，Hu Jianzhong，et al. A New Artificial Immunity Based Fuzzy Kernel Clustering Algorithm[J]. China Mechanical Engineering，2008，19(5)：594-597.

[9]黄保海，李岩，王东风，等. 基于KPCA和KFCM集成的汽轮机故障诊断[J]. 电力自动化设备，2010，30(7)：84-87.

Huang Baohai，Li Yan，Wang Dongfeng，et al. Steam Turbine Fault Diagnosis Based on KPCA and KFCM Ensemble[J]. Electric Power Automation Equipment，2010，30(7)：84-87.

[10]Ma Hui，Ekanayake, C，Saha, T K. Power Transformer Fault Diagnosis under Measurement Originated Uncertainties[J]. IEEE Transactions on Dielectrics and Electrical Insulation，2012,19(6)：1982-1990.

[11]Hu Di，Sarosh A，Dong Fengyun. A Novel KFCM Based Fault Diagnosis Method for Unknown Faults in Satellite Reaction Wheels[J]. ISA Transactions，2012，51(2)：309-316.

[12]Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a Gravitational Search Algorithm[J]. Information Sciences，2009，179(13)：2232-2248．

[13]Li Chaoshun, Zhou Jianzhong. Semi-supervised Weighted Kernel Clustering Based on Gravitational Search for Fault Diagnosis[J]. ISA Transactions，2014，53(5)：1534-1543.

[14]Shao Renping，Hu Wentao，Wang Yayun，et al. The Fault Feature Extraction and Classification of Gear Using Principal Component Analysis and Kernel Principal Component Analysis Based on the Wavelet Packet Transform[J]. Measurement，2014，54(6)：118-132.

(编辑张洋)