异步电机混合型滑模磁链观测器分析与验证

异步电机混合型滑模磁链观测器分析与验证

李孟秋周志康廖武彭婧

湖南大学国家电能变换与控制工程技术研究中心，长沙,410082

摘要：在异步电机直接转矩控制中，磁链的观测是精确控制电机的一个重要环节。针对两类无速度传感器滑模观测器，从收敛性和参数敏感性两方面进行了深入的分析，并比较各自的优缺点。结合工程实际需要提出了一种混合型滑模磁链观测器算法。所提出的磁链观测器在控制中能消除初始磁链误差，又具有较好的鲁棒性。MATLAB仿真和实验结果论证了该方法的正确性和有效性。

关键词：直接转矩控制；异步电机；滑模磁链观测器；无传感器

中图分类号：TM343；U469.72

收稿日期：2015-01-06

基金项目：国家国际合作专项(2011DFA62240);国家自然科学基金资助项目(51377050)

作者简介：李孟秋，男，1968年生。湖南大学电气与信息工程学院副教授、博士。主要研究方向为电机电气与电机传动。发表论文10余篇。周志康，男，1989年生。湖南大学电气与信息工程学院硕士研究生。廖武，男，1988年生。湖南大学电气与信息工程学院博士研究生。彭婧，女，1989年生。湖南大学电气与信息工程学院硕士研究生。

Analysis and Verification of Hybrid Sliding Mode Flux Observer of Induction Motors

Li MengqiuZhou ZhikangLiao WuPeng Jing

National Engineering Research Center of Energy Conversion and Control，

Hunan University，Changsha，410082

Abstract:In DTC of induction motors, flux linkage observation is an important part of precise control of motor. The analyses from two aspects of convergence and parameter sensitivity were carried out herein in view of two kinds of speed sensorless sliding mode observer. The advantages and disadvantages of two kinds of speed sensorless sliding mode observer were compared. A hybrid flux observer algorithm combined with the actual needs of engineering was proposed. The initial flux errors might be eliminated in the control of the new hybrid flux observer with good robustness. The correctness and effectiveness of the proposed method were verified by simulations and experiments.

Key words: direct torque control (DTC); induction motor; sliding mode flux observer; sensorless

0引言

准确的定子磁链观测是实现异步电机精确控制的必要条件。异步电机电压模型磁链观测器中，积分偏移和饱和问题使磁链幅值和相位发生偏差。电流模型观测在计算时过于依赖电机时变参数，同时需要速度信息作为输入。对此，学者设计了电压电流混合观测器、自适应全阶观测器、基于扩展卡尔曼滤波观测器等[1-3]，但由于其算法计算量大、对数字处理器要求较高，因而离实际应用都还有一段距离。

滑模控制对系统的模型要求低，对系统自身参数变化和外部扰动有较好的鲁棒性，而成为研究热点[4]。自从Utkin等[5]把滑模理论引入电机控制以来，各国学者对滑模在电机控制中的应用进行了大量的研究[6-7]。Tursini等[8]把自适应理论与滑模观测器相结合，得到能同时估算磁链和速度的观测器。Zhao等[9]把滑模观测器和参数辨识相结合，对转子时间常数和定子电阻进行辨识。

本文对两类不同的滑模观测器(利用滑模控制函数对电压分量进行整体补偿的观测器、利用滑模控制函数对误差电压进行补偿的观测器)，依据Lyapunov稳定性理论进行分析与对比，得出两类观测器的优缺点。为改善其性能以满足实际需要，进一步提出基于两者的混合型滑模磁链观测器(在同一系统中，按一定条件实时切换两种观测器)。

1异步电机数学模型

在静止坐标系下，异步电机的状态方程为

(1)

式中，Ls、Lr分别为电机的定转子电感；Lm为励磁电感；Rs、Rr分别为电机的定转子电阻；σ为电机漏磁系数；Tr为转子时间常数；J、np分别为电机的转动惯量和极对数；ω为电机机械角速度；ψrα、ψrβ为α、β轴的转子磁通；isα、isβ分别为α、β轴的定子电流；usα、usβ分别为α、β轴定子电压。

可见，异步电机是一个非线性的高阶系统。在异步电机的数学模型中，电流的状态方程和转子磁链的状态方程中有共同的多项式-Aψ-Bψ+k1i。

2滑模观测器的分析与改进

2.1基于滑模等效控制函数补偿整体电压的观测器

在实际应用中，磁链由于不可测而作为观测量，电机电压电流的测量非常方便，所以一般以定子电流为输出变量，电压为输入变量，速度为系统矩阵的参数列出方程构造磁链观测器。文献[10-12]提出来的三种滑模观测器分别为

(2)

(3)

(4)

式中，k为滑模增益常数；符号^代表估算值。

在基于滑模等效控制函数补偿整体电压的观测器(式(2)～式(4))的共同特征是，先利用滑模电流观测器的控制函数等效磁链方程中的Aψ+Bψ-k1i、Aψ+Bψ或Bψ，即电压或反电动势Ueq，再由磁链观测器利用此电压或反电动势，观测出磁链。由于速度信息包含在滑模等效反电动势中，所以这3种观测器计算方法都不需要知道电机的速度信息。

Ueq的等效分量含有共同项Bψ，由于B为速度矩阵，所以上述的3种观测器算法都不需要电机的速度信息，就可以计算出磁链的大小。根据等效的结果可以很容易分离出电机的速度信息，即得到速度的估算值。

下面对这种类型的滑模观测器进行分析，在不考虑电机参数变化的情况下把式(1)减去式(2)可得

(5)

定义电流观测器的Lyapunov函数为

(6)

很容易可以看出电流观测器的Lyapunov函数是恒非负的。对V1求导可得

(7)

把式(5)代入式(7)可得

(hk1+k2)(iαΔiα+iβΔiβ)-k(uαΔiα+uβΔiβ)

(8)

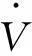
kU=Ueq=h(A+B)ψ-hk1i

(9)

即滑模控制函数的输出等效为h(A+B)ψ-hk1i。值得注意的是，不管电机的参数怎么变动，这种收敛性会一直存在，即电流估算值一定会收敛于实际值。

下面分析磁链的收敛性。定义磁链观测器的Lyapunov函数为

(10)

所以其导数为

(11)

下面考虑电机定子电阻和转子电阻参数变化的影响，对滑模观测器的参数鲁棒性进行分析。假设电机的定转子电阻发生变化，分别增加ΔRs和ΔRr，对式(4)对应滑模观测器进行分析，仿照前面的方法可以知

Ueq=hAΔψ+hΔAψ+hBψ-

(hk1ΔRr/Rr+k2ΔRs/Rs)i

(12)

将式(12)代入磁链观测器可得到磁链估算值：

(13)

该观测器算法只对定子电阻的变化敏感，转子电阻的变化对其观测正确性没有影响。式(3)、式(4)对应的观测器也可得出相同的结论。

2.2基于滑模等效控制函数补偿误差电压观测器

基于滑模等效控制函数补偿误差电压观测器算法，利用等效滑模控制函数补偿电机参数变化引起的电压或反电势误差。此滑模观测器计算方程为

(14)

式(14)对应的滑模观测器结构如图1所示。

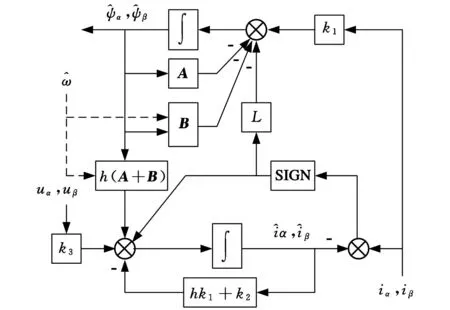
图1　补偿误差电压型滑模观测器结构框图

与整体补偿(图2)相比，此观测器算法需要速度的信息作为输入，算法结构形式比整体补偿算法的复杂，但反馈增益矩阵的选择有较高的灵活性，可以通过选取不同的反馈矩阵，设计出对任意初值可以收敛的磁链观测器。此观测器算法由于滑模控制函数只对电压误差进行补偿处理，所以从等效控制函数中分离出速度信息变得非常困难。滑模观测器的速度信息可以利用电机模型直接计算得到，或参考自适应的方法得到，即以电机实际模型为参考模型，观测器作为可调模型，自适应得出电机的速度[13]。下面对式(14)给出的观测器算法进行分析。在不考虑电机参数变化的情况下把式(1)减去式(14)，可得

(15)

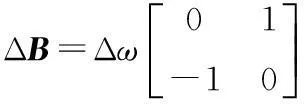
图2　补偿整体电压型滑模观测器结构框图

仿照式(8)可以得出“只要k足够大，电流观测器就能收敛”的结论。当电流观测器收敛时，可得

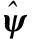
(16)

从式(16)可以看出，滑模控制函数只对电机参数变化引起的电压误差进行补偿。把式(16)代入式(15)中的磁链观测器，可得

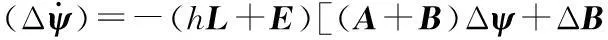
(17)

式中，E为单位矩阵。

仿照式(10)定义磁链观测器的Lyapunov函数，并把式(15)代入式(17)可得

h[(l4-l1)ω-(l2+l3)/Tr]ΔψαΔψβ+

[(1-hl1)/Tr+hl2ω](Δψα)2+

[(1-hl4)/Tr-hl3ω](Δψβ)2

(18)

(hk1ΔRr/Rr+k2ΔRs/Rs)i

(19)

把Ueq与反馈增益矩阵L相乘后，代入磁链观测器，得

(20)

由此可见，该磁链观测器的参数敏感性不仅和定子电阻的变化有关，还会受到反馈增益矩阵以及Ueq的影响，并且这种影响是在α、β轴之间相互耦合的。这导致定子和转子电阻的变化都会对磁链观测的精度产生影响。以上只考虑了电机速度误差为零的情况，当考虑电机速度误差时，电机速度输入不准确只会影响磁链幅值的正确性，对磁链角度不会有任何影响。

2.3混合滑模磁链观测器

结合工程实践提出了可平滑切换的两种磁链观测器的控制策略：以初始速度为起始磁链观测器的选择依据；以磁链幅值收敛为运行中磁链观测器的切换依据。当初始速度为零即从零开始启动(isα=iβ=0即电机实际输入电流为零时，判断此时速度为零)时，选用第一类观测器。此时磁链观测器无需进行切换控制，第一类观测器作用于电机运行全过程。当速度不为零时，启动时选用第二种磁链观测器，实时的判断条件为

(21)

式中，ψi(t)、ψi(t+1)分别为第i(i=1，2)类观测器t时刻、t+1时刻的磁链幅值；t为一个采样周期。

式(21)成立，表明磁链收敛，可进行磁链的平滑切换，即切换到第一类磁链观测器。此时保存切换前一时刻的ψ2(t)，即稳定的磁链幅值。由上文分析可知，第二类磁链观测器对初始磁链误差具有较好的收敛性，即ψ2(t)为此时准确的磁链幅值。在下一时刻，将记录的ψ2(t)作为切换后第一类磁链观测器的初值ψ1(t+1)。

采用的混合滑模磁链观测器算法综合考虑到上述两种磁链观测器的特点，以任何方式启动电机，磁链都能稳定收敛且无初始误差，对电机因长时间运行导致的电阻参数变化具有较好的鲁棒性。滑模磁链观测器快速平滑过渡切换控制流程图如图3所示。

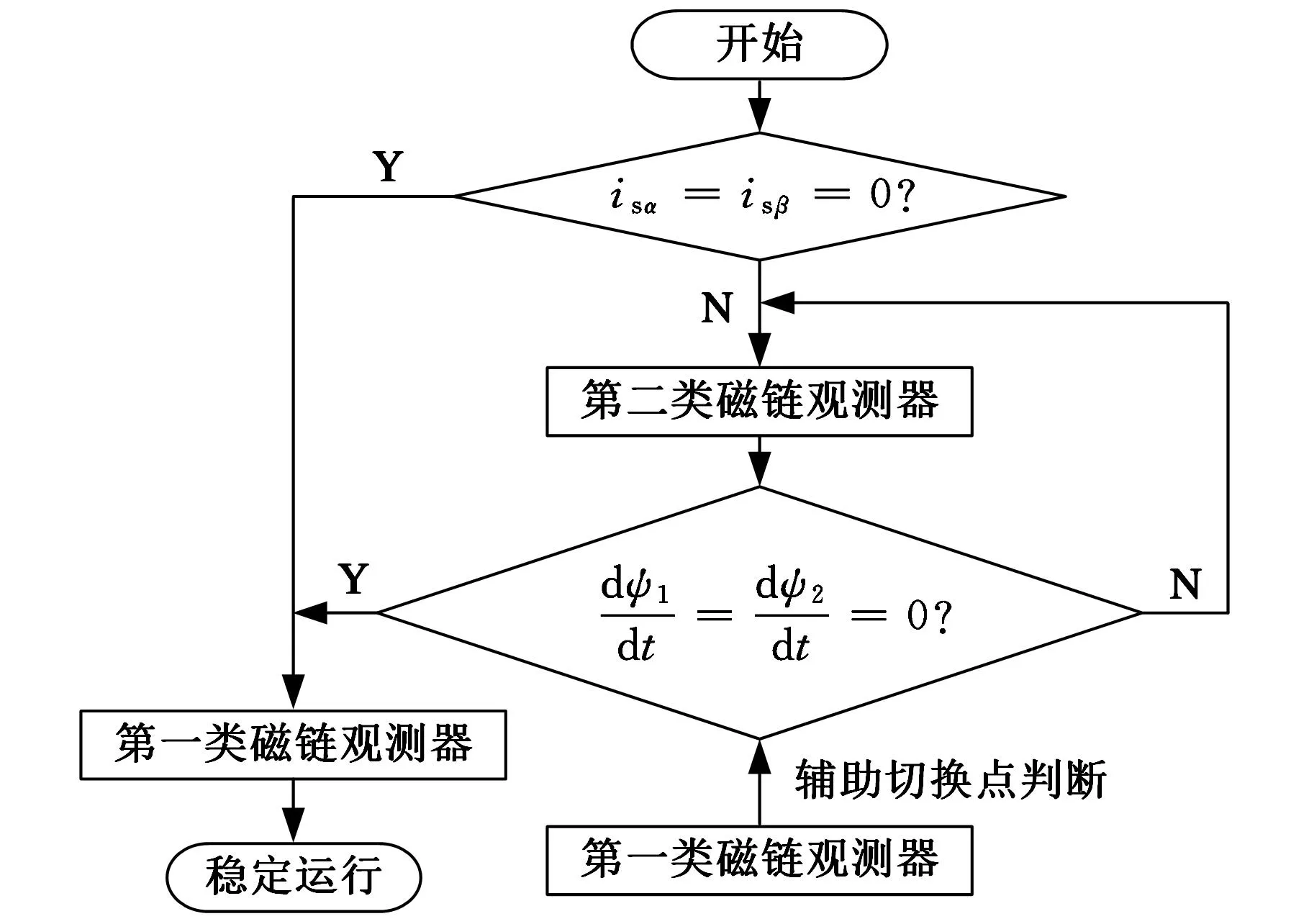
图3　切换控制流程图

3仿真和试验验证

3.1仿真研究

电机仿真参数设置为：额定线电压400V，额定频率50Hz，额定功率4kW，定子电阻1.405Ω，定子漏感5.839mH，转子电阻1.395Ω，转子漏感5.839mH，励磁电感172.2mH，转动惯量0.0131kg·m2，极对数为2。这里滑模增益常数取16 000，所有状态变量的初始状态全为零。第二种观测器的反馈矩阵各元素值取为l1=l4=1/h，l2=-l3=-1，图4是在0～0.4s内电机从静止开始加速的动态曲线，在0.2s时突加20N·m负载。

图4　电机的速度及磁链曲线

观测器稳定性的分析。当观测器的初值都设为0或与实际磁链一致时，磁链观测器能够很好地估算出实际磁链。下面分析起始定子磁链初值不正确时，两种磁链观测器计算磁链的收敛情况。两种观测器的磁链的初值都设为0.2Wb，仿真结果如图5所示。从图5a可以看出，第一种磁链观测值始终存在0.2Wb的初始误差，不能随时间的增加把误差调为0；图5b中，第二种观测器的误差能够在短时间迅速收敛，从而证实了该磁链观测器收敛性的正确性。

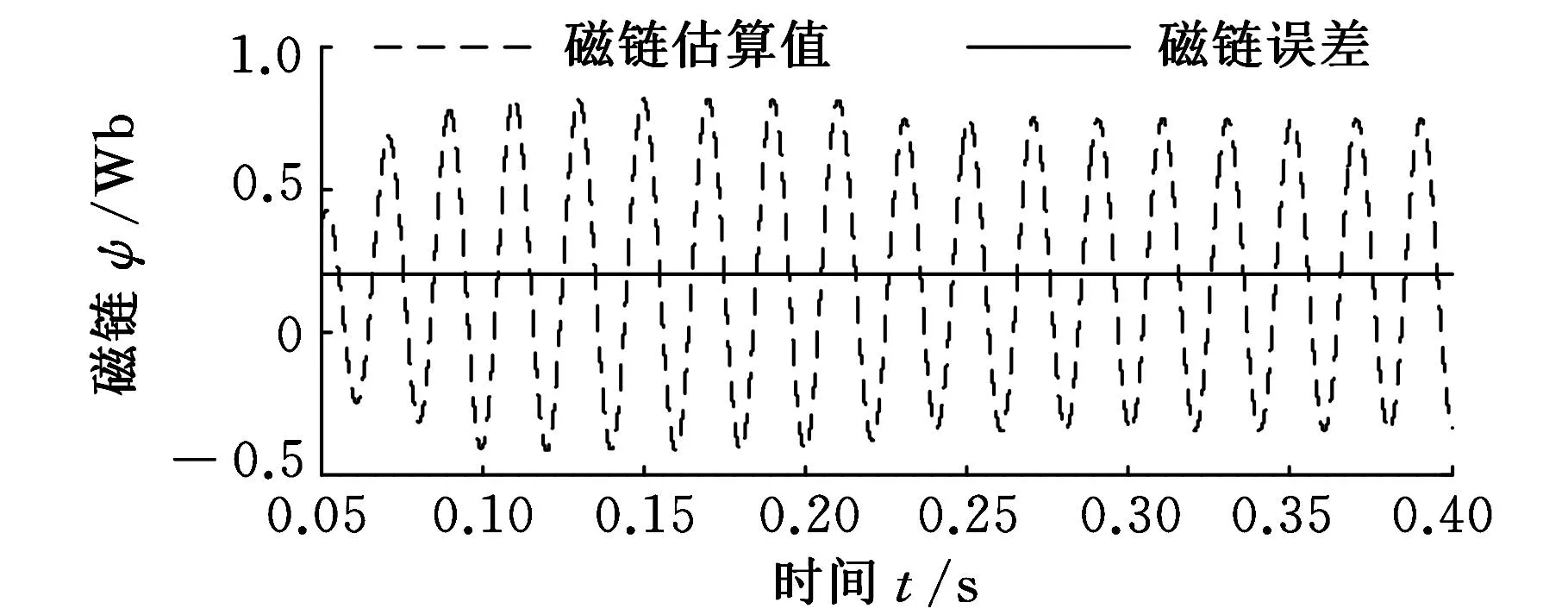
(a)第一种磁链观测器磁链波形

(b)第二种磁链观测器的磁链波形 图5　初值不正确时α轴磁链的估算值与误差值

对于参数的敏感性分析，电压仍按上述工况运行，第一种和第二种观测器的转子电阻取值在0.3s时突增50%，仿真结果如图6所示。从图6a可以看出，0.3s时，第一种观测器的估算值和实际值几乎一致，可见转子电阻的变化对观测器几乎没有影响。第二种观测器在0.3s时要受到转子电阻误差的影响，如图6b所示。

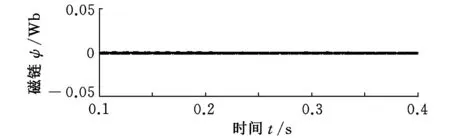
(a)第一种磁链观测器磁链误差

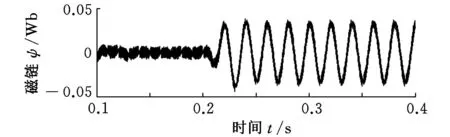
(b)第二种磁链观测器磁链误差 图6　转子电阻增加50%时磁链的估算值与实际值的差

对混合型滑模磁链观测器进行仿真，考虑实际应用情况，选择变频变压调速启动，在0.05s系统选择混合滑模磁链观测器算法进行电机控制，从图7可以看出，0.05s时的磁链初值约为0.2Wb，在仿真中人为地将转子电阻在0.2s时突增50%，图7中未出现较大的磁链误差。由此，混合型磁链观测器的收敛性和鲁棒性得到了验证。

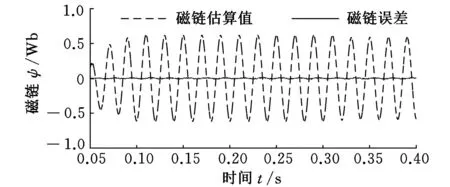
图7　混合型观测器轴α磁链估算值与误差值

3.2实验验证

实验在一台4kW异步电机机组上完成，其他电机参数与仿真参数相同。实验通过对轴连接的电机发电运行来对实验电机加载。

本系统选用TMS320F28335作为控制芯片。为避免其他因素的影响，较好分析混合滑模磁链观测器的性能，试验采用光电编码器直接获取速度，未引入无速度传感器算法。由于实验条件有限，磁链波形无法直接测量，所以借助CCS软件，通过DA转换，经示波器进行观测。系统结构如图8所示。

图8　系统结构图

电机控制采用混合滑模磁链模型，通过定转子磁链计算方程得出定子磁链，并与含速度反馈信号电流型磁链观测器作比较[14]。电机在800r/min稳定运行，混合磁链观测器的幅值与给定的定子磁链幅值0.7Wb接近，差值很小。因此，稳定运行时，混合磁链观测器能够较精确地估算定子磁链幅值。定子磁链幅值在运行过程中并没有产生误差，验证了混合型滑模磁链观测器的正确性和可行性。当两类磁链观测器计算的定子磁链幅值满足式(21)时，计算的磁链幅值稳定，可作为两磁链观测器间的切换条件。

4结语

本文比较了2种异步电机无速度传感器滑模磁链估算方法。第一种观测器具有实现简单、鲁棒性好的优点，不会因电机转子电阻的变化对磁链观测结果产生影响，但对于任意的磁链初值，不能消除初始误差。第二种观测器通过适当的配置反馈矩阵，来消除初始误差，但磁链的观测值会受到定子和转子电阻的影响，参数敏感性不如前者。综合考虑两者的优缺点，提出按照实际情况对上述两类滑模磁链观测器进行实时切换，将构成的混合滑模磁链观测器应用到一个控制系统中。仿真和实验结果表明，混合滑模磁链观测器既能消除初始磁链误差，又具有较好的鲁棒性。

参考文献：

[1]张杰，柴建云，孙旭东，等. 基于反电动势与磁链正交性的异步电机电压模型积分改进算法[J]. 电工技术学报，2014，29(3): 41-49.

ZhangJie,ChaiJianyun,SunXudong,etal.AnImprovedVoltageModelIntegralAlgorithmofInductionMotorsBasedontheOrthogonalitybetweenBackEMFandFlux[J].TransactionsofChinaElectrotechnicalSocity, 2014, 29(3): 41-49.

[2]宋文祥，周杰，朱洪志，等. 基于自适应的全阶观测器的感应电机低速发电运行稳定性[J]. 电工技术学报，2014，29(3): 196-205.

SongWenxiang，ZhouJie，ZhuHongzhi，etal.Regenerating-modeStabilizationofInductionMotorBasedonAdaptiveFull-orderObserver[J].TransactionsofChinaElectrotechnicalSocity, 2014, 29(3): 196-205.

[3]尹忠刚，赵昌，重彦儒，等. 采用抗差扩展卡尔曼滤波器的感应电机转速估计方法[J]. 中国电机工程学报，2012，32(18)：152-159.

YinZhonggang,ZhaoChang,ZhongYanru,etal.ASpeedEstimationMethodofInductionMotorUsingtheRobustExtendedKalmanFilter[J].ProceedingsoftheCSEE, 2012, 32(18): 152-159.

[4]刘春芳, 张健. 数控机床用磁悬浮系统非线性时变滑模变结构控制[J]. 中国机械工程, 2013, 24(21): 2921-2927.

LiuChunfang,ZhangJian.NonlinearTime-varyingSlidingModeControlforNCMachineMagneticLevitationSystems[J].ChinaMechanicalEngineering, 2013, 24(21): 2921-2927.

[5]UtkinV,GuldnerJ,ShiJ.SlidingModeControlinElectro-mechanicalSystems[M].BocaRaton,FL,USA：CRCPress, 2009.

[6]廖永衡，冯晓云，王珍，基于定子磁链滑模观测器的异步电机空间矢量调制直接转矩控制[J]. 中国电机工程学报，2012，32(18)：88-97.

LiaoYongheng,FengXiaoyun,WangZhen.InductionMotorDirectTorqueControlBasedonStatorFluxSlidingModeObserverandSpaceVectorPulseWidthModulation[J].ProceedingsoftheCSEE, 2012, 32(28): 88-97.

[7]史宏宇，冯勇. 感应电机高阶终端滑模观测器的研究[J]. 自动化学报, 2012, 38(2): 288-293.

ShiHongyu,FengYong.High-orderTerminalSlidingModeFluxObserverforInductionMotors[J].ActaAutomaticaSinica, 2012, 38(2): 288-293.

[8]TursiniM,PetrellaR,ParasilitiF.AdaptiveSliding-modeObserverforSpeed-sensorlessControlofInductionMotors[J].IEEETransactionsonIndustryApplications, 2000, 36(5): 1380-1387.

[9]ZhaoL,HuangJ,LiuH,etal.Second-orderSliding-modeObserverwithOnlineParameterIdentificationforSensorlessInductionMotorDrives[J].IEEETransactionsonIndustrialElectronics, 2014, 61(10): 5280-5289.

[10]RehmanH,DerdiyokA,GuvenMK,etal.ANewCurrentModelFluxObserverforWideSpeedRangeSensorlessControlofanInductionMachine[J].IEEETransactionsonPowerElectronics, 2002, 17(6): 1041-1048.

[11]DerdiyokA,RehmanH,GüvenMK,etal.ARobustSlidingModeObserverforSpeedEstimationofInductionMachine[C]//AppliedPowerElectronicsConferenceandExposition.Columbus,USA,2001: 413-418.

[12]LascuC,BoldeaI,BlaabjergF.AClassofSpeed-sensorlessSliding-modeObserversforHigh-performanceInductionMotorDrives[J].IEEETransactionsonIndustrialElectronics, 2009, 56(9): 3394-3403.

[13]RindS,RenY,JiangL.MRASBasedSpeedSensorlessIndirectVectorControlofInductionMotorDriveforElectricVehicles[C]//PowerEngineeringConference(UPEC).Liverpool,UK, 2014: 1-6.

[14]周扬忠，毛洁. 基于有效磁链概念的永磁同步电机新型定子磁链滑模观测器[J]. 中国电机工程学报，2013，33(12)：152-158.

ZhouYangzhong,MaoJie.ANovelSlidingModeStatorFluxLinkageEstimatorBasedonActiveFluxPrincipleforPermanentMagnetSynchronousMotors[J].ProceedingsoftheCSEE, 2013, 33(12): 152-158.

(编辑张洋)