基于ASTFA的广义解调方法及应用

基于ASTFA的广义解调方法及应用

李宝庆程军圣彭延峰杨宇

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

摘要：结合自适应最稀疏时频分析(ASTFA)和广义解调的优点提出了基于ASTFA的广义解调方法。该方法首先采用ASTFA对原始信号进行分解，得到分量信号及其相位函数；然后，提取该相位函数的二次项及高次项，获得解调相位函数；之后利用解调相位函数对分量信号进行广义解调；最后对广义解调后的信号进行频域分析，提取特征信息。仿真和实验分析结果表明，基于ASTFA的广义解调方法非常适用于处理多分量频率调制信号，能够有效提取滚动轴承在变速工况下的故障特征信息。

关键词：自适应最稀疏时频分析；广义解调；相位函数；频率调制；滚动轴承

中图分类号：TH113.1；TH911.7

收稿日期：2015-03-23

基金项目：国家自然科学基金资助项目(51375152)

作者简介：李宝庆，男，1984年生。湖南大学机械与运载工程学院博士研究生。主要研究方向为机械设备故障诊断、动态信号分析与处理。发表论文2篇。程军圣，男，1968年生。湖南大学机械与运载工程学院教授、博士研究生导师。彭延峰，男，1988年生。湖南大学机械与运载工程学院博士研究生。杨宇，女，1971年生。湖南大学机械与运载工程学院教授、博士研究生导师。

Generalized Demodulation Method Based on ASTFA Method and Its Applications

Li BaoqingCheng JunshengPeng YanfengYang Yu

State key Laboratory of Advanced Design and Manufacture for Vehicle Body,

Hunan University, Changsha, 410082

Abstract:Combining with the advantages of the ASTFA and the generalized demodulation, a generalized demodulation method was proposed based on the ASTFA. Firstly, the original signals were decomposed via ASTFA,and the component and its corresponding phase function were obtained. Secondly, the demodulation phase function was formatted by extracting the secondary and higher order terms of the phase function. Then, the generalized demodulation method was applied to the component using the demodulation phase demodulation function. Finally, the frequency domain analyses were applied to the demodulated component to extract feature information. Simulation and experimental analyses show that the method is very suitable for processing multi-component frequency modulated signals, and can effectively extract the damage characteristic informations of the rolling bearing damages in shifting conditions.

Key words: adaptive and sparsest time-frequency analysis(ASTFA); generalized demodulation; phase function; frequency modulation; rolling bearing

0引言

当滚动轴承出现故障时，会产生以轴承元件固有频率为载波频率的多频率调制信号(表现为不断重复的脉冲衰减信号)。对信号进行频域分析，获取脉冲出现的频率成为轴承损伤判别的关键[1]。滚动轴承在升降速过程中的振动信号包含了丰富的状态信息，一些在平稳运行时不易反映的特征信息可能会被充分地表现出来，对升降速过程中的振动信号进行分析具有重要意义。转速变化时，轴承的特征信息表现为频率曲线变化的非平稳信号，傅里叶变换等传统的故障诊断方法不再适用[2]。工程上一般采用阶次分析方法来实现非平稳信号的平稳化，它可以将变速过程中产生的与转速有关的振动信号有效地分离出来[3]。但是，阶次分析方法首先需要获取转速信号，采用传感器等硬件获取转速需要较高的成本，而且在一些场合无法通过硬件获取转速[4]。有学者基于原始振动信号的瞬时频率估计来提取转速信号[4-5]，但是通过这种方式得到的转速信号准确度欠佳。另外，阶次分析中的角域重采样阶次不容易确定。文献[6]提出了一种滤波定阶方法，但在选择滤波器截止频率时存在一定的主观性。Olhede等[7]提出的广义解调方法同样能够实现非平稳信号的平稳化，它把时频分布是倾斜、非线性或曲线的非平稳信号变换为时频分布是线性和平行于时间坐标轴的平稳信号。广义解调方法的关键是解调相位函数的选择[8-9]。目前都是基于先验知识来估计解调相位函数，文献[9-10]先采用最大离散小波包变换获得原始信号的近似时频分布，再估计解调相位函数。文献[11]利用基于多尺度线调频基的稀疏信号分解(multi-scale chirplet path pursuit，MCPP)方法先将频率曲线变化的多分量信号分解为单分量信号，获得各分量的瞬时频率曲线，然后对各分量的瞬时频率进行积分估计解调相位函数。无论是基于近似时频分布，还是基于瞬时频率的积分来估计解调相位函数都存在误差，严重时会造成错误的广义解调结果。

近期， Hou等[12-13]提出了一种自适应最稀疏时频分析(adaptive and sparsest time-frequency analysis，ASTFA)方法。该方法在信号分解的同时可以直接获得各分量的相位函数，无需先验知识。提取该相位函数的二次项及高次项就可以获得解调相位函数，利用该解调相位函数对分量信号进行广义解调后，分量信号的时频分布为平行于时间坐标轴的直线，实现了非平稳信号的平稳化。利用ASTFA方法获得的解调相位函数具有更好的准确度。

本文结合ASTFA和广义解调的优点，提出了基于ASTFA的广义解调方法。首先使用ASTFA对原始信号进行分解，得到分量信号并获得相位函数，然后提取该相位函数的二次项及高次项作为解调相位函数用于广义解调，最后对广义解调后的信号进行频域分析提取特征信息。本文利用该方法对变速工况下存在故障的滚动轴承振动信号进行了分析，实际应用表明该方法能够有效提取相应的特征信息。

1基于ASTFA的广义解调方法

1.1广义解调

广义解调方法能把时频分布是倾斜、非线性或曲线的非平稳信号变换为时频分布是线性和平行于时间轴的平稳信号，本质上是广义傅里叶变换(generalized Fourier transform，GFT)。信号x(t)的GFT定义为

(1)

其中，s0(t)为随时间变化的实值函数。GFT实际上是对x(t)exp(-j2πs0(t))作标准傅里叶变换。设信号x(t)=exp(-j2π(f0t+s0(t)))，如果找到近似s0(t)的相位函数s(t)，对信号x(t)进行GFT：

exp(-j2π(ft+s(t)))dt=

(2)

1.2ASTFA方法

多尺度信号在时频分布上具有稀疏分布的特点，基于此，ASTFA在建立包含所有自适应基的过完备字典库的基础上寻找信号的最稀疏表达。ASTFA首先建立合适的包含所有自适应基的过完备字典库，然后在过完备字典库中搜索对信号的匹配性最好的自适应基。

(1)过完备字典库：

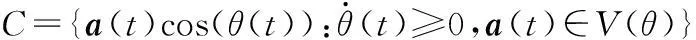
(3)

k=0,1,…,λn；l=1,2,…,λn}

(4)

(2)最优化问题:

(5)

上述优化问题是一个L0优化问题，即NP-Hard问题。根据逼近论，采用对L0范数不同的逼近方式可以将上述问题转化为其他的优化问题，如L1或L2优化问题[14]。ASTFA方法将上述L0优化问题转化为L2优化问题，并采用高斯牛顿迭代方法解决该问题。主要的计算步骤如下。

(1)令初始残差r0=f(t)；

(2)求解非线性最小二乘问题：

(6)

式中，ui(t)为分解得到的第i个内禀模态函数分量；ai(t)为分量的瞬时幅值；θi(t)为分量的相位函数。

(3)更新残差：

ri=ri-1-ai(t)cosθi(t)

(7)

1.3广义解调相位函数的选择

为区分广义解调的相位函数与ASTFA方法中的相位函数，本文将广义解调的相位函数称为解调相位函数，用s(t)表示；将ASTFA方法中的相位函数称为相位函数，用θ(t)表示。

(8)

那么

(9)

式(9)表明解调相位函数s(t)为时间t的二次项及高次项之和。

按ASTFA方法原理及式(9)可得相位函数θ(t)与解调相位函数s(t)之间的关系：

s(t)=Θ(t)/(2π)

(10)

其中，Θ(t)为相位函数θ(t)的二次项及高次项之和。提取ASTFA获得的相位函数θ(t)的二次项及高次项，再除以系数2π就可以获得广义解调的解调相位函数s(t)，无需获得原始信号的先验时频分布。

1.4基于ASTFA的广义解调方法

基于ASTFA的广义解调方法步骤如下：

(1)采用ASTFA方法对原始信号进行分析，同时获得分量信号及其相位函数θi(t)。

(2)采用式(9)对相位函数θi(t)进行处理，获得解调相位函数si(t)。

(3)使用解调相位函数si(t)对各分量信号进行广义解调。

(4)对广义解调后的信号进行频域分析，可采用FFT变换产生幅值谱。

2仿真信号分析

为验证基于自适应最稀疏时频分析的广义解调方法对多分量调频信号分析的有效性，考察两个幅值不等的调频信号组成的仿真信号:

x(t)=x1(t)+x2(t)

(11)

x1(t)=3cos(120t3-80t2+500t)

x2(t)=cos(120t3-80t2+800t)

其中，t∈[0,1]，单位：s。

仿真信号的时域波形如图1所示，分解结果如图2所示。从图2可以看出，两个调频信号已经完全分离。

图1　仿真信号x(t)的时域波形

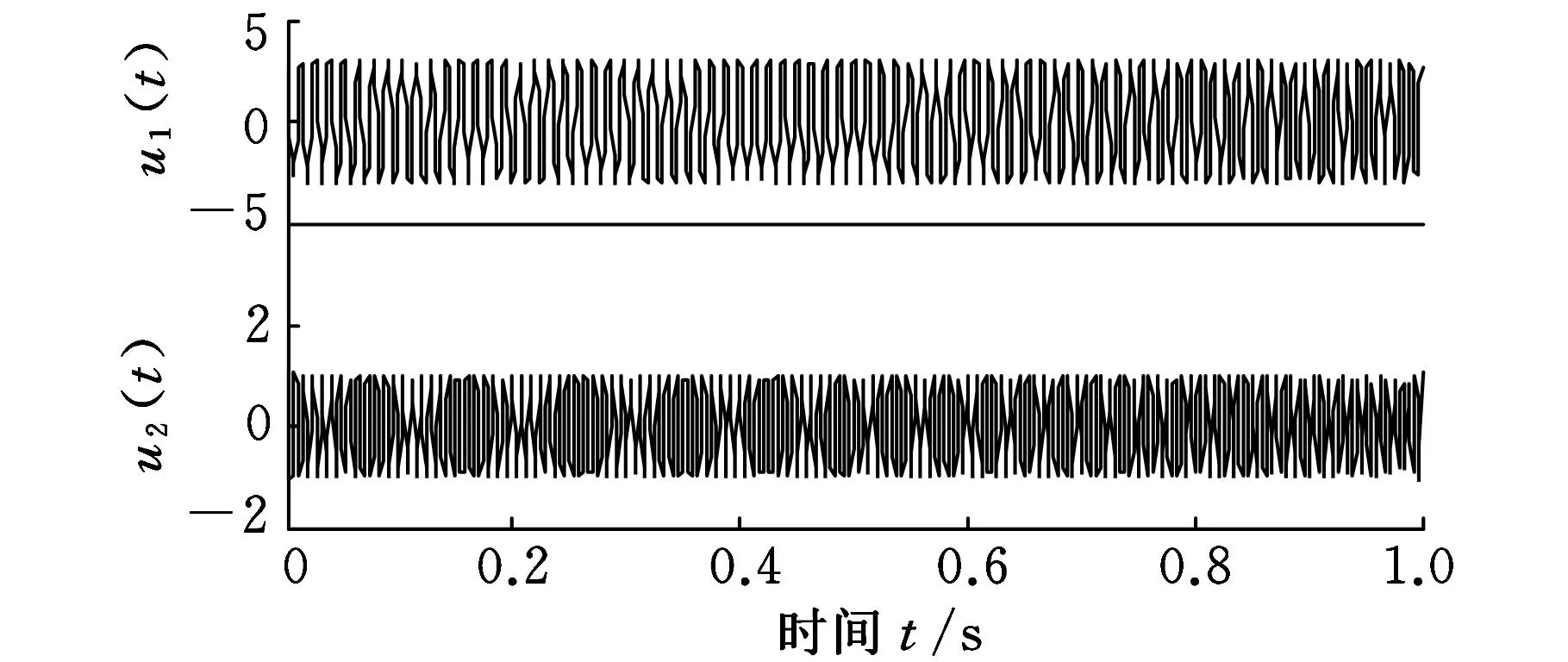
图2　仿真信号x(t)的ASTFA分解结果

在信号分解的过程中可以直接获得相位函数θ(t)，函数曲线如图3所示。按照式(10)获得解调相位函数s(t)，得到的各分量的解调相位函数：

s1(t)=19.161t3-12.822t2

(12)

s2(t)=19.296t3-13.022t2

(13)

同时给出解调相位函数的理论值：

(14)

图3　ASTFA方法得到的相位函数

方便起见，将各分量的解调相位函数与理论值曲线在同一坐标系下进行对比。从图4可以看出，3条曲线基本完全重合，说明由ASTFA方法得到的解调相位函数完全正确。

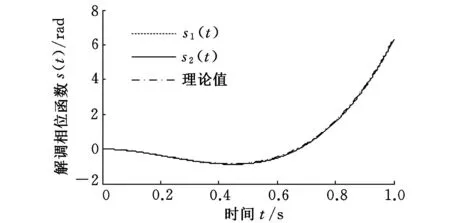
图4　解调相位函数曲线对比图

利用解调相位函数s1(t)、s2(t)对分量信号进行广义解调，将广义解调后的信号叠加混合并进行频谱分析，得到的幅值谱如图5所示。式(11)给定的仿真信号x1(t)、x2(t)的载波频率为79.6Hz和127.4Hz。图5中峰值频率为80Hz、128Hz，与载波频率接近，说明基于ASTFA的广义解调方法能有效地对多分量调频信号进行解调。

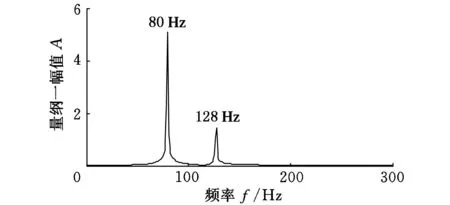
图5　广义解调后的分量信号的幅值谱

为进一步说明基于ASTFA的广义解调方法对频率调制信号解调的有效性，我们对仿真信号的频率进行分析。给出仿真信号的理论瞬时频率曲线(图6)、由ASTFA方法分解直接得到的瞬时频率曲线(图7)。通过频率对比分析可知，由ASTFA方法获得的瞬时频率与理论值基本相同，表明ASTFA能有效分解多分量频率调制信号。由广义解调后的叠加混合信号的Hilbert谱(图8)可知，经过广义解调后的信号的时频分布为平行于时间轴的直线，实现了信号的平稳化。以上分析表明，基于ASTFA的广义解调方法可对多分量的频率调制信号实现有效分解并将分量信号变为平稳信号。

图6　仿真信号x(t)的理论瞬时频率

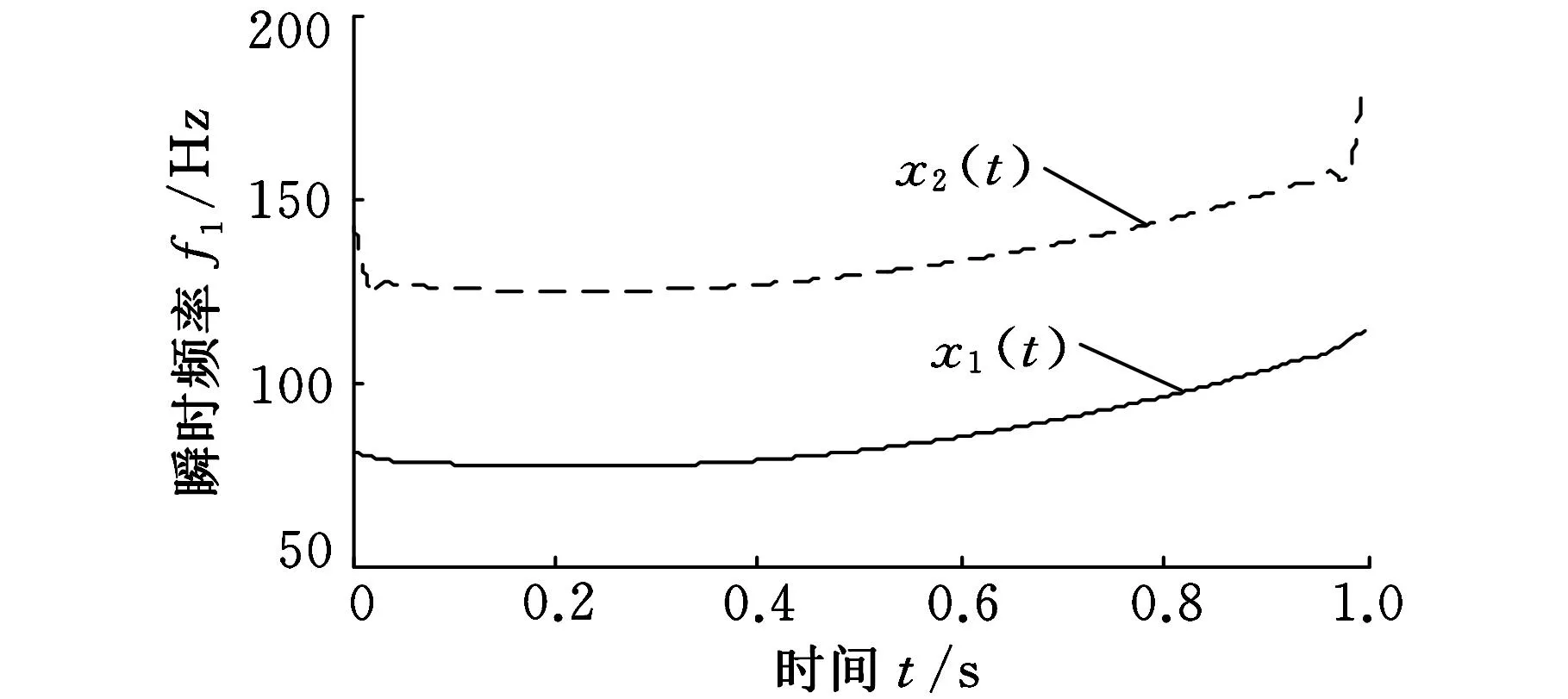
图7　ASTFA方法得到的瞬时频率

3应用实例

3.1滚动轴承的故障特征

假设滚动体与内外圈之间为纯滚动接触，轴承外圈故障特征频率为

(15)

内圈故障特征频率为[15]

(16)

式中，f为轴的转频；Z为滚动体个数；d为滚动体直径；D为轴承节径；α为接触角。

从式(15)、式(16)可以看出，特征频率与轴的转频间存在固定的比例关系，比例由轴承本身的特性决定。当转速非平稳时，滚动轴承的故障特征频率与轴的转频都是非平稳的。因此，当转速非平稳时，可以采用广义解调方法对信号进行平稳化处理。但是，当滚动轴承存在故障时，其振动信号还表现为多频率调制特性，而且在广义解调之前还需要确定解调相位函数。因此，基于ASTFA的广义解调方法适用于变转速工况下的滚动轴承非平稳信号处理。

3.2实验信号分析

如图9所示，在实验台上进行具有外圈故障、内圈故障的滚动轴承瞬态实验。轴承为6307型，利用激光分别在外圈和内圈上切割宽0.15mm、深0.13mm的槽来模拟故障。在轴承座上采集振动加速度信号，为了便于观察与验证，采用光电式转速传感器采集转速信号。

3.2.1外圈故障分析

外圈故障实验的主轴转速如图10所示，转速由809r/min升为1281r/min，转速非平稳。振动信号如图11所示，图中存在明显的冲击脉冲，但无法判定是否为外圈故障冲击。

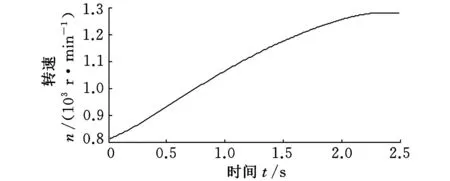
图10　外圈故障主轴转速信号

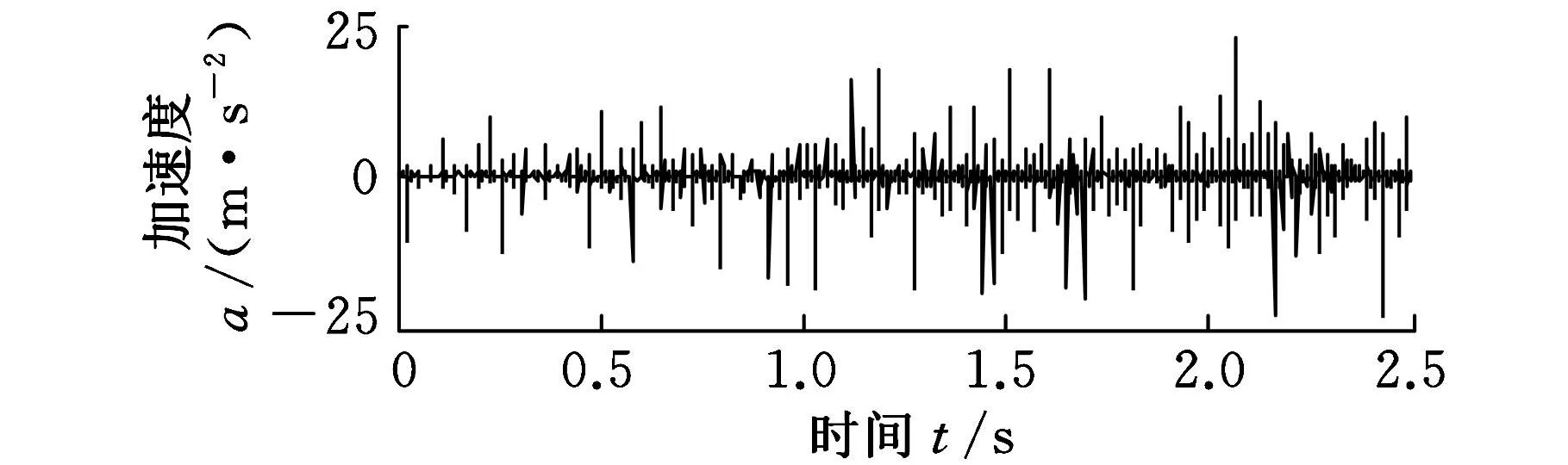
图11　滚动轴承外圈故障振动信号

对图10所示的转速信号进行广义解调，可以得到广义解调后的转频13.07Hz，根据式(15)得到滚动轴承的外圈故障特征频率39.99Hz。采用基于ASTFA的广义解调方法对图11所示的振动加速度信号进行分析，得到的分量信号如图12所示，得到的相位函数如图13所示，根据式(9)计算得到的解调相位函数如图14所示。采用图14所示的解调相位函数s1(t)、s2(t)、s3(t)对相对应的3个分量信号u1(t)、u2(t)、u3(t)进行广义解调，并对广义解调后的合成信号进行FFT分析得到频谱，如图15所示。从图15可以看出，在滚动轴承外圈故障特征频率及其2倍频处具有明显的峰值，表明基于ASTFA的广义解调方法能够有效提取滚动轴承外圈故障特征。

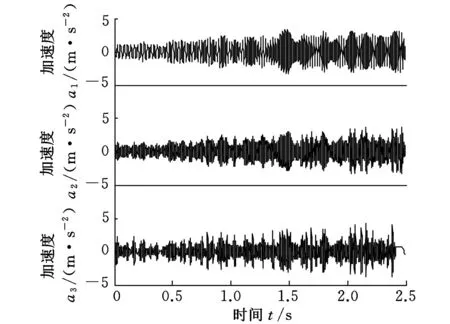
图12　滚动轴承外圈故障振动信号ASTFA分解结果

图13　ASTFA方法得到的外圈故障相位函数

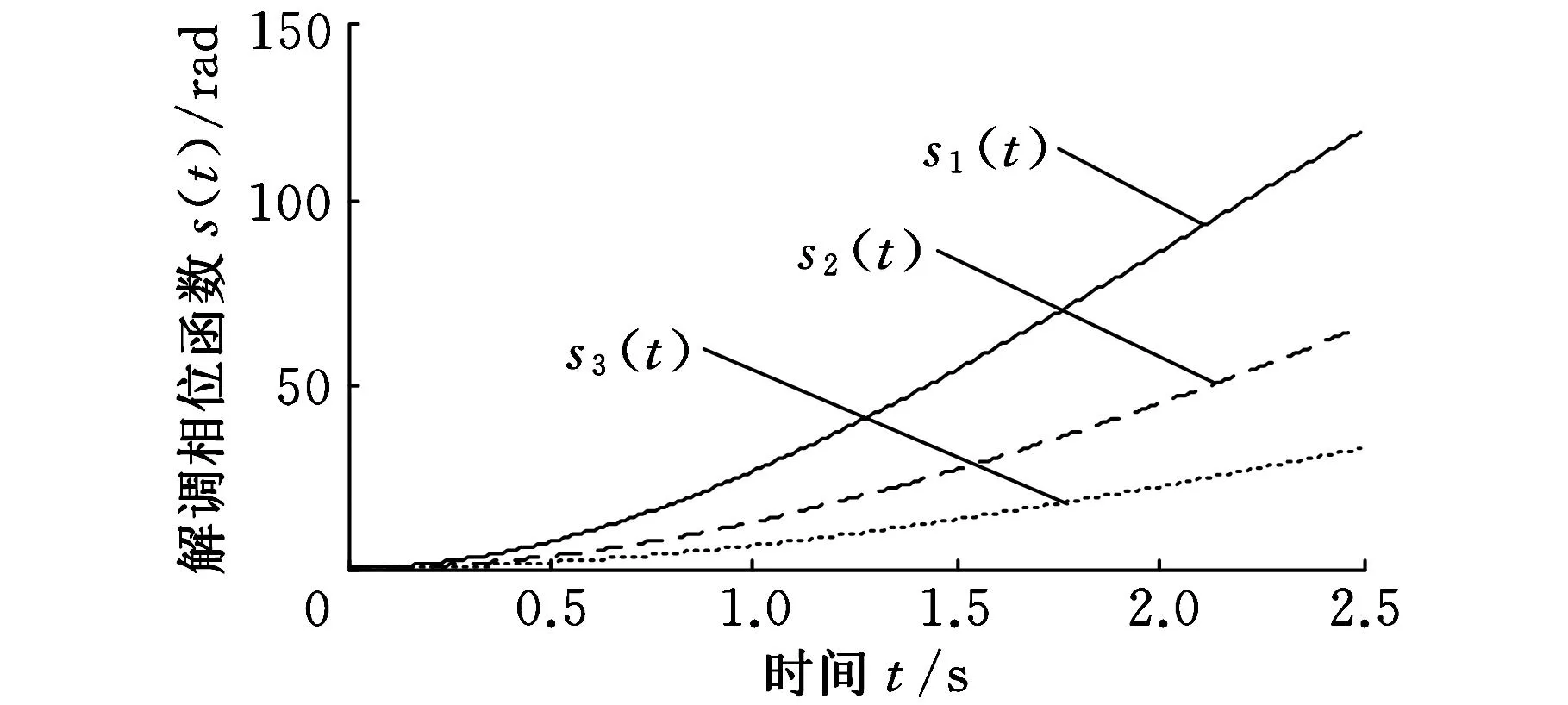
图14　外圈故障解调相位函数

图15　外圈故障分量信号广义解调后的频谱(ASTFA)

图16　基于MCPP的广义解调方法的外圈故障频谱

采用文献[11]基于MCPP的广义解调方法对图11所示的信号进行分析，结果如图16所示。对比图15、图16可知，基于ASTFA的广义解调方法得到的故障特征频率及其2倍频更接近于理论值，准确度更高。

3.2.2内圈故障分析

内圈故障实验的主轴转速如图17所示，转速由714r/min降为532r/min。振动加速信号如图18所示。对图17所示的转速信号进行广义解调，可以得到广义解调后的转频11.9Hz，根据式(16)得到滚动轴承的内圈故障特征频率58.8Hz。采用基于ASTFA的广义解调方法对图18所示的振动加速度信号进行分析，得到的分量信号如图19所示，得到的相位函数如图20所示，根据式(10)计算得到的解调相位函数曲线如图21所示。

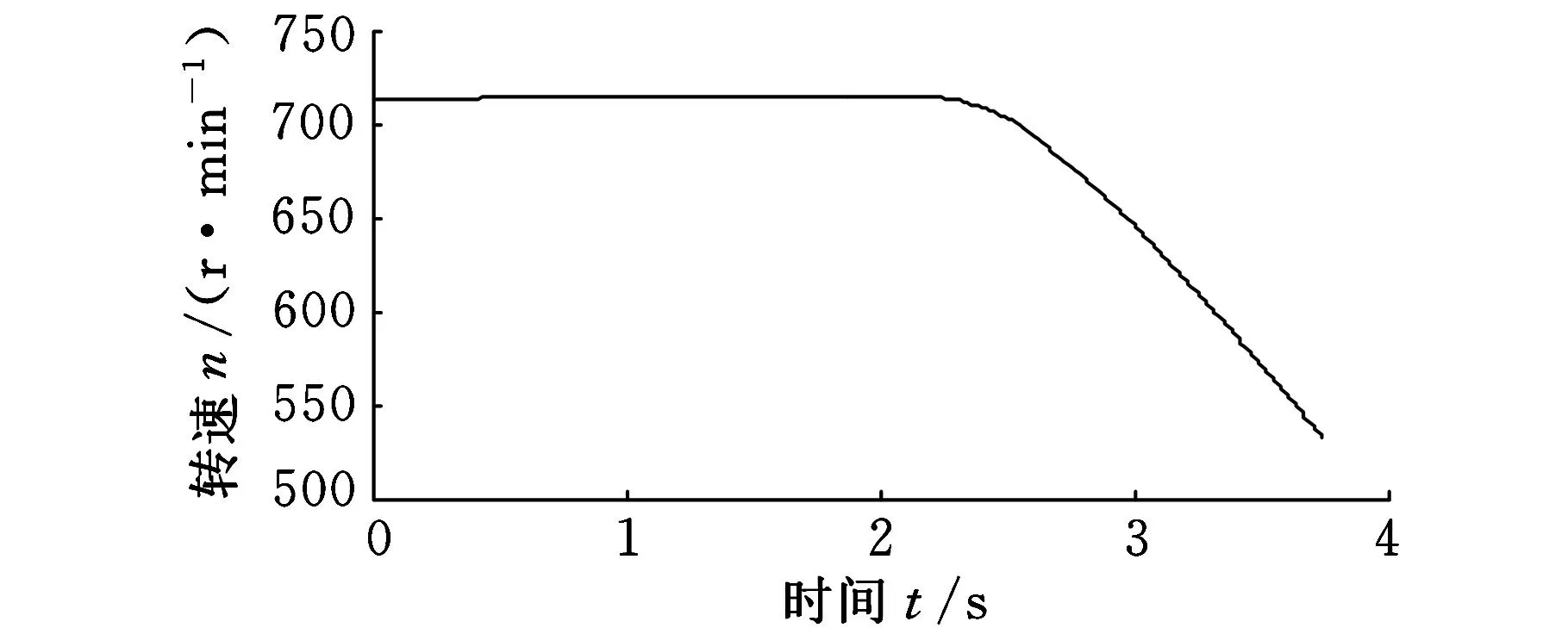
图17　内圈故障主轴转速信号

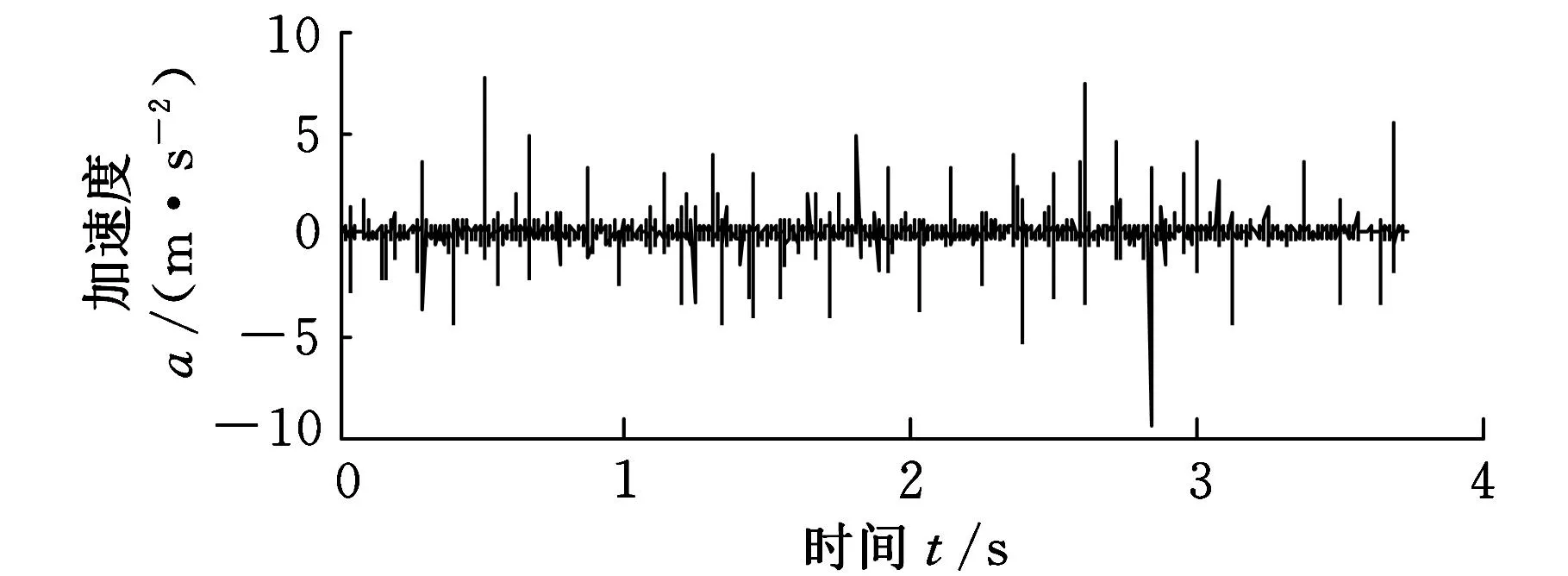
图18　滚动轴承内圈故障振动信号

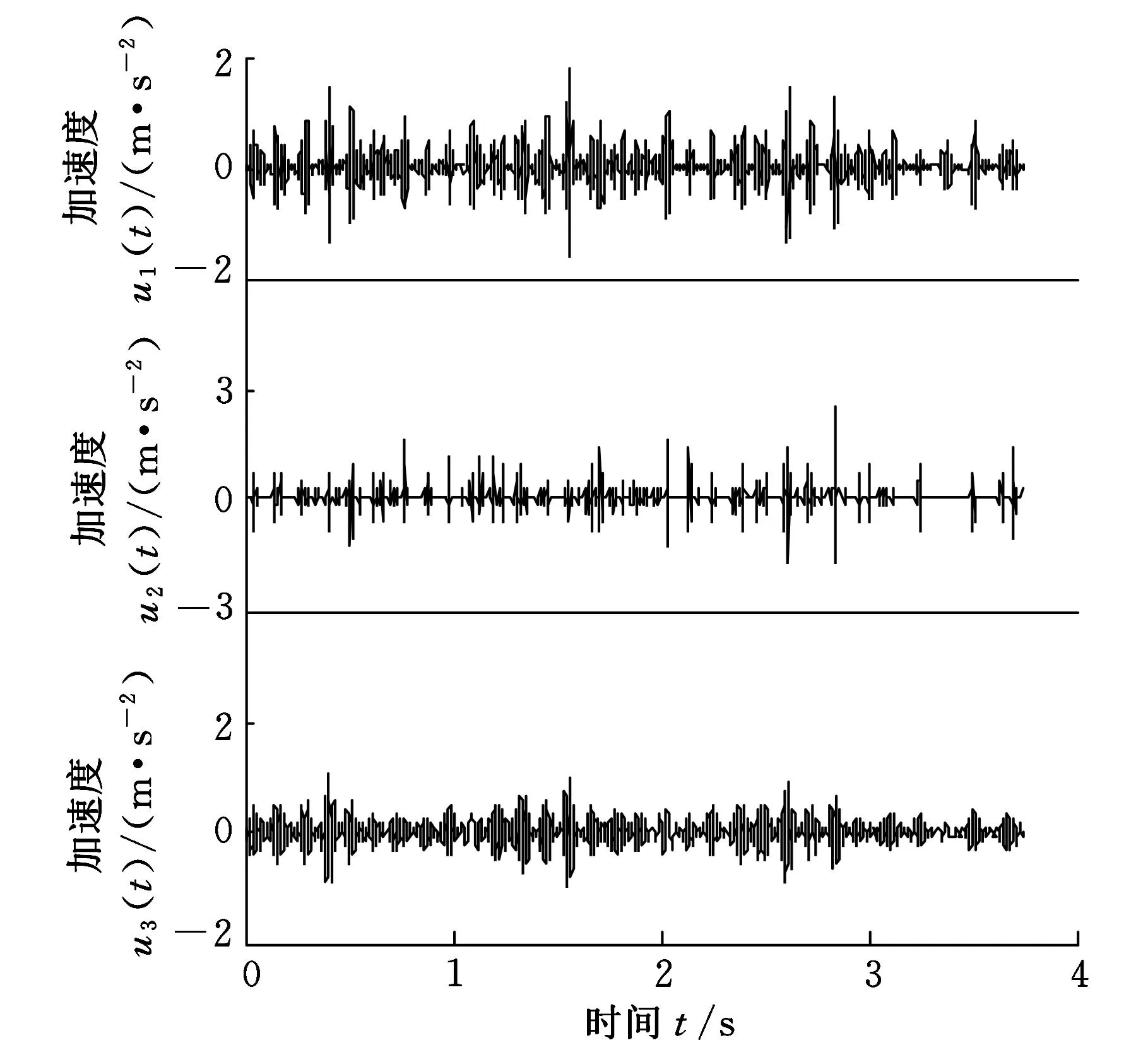
图19　滚动轴承内圈故障振动信号ASTFA分解结果

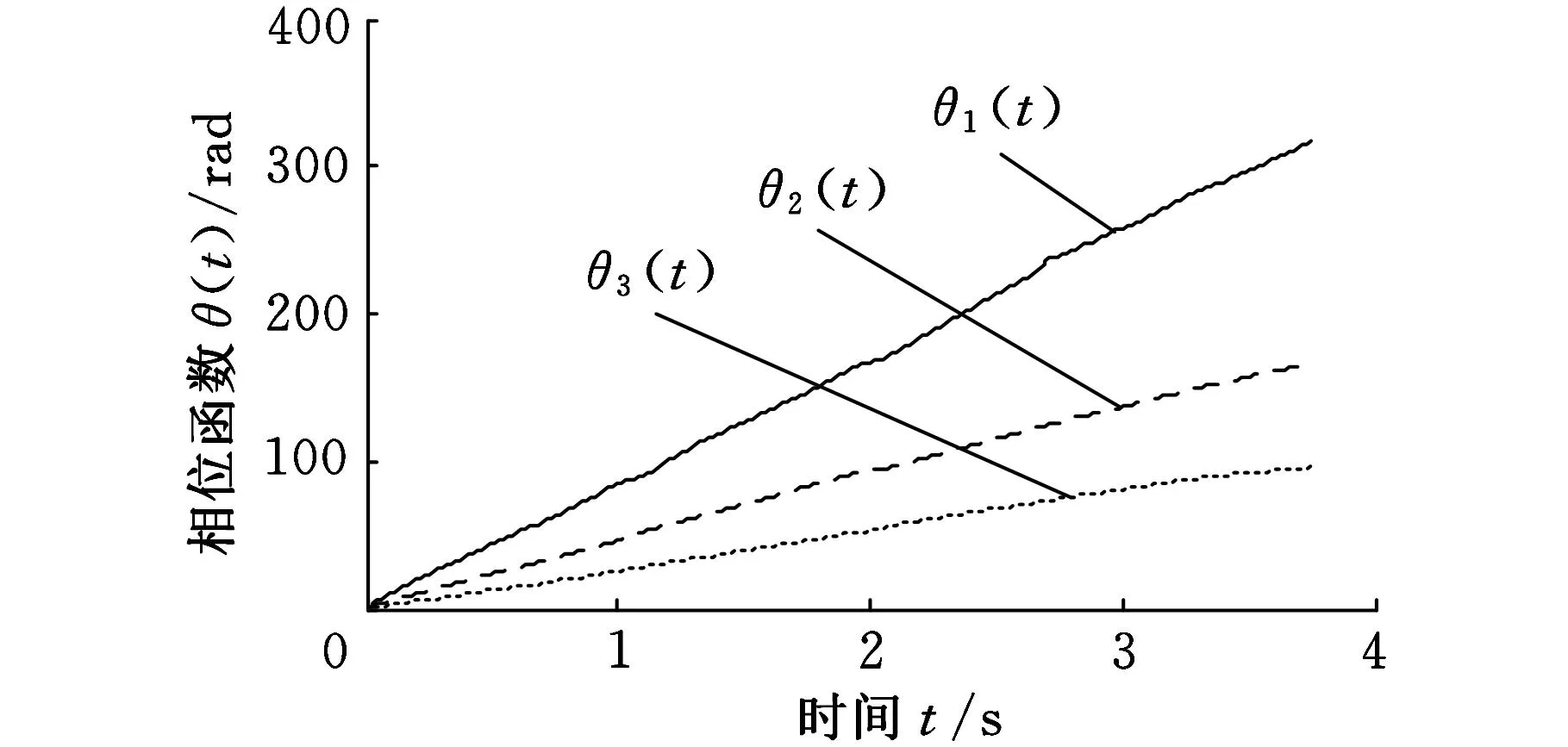
图20　ASTFA方法得到的内圈故障相位函数

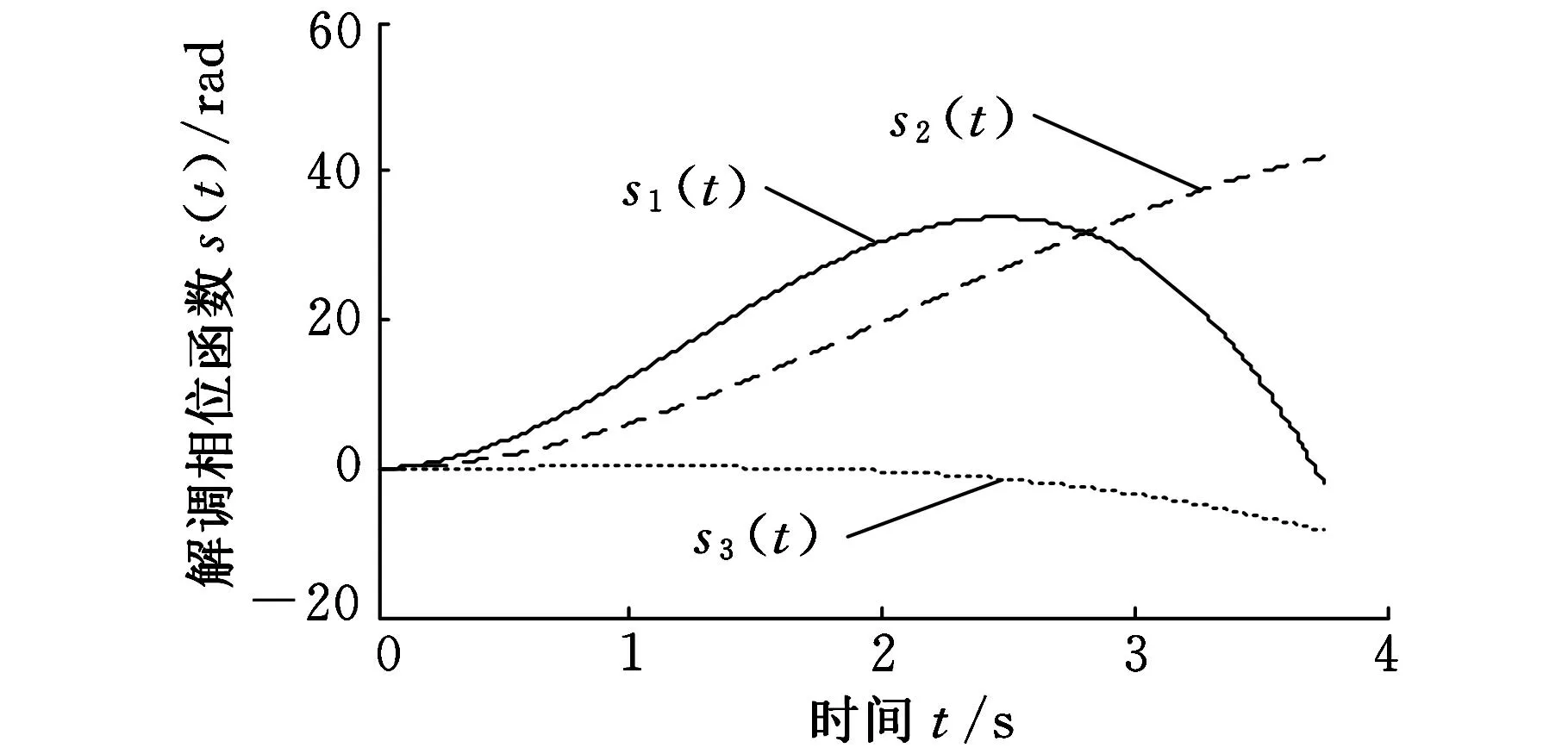
图21　内圈故障解调相位函数

图22　内圈故障分量信号广义解调后的频谱(ASTFA)

采用图21所示的解调相位函数s1(t)、s2(t)、s3(t)对相对应的三个分量信号u1(t)、u2(t)、u3(t)进行广义解调，并对广义解调后的合成信号进行FFT分析得到频谱，如图22所示。从图22可以看出，在滚动轴承内圈故障特征频率处具有明显的峰值，表明基于ASTFA的广义解调方法能够有效提取滚动轴承内圈故障特征。

类似于外圈故障，同样采用文献[11]基于MCPP的广义解调方法对图18所示的信号进行分析，结果如图23所示。从图23可以看出，图中存在明显的故障特征峰值频率55Hz，但是图示的故障特征频率与理论值相比偏差较大。因此，基于ASTFA的广义解调方法得到的故障特征频率更接近于理论值，准确度更高。

图23　基于MCPP的广义解调方法的内圈故障频谱

对比图22、图23还可以看出，图23中存在明显的2倍频及近3倍频的峰值，但是图22中并无明显的转频峰值。出现这种情况的主要的原因是，ASTFA方法基于最优化方法实现信号的分解，当满足收敛条件时才能够实现信号的分离。对于滚动轴承内圈故障来讲，滚动轴承故障振动信号与主轴旋转振动信号混杂在一起。采用ASTFA方法进行分解时，转频信号与故障信号的收敛条件并不一致，因此ASTFA可以准确地提取到滚动轴承的故障振动信号。多尺度线调频基稀疏信号分解是基于多尺度线调频原子的匹配追踪方法，本质上是利用多个基函数对信号进行分段表示，从而实现信号的分离。因此，其在对信号进行分段描述时无法将比较明显的转频信号完全分离。

4结语

ASTFA方法作为一种新的自适应时频分析方法能有效地对多分量频率调制信号进行解调，并且在实现信号分解的过程中直接获得相位函数，提取其二次项及高次项就可得到广义解调方法所需的解调相位函数。

相比于其他的解调相位函数估计方法，由ASTFA得到的解调相位函数更加准确，更彻底地解决了广义解调时频分析方法中相位函数的选择问题，提高了广义解调方法的应用性。实验分析结果表明，基于ASTFA的广义解调方法能够有效提取变速工况下的滚动轴承故障特征信息，具有一定的应用价值。

但是，ASTFA方法在计算效率上存在一定的不足，由于其基于最优化方法实现信号的分解，因此计算效率较低。若原始信号为N维向量，则ASTFA需要同时对N个参数进行优化。当原始信号维数较大时，使用ASTFA进行信号分解会产生很大的计算量。在后续的研究中，需在ASTFA方法的快速算法上进行重点研究。

参考文献：

[1]王冬云，张文志．基于小波变换的滚动轴承故障诊断[J]．中国机械工程，2012，23(3)：295-298．

WangDongyun，ZhangWenzhi．FaultDiagnosisStudyofBallBearingBasedonWaveletPacketTransform[J].ChinaMechanicalEngineering，2012，23(3)：295-298．

[2]徐亚军，于德介，孙云嵩，等．滚动轴承故障诊断的阶比多尺度形态学解调方法[J]. 振动工程学报，2013，26(2)：252-259．

XuYajun，YuDejie，SunYunsong，etal．RollerBearingFaultDiagnosisUsingOrderMulti-scaleMorphologyDemodulation[J]．JournalofVibrationEngineering，2013，26(2)：252-259．

[3]康海英，栾军英，郑海起，等．基于阶次跟踪和经验模态分解的滚动轴承包络解调分析[J]．机械工程学报，2007，43(8)：119-122．

KangYajun，LuanJunying，ZhengHaiqi，etal．EnvelopeDemodulationAnalysisofBearingBasedonOrderTrackingandEmpiricalModeDecomposition[J].JournalofMechanicalEngineering，2007，43(8)：119-122．

[4]郭瑜，秦树人，汤宝平，等．基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报，2003，39(3)：32-36．

GuoYu，QinShuren，TangBaoping，etal．OrderTrackingofRotatingMachineryBasedonInstantaneousFrequencyEstimation[J].JournalofMechanicalEngineering，2003，39(3)：32-36．

[5]李蓉，于德介，陈向民，等．基于阶次分析与循环平稳解调的齿轮箱复合故障诊断方法[J]. 中国机械工程，2013，24(5)：1320-1327．

LiRong，YuDejie，ChengXiangmin，etal．ACompoundFaultDiagnosisMethodforGearboxBasedonOrderTrackingandCyclostationaryDemodulation[J].ChinaMechanicalEngineering，2013，24(5)：1320-1327．

[6]丛华，吴广平，饶国强，等．计算阶次分析中避免阶次混叠的滤波定阶方法及其应用[J]. 振动与冲击，2012，31(12)：42-44．

CongHua，WuGuangping，RaoGuoqiang，etal．AMethodtoAvoidOrderAliasinginCOTBasedonFiltering[J].JournalofVibrationandShock，2012，31(12)：42-44．

[7]OlhedeS，WaldenAT．TheHilbertSpectrumviaWaveletProjections[J]．Proc．R．Soc．London．A，2004，460(2044)：955-975．

[8]程军圣，杨宇，于德介．基于广义解调时频分析的多分量信号分解方法[J]. 振动工程学报，2007，20(6)：563-569．

ChengJunsheng，YangYu，YuDejie．AMulti-componentSignalDecompositionMethodBasedontheGeneralizedDemodulationTime-frequencyAnalysis[J].JournalofVibrationEngineering，2007，20(6) ：563-569．

[9]杨宇，程军圣，于德介. 广义解调时频分析方法中的若干问题探讨[J]. 振动与冲击，2008，27(2)：19-24．

YangYu，ChengJunsheng，YuDejie．StudyonSomeProblemsintheGeneralizedDemodulationTime-frequencyAnalysisMethod[J].JournalofVibrationandShock，2008，27(2)：19-24．

[10]张晓菲，刘振兴，陈栋．基于广义解调时频分析的多分量复杂信号分解方法[J]．数据采集与处理，2012，27(5) ：630-634．

ZhangXiaofei，LiuZhenxing，ChenDong．Multi-componentandComplicatedSignalDecompositionMethodBasedonGeneralizedDemodulationTime-frequencyAnalysis[J].JournalofDataAcquisition&Processing，2012，27(5) ：630-634．

[11]任凌志，于德介，彭富强．基于多尺度线调频基稀疏信号分解的广义解调方法及其在滚动轴承故障诊断中的应用[J]. 中国电机工程学报，2010，30(11)：102-108．

RenLingzhi，YuDejie，PengFuqiang．GeneralizedDemodulationMethodBasedonMulti-scaleChirpletandSparseSignalDecompositionandItsApplicationtoRollerBearingFaultDiagnosis[J]．ProceedingsoftheCSEE，2010，30(11)：102-108．

[12]HouTY，SHIZQ．AdaptiveDataAnalysisviaSparseTime-frequencyRepresentation[J]．AdvancesinAdaptiveDataAnalysis，2011，3(1/2)：1-28．

[13]HouTY，ShiZQ．Data-drivenTime-frequencyAnalysis[J].AppliedandComputationalHarmonicAnalysis，2013，35(2)：284-308．

[14]MascarenasD，CattaneoA，TheilereJ，etal．CompressedSensingTechniquesforDetectingDamageinStructures[J].StructuralHealthMonitoring，2013，12(4)：325-338．

[15]钟秉林，黄仁．机械故障诊断学[M]．北京：机械工业出版社，2006．

(编辑张洋)