室温下Hg与镀银基板反应型润湿动力学研究

黄伟超，朱定一

(福州大学材料科学与工程学院，福建福州 350116)

0 引言

液态金属在基板上的润湿问题是材料科学及物理科学领域的重要问题，目前关于金属液滴润湿方面的研究主要集中在金属熔体与固相的润湿行为，这一重要物理化学现象在很大程度上决定了材料的制备可能性和最终使用性能．由于Hg是常温下唯一的液态金属，且该实验体系避开了高温润湿性实验中高温保护性气氛不易控制与高温摄像等难题，能够清楚观察和拍摄到反应型润湿行为动态过程．21世纪初，以Hg为对象的室温下反应型润湿行为的研究逐渐成为反应型润湿研究的热点之一．

Be’er等［1－2］对室温下Hg液滴在Ag基板上的反应润湿现象的铺展特性进行研究，并建立一种描述Hg与Ag反应的铺展过程模型．通过这一模型与实验现象相比较，认为Hg与Ag反应动力学过程除了有反应控制之外还可能存在其他控制因素，但是这一观点并未通过实验数据来进行验证．本文在此基础上做了更加深入的研究，通过将实验的主要参数(如初始接触角、终态接触角、铺展时间等)与四种国内外常见的动力学模型进行结合，得到各模型所对应理想条件下的理论实验数据，并与实验得到的实际数据相比较，可以直观地观察到各模型与实验数据的相似程度，从而为描述该反应润湿实验过程提供依据．

目前提出的动力学模型主要有:由 Voinov［3］提出，经 Cox［4］，Hoffman［5］和 Tanner［6］等扩展得到的流体动力学模型;基于Eyring［7］提出的绝对反应速率理论，之后由Blake［8－9］推导得到的经典分子动力学模型;由Eustathopoulos［10］课题组首先提出的线性铺展模型，之后由Dezellus等［11］通过新假设推导得到的近线性铺展模型，统称为化学反应控制模型;以及最早由Mortensen等［12］提出且用来解决液态二元合金在固体基板上的润湿问题的扩散控制模型．

本文通过Hg在镀银基板上的反应润湿实验，将实验获得的θ－t数据作为评判的标准，代入四种常见模型的动力学公式中，与实验结果进行比较，选取理论数据与实验数据相符的阶段，即可认为润湿过程在这一阶段符合该模型的动力学机制．

1 试验材料与方法

1．1 试验材料

基板材料选用20 mm×20 mm×1．5 mm镀银基板(基体为铜)，镀银基板中银层厚度约为5μm，其中银层纯度为99%．液体材料选用纯Hg(纯度为99．99%)．

1．2 接触角测量方法

实验所用仪器为SL200ABD型接触角仪，该仪器利用滴定法(dispensed drop method)原理，通过高速连拍摄像头记录接触角的变化，实验温度为室温25℃，Hg液滴体积约为1μL，每间隔0．2 s拍摄一幅图像，拍摄时长为10 min．图1是滴定法测量接触角的原理图．

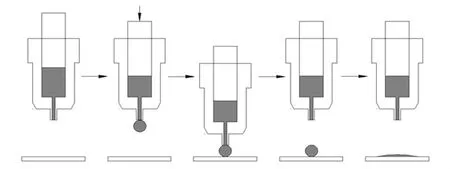
图1 滴定法测量接触角原理图Fig．1 Schematic presentation of dispensed drop method

通过ImageJADSA接触角测量软件［13］测量并记录接触角大小同时记录对应时间．

1．3 数据计算分析方法

首先将实验获得的接触角θ与时间t的数据绘制成θ－t关系曲线，其次通过流体力学模型、分子动力学模型和扩散控制模型三种动力学公式计算出θ与时间t之间的理论模型曲线，再将实验曲线与理论计算结果进行对比分析．Kim等［14］经过对几种经典动力学模型推导，得到θ－t之间的三种动力学模型如下:

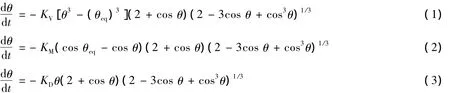
式(1)为流体力学控制模型，其拟合参数为KV;式(2)为分子动力学模型，其拟合参数为KM;式(3)为扩散控制模型，其拟合参数为KD;θeq为终态接触角;θ为任意时刻的瞬时接触角．

公式(1)～(3)均为瞬时接触角对时间的一阶导数式，为解出某一时刻对应的θ，需要通过数学上的四阶Runge－Kutta算法对该一阶导数式进行积分．

将四阶Runge－Kutta算法编译成Matlab程序，在其中输入不同模型的一阶导数式，初始条件下初始态接触角θ0，选取某一时刻t及该时刻接触角θt作为边界条件，及终态接触角θeq，选取合适的拟合参数，使t时刻计算得到的理论接触角与实验接触角θt相一致，便得到完全符合该模型时接触角和时间的数据．

由于爆珠工艺废水含有高达10000mg/L的石蜡油，3种废水混合后废水油类含量需低于30mg/L，因此必须对该废水进行预处理，防止废水含油量过高影响生物反应，因此，需采用撇油+隔油装置进行预处理。

式(4)表示Dezellus等［11］提出的反应控制动力学公式:

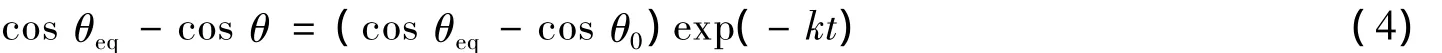
其中k为动力学常数，单位为s－1．对式(4)两边取对数:

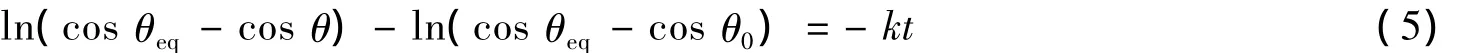
将实验测得的接触角θ与时间t代入到公式(5)中，如果实验计算得到的ln(cosθeq－cosθ)－t关系曲线成直线，则说明实验数据与反应控制模型规律相一致．

2 实验结果与分析

2．1 Hg在镀银基板上接触角的变化

当t0=0时，Hg在Ag表面上的初始态接触角为θ0，经过三次实验测定取平均值，θ0=131．74°．图2为Hg液滴在镀银基板上润湿过程．

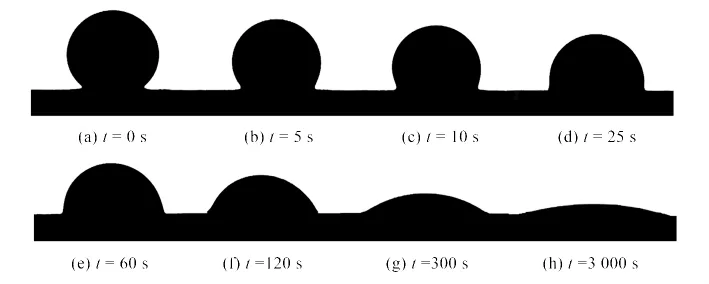
图2 Hg液滴在镀银基板上润湿过程Fig．2 Schematic sequence of mercury droplet spreading on thin silver films

图3为Hg在镀银基板铺展过程θ－t关系曲线．可以看到接触角在30 s内快速变化，由初始态131．74°变化为 87．49°，Hg 在镀银基板表面发生剧烈反应，之后反应逐渐趋于稳定，因此接触角变化速度逐渐变慢，在经过足够长时间润湿后发现，液滴完全铺展到整个基板表面，最终接触角接近于0，因此Hg在镀银基板上的润湿实验属于完全润湿．

2．2 不同动力学模型的计算结果与实验结果对比

绘制流体力学模型、分子动力学模型和扩散控制模型理论θ－t关系曲线所需参数:初始条件下初始态接触角θ0=131．74°，边界条件t=600 s时接触角为13．84°，终态接触角为0．将实验接触角θ与时间t代入公式(5)中，应用反应控制模型绘制出ln(cosθeq－cosθ)－t关系曲线．图4所示为通过四种常见动力学模型计算得到的理论关系曲线与实验关系曲线的比较．其中(a)～(c)为θ－t关系曲线，(d)为ln(cosθeq－cosθ)－t关系曲线．

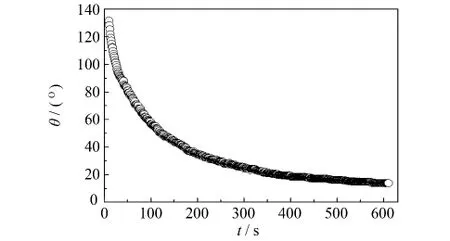
图3 室温下Hg/镀银界面反应的接触角θ时间t的关系曲线Fig．3 Variations in contact angle with time during mercury droplet spreading on silvering substrate in room temperature

通过图4(d)中ln(cosθeq－cosθ)－t实验关系曲线，发现在0～150 s时间内按界面反应动力学模型计算，理论计算结果与实验结果高度一致，线性拟合度达到R2=0．994 26．表明在Hg/Ag界面的反应前期阶段，铺展受到的主要控制因素为界面反应控制．

图4(c)中θ－t理论曲线和实验曲线在150～600 s内变化规律完全一致，其中拟合参数KD=6．201×10－3．表明Hg在镀银基板上反应润湿时，在150～600 s内完全符合扩散控制模型，在此阶段Hg液滴的铺展受到扩散控制因素的影响．

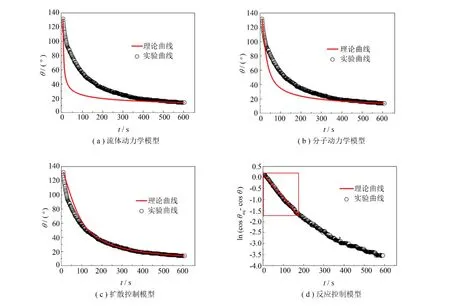
图4 动力学模型计算得到的理论关系曲线与实验关系曲线Fig．4 The theory curve by using four familiar wetting dynamics models in contrast to the experimental curve

2．3 Hg在镀银基板上的润湿机理

根据上述分析结果，认为实际反应润湿现象由多种控制因素共同作用，一种反应动力学模型不能完全描述反应润湿的整体过程，Dezellus等［15］将Cu－40%Si合金在石墨基板表面反应润湿的实验结果与反应控制模型对比时，同样发现在实验初始阶段0～500 s内ln(cosθeq－cosθ)－t实验关系曲线线性拟合度较好，但实验后期与模型相差很大．此外，反应润湿过程中存在多种控制因素，但某阶段只表现出一种动力学规律．这是由于反应润湿过程中各阶段存在主要控制因素，接触角θ和时间t的关系遵循该控制因素对应的动力学模型规律．

结果表明，Hg在镀银基板上的反应润湿过程在初始阶段0～150 s内主要控制因素为反应控制．实验后期150 s后主要控制因素转变为扩散控制．以该结论对Hg在镀银基板上反应润湿过程进行描述，如图5所示．

第一阶段(图5a)为液滴接触基板初期，此时Hg在镀银层表面发生化学反应生成Ag2Hg3，固液界面上Hg原子和Ag原子数量充足，三相接触线处反应元素扩散比界面反应更易进行，根据主要控制因素由体系中最慢的环节来决定，此时化学反应为主要控制因素．

第二阶段(图5b)为固液界面生成反应产物，反应产物层厚度逐渐增加，形成双球冠模型［16］．此时，参与反应的元素从液相往三相线处的扩散速率快于三相线局部区域内化学反应的速率．即反应元素的供给速率要快于三相处的反应速率．因此，主要控制因素仍为化学反应控制．

第三阶段(图5c)反应产物Ag2Hg3厚度逐渐与Ag镀层厚度相同，Ag镀层基板与Hg不发生反应，因此，反应产物厚度不能继续增加，反应产物层开始由纵向生长转变为横向扩展．此时三相接触线处仍为反应控制．

第四阶段(图5d)反应产物层半径超过三相接触线，在三相接触线周围距离l处出现圆环，称为晕圈现象［1］．此时三相接触线区域的Hg与未反应的Ag层之间存在一定厚度的反应产物，Hg原子在反应产物内部扩散与Ag层反应，使铺展继续进行．此时Hg原子在固体中扩散，扩散速率变慢，Hg/Ag反应速率固定，扩散速率小于反应速率，因此主要控制因素转变为扩散控制．

图5 Hg在镀银基板上铺展原理图Fig．5 Schematic sequence of mercury droplet spreading on silvering substrate in room temperature

3 结语

1)反应润湿过程的影响因素复杂，通过一种模型进行分析，会出现实验数据只有部分符合模型的问题，无法描述实验数据整体变化规律．本文通过对四种不同机制的动力学模型计算，找到与实验结果一致的部分，得到反应润湿过程中不同阶段的动力学规律．

2)Hg在镀银基板上润湿实验中接触角与时间的变化规律在0～150 s内与近线性模型一致，在150～600 s内与扩散控制模型相一致，即反应润湿过程的控制因素由初始阶段的反应控制逐渐转变为扩散控制．