隧道下穿时基于傅里叶时间序列预测临近结构沉降发展

沈 圣，肖 力，张 浩

(1．福州大学土木工程学院，福建福州 350116;2．石家庄铁道大学土木工程学院，河北石家庄 050043)

0 引言

随着我国城市化进程的不断加快，修建地铁隧道来缓解人口密集带来的交通压力成为经济和社会发展的必然选择．由于市政规划的复杂性，修建隧道必然会穿越一些重要结构物．大量的现场观测表明，隧道下穿会使周边结构物产生不均匀沉降，沉降严重时将影响到结构物的安全，因而需要根据穿越期内结构物沉降的发展来控制隧道穿越速度．目前结构沉降监测的报警阈值多设定为沉降总量超限，以及日平均或最大沉降速度超限［1－2］，但由于隧道与结构之间存在一定厚度的土层，结构沉降的发展必然滞后于下部隧道的掘进，也就是说仅凭当前沉降观测值判定结构的安全性，存在滞后的可能．另外，目前规范对穿越期现场人工监测频率仅规定为每天1～2次［1－2］，若沉降突变发生在本期观测结束、下期沉降观测尚未进行这个时间段内，沉降观测的预警目的就无法实现．针对这两个问题，一个较好的解决方案是基于当前沉降数据对本期观测结束、下期沉降观测尚未进行这个短期时间段内的结构沉降(后文简称短期沉降)发展进行预测，这样可以尽可能早地获知未来可能发生的沉降突变，以此评估结构未来的安全状况并采取必要预防措施，在一定程度上弥补传统沉降预警时间滞后的缺点．

对于结构沉降预测，目前的研究主要集中在监测数据足够充分、沉降趋势相对明确的长期沉降上，相继提出了固结度对数配合法(即三点法)、双曲线法［3］、Verhulst曲线法(也称为Logistic生长模型法)［4］、Asaoka法［5］、神经网络法［6］、基于自回归与滑动平均模型的时间序列法［7－8］等．但将上述方法直接移植于结构短期沉降预测则不可行．原因是结构短期沉降具有与长期沉降相比明显不同的物理与数学特征:①环境因素对短期沉降的扰动作用更加显著，结构的长期沉降主要取决于外荷载和土体的固结特性，而短期沉降，特别是每日沉降，各种环境因素(如温度、湿度等)和偶然因素(如降雨等)也会导致沉降的明显改变;②与长期沉降相比，短期沉降更多地呈现出贫信息的特征，即有效观测值数量较少、已知数据波动较大，因而难以对已知数据的变化规律进行拟合分析和外推预测．对于第②点，目前仅有基于灰色关联度理论的GM(1，1)灰色模型［9］可用于贫信息条件下的预测，然而该模型进行预测时并未考虑“短期”这一条件所隐含的结构物理状态变化特征，故其预测精度还有进一步提升的余地．

首先，对某混凝土水库在临近地铁隧道右线穿越时若干关键点处的沉降进行逐小时的长期监测，通过分析沉降－时间曲线(s－t曲线)得到其反映出的结构状态变化特征．其次，提出了基于傅里叶时间序列(Fourier time series)的结构短期沉降的预测方法，简称FTS沉降预测法．最后，采用该水库在地铁隧道左线下穿时的沉降实测数据，对FTS沉降预测法和GM(1，1)灰色模型得到的沉降预测值的预测精度进行对比．

1 隧道下穿时结构短期沉降变化特征

无论何种预测方法，都需要建立在已知数据的变化规律基础上，方能保证较好的预测精度．由于现场人工测量频率较低，其数据无法全面反映24 h内沉降的变化规律．为此课题组在某市地铁隧道右线下穿临近一混凝土水库时，在水库关键区域布设静力水准系统(精度为0．01 mm)，每隔1 h测量一次，得到隧道下穿时水库沉降的逐小时变化数据．

该穿越于2012年秋季实施．沉降监测点与隧道空间关系如图1所示，其中1#、2#监测点分别位于约距隧道中线4倍直径的结构角点和隧道中线上方处，测量数据以向上运动为正．根据有限元模拟结果，2#测点受到隧道穿越的影响较大，1#测点也处于影响范围内．图2给出了两个测点在下穿全过程(528 h)的s－t曲线．从中发现，虽然测点沉降趋势相反，但两条曲线局部最大或最小值和距离其最近的两个局部最大或最小值之间的时间间隔大致相等．为此将沉降数据进行傅里叶变换，得到如图3所示的频谱图．由图3可见，频谱图上各阶频率基本成倍数关系，且1#测点沉降的第一、二阶频率与2#测点沉降的对应频率相等．这表明虽然测点位置不同，但各测点的短期沉降发展都受到同一个基频约为11．393μHz的周期性因素影响，相应的周期为87 773 s，相当于24．38 h．据此猜测，造成这种波动的最可能原因就是每日温度变化．

图1 沉降测点与隧道空间关系图Fig．1 Spatial relationships about the settlement monitoring points and the shield tunnels

图2 下穿全过程内结构沉降－时间(s－t)曲线Fig．2 Relationships between settlements and times in different monitoring points

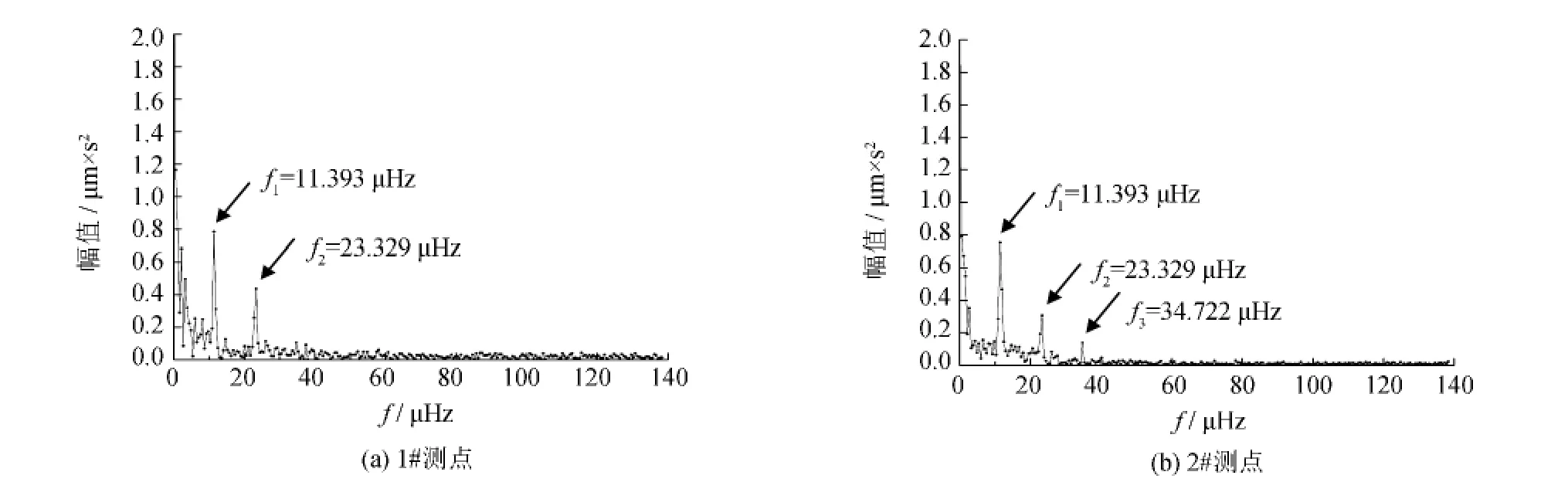
图3 沉降频谱图Fig．3 Frequency spectrum of settlements

分析图2两条曲线的整体趋势可知，1#测点总体向下沉降，2#测点总体往上隆起，每日沉降围绕趋势线上下波动，且波动幅度较大．若将随时间变化的沉降值视为时间序列，则该序列表现出明显的周期性和趋势性特征．时间序列理论指出，时间序列一般由长期趋势、季节变动、不规则变动构成［10］．在短期沉降预测问题中，季节变动即为温度循环导致的沉降波动，不规则波动即为沉降突变．但是，沉降突变一般都有一个发展过程，若将两次监测的时间间隔缩短至1 h甚至更小，沉降突变就可以视为长期趋势发生了改变．因此，只要沉降预测的时间间隔足够短，就可以认为短期沉降s仅由趋势项s1和周期项s2两部分构成．前者来源于盾构隧道下穿，为沉降发生的主要因素;后者体现了温度等周期性因素的影响，为沉降发生的次要因素．

2 基于傅里叶时间序列的临近结构短期沉降预测方法

考虑到隧道穿越期间人工测量沉降是不断进行的，基于傅里叶时间序列的临近结构短期沉降预测方法(FTS沉降预测法)的目标就集中在预测本次人工测量结束到下次测量发生前这一时间段内的沉降发展．

2．1 FTS沉降预测法

对于周期性时间序列，可按照周期对序列分段处理．对于本问题而言，采用多项式拟合中的分段线性拟合思想，可认为当分段取的足够小时，该段内沉降的趋势项s1可近似为线性函数:

式中:t为预测值所处时间;k、c为待定独立参数，其中c为常数．

该段内沉降的周期项s2可以通过傅里叶级数展开进行拟合:

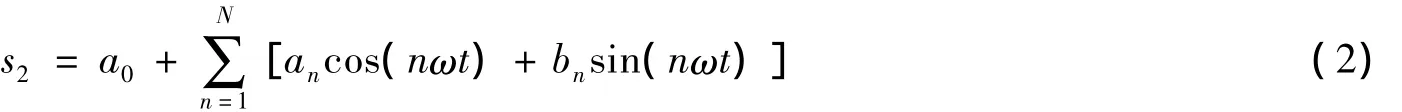
式中:a0、an和bn均为待定独立参数，其中a0为常数．

总沉降s=s1+s ，将式(1)、(2)代入得:

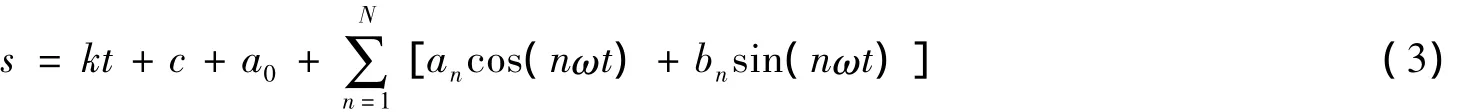
由于c和a0均为常数，可以合并为独立常参数d，式(3)即化简为式(4):

假定在p个等间隔时间点上时间t1=τ，t2=2τ，…，tp=pτ，τ为以小时为单位的时间间隔，各时间点上对应沉降为s1、s2、…、sp，将其代入式(4)，整理得:

式中:X={k，d，a1，b1，…，aN，bN}T，S={s1，…，sp}T．系数矩阵 B 的表达式为:

由于T=24 h，可得式(6)中ω=2π/T=π/12．

采用最小二乘法求解，则有:

注意若时刻t1=τ，t2=2τ，…，tp=pτ的取值使B的主元为0，(BTB)－1就不存在，可通过对时间轴进行整体平移来避免该问题．

2．2 计算过程中傅里叶展开次数N和已知数据数量p的确定

在实际工程预测中，N的取值不宜过高，这是因为:①N越大，待定系数的数量就越多，最小二乘拟合中使残差平方和小到一定程度所需要的数据个数就越多，则拟合函数对于沉降突变的灵敏度就越低;②沉降实测值也非绝对真值，而是含有一定的测量误差，对周期项的过度拟合有可能会放大测量误差的影响;③在一定条件下，无穷阶数的傅里叶级数可以无限逼近任意形式的周期函数，观察图2中曲线可知，任意周期内的曲线形状都较接近于正弦/余弦函数，较低的展开次数N即可对此类曲线取得不错的拟合精度．基于上述理由并为简化计算起见，本文令N=1，则式(4)和式(6)即可简化为:

已知数据数量p的取值也存在合适范围．为了满足最小二乘法使用条件以及对已知数据的拟合达到一定精度，要求p＞2N+2=4．同时，p的取值又不宜过大，这是由于当前沉降和已知沉降的相关性会随着时间间隔的增大而不断降低，如果相关性较低的数据在已知数据中所占比例较大，预测精度以及对沉降突变的灵敏度就会不升反降．因此在实际应用时，建议采用前期数据进行试预测以确定合适的p值．

2．3 预测模型的自修正

如前所述，当前沉降和已知沉降的相关性会随着时间间隔的增大而不断降低，即第p至(p+1)时刻之间的沉降与第p时刻的沉降值具有最大的相关性，而与第(p－1)、(p－2)、…、2、1时刻的沉降值相关性则是依次递减．故在预测第(p+1)至(p+2)时刻之间的沉降值时，在序列{(t1，s1)，(t2，s2)，…，(tp，sp)}中删除第一项(t1，s1)，增加最后一项(tp+1，sp+1)．在预测第(p+2)至(p+3)时刻之间的沉降值时，在序列中继续删除第二项(t2，s2)，增加最后一项(tp+2，sp+2)，后续可依次类推．这样做不仅可以保持已知数据序列和预测值之间的相关性，且可使已知数据序列长度不变，则预测方法的计算格式也就保持稳定不变．

3 工程实例检验

3．1 工程简介与检验方法设定

某箱型钢筋混凝土水库使用年限较久，且底板较薄．左、右线隧道与水库的平面关系如图1所示．底板与隧道之间的土层厚度约为9 m，以粘土和粉质粘土为主．继右线隧道下穿后，左线隧道下穿于2013年春季实施．采用有限元软件对左线隧道在水库底部穿越全过程进行了模拟，结果表明水库西墙中部和西南角处可能发生较大沉降．为避免隧道穿越期间水库底板开裂，采用静力水准系统对水库在左线隧道穿越期的沉降进行逐小时自动化监测，1#、2#测点布设如图1所示．在穿越期间也实施了间隔6 h的人工沉降观测．将自动监测数据中与人工观测时间一致的数据假定为已知实测数据，采用FTS沉降预测法对其余时间点沉降进行预测，并与实测沉降对比．为了检验FTS方法的预测效果，还采用了目前工程中较为常用的另一种预测方法——GM(1，1)灰色模型．GM(1，1)灰色模型是一种基于灰关联理论的预测方法，其基本步骤是先将无规则的数据序列变换成较有规律的序列(如近似于指数模型的序列)，再依据最小二乘准则将指数模型变换成微分方程形式，从而用微分拟合曲线比较准确地逼近数据序列，而此曲线的延伸即可认为是所求的预测值［9］．

2#测点在左线隧道下穿期内的s－t曲线如图4所示．由于数据较多，选取2个时长为24 h的时间段作为检测时段:A时段(157～180 h)为隧道穿过监测点后2天，模拟结果表明该时段内沉降趋势项(隆起)可能出现局部极值;B时段(325～348 h)当天有小寒潮，可能导致沉降波动项出现局部极值．通过前期平稳段沉降的试预测，发现当取N=1、p=8时预测误差绝对值基本小于0．15 mm，故在A、B时段预测时取系数N=1、p=8．

预测A时段中157～162 h的沉降值时，设定8个已知的沉降值为0．25 mm(114 h)、0．14 mm(120 h)、0．02 mm(126 h)、0．08 mm(132 h)、0．18 mm(138 h)、0．06 mm(144 h)、－0．07 mm(150 h)和 0．15 mm(156 h)，在预测163 ～168 h时，删除0．25 mm(114 h)，补入162 h时的沉降实测值0．21 mm，后续时段做法类同，依次补入沉降值为0．00 mm(168 h)和－0．07 mm(174 h)．预测B时段325～330 h的沉降值时，设定8个已知的沉降值分别为－0．09 mm(282 h)、－0．23 mm(288 h)、－0．33 mm(294 h)、－0．22 mm(300 h)、－0．39 mm(306 h)、－0．50 mm(312 h)、－0．50 mm(318 h)和 －0．25 mm(324 h)．后续补入的实测沉降数据依次为 －0．2 mm(330 h)、－0．52 mm(336 h)和 －0．54 mm(342 h)．另外，由于GM(1，1)灰色模型仅能预测与给定数据时间间隔相同的未来时刻沉降，故其它时刻预测数据采用线性插值给出．

图4 2#测点在左线隧道穿越期间s－t曲线Fig．4 Relationship between settlements and time in point 2

3．2 两种方法预测结果与实测沉降的对比及分析

图5给出了采用FTS沉降预测法与GM(1，1)灰色模型对两个时段沉降的预测值与沉降实测值的比较．两类沉降预测值的误差列于表1．从图5中可以看出，采用FTS沉降预测法得到的沉降－时间预测曲线与实际发生的沉降－时间曲线较为吻合，而采用GM(1，1)灰色模型得到的沉降－时间预测曲线则存在较大误差．将FTS沉降预测法与GM(1，1)灰色模型得到的沉降预测值与沉降实测值列于表1．对比数据可见，FTS沉降预测法给出的数据误差大都小于0．15 mm，而GM(1，1)灰色模型给出的数据误差大都超过了0．15 mm．进一步分析表明，A时段内FTS沉降预测法得到预测值中误差分布个数随误差值的增大呈递减趋势，在全部24组预测数据中，预测误差在0．05 mm以下的数据约达50%，75%的数据的误差在0．1 mm以下，而GM(1，1)灰色模型得到的预测值中误差分布个数随误差值的增大则呈递增趋势，预测误差在0．05 mm以下的数据仅占全部预测数据的15%，而超过50%的数据的误差大于0．1 mm．而B时段中的误差分布趋势与A时段基本相同．FTS沉降预测法给出的预测数据中有95%的数据误差小于0．15 mm，而GM(1，1)灰色模型给出数据中可达到上述精度的数据仅占全部数据的40%．

通过上述对比，可以认为在预测带有温度影响的结构短期沉降时，FTS沉降预测法的预测精度要高于GM(1，1)灰色模型．主要原因是GM(1，1)灰色模型的计算公式［9］从本质上而言还是一个近似的指数曲线模型计算．指数模型适用的一个重要前提是数据分布有较好的单调性，而结构短期沉降受到温度等周期性因素的影响，其单调性恰巧是比较差的．FTS沉降预测法也正是考虑了周期性的影响才能得到比较好的预测精度．

图5 采用两种方法得到沉降预测值与实测值对比Fig．5 Comparison between forecasting values by two methods and real values

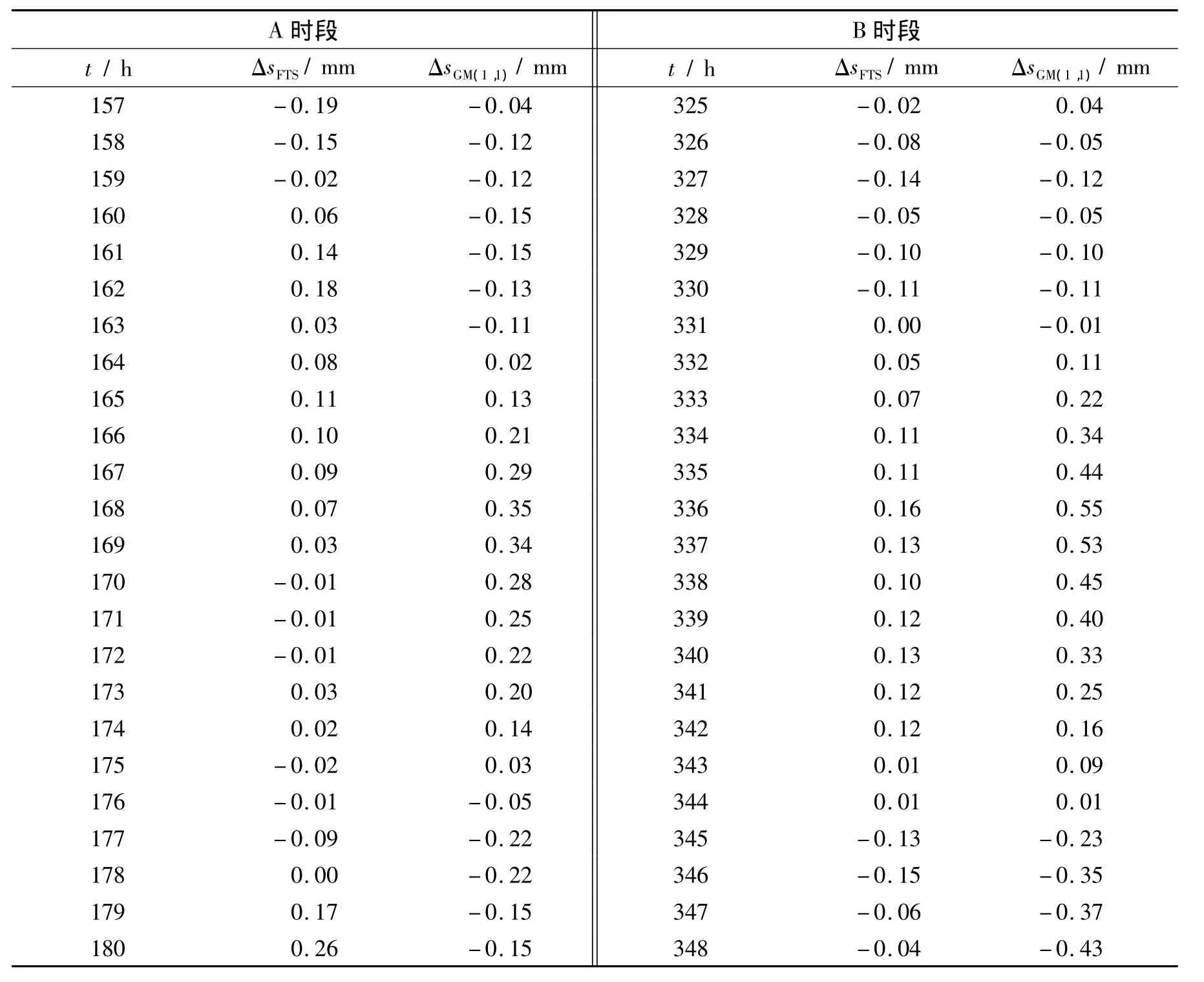
表1 两种沉降预测值与实测值的误差Tab．1 Differences between forecasting values by two methods and real values

另外，无论是FTS沉降预测法还是GM(1，1)灰色模型，B时段中误差要大于A时段．这是由于当温度剧烈变化时，结构沉降受到温度的影响就会明显增大，而已知数据所处时刻的温度波动并不明显，从而造成了误差的增加．

4 结论

1)测量了某地铁隧道右线下穿时，临近结构逐小时变化的沉降－时间曲线．曲线的分析结果表明，临近结构的短期沉降受到温度波动的显著影响，结构短期沉降应主要由隧道穿越引起的趋势项和温度波动导致的周期项组成．

2)根据上述特征，提出了基于傅里叶时间序列的短期沉降预测方法．该方法采用傅里叶级数和线性函数对周期项和趋势项分别进行拟合，相加即得短期沉降的总预测值．该方法对于未来沉降突变的灵敏度可由数据新陈代谢保证．根据沉降－时间曲线形状，建议傅里叶展开次数取为1，提出已知数据的数量不宜过小和过大，实际预测时可通过前期数据试预测确定．

3)采用同一结构在隧道左线下穿时的沉降实测数据对FTS沉降预测法和GM(1，1)灰色模型的预测精度进行比较．结果表明，FTS沉降预测法对结构短期沉降的预测精度高于GM(1，1)灰色模型．