道岔缓和曲线尖轨切削方式选型的动力学研究

曹 洋，王 平，黄 明

(1．福州大学土木工程学院，福建福州 350116;

2．西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031)

0 引言

道岔平面线型设计中尖轨切削方式选择得合适与否，将对行车性能和结构使用特性产生不同程度的影响［1］，目前已有关于直线型和圆曲线型尖轨切削方式选型的研究［2］，随着列车侧向过岔速度不断提高，缓圆缓型道岔逐渐出现，而针对前缓和曲线上尖轨切削类型的确定方法仅限于几何和静力手段，并不能准确反映车辆动力作用下道岔转辙器结构选取不同切削方式尖轨时的使用状态．国内外对道岔转辙器结构的研究包括平面参数计算［3］、力学特性分析［4］和轮轨接触关系的扩展应用［5］等．本文以轮轨系统动力学为基础，建立车辆－转辙器动力耦合模型，分析了42号缓圆缓型道岔转辙器部位选取五种不同切削方式尖轨时，列车侧逆向通过振动系统的动力响应及钢轨磨耗程度，为缓和曲线尖轨选型提供动力学指导．

1 道岔转辙器部位轮轨动力模型建立

为正确模拟列车通过道岔转辙器部位时振动系统的动力特性，需采用合适的方法建立轮轨动力模型，由于车辆可简化为多刚体空间体系，而转辙器属于多自由度非线性结构，因此分别建立上部车辆和下部转辙器子模型，通过轮轨相互作用关系将两子模型耦合为整体模型．

1．1 车辆多刚体空间模型

车辆作为整体模型的动力来源，要求子模型可反映其典型的结构特征，同时需保证振动在系统中的传递，本文采用文献［6］中的单列全车多刚体空间模型，将一个车体、两个转向架和四个轮对分别模拟为具有各自外形尺寸的刚体，各刚体质量集中于几何形心，转向架与轮对、车体与转向架间的一系和二系悬挂系统简化为弹簧阻尼原件．车辆子模型共31个自由度，其中车体和两转向架均包含横移、沉浮、点头、摇头和侧滚五个自由度，各轮对包含横移、沉浮、摇头和侧滚四个自由度．

1．2 转辙器有限元模型

转辙器部位零部件多，且尖轨为变截面钢轨，均增加了其非线性特性，为使子模型能够准确模拟结构在列车动荷载作用下的振动状态，采用具有普遍性的有限单元法建模，模型示意图如图1和图2所示．

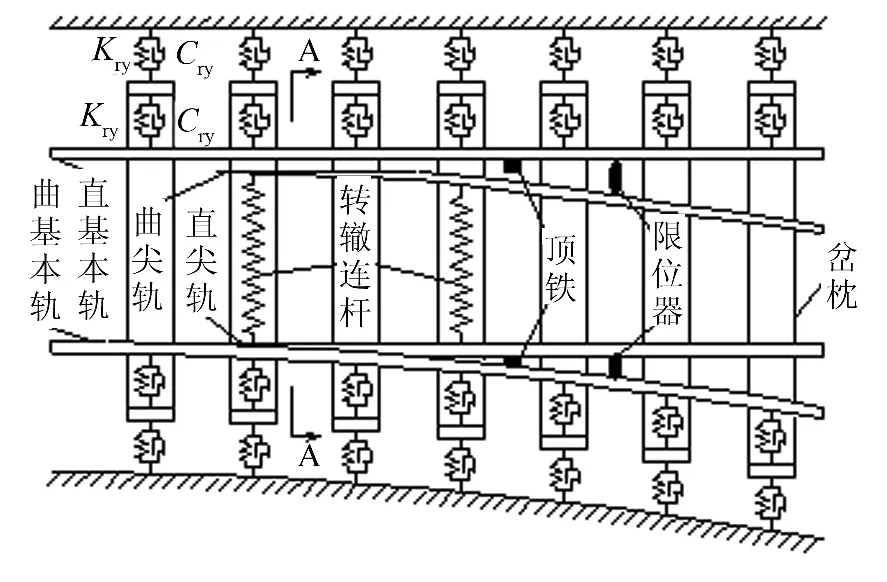
图1 转辙器子模型示意图Fig．1 Switch submodel

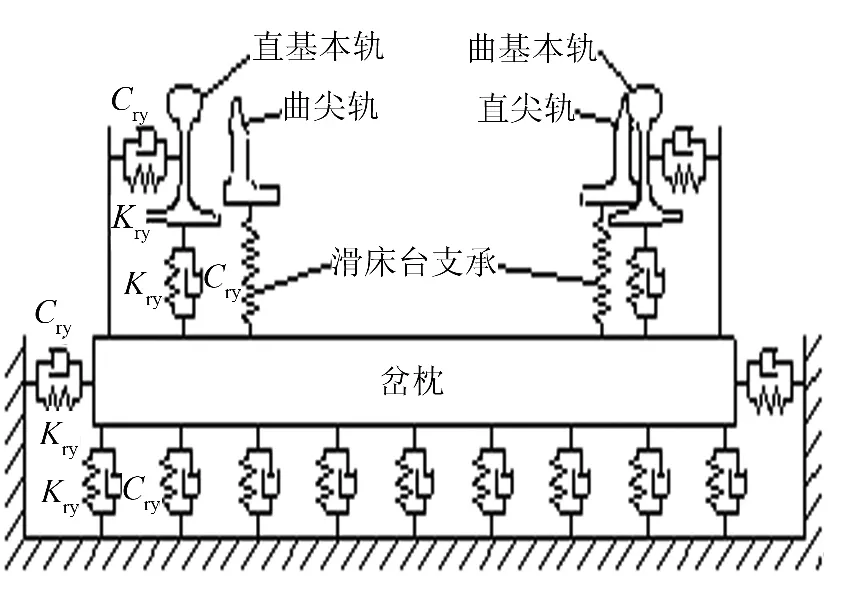
图2 转辙器子模型A－A断面图Fig．2 A －A section of switch submodel

图1转辙器子模型中各部位钢轨均模拟为双向弹性可弯欧拉梁，其中尖轨采用变截面梁代替，基本轨采用等截面梁代替，并以每根钢轨下部岔枕支承点为节点将其离散为有限单元，计算过程中考虑各单元的竖向和横向位移及转角．由于岔枕长度较长，横截面尺寸小，横向移动时仅存在整体质量块的位移，因此可将其视为竖向弹性可弯欧拉梁，同样在与钢轨的连接点处离散，考虑各单元竖向位移及转角．子模型中转辙连杆、顶铁和限位器等零部件均利用非线性弹簧表示，刚度根据具体设计值选取．

图2中子模型断面示意图显示其纵向为双层弹性点支承梁结构，尖轨前端下部滑床台为非线性支撑，仅承受压力，其余部位钢轨扣件及枕下基础模拟为弹簧阻尼原件，即图中Kr、Cr和Ks、Cs．

针对具有不同缓和曲线尖轨切削方式的转辙器建模时，依据各切削方式所得尖轨线型参数确定关键断面廓形，计算时通过关键断面间插值即可得到所需断面．列车各种过岔方式中以侧逆向进岔对尖轨的撞击及磨耗作用显著，因此转辙器子模型应以侧股为主，直股辅助受力．

1．3 子模型耦合及振动求解方法

车辆和转辙器子模型的耦合需区分竖向和横向分别进行，其中车轮与钢轨竖向接触可视为两椭球状弹性体相互作用，简化为非线性赫兹接触［7］，横向接触根据轮轨间作用点位置不同，影响因素也有所区别，需采用非线性蠕滑理论［8］满足耦合要求．基于此耦合方法将两子模型耦合成为车辆－转辙器整体模型，利用哈密尔顿原理［7］结合对号入座法则建立模型质量、刚度、阻尼矩阵及荷载列阵，从而得到振动方程组，通过程序编制平台编写程序语言迭代求解．

列车侧逆向进岔时，采用爱因斯磨耗指数［9］对各类型尖轨切削方式磨耗性能进行对比评判，其基于轮轨动力作用下接触斑内磨耗功的消耗情况，可反映接触点位置变化以及大蠕滑或轮轨撞击所产生的钢轨磨耗．

2 缓和曲线尖轨切削类型计算工况

缓和曲线尖轨多出现在大号码缓圆缓型道岔设计中，包括切线型、半切线型、割线型、半割线型和相离半切线型五种类型，将相似尖轨切削方式在同一示意图中表示，分别如图3至图5所示．

图3 切线及半切线型尖轨Fig．3 Tangent and semi－ tangent switch rail

图4 割线及半割线型尖轨Fig．4 Secant and semi－ secant switch rail

图5 相离半切线型尖轨Fig．5 Separate －semi－tangent switch rail

图3中，自尖轨轨头顶宽bq1处向其理论起点方向沿直股工作边选取100～300 mm长直线段，将此范围内尖轨工作边取直线，即可得到切线型尖轨，若自尖轨轨头顶宽bq2处做曲股切线至直股工作边，则得到半切线型尖轨，两者尖轨尖端角分别为θ01和θ02;图4中，将直股工作边下移，与曲股工作边相割f，去除前端曲股被割部位即为割线型尖轨，若自尖轨轨头顶宽bq4处做曲股切线至直股工作边，则得到半割线型尖轨，两者尖轨尖端角分别为θ03和θ04;图5中，上移直股工作边，与曲股相离为f，此时自尖轨轨头顶宽bq5处做曲股切线至直股工作边，可得到相离半切线型尖轨，其尖轨尖端角为θ05．

选取前缓和曲线起点半径Rl为10 km、圆曲线半径R0为5 km的42号缓圆缓型道岔转辙器部位，依照不同尖轨切削方式分别建立转辙器子模型，各尖轨切削初始值尽量基于同一标准设定，以提高计算结果可比性，五种尖轨切削方式对应主要参数如表1所示．基于以上尖轨切削方式所建立转辙器子模型通用计算参数如表2所示．

表1 各缓和曲线尖轨切削方式主要参数Tab．1 Main parameters of every cutting mode of switch blade

表2 转辙器子模型计算参数Tab．2 Switch submodel calculation parameters

由于计算过程中列车以160 km·h－1速度侧逆向通过42号道岔各工况转辙器，且对于尖轨磨耗性能随列车过岔速度的计算中行车速度不超过250 km·h－1，因此选用静轴重P0=140 kN的250 km·h－1速度级动车组，对应车辆子模型计算参数如表3所示．

表3 车辆子模型计算参数Tab．3 Vehicle submodel calculation parameters

3 各切削方式计算结果对比

不同缓和曲线尖轨切削方式下整体系统的动力特性需通过行车安全性、平稳性和结构稳定性等多方面反映，因此选用列车侧逆向进岔时的脱轨系数、减载率、轮轴横向力、车体振动加速度及钢轨磨耗指数评判各切削方式的优劣性．考虑到列车前方第一轮对外侧车轮行驶状态受曲尖轨结构不平顺影响显著，两者相互作用剧烈，分析过程中可选取其对应各动力响应指标．

3．1 动力性能指标变化规律

转辙器缓和曲线尖轨选用各切削方式时，列车第一轮对外侧车轮脱轨系数Dc和轮重减载率Rw与转辙器长度S的分布关系如图6和图7所示．

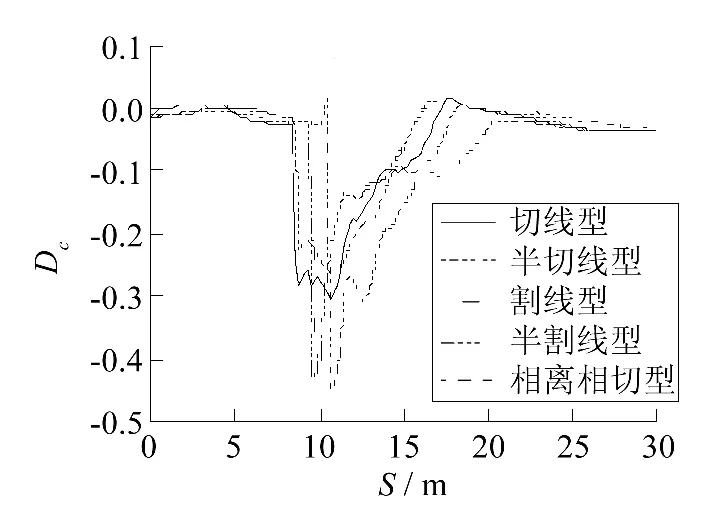
图6 车轮脱轨系数Fig．6 Derailment coefficient

图7 轮重减载率Fig．7 Deloading coefficient

图6中，各脱轨系数变化曲线在转辙器结构不平顺作用下波动明显，且外侧车轮撞击曲尖轨时导致横向力向负方向突变，使脱轨系数也对应发生变化，其中横向力以侧股内侧为正，由于各工况轮轨撞击位置不同，突变点有所差别，五种类型尖轨下车轮脱轨系数绝对值最大值分别为0．302、0．258、0．443、0．429 和 0．448，未超过安全限值 0．8［10］;图 7 中，轮重减载率同样受转辙器结构不平顺作用产生不同程度波动，而列车侧逆向进岔时的未被平衡离心力使外侧钢轨增载，减载率呈负值且逐渐减小，各尖轨切削方式下轮重减载率绝对值最大值分别为0．103、0．108、0．131、0．134 和 0．104，未超出安全限值0．6［10］．以上两安全性指标显示，缓和曲线尖轨选用半切线型切削方式效果较好，切线型次之．

图8 轮轴横向力Fig．8 Wheel axle lateral force

列车行驶于各类型缓和曲线尖轨转辙器部位过程中，第一轮对轮轴横向力F横向与转辙器长度S的分布关系如图8所示．

图8中，轮轴横向力在外侧车轮与曲尖轨撞击位置处有较大突变，且转辙器结构不平顺使其波动显著，由图可知轮轴横向力为负值，即方向指向侧股外侧，作用于曲尖轨无扣件扣压部位，有增加此处轨距的趋势，从而降低转辙器结构稳定性．五种切削方式下轮轴横向力绝对值最大值分别为16．770、14．336、23．735、24．356和23．906 kN，未超出动车组过岔时轮轴横向力限值计算式0．85(10+P0/3)［10］所得限值48．167 kN，同样以半切线型尖轨较优，切线型尖轨次之．

转辙器区车体垂向和横向振动加速度av和al与转辙器长度S的分布关系如图9和图10所示．

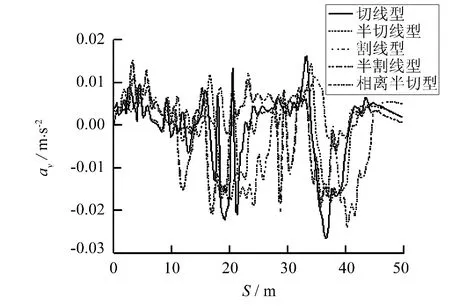
图9 车体垂向振动加速度Fig．9 Car body vertical acceleration

图10 车体横向振动加速度Fig．10 Car body lateral acceleration

由图9可知，车体垂向振动加速度在转辙器竖向结构不平顺作用下变幅较小，是由车辆一、二系悬挂对垂向振动的衰减所致，各类型尖轨对应其绝对值最大值分别为0．027、0．018、0．021、0．021和0．024 m·s－2，远小于垂向舒适度指标1．5 m·s－2［10］，对行车平稳性不起控制作用;图10中，车体横向振动加速度变化规律一致，受转辙器横向结构不平顺和车体未被平衡离心加速度影响，最大值分别为0．548、0．571、0．558、0．559 和 0．525 m·s－2，各数值差别较小，未超出横向舒适度指标 1 m·s－2［10］．

3．2 钢轨磨耗及影响因素分析

列车侧逆向进岔时，第一轮对外侧车轮对应钢轨磨耗情况W与转辙器长度S的分布关系，以及磨耗指数最大值Wmax随列车过岔速度v的变化分别如图11和图12所示．

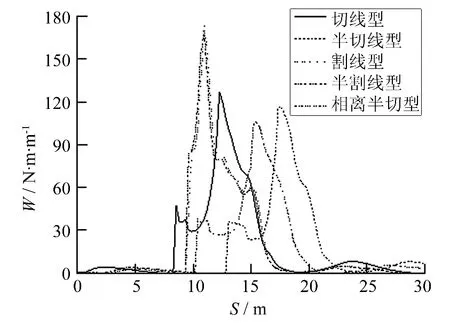
图11 外侧钢轨磨耗指数Fig．11 The outer rail wear index

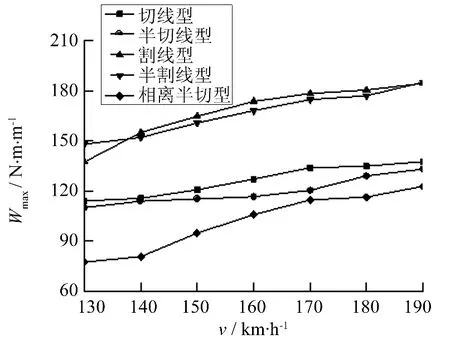
图12 磨耗指数最大值变化规律Fig．12 The maximum changing rule of wear index

从图11中可以看出，具有各种切削方式缓和曲线尖轨的转辙器部位，其外侧钢轨磨耗指数变化规律相似，即由于轮轨撞击作用使变化曲线在相应位置出现峰值，最大值分别达到127．190、116．655、173．696、168．224和105．839 N·m·m－1，因相离半切线型尖轨切削起点轨头宽度大，车轮进岔时与钢轨间撞击角度小，从而磨耗程度较小，半切线型和切线型尖轨次之．

图12中，列车分别以130～190 km·h－1速度侧逆向进岔时，各磨耗指数最大值均呈上升趋势，切线型、半切线型和相离半切线型尖轨对应磨耗指数最大值整体偏小，分别从 114．132、110．162和77．480 N·m·m－1增加至137．581、133．163 和122．848 N·m·m－1，其中采用半切线型尖轨时增长速度缓慢，切线型尖轨次之;割线型和半割线型尖轨下钢轨磨耗指数分别从137．421和148．135 N·m·m－1增加至184．494和185．146 N·m·m－1，增长速度较快．

3．3 各切削方式优劣性判断

综合以上各评判指标，对缓和曲线尖轨选用不同切削方式时的优劣性判断如表4所示．

表4 各缓和曲线尖轨切削方式性能比较Tab．4 Comparison of evaluation indexes of every cutting mode of switch blade

由表4可知，半切线型切削方式较适用于缓和曲线尖轨，也可根据转辙器各部件尺寸及配合设计等实际情况选择切线型方式，以满足具体使用要求．

4 结论

以轮轨系统动力学为基础建立了车辆－转辙器动力耦合模型，分别研究了缓和曲线尖轨采用不同切削方式对系统动力响应及钢轨磨耗的影响，为尖轨选型提供了动力学指导，所得结论如下:

1)从动力学角度对各缓和曲线尖轨切削方式优劣性加以评判，模拟所选取线型的实际使用状态，提高了尖轨选型的适用性和可靠性．

2)对于缓圆缓型道岔而言，前端缓和曲线尖轨选用半切线型切削方式时，对应行车性能、转辙器结构稳定性及钢轨磨耗程度综合达到最优，可在保证行车安全的前提下获得良好的平稳性，切线型尖轨次之，需根据实际情况确定设计方案．

3)运营中道岔均存在多种几何不平顺，对其转辙器部位动力特性模拟时，需将各种不平顺作用同时考虑，以增加计算结果的真实性．