一种基于连续损伤力学的低周疲劳寿命预测模型

一种基于连续损伤力学的低周疲劳寿命预测模型

陈凌张贤明欧阳平

重庆工商大学废油资源化技术与装备工程研究中心,重庆,400067

摘要：基于连续介质基本守恒定律和连续损伤力学,可将材料疲劳损伤造成的有效承载面积减小表示为平均应变的函数，在此基础上，按微裂纹阶段和疲劳裂纹阶段对材料低周疲劳的损伤演化进行了分析，并建立了一种低周疲劳寿命预测模型。对316L钢光滑试样进行420℃环境下应力控制的低周疲劳试验，采用上述方法进行损伤描述和寿命预测。结果表明微裂纹阶段是材料低周疲劳寿命消耗的主要阶段，采用各寿命段采样数据获得的寿命预测结果与试验结果较符合。

关键词：低周疲劳；损伤；平均应变；疲劳寿命;316L钢

中图分类号：O346.2；TG115.5

收稿日期：2014-12-12

基金项目：国家自然科学基金资助项目(51375516);重庆市应用技术开发重点资助项目(cstc2014yykfB90002);重庆工商大学科研启动经费资助项目(2014-56-10);教育部平台科技资助项目(fykf201502)

作者简介：陈凌，男，1979年生。重庆工商大学废油资源化技术与装备教育部工程研究中心博士、高级工程师。主要研究方向为金属材料的疲劳、断裂、腐蚀研究及机械结构安全评估。获发明专利授权9项,发表论文50余篇。张贤明,男,1955年生。重庆工商大学废油资源化技术与装备教育部工程研究中心主任、教授。欧阳平，男，1979年生。重庆工商大学废油资源化技术与装备教育部工程研究中心副研究员。

ALifePredictionModelforLowCycleFatigueBasedonContinuumDamageMechanics

ChenLingZhangXianmingOuyangPing

EngineeringResearchCenterforWasteOilRecoveryTechnologyandEquipment,

ChongqingTechnologyandBusinessUniversity,Chongqing,400067

Abstract:According to the basic conservation law of continuous media and continuum damage mechanics,the decrease of effective bearing area caused by the material fatigue damage could be expressed as a function of mean strain.The low cycle fatigue damage evolution of the micro crack stage and the fatigue crack stage were analyzed.And then,a model for the life prediction of low cycle fatigue was established.Through low cycle fatigue experiments with smooth specimens of 316L steel at 420℃ under stress control, the damage evolution were described and the fatigue life prediction was carried out by the method mentioned above.Results show that the micro crack stage is the main stage of low cycle fatigue life consumption of material.And compared with the experimental data, it is found that the predicted results which are obtained by the sampling data of different life periods are in good agreement with the experimental ones.

Keywords:lowcyclefatigue;damage;meanstrain;fatiguelife;316Lsteel

0引言

低周疲劳是石化、冶金、动力、航空航天等领域承压设备发生失效的主要原因之一,寿命预测是工程上进行安全评估的重要依据，长期以来受到国内外学者的关注[1-8]。这类模型主要是基于疲劳寿命与半寿命或循环稳定段的应变、应变能密度等参数之间的关系建立的，对疲劳进程的反映不够，对非稳定段的寿命预测精度不高。为更好地描述疲劳进程,国内外不少学者采用损伤力学对低周疲劳进行描述[9-14],选取合理、易测量的损伤变量反映损伤的进程是这类方法的关键所在。

针对上述情况,本文基于连续介质基本守恒定律和连续损伤力学(CDM),将材料疲劳损伤造成的有效承载面积的减小表示为平均应变的函数，并按微裂纹阶段和疲劳裂纹阶段对材料低周疲劳的损伤演化进行分析，在此基础上建立一种新的低周疲劳寿命预测模型。为验证上述方法的准确性,进行了316L钢光滑试样420℃环境下应力控制的低周疲劳试验，用本文所述方法进行了损伤演化的描述，同时采用本文所述寿命预测模型选取各寿命段采样数据进行了寿命预测。

1低周疲劳损伤演化及寿命预测

1.1连续介质基本守恒定律

金属材料为连续致密介质，满足连续介质普遍适用的基本守恒定律[15],即:在选定的连续介质集合内，某一物理量在物体体积上的物质积分的时间变化率，等于该物理量的分布源在该体积上的物质积分与物体表面流入的物理量的面积分之和。按此定义，连续介质的基本守恒定律可表示如下：

(1)

式中,Φ为某一给定的物理量;φ、ψ、π为同阶张量;V为物理量Φ占据的体积;∂V为V的表面;n为∂V的外法线矢量。

张量场函数的Green积分公式为

∫∂Vπ(n)ds=∫V(Σ·)dV

(2)

利用式(2),式(1)可改写为如下形式：

(3)

式中,Σ为比π高一阶的张量;为Hamilton算子。

输运定理的表达式为

(4)

式中，v为给定物理量通过∂v面的流出速度。

利用式(4),式(3)所示的守恒定律可改写为如下积分形式：

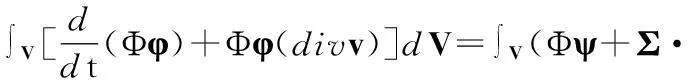
(5)

选取质量m为给定物理量代入式(5)，并取φ为1,ψ、Σ为0,式(5)可变形如下：

∫V(dm/dt+mdivv)dV=0

(6)

对于金属等不可压缩材料,divv=0,则由式(6)有dm/dt=0,即：

m0=mi

(7)

式中,m0为材料原始质量;mi为材料任一时刻的质量。

对于金属疲劳试样,由式(7)可得

ρΔlA=ρiΔliAi

(8)

式中,ρ为初始状态下试样材料密度;Δl为初始状态下选定的试样截面微元长度;A为初始状态下试样截面的有效承载面积;下标i表示任一时刻。

对于特定的温度环境,金属材料密度不变,式(8)可改写为

Δl/Δli=Ai/A

(9)

式(9)中,Δl与Δli可表示为如下关系式：

Δli=Δl+δli

(10)

式中,δli为相对于初始状态下试样截面微元长度的变化量。

将式(10)代入式(9),可得

Δl/Δli=1/(1+δli/Δl)=Ai/A

(11)

其中,δli/Δl的值即为应变ε,则式(11)可改写为

Ai/A=1/(1+ε)

(12)

式(12)表明金属疲劳试样有效承载面积的变化可表示为应变的函数。

1.2低周疲劳损伤演化

疲劳是在循环载荷下材料局部微结构发生不可恢复的损伤并累积的过程，根据CDM理论[15],低周疲劳的损伤演化包括微裂纹的形成、扩展和疲劳裂纹的形成、扩展及断裂。微裂纹通常在材料表面或亚表面形成及扩展，一旦形成疲劳裂纹后，将迅速发生扩展，引起材料断裂及失效。因此，低周疲劳的损伤演化具有明显的非均匀性，微裂纹阶段损伤变化缓慢，疲劳裂纹阶段损伤迅速增加，导致失效。在实际的工程应用中，通过对损伤的变化进行监测，即可知道损伤演化阶段，从而采取相应的防护措施。

根据CMD理论,材料内部微裂纹、微孔洞等微观缺陷产生、发展导致材料失效破坏的过程和规律，可通过引入损伤变量来描述和表征。对于单轴拉压疲劳试样，试样内部微裂纹、微孔洞等缺陷的产生和发展会造成试样有效承载面积减小，其损伤可定义为

D=1-A*/A

(13)

式中,A为试样初始状态下的有效承载面积;A*为试样产生损伤后的有效承载面积。

考虑到式(12),对于金属疲劳试样，应变的变化可用每一循环后的平均应变εm表征,则式(13)定义的损伤可改写为

D=1-1/(1+εm)

(14)

式(14)对循环周次N求导,可得损伤变化率：

vD=dD/dN=d[1-1/(1+εm)]/dN

(15)

在实际应用中,可用相邻采样周次的损伤变化计算式(15)的损伤变化率,如下所示:

VD,i=Δ[1-1/(1+εm)]i,i-1/ΔNi,i-1

(16)

式中,VD,i为第i采样周次的损伤变化率;Δ[1-1/(1+εm)]i,i-1为i和i-1采样周次间的1-1/(1+εm)差值;ΔNi,i-1为i和i-1采样周次间的循环周次。

通过损伤变化率可方便地区分低周疲劳损伤的演化阶段。损伤变化率变化平缓的阶段为微裂纹阶段，损伤变化率迅速增加的阶段为疲劳裂纹阶段。在实际监测过程中，一旦材料进入疲劳裂纹阶段，应采取相应防护措施或停车，防止设备发生失效。

1.3低周疲劳损伤及寿命预测模型

根据CDM理论,低周疲劳的损伤可选用合适的耗散势进行描述，并通过对耗散势积分得到损伤模型,材料常数通过试验进行确定和验证。前期研究[14]详细解释说明了疲劳损伤的基础理论，根据CDM理论,假定材料内部的损伤及能量耗散来自于塑性及微塑性变形，耗散势和损伤动力学定律可分别表示如下：

φ=φP+φD+φα

(17)

(18)

式中,φP为塑性耗散部分;φD为损伤耗散部分;φα为背应变耗散部分(极小,可忽略);λ为恒正的标量乘子;Y为应变能释放率。

选取合适的耗散势,代入式(18),积分后即可得到损伤模型。前期研究[15]已表明下式所示耗散势具有较好的代表性和适用性：

(19)

将式(19)代入式(18)可得

(20)

对式(20)进行积分，假定初始无损伤，积分上下限取为D|N=0=0，D|N=Nf=1，可得

D=1-(1-N/Nf)k

(21)

联立式(14)和式(21)可得

D=1-1/(1+εm)=1-(1-N/Nf)k

(22)

通过式(22)反算疲劳寿命，可得如下表达式：

Nf=N/[1-(1+εm)-1/k]

(23)

已知循环周次和对应周次的平均应变，利用式(23)即可得出材料的疲劳寿命,疲劳寿命与循环周次之差即为剩余寿命。相较于基于半寿命或循环稳定段疲劳参数的寿命预测模型，本模型对于各寿命段数据均可适用，尤其是疲劳前期和后期的非稳定段。另外，本模型为基于连续介质基本守恒定律和连续损伤力学推导得到的,理论依据明确，形式简单，可通过损伤变化率来反映材料的疲劳损伤进程，非常适合实际工程应用。

2试验结果及讨论

试验在岛津电液伺服疲劳试验机上进行,试验材料为316L钢棒材，热轧态，沿轴向方向取样，化学成分见表1。疲劳试样按国标GB/T15248-2008[16],采用螺纹夹持的圆棒试样。试验温度为420℃,控制方式为应力控制,应力比R=0,控制波形为正弦波,加载频率为3.5～5Hz。试验中采用高温引伸计自动记录应力和应变。试验温度下材料弹性模量为1.43×105MPa,屈服极限为241.9MPa,抗拉极限为512.4MPa。

表1　316L钢化学成分(质量分数)　%

表2为材料420℃下的低周疲劳试验数据,其中Δ σ为名义应力范围。加载过程中材料的平均应变 ε m为每次循环加载过程中的最小应变和最大应变的平均值。图1为材料420℃下平均应变 ε m随 N/ N f的变化图。图2为在图1所示的采样数据基础上,通过式(16)得到的材料420℃各低周疲劳载荷下损伤变化率随 N/ N f的变化图。

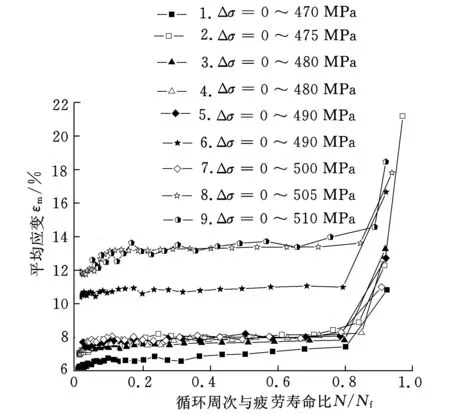
图1　316L钢420℃平均应变随N/N f变化图

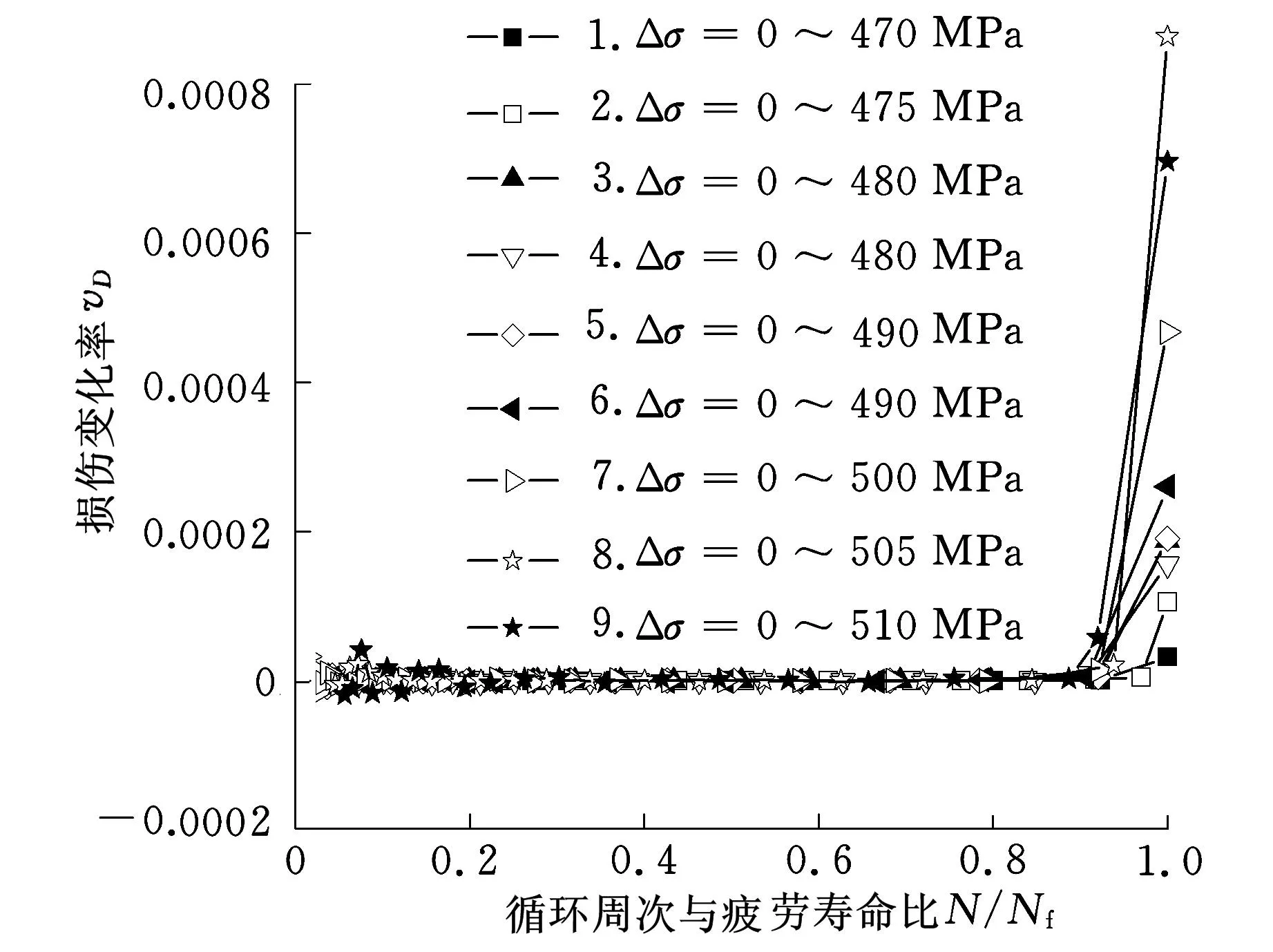
图2　316L钢420℃低周疲劳损伤变化率随N/N f变化图

以式(22)所示损伤表达式，以1-D(即1/(1+εm),剩余损伤)为纵轴,1-N/Nf(剩余寿命分数)为横轴,拟合可得316L钢420℃下各加载工况下的材料常数k,拟合图见图3,拟合结果列于表2。将k代入式(23)即可得316L钢中温低周疲劳的寿命预测表达式。

(a)1.Δσ=470MPa(b)2.Δσ=475MPa(c)3.Δσ=480MPa

(d)4.Δσ=480MPa (e)5.Δσ=490MPa(f)6.Δσ=400MPa

(g)7.Δσ=500MPa(h)8.Δσ=505MPa(i)9.Δσ=510MPa 图3　316L钢420℃低周疲劳损伤1-D与1-N/N f拟合关系图

如前所述,k为与载荷相关的材料常数,从表2可知,随加载名义应力范围的增加,k值逐渐增加。图4为材料常数k随加载名义应力范围Δσ的变化趋势。从图4可以看出,k随Δσ增加的变化呈线性关系，拟合曲线见图4，拟合关系为

k=-0.504 59+0.0012Δσ

(24)

相关度R=0.9516,将式(24)代入式(23)可得316L钢中温420℃下的低周疲劳寿命预测关系式如下：

Nf=N/[1-(1+εm)1/(0.504 59-0.0012Δσ)]

(25)

利用式(25),根据相应工作载荷下循环周次对应的平均应变，即可获得疲劳寿命。分别选取表2所述低周疲劳工况Nf/4、Nf/2、3Nf/4附近对应的循环周次和平均应变采样点,进行疲劳寿命的预测，预测效果见图5。

图4　材料常数k随名义应力范围变化拟合关系图

图5　316L钢420℃低周疲劳寿命预测效果图

从图5可以看出，本文提出的低周疲劳寿命预测模型对于材料各个寿命段的采样数据均具有较好的预测效果，所有的数据点均处于2倍误差带以内，其中Nf/2、3Nf/4对应的预测数据处于1.5倍误差带以内。

3结论

(1)基于连续介质基本守恒定律和连续损伤力学，材料疲劳损伤造成的有效承载面积的减少可表示为平均应变的函数D=1-1/(1+εm),用上述函数表征损伤，材料的损伤变化率可表示为

vD,i=Δ[1-1/(1+εm)]i,i-1/ΔNi,i-1

通过316L钢420℃下的低周疲劳试验,发现微裂纹阶段是材料低周疲劳寿命消耗的主要阶段(约90%),损伤变化率发展平缓,当形成疲劳裂纹后,损伤变化率迅速增加，材料快速失效。

(2)基于连续介质基本守恒定律和连续损伤力学，用平均应变的函数表示损伤，在此基础上,建立了一个新的低周疲劳寿命预测模型：

Nf=N/[1-(1+εm)-1/k]

该模型理论依据明确，形式简单,参数测量方便,适用于不同寿命段的寿命预测，非常适合实际工程应用。用上述模型进行了316L钢420℃下的低周疲劳寿命预测,对于不同寿命段的采样数据均具有较好的预测效果。

参考文献:

[1]Xia Z,Kujawski D,Ellyin F.Effect of Mean Stress and Ratcheting Stain on Fatigue Life of Steel[J].International Journal of Fatigue,1996,18(5):335-341.

[2]Humayun K S M, Tae-in Y. Evaluation of an Energy-based Fatigue Approach Considering Mean Stress Effects [J]. Journal of Mechanical Science and Technology, 2014, 28(4):1265-1275.

[3]Shukaev S, Gladskii M, Zakhovaiko A, et al. A Method for Low-cycle Fatigue Life Assessment of Metallic Materials under Multiaxial Loading [J]. Strength of Materials, 2008, 40(1):48-51.

[4]Ozaltun H, Shen M H H, George T, et al. An Energy Based Fatigue Life Prediction Framework for In-Service Structural Components [J]. Experimental Mechanics, 2011, 51(5):707-718.

[5]陈凌, 蒋家羚, 范志超, 等. 低周疲劳寿命预测的能量模型探讨[J].金属学报,2006,42(2):195-200.

Chen Ling, Jiang Jialing, Fan Zhichao, et al. Discussion of Energy Models for Low Cycle Fatigue Life Prediction [J]. Acta Metallurgica Sinica, 2006, 42(2):195-200.

[6]贾琦, 蔡力勋, 包陈. 考虑循环塑性修正的薄片材料低周疲劳试验方法[J]. 工程力学, 2014, 31(1):218-223.

Jia Qi, Cai Lixun, Bao Chen. A Testing Method to Investigate Low Cycle Fatigue Behavior of Slice Materials Based on Cycling Plasticity Correction [J]. Engineering Mechanics, 2014, 31(1):218-223.

[7]于慧臣, 董成利, 焦泽辉, 等. 一种TiAl合金的高温蠕变和疲劳行为及其寿命预测方法[J]. 金属学报, 2013, 49(11):1311-1317.

Yu Huichen, Dong Chengli, Jiao Zehui, et al. High Temperature Creep and Fatigue Behavior and Life Prediction Method of a Tial Alloy [J]. Acta Metallurgica Sinica, 2013, 49(11):1311-1317.

[8]胡绪腾, 宋迎东. 应用总应变-应变能区分法预测热机械疲劳寿命[J]. 燃气涡轮试验与研究, 2012,25(1):14-16,53.

Hu Xuteng, Song Yindong. Life Prediction for Thermomechanical Fatigue Using Total Strain Version of Strain Energy Partitioning[J].Gas Turbine Experiment and Research,2012,25(1):14-16,53.

[9]Herwig M. Fatigue Damage of Low Amplitude Cycles in Low Carbon Steel [J]. Journal of Materials Science, 2009, 44(18):4919-4929.

[10]Volkov I A, Korotkikh Y G, Tarasov I S, et al. Numerical Modeling of Elastoplastic Deformation and Damage Accumulation in Metals under Low-cycle Fatigue Conditions [J]. Strength of Materials, 2011, 43(4):471-485.

[11]Chen H, Shang D G, Tian Y J, et al. Comparison

of Multiaxial Fatigue Damage Models under Variable Amplitude Loading [J]. Journal of Mechanical Science and Technology, 2012, 26(11):3439-3446.

[12]张磊, 杨自春, 曹跃云. 一种新的低周疲劳损伤累积模型及试验验证[J]. 中国机械工程, 2011, 22(16):1912-1915.

Zhang Lei, Yang Zichun, Cao Yueyun. New Low Cycle Fatigue Damage Accumulation Model and Experimental Results [J]. China Mechanical Engineering, 2011, 22(16):1912-1915.

[13]郑战光, 蔡敢为, 李兆军, 等. 基于损伤力学阐释Manson-Coffin低周疲劳模型[J]. 中国机械工程, 2011, 22(7):812-814.

Zheng Zhanguang, Cai Ganwei, Li Zhaojun, et al. Interpretation of Manson-Coffin Model of Low Cycle Fatigue Based on Damage Mechanics [J]. China Mechanical Engineering, 2011, 22(7):812-814.

[14]陈凌,蒋家羚.一种新的低周疲劳损伤模型及实验验证[J].金属学报,2005,41(2):157-160.

Chen Ling, Jiang Jialing. A New Low Cycle Fatigue Damage Model and Its Experimental Verification[J].Acta Metallurgica Sinica,2005,41(2):157-160.

[15]沈为.损伤力学[M]. 武汉: 华中理工大学出版社, 1995.

[16]中国国家标准化管理委员会. GB/T 15248-2008 金属材料轴向等幅低循环疲劳试验方法[S].北京: 中国标准出版社, 2008.

(编辑袁兴玲)