级联式多电平无桥整流器的研究

王 聪，焦 健，王 畅，蒋向北，程 红

（中国矿业大学（北京）机电与信息工程学院，北京 100083）

引言

为了能够应用低耐压的功率开关器件完成高电压的能量转换，传统的功率单元级联式多电平功率变流器在整流输入端需要应用体积庞大接线复杂的工频移相变压器，从而导致变流器的整流级体积庞大、笨重、成本高、损耗严重[1-2]。这使其在许多工业场合的应用受到了限制。近年来，为了去掉庞大、笨重复杂的工频变压器，大功率级联全控型（IGBT）H桥电力电子整流器在大功率场合的应用得到广泛的关注和研究[3-5]，其显著的优点是：不需要庞大、笨重复杂的工频变压器，可以应用低耐压的电力电子开关器件完成高压大功率的功率双向变换，并可使整流器以较小的谐波在超前、滞后或单位功率因数等多种工况下运行。但该类整流器的主电路拓扑结构所需要的有源开关器件较多，主电路工作过程中的损耗较大，针对所有有源开关器件的控制电路以及控制方法的设计也很复杂。

在许多工业应用场合能量并不需要双向传递，对于这样的工业应用场合，针对全控H桥级联多电平拓扑中开关管多、驱动电路复杂等问题，本文提出了一种新型无桥模块化级联整流拓扑结构，此拓扑采用无桥整流结构作为级联的基本模块单元，以两无桥模块级联整流结构为例，讨论了其基本工作原理，建立并分析了其稳态数学模型，提出了适用于此种拓扑的新型控制策略，并通过仿真和实验验证了控制策略的可行性和正确性。

1 无桥级联整流器的基本工作原理分析

大功率级联全控型（IGBT）H桥电力电子整流器电路拓扑如图1所示。本文提出的无桥级联整流器是由多个无桥PFC结构级联而成，其电路拓扑如图2所示。在此模块单元中，减少了一半的开关管数量，简化了控制和驱动电路，降低了开关损耗，提高了系统效率。但这种结构存在弊端，即在功率因数角为零时，电感电流会不可避免地产生畸变，并且随着负载的增加畸变的程度也会增加，在对电感电流畸变原因深入分析的基础上，本文提出了新的控制方法。

图1 全控H桥结构级联整流器拓扑结构Fig.1 Full-controlled cascaded H-bridge rectifier topology

图2 无桥结构级联整流器拓扑结构Fig.2 Cascaded bridgeless rectifier topology

以两模块级联为例分析无桥级联整流器的工作原理，电路如图3所示。

图3 无桥结构级联整流器拓扑结构（两模块）Fig.3 Cascaded bridgeless rectifier topology（two modules）

当电感L的电流连续时，在输入电流正半周期，对于整流模块1，S1开通时，UCON1为0 V，记做0电平；S1关断时，UCON1为直流侧输出电压U1，记做1电平，S2的开关状态对UCON1无影响；同理对于整流模块2，当S3开通和关断时，UCON2分别为0 V（0电平）和直流侧输出电压U2（1电平），此时，S4的开关状态对UCON2无影响。这样在电感L电流正半周期，UCON就可以输出0 V、-1 V和2 V 3种电平；同理在电感L电流负半周期，通过对S2、S4的控制，UCON可以输出0 V、-1 V和-2 V 3种电平。通过在电流的正半周和负半周分别控制 S1、S3和S2、S4就可以控制UCON1、UCON2和UCON，从而按要求控制输入电流，与此同时还可以完成对直流侧电压U1和U2的均衡控制。下面通过对其工作过程的详细分析，进一步讨论无桥级联整流器的稳态数学模型。

1.1 系统稳态模型

由于在每个模块中，2个开关管可以同时开通和关断，因此图3中的4个开关管仅仅需要2种驱动信号来控制。在工作过程中，电路中的4个开关管（S1，S2，S3，S4）可以有 4 种工作状态，即：（1，1，0，0），（1，1，1，1，），（0，0，1，1），（0，0，0，0），其中“1”表示导通，“0”表示截止。 不失一般性，（（S1，S2），（S3，S4））的驱动脉冲如图 4 所示。 图 4 中：d1为开关管 S1、S2的导通占空比，d2为开关管 S3、S4的导通占空比，d3Ts为 S1、S2与 S3、S4驱动脉冲之间的时间间隔。

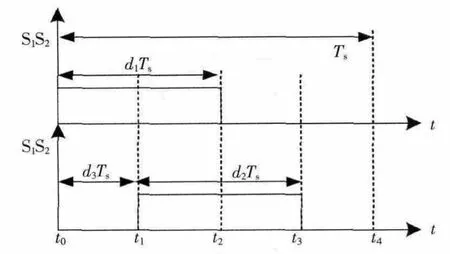
图4 开关管驱动脉冲Fig.4 Driving pulse of power switches

把一个开关周期分为4个时间段对电路进行分析，各时间段电路中电流流通路径如图5所示。

设定整流模块1和整流模块2直流侧电容C1=C2=C，由于电源电压正负半周对称，这里只对正半周工作情况进行分析，则有

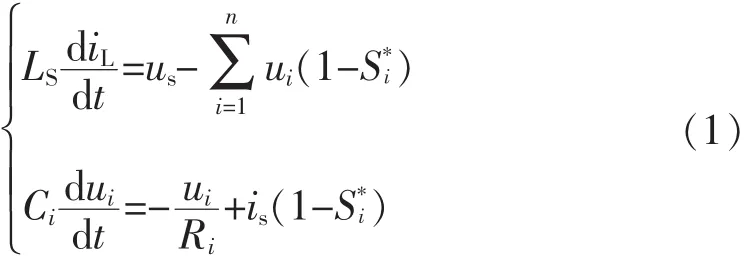
图5 各时间段电路中电流流通路径Fig.5 Current flow path at each interval

式中：us、iL分别为电网的电压和电流；LS为交流侧升压电感；Ci、Ri、ui分别为第 i个功率单元的直流母线电容、负载等效电阻、直流输出电压；S*i=1-Si，Si为开关管的开关状态 Si=0，1，i=1，2，…，n。

解式（1）可得关于每个模块直流输出电压与输入电压以及电感电流与输入电压之间的稳态模型，其模型表达式为

由式（2）可以看出，通过控制占空比d1和d2可以控制两个模块的输出电压u1、u2及电感电流iL。

1.2 功率因数分析

全控H桥级联整流器，通过控制整流器交流侧端电压，就可以控制输入电流的幅值和相位，从而使整流器可以在任意功率因数下运行。与全控H桥级联整流器不同，无桥整流器无论是单个模块还是级联结构本质上都无法满足单位功率因数要求，而且功率因数会随着直流侧负载的加重而降低。下面以单模块无桥整流器为例对此进行说明。

单模块无桥整流器电路拓扑、相量和相位关系示意如图6所示。图6（a）为单模块无桥整流器电路图，图6（b）为满足单位功率因数情况下图 6（a）所示电路的相量图，图6（c）为按此向量图得出的无桥电路交流侧电压UCON和电感电流IL的相位关系图。由图6可知：若要使电感电流IL与电源电压US同相位，则控制电压UCON必须滞后电感电流IL一个角度θ，按此相位关系分析无桥结构电路图可知，在电感电流过零点开始的θ范围内，电感电流IL和控制电压UCON应具有相反的方向。而由前面的分析可知，在无桥结构中，当电感电流IL方向为正方向时，UCON只能输出0，1两种电平，无法输出负值，因此在这一阶段UCON只能输出零电平。

当UCON为0时，可得出iL为

由以上两式可以得出，在此阶段，电感电流iL不再和电源电压Us同相位，而是突然滞后于Us90°。但由于电感电流不能突变，因此在这一阶段电感电流将呈缓慢上升的趋势。

图6 单个无桥整流电路拓扑、相量图及相位关系Fig.6 Circuit typology，phasor diagram and phase relationships of bridgeless rectifier

因此按图6（b）相量图结构进行控制，在电感电流过零点附近，输入电流波形将不可避免地发生畸变，并且随着电感电流的增加（负载的加重）畸变会变得越来越严重。

新的控制策略要求电感电流滞后于电源电压一个角度，且滞后的角度与负载大小有关。非单位功率因数时电路相量及相位关系如图7所示。由图7的几何关系可得出功率因数角和负载的关系为

图7 非单位功率因数时电路相量及相位关系Fig.7 Cirauit phasor and phase relationships in Non-unity power factor

1.3 系统控制策略

按照本文前面所讨论的方法，控制器应能够随着负载的变化调整输入电流滞后于电源电压的相位，使输入电流始终保持与整流器输入电压同相位，同时通过对开关器件导通占空比的调节，使级联的模块输出直流电压达到均衡。

传统基于乘法器的PID控制策略如图8所示，控制策略采用双闭环控制，电压环的PI调节器输出值乘以电源电压的瞬时值作为电流环的给定值，使电感电流与输入电压同相位[6-8]，势必会使电感电流在过零点附近产生一定程度的畸变。加入滞后角控制后的控制框图如图9所示。图9中的电压电流双环控制使电感电流给定滞后于输入电压，滞后角φ可由式（5）计算出。

如前所述，各级联模块输出电容电压平衡是级联结构整流器能够应用低耐压的功率开关管完成高电压的功率转换的关键。在文中所讨论的级联无桥整流器中，各个模块流过的电流相同，但是由于级联模块的负载不同，所以级联模块负载两端的电压也不同。

图8 不考虑滞后角的双闭环控制结构Fig.8 Traditional double-loop control structure without lagging angle

图9 加入滞后角的双闭环控制结构Fig.9 Double-loop control structure with lagging angle

2 仿真分析

本文应用PSIM软件对以上两种控制策略进行了仿真分析，仿真电路参数如表1所示。

表1 级联式整流拓扑变换器仿真参数Tab.1 Simulation parameters of AC－DC converter

在不采用加滞后角的控制策略情况下，电感电流在过零点处会产生严重的畸变，其电流波形如图10所示；而采用加滞后角的控制策略后，电感电流的相位滞后于电源电压相位，但其波形接近于正弦波，如图11所示。通过仿真验证了新型拓扑的可行性和控制策略的正确性。

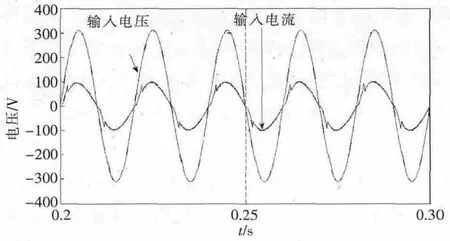
图10 传统控制方式的电感电流和输入电压波形Fig.10 Inductor current and input voltage waveforms in traditional control mode

图11 加入滞后角控制时电感电流和输入电压波形Fig.11 Inductor current and input voltage waveforms with lagging angle control mode

图12 两种控制方式下电流THD变化趋势对比Fig.12 Current THD changing trend comparison in two control modes

图12 和图13分别给出了采用传统控制方法和新控制方法时电流THD随负载的变化以及功率因数随负载的变化，由图12可看出，随着负载的加重，传统控制方法的电流THD会显著增加，而采用新控制方法后的电流THD会一直保持较低的水平；由图13可以看出，在某一段负载范围内新控制方法的功率因数会略低于传统控制方法，但当负载很重时，新控制方法下的功率因数会远高于传统控制方法的功率因数。

图13 两种控制方式下功率因数变化趋势对比Fig.13 Trend comparison of power factor in two kinds of control modes

3 实验验证

为了验证新型的级联式整流电路拓扑的正确性以及仿真的正确性，本文搭建功率为1 kW的实验平台。实验平台参数如表2所示。

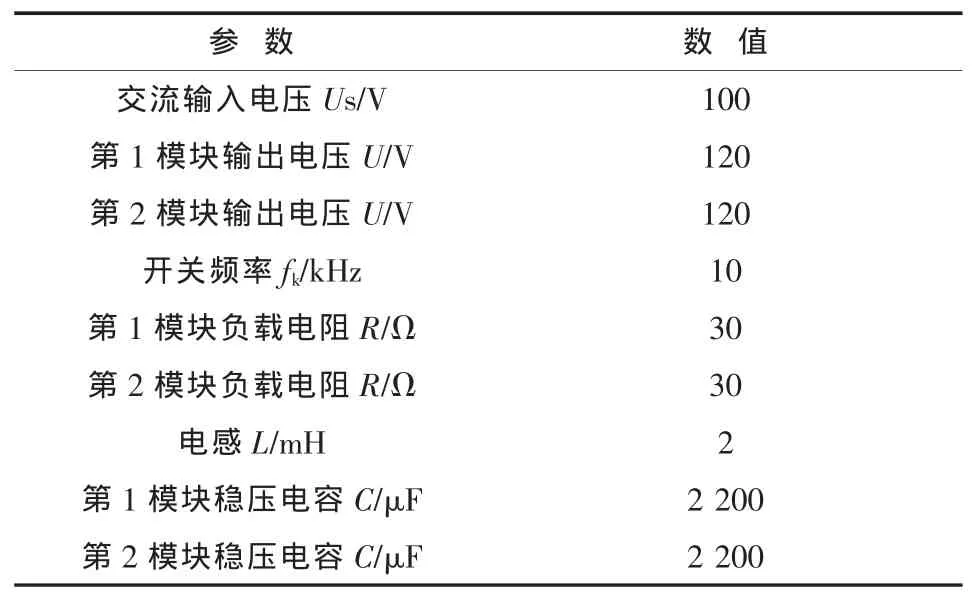
表2 级联式整流拓扑变换器参数Tab.2 Parameters of AC－DC converter

图14 为实验装置在输入100 V交流电，每个模块输出电压120 V情况下，采用传统控制方式时输入电压和输入电流的波形图，由图可知：输入电压和输入电流基本同相位，但电流已经发生了一定程度的畸变。由图15中FFT分析可以看出，3次谐波和5次谐波所占比例都很大。

图16 为采用滞后角控制策略后的电源输入电压和电感电流波形，由图可知：电感电流波形接近正弦。图17为电感电流波形的FFT分析，可以看出，谐波较之前有大幅度的改善。

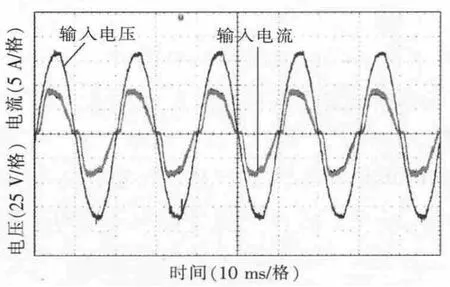
图14 传统控制方法的电感电流波形Fig.14 Inductor current waveforms in traditional control method

图15 传统控制方法电感电流的FFT分析Fig.15 FFT analysis of inductor current in traditional control method

图16 加入滞后角控制方法的电感电流和输入电压波形Fig.16 Inductor current and supply voltage waveforms in lagging angle control method

图17 移相控制方法的电感电流FFT分析Fig.17 FFT analysis of inductor current in lagging angle control method

4 结语

针对全桥级联整流结构开关管多、成本高、控制和驱动电路复杂的缺点提出了新型无桥级联拓扑结构，并建立了其稳态数学模型。在对传统基于乘法器的单位功率因数控制方法存在电感电流过零点畸变的问题进行详细分析和论述的基础上提出了适用于无桥级联结构的控制策略，即在传统控制策略中加入电流滞后角控制环节，使电感电流滞后于电源电压，从而达到消除电感电流过零点畸变的问题，同时保持系统具有较高的功率因数。论文给出了电流滞后角与负载关系的数学表达式，给出了在负载变化范围内，满足功率因数要求的电感选择原则，给出了使各级联模块输出电压保持均衡的控制策略。最后通过仿真和实验平台验证了控制策略的正确性。改进后的控制策略使电感电流波形接近正弦，同时在整个负载变化范围内功率因数大于0.9。

[1]Li Zixin，Wang Ping，Chu Zunfang.An improved pulse width modulation method for chopper cell based modular multilevel converters[J].IEEE Transactions on Power Electronics，2012，27（8）：3472-3481.

[2]Sankala A，Korhonen J，Strom J，et al.Modular Double-Cascade Converter[C].Applied Power Electronics Conference and Exposition，2012，21（2）：647-652.

[3]Clare J.Advanced power converters for universal and flexible power management in future electricity networks[C].in Proc.13th EPE，2009，36（2）：1-29.

[4]Xu She，Wang Fei，Burgos R，et al.Solid state transformer interfaced wind energy system with integrated active power transfer，reactive power compensation and voltage conversion functions[C].Energy Conversion Congress and Exposition（ECCE），2012，22（6）：3140-3147.

[5]Akagi H，Inoue S.Medium-Voltage Power Conversion Systems in the Next Generation[C].Power Electronics and Motion Control Conference，2006（1）：1-8.

[6]Li Yong，Toshio Takahashi.A Digitally Controlled 4-kW Single-Phase Bridgeless PFC Circuit for Air Conditioner Motor Drive Applications[C].Power Electronics and Motion Control Conference，2006，45：1-5.

[7]Cho Younghoon，Lai Jihsheng.Digital Plug-In Repetitive Controller for Single-Phase Bridgeless PFC Converters[J].IEEE Transactions on Power Electronics，2013，28 （1）：165-175.

[8]Chen Hungchi，Chung Chaochiang.Input Current Control for Bridgeless PFC Converter without Sensing Current[C].Applied Power Elec tronics Conference and Exposition（APEC），2014，25：1821-1826.