基于开关耦合电感单元的Z源逆变器

刘方荣，荣 飞

（湖南大学电气与信息工程学院，长沙410082）

引言

传统逆变器中电压型逆变器只能降压，电流型逆变器只能升压,而由电磁干扰引起的直通和开路控制信号分别对电压型逆变器和电流型逆变器构成严重威胁。近年来，Z源逆变器由于克服了上述缺点，成为了研究的热点。目前，对Z源逆变器的研究主要包括：调制策略的研究、拓扑结构的研究、Z源逆变器的建模与控制以及Z源逆变器的应用。其中Z源逆变器在拓扑结构方面主要包括：传统的Z源逆变器[1]、Quasi-Z 源逆变器[2]、Semi-Z 源逆变器[3]、Trans-Z 源逆变器[4]和开关电感 Z 源逆变器[5]。 在提高Z源逆变器电压增益能力方面采取的主要手段有：采用改进的调制策略，如采用最大增益控制方法或三次谐波注入控制策略[6-7]；采用变压器或开关电感改进拓扑结构，如采用Trans-Z源逆变器、开关电感Z源逆变器等；采用级联的方式，如级联的Quasi-Z 源逆变器[8]、级联的 Trans-Z 源逆变器[9]等。

本文引入了近年来DC/DC变换器中所使用的开关耦合电感单元[10-11]，并以此改进Z源逆变器拓扑结构，从而使Z源逆变器获得更高的电压增益。

1 拓扑结构

近年来，在DC-DC变换电路中，一种简单有效的提高电压增益的方式就是在电路中引入开关耦合电感单元。开关耦合电感单元由一个耦合电感和一个二极管（或其他开关器件）组成，其中耦合电感的一次侧绕组取代变换电路中的一个电感，耦合电感的二次侧绕组和二极管组成的串联支路与DCDC变换电路中原有的二极管并联。这就使得在实际运行中，耦合电感在开关器件关断时漏感能量能够通过原有的并联二极管传输到负载上，从而实现开关耦合电感的软开关功能。如果只考虑理想的开关耦合电感单元，忽略漏感的影响，则原有的并联二极管支路可以去掉[10-11]。

本文基于理想的开关耦合电感单元，分析了开关耦合电感对Z源逆变器电压增益的影响，并在常见Z源逆变器拓扑结构基础上对应提出了一系列基于开关耦合电感单元的Z源逆变器。

传统的Z源逆变器和Quasi-Z源逆变器引入开关耦合电感单元后的拓扑结构如图1所示。图中开关耦合电感单元的一次侧绕组取代Z源逆变器中的电感，开关耦合电感单元的二次侧绕组与二极管组成的串联支路取代Z源逆变器中的原有二极管。n为一二次侧绕组间的电压变比。

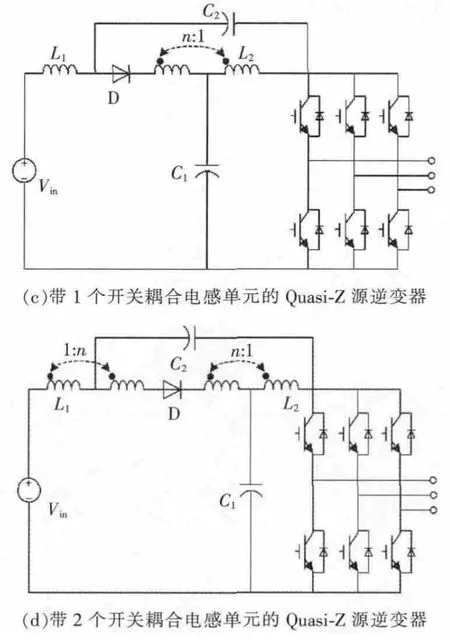
图1 基于开关耦合电感单元的Z源逆变器拓扑结构Fig.1 Topologies of switched coupled inductor Z-source inverters

为了便于下文引用，本文将传统的Z源逆变器用Z表示，传统Quasi-Z源逆变器用QZ表示。将图1中带1个开关耦合电感单元的Z源逆变器用SCI1-Z表示，带2个开关耦合电感单元的Z源逆变器用SCI2-Z表示，带1个开关耦合电感单元的Quasi-Z源逆变器用SCI1-QZ表示，带2个开关耦合电感单元的Quasi-Z源逆变器用SCI2-QZ表示。

2 带2个开关耦合电感单元的Z源逆变器原理分析

本文以图1（b）中SCI2-Z拓扑结构为例分析其工作原理。由于开关耦合电感单元的作用，耦合电感一次侧绕组上的电压通过电磁耦合作用，使得耦合电感二次侧绕组两端也存在电压，并且大小为一次侧绕组电压的n倍。在直通和非直通状态下的等效电路如图2所示。

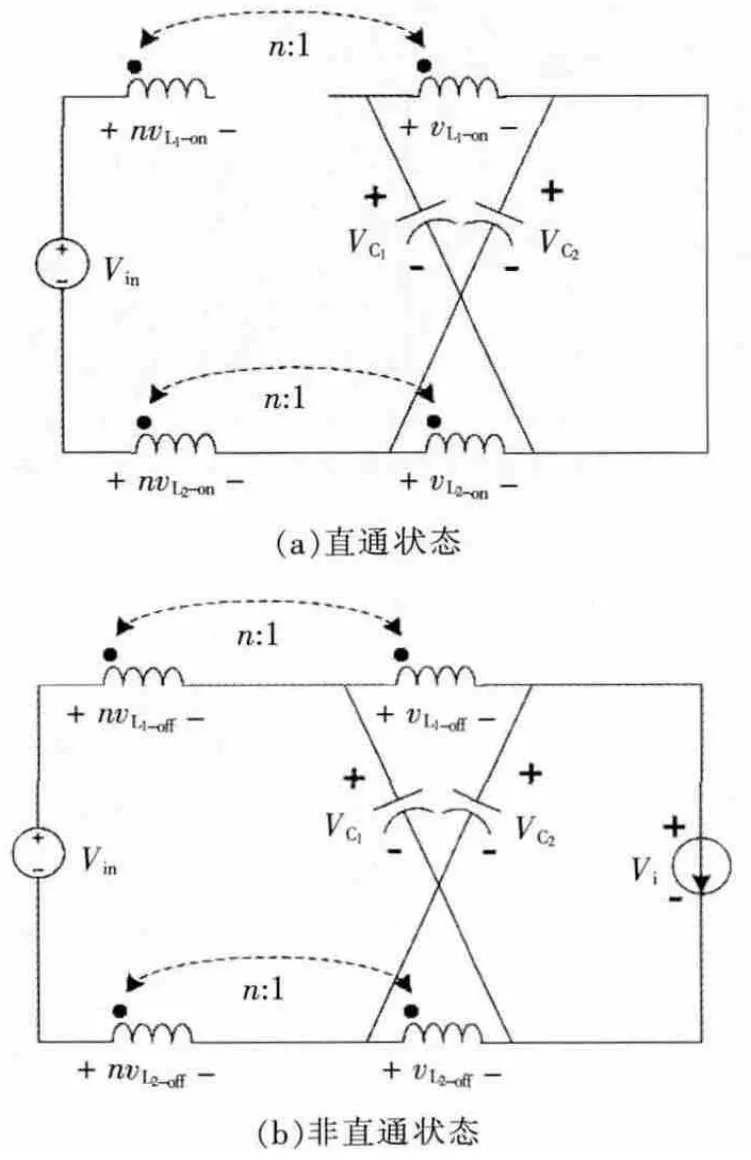
图2 SCI2-Z等效电路Fig.2 Equivalent circuits of SCI2-Z

在直通状态下，二极管D反向阻断。电容C1和C2放电，2个耦合电感充电。根据基尔霍夫电压定律，有

式中：vL1-on为直通状态时第1个耦合电感一次侧绕组上的电压；vL2-on为直通状态时第2个耦合电感一次侧绕组上的电压；VC1和VC2分别为电容C1和C2上的电压。

在非直通状态下，二极管D导通。电容C1和C2充电，2个耦合电感放电。根据基尔霍夫电压定律，有

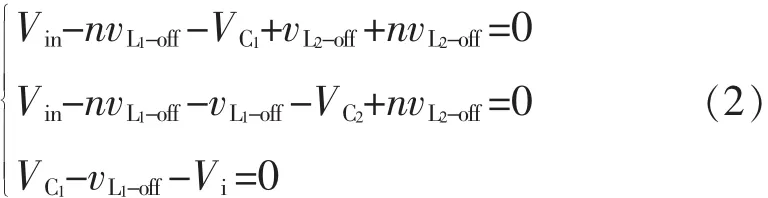
式中：vL1-off为非直通状态时第1个耦合电感一次侧绕组上的电压；vL2-off为非直通状态时第2个耦合电感一次侧绕组上的电压。式（2）经过推导可得

根据电感伏秒特性平衡原理，可知耦合电感一次侧绕组上的电压在一个开关周期内的平均值必须为0。因此

式中：D0为直通占空比；Ts为开关周期。

联立式 （1）、式（3）和式（4），可求得电容 C1和C2上的电压VC1和VC2，以及非直通状态下直流母线上的电压值Vi，即

因此，升压因子B可表示为

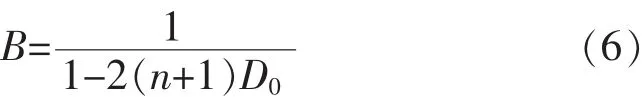
如果采用简单升压控制方式，则最大电压增益为

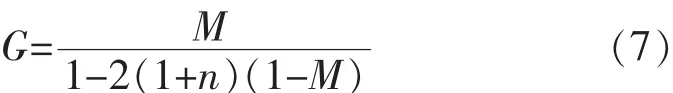
式中，M为调制度。

最大开关电压应力可表示为

根据式子（7）可得最大电压增益曲线，如图3所示。根据式子（8）可得最大开关电压应力曲线，如图4所示。

图3 最大电压增益曲线Fig.3 Curves of the maximum voltage gain

图4 最大开关电压应力曲线Fig.4 Curves of the maximum switch voltage stress

由图3和图4可以看出，当n=0时，耦合电感可看成普通电感，此时相当于传统Z源逆变器；当n≠0，即加入开关耦合电感单元时，Z源逆变器的升压能力得到提高，电压应力减小，并且n越大，Z源逆变器升压能力越强，电压应力也就越小。

由于Z源逆变器的升压特性，图1中4种拓扑结构下的VC1大于电源电压Vin。在直通状态时，Z源电容对耦合电感放电，因为VC1大于Vin，所以二极管D受反压关断；在非直通状态时，耦合电感和电源Vin共同对Z源电容和负载放电，因为耦合电感感应电压的作用，所以二极管D正向导通。由于图1中4种拓扑结构具有相同的充放电特性，因此对拓扑结构SCI2-Z的原理分析可以推广到图1中其他的拓扑结构。类似于SCI2-Z的分析，可以计算出图1中其他拓扑结构下的升压因子B以及Z源网络电容上的电压 VC1、VC2与输入电压 Vin的比值。将这些改进拓扑结构下的数据与传统的拓扑结构Z和QZ的数据进行对比，结果如表1所示。由表1可知：①传统拓扑结构Z、QZ在利用开关耦合电感单元取代原有电感之后升压因子B以及VC1/Vin、VC1/Vin更大；②采用2个开关耦合电感单元时的B以及VC1/Vin、VC2/Vin比采用1个开关耦合电感单元时更大；③耦合电感的电压变比n越大，B的值越大，升压能力越强。因此，本文提出的基于开关耦合电感单元的Z源逆变器电压增益能力更强，并且引入的开关耦合电感单元个数越多，耦合电感电压一二次侧电压变比n越大，电压增益能力越强，电容电压应力也会越大。

表1 所有拓扑结构的升压因子和电容电压Tab.1 Booster factor and capacitance voltage of all topology structure

3 仿真与实验

本文以拓扑结构SCI2-Z为例，进行仿真与实验。直流电源电压Vin取50 V，Z源电容C1、C2取1 000 μF，2个开关耦合电感单元相同，耦合电感励磁电感值为210 μH，漏感值约100 nH，电压变比为n。三相逆变器输出侧滤波电感取2 mH，滤波电容取 100 μF、负载电阻为 10 Ω。 调制度取 0.75，直通占空比取0.1，开关频率取10 kHz。采用简单升压控制方法。当n分别取1、2、3时的仿真结果如图5所示。 图中VC1、Vi、Vload分别为Z源电容 C1上的电压、直流母线电压和负载相电压。从图中可以看到，当n=1时，VC1为75 V，Vi为 83 V，负载相电压 Vload的峰值为31 V；当n=2时，VC1为 112 V，Vi为 125 V，负载相电压Vload的峰值为47 V；当n=3时，VC1为223 V，Vi为250 V，负载相电压Vload的峰值为93 V。仿真结果与表1中公式计算所得结果相符，验证了本文的理论分析。

为了进一步验证本文理论分析的正确性，根据上面的仿真参数搭建了Z源逆变器实验平台。在实验中开关耦合电感单元的电压变比n为2。利用电阻分压的方法检测输入电压Vin、Z源电容电压VC1和直流母线电压Vi，利用电压互感器检测负载相电压Vload。图6为输入电压Vin和Z源电容电压VC1的实验波形。从图中可以看出，输入直流电压为50 V，Z源电容电压约为110 V。图7为直流母线电压波形。从图中可以看出，直流母线电压约为125 V。图8为负载相电压波形。从图可以看出，负载相电压峰值大小约为45 V。实验结果与理论分析相符。

图5 SCI2-Z在n取不同值时的仿真波形Fig.5 Simulation results of SCI2-Z for different n

图6 直流输入电压和Z源电容电压波形Fig.6 Voltage waveforms of DC input and Z-source capacitor

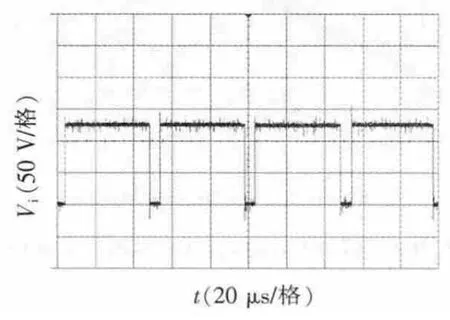
图7 直流母线电压波形Fig.7 DC-link voltage waveform

图8 负载相电压波形Fig.8 Phase voltage waveform of load

4 结语

本文设计了一种开关耦合电感单元，并将它引入到Z源逆变器当中，提出了一系列基于开关耦合电感单元的Z源逆变器拓扑结构。通过理论分析和公式推导，得到Z源逆变器的升压因子以及电容电压应力。用开关耦合电感单元取代传统的Z源逆变器拓扑结构中的电感可以有效地提高Z源逆变器的电压增益，且开关耦合电感单元的个数越多，电压变比越大，Z源逆变器的电压增益能力越强，电压应力越小。本文以带2个开关耦合电感单元的Z源逆变器为例进行了仿真和实验。实验结果与理论推导的结果一致。本文所提出的基于开关耦合电感单元的Z源逆变器相较传统的几种Z源逆变器拓扑结构在电压增益和电压应力方面具有明显的优势，对于光伏发电、风力发电等输入电压小、电压增益要求高的场合具有广泛的应用价值。

[1]Peng Fangzheng.Z-Source Inverter[J].IEEE Transactions on Industry Application.2003，39（2）：504-510.

[2]Joel Anderson,Peng Fangzheng.Four Quasi-Z-Source Inverters[C].Power Electronic Specialists Conference.Rhodes，2008： 27843-2749.

[3]Cao Dong,Jiang Shuai,Yu Xianhao,et al.Low Cost Single-Phase Semi-Z-source Inveters[C].Applied Power Electronics Conference and Exposition.Fort Worth， USA：IEEE，2011：429-436.

[4]Qian Wei， Peng Fangzheng， Cha Honnyong.Trans-ZSource Inverters[J].IEEE Transactions on Power Electronics.2011，26（12）：3453-3463.

[5]Zhu Miao,Yu Kun,Luo Fanglin.Switched Inductor ZSource Inverter[J].IEEE Transactions on Power Electronics.2010，25（8）：2150-2158.

[6]房绪鹏.Z源逆变器研究[D].杭州：浙江大学,2005：61-65 Fang Xupeng.Research on Z-Source Inverter[D].Hang zhou：Zhejiang University，2005：61-65（in Chinese）.

[7]张超华，汤雨，谢少军.改进Z源逆变器的三次谐波注入控制策略[J].电工技术学报，2009，24（11）：114-119.Zhang Chaohua,Tang Yu,Xie Shaojun.Third Harmonic Injection Control Strategy of Improved Z-Source Inverter[J].Transactions of China Electrotechnical Society，2009，24（11）：114-119（in Chinese）.

[8]Dmitri V，Indrek R,Ryszard S，et al.Step-Up DC/DC Converters With Cascaded Quasi-Z-Source Network[J].IEEE Transactions on Industrial Electronics.2012， 59（10）：3727-3736.

[9]Li Ding,Poh Chiang Loh,Zhu Miao,et al.Cascaded Multicell Trans-Z-Source Inverters[J].IEEE Transactions on Power Electronics,2013，28（2）：826-836.

[10]Berkovich Y,Axelrod B.Switched-Coupled Inductor cell for DC-DC Converters with very large conversion ratio[C].IET Power Electronics，2011，4（3）：309-315.

[11]Chen ShihMing,Liang TsorngJuu,Chen Kaihui,et al.A Novel Switched-Coupled-Inductor DC-DC Step-Up Converter[C].Energy Conversion Congress and Exposition.Denver，2013：1830-1833.