高中数学教材的二次开发

王忠

摘 要 高中数学教材的二次开发是教师在原有教材的基础上对课本内容进行更深一层的挖掘，对教材进行补充扩展。高中数学教材的二次开发有助于学生对知识更深一步的了解，本文主要从问题情境的创设、知识概念、数学公式以及例题四个方面分析了高中数学教材二次开发的方法。

关键词 高中数学 教材 二次开发

教材是教师进行教学的重要资源，高中数学教材，为教师教学提供了一个参考。但是由于教材本身的限制，一些问题在教材中并没有深入地讲解，所以教材二次开发就显得非常的重要。教材的二次开发，主要就是教师在原有教材的基础上，针对书中的某些概念、公式、习题等进行一些知识的扩展补充。高中数学教材的二次开发，我们主要从以下几个方面进行分析。

一、问题情境创设的开发

好的开场是一节课成功的一半，由于数学本身是比较枯燥抽象的，教师在进行教学的时候如果只是单纯地复述课本的内容，不仅不能很好地传递知识，也不能激发学生的学习兴趣。情境创设是学习过程中非常重要的一个环节，创设适当的问题情境，通过生活的实例引入课堂内容，既可以提高学生学习的兴趣，增加学生学习的欲望，也可以将抽象的知识变得具体化。

例如，在高中数学教材选修《圆锥曲线》一章中，教师就可以创设恰当的问题情境。在《椭圆》一节中，教师可以让同学们举一些生活中见到的椭圆形的物体，如放映机上的反射镜、汽车储油罐的轮廓、碎石机等实例[1]，通过这些实际生活中的物品，学生感受到椭圆的广泛应用。在《抛物线》一节中，教师可以用多媒体或者实物进行演示，还可以让同学们举一些生活中的例子，如喷泉中的水喷出的轨迹，依据生活中的具体事例，增加感性认识。

二、知识概念的开发

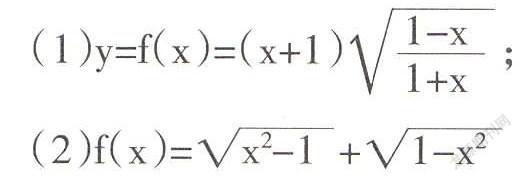
数学概念是高中数学教材的重要组成部分，概念是整个知识的基础，是数学知识拓展、运用的前提，数学概念在整个数学体系中占有非常重要的地位。但是在实际教学过程中，数学概念的教学却不是那么理想，其主要原因有以下几点：第一，对于数学概念的背景，没有做完整的介绍[2]；第二，对概念的发生以及后续发展历程没有足够的重视；第三，忽视对概念的总结与提炼。因此，在数学教学中，要加强对教材概念的开发。

例如，在高中数学必修教材《函数的奇偶性》一节中，教材中对于奇偶性的定义如下：一般的，设函数y=f（x）的定义域为A，如果对于任意的x∈A，都有f（-x）=f（x），那么称y=f（x）是偶函数；如果对于任意的x∈A，都有f（-x）=-f（x），那么称函数为奇函数。一般对于此类的概念，教师都是让学生自学或者是根据几个具体的函数画出图像来总结奇函数与偶函数的概念[3]。实际上教师可以对这个概念加以开发，如果对于任意的x∈A，都有f（-x）=f（x），实际上就说明有x就有-x存在，是相对的，也就是定义域是关于原点对称的。所以，通过对定义的开发，我们可以从以下几方面来判断函数的奇偶性：第一，判断定义域，看函数的定义域是否是关于原点对称的；第二，判断f（-x）与f（x）之间的关系；第三，若f（-x）=f（x），则可以判断函数y=f（x）是偶函数，若f（-x）=-f（x），则判断函数y=f（x）为奇函数。

另外还可以运用概念来处理习题，如判断下列函数的奇偶性：

（1）y=f（x）=（x+1）；

（2）f（x）=+

做这类题的时候，如果教师没有将概念讲解清楚，学生仅仅判断f（-x）与f（x）的关系，很容易得出错误的结论。如：（1）f（-x）=f（x），所以判断y=f（x）为偶函数；（2）f（-x）=f（x），函数y=f（x）为偶函数。实际上，对于第（1）题，我们可以判断出函数的定义域是（-1，1]，它的定义域是关于原点不对称的，所以不能够判别奇偶性，对于第（2）题，函数的定义域为[-1，1]，在定义域内f（x）=0，所以该函数既是奇函数又是偶函数[4]。因此，对于教材中的概念一定要开发到位，高度重视，认识到概念的重要性。

三、公式的开发

数学中公式最多，公式也是高中数学体系中重要的一部分，是数学论证与推理过程中的重要依据。有了公式，解题过程就会非常的简单。公式几乎在数学的每一章节中都是必不可少的[5]。在公式的教学中，教师不仅仅要让同学们学会用公式解题，还要了解公式的推导过程。所以公式的开发也是数学教材开发的重要内容。

四、例题的开发

例题是数学课堂的精髓内容，课本例题是教材编写者根据课本的章节内容精心设计的，是对所讲内容的实际运用。课本例题都是非常典型的，具有一定的示范性。一般都是代表了一种解题方法或者数学思想[6]。教材编写的时候考虑到普遍性，所以例题都是比较简单的，在平时的讲课过程中，还需要教师对例题进行二次开发。

例如，在高中必修《基本不等式的证明》一节中，例1：若a是整数，证明不等式a+≥2。本题主要考查的是不等式条件的运用，我们根据公式a+b≥2，就可以证明出上述不等式。这是比较简单的基础运用，下面可以对该例题进行扩展：

扩展1：求函数y=x+（x>0）的最小值；

扩展2：求函数y=x+（x<0）的最大值；

扩展3：求函数y=x+（x>1）的最小值；

扩展4：求函数y=x∈0（1，+∞）的最小值。

例2.设点P是线段P1P2上的点，P1、P2的坐标为（x1，y1），（x2，y2），

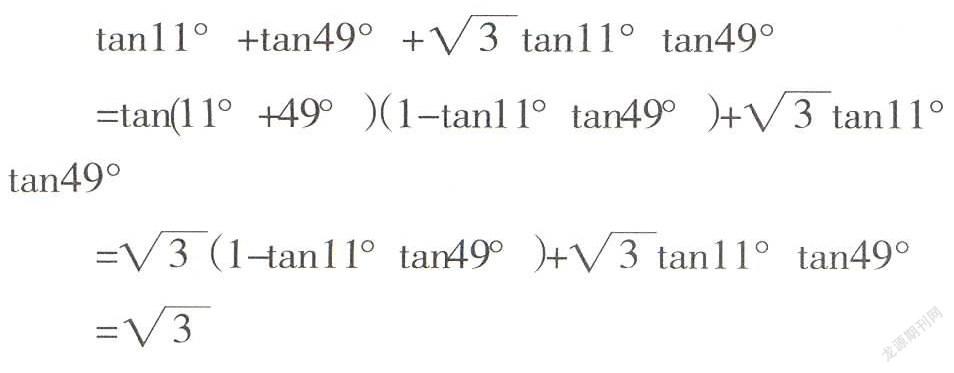
（1）当P在P1P2中点时，求点P的坐标；

（2）当P是P1P2的三等分点时，求点P的坐标。

这个问题比较简单，蕴含着丰富的数学思想，它的解题方法有许多，通过对教材的二次开发，可以培养学生善于思考的习惯。这道题，我们可以将问题扩展为四等分点，五等分点，以至n等分点的坐标。

数学本来就是一门比较难又枯燥的学科，单单对课本内容进行讲解，很难达到学习目标。所以在对知识进行讲解的时候，需要教师用心、用智慧去对课本进行二次开发，帮助学生去理解知识。课本中的例题、公式、概念等都是可以进行二次开发的对象。

参考文献

[1] 张捷.浅议高中数学教材的二次开发[J].基础教育参考，2012（4）.

[2] 李金蛟.数学教材二次开发的原则与路径探微[J].数学通讯，2012（18）.

[3] 吴志鹏.高中数学教材的“二次开发”[J].中国数学教育，2013（Z2）.

[4] 陈亮.高中数学教材二次开发的探索与研究[J].理科考试研究，2015（3）.

[5] 张丽婉.浅谈高中数学教材二次开发的涵义与方法[J].福建中学数学，2014（9）.

[6] 孔祥武.数学教材二次开发使用中的几点建议[J].数学通讯，2011（6）.【责任编辑 郭振玲】