相位量化DRFM欺骗干扰的自适应检测*

刘兴华 罗景青 王文涛

(电子工程学院电子对抗信息处理重点实验室，合肥，230037)



相位量化DRFM欺骗干扰的自适应检测*

刘兴华 罗景青 王文涛

(电子工程学院电子对抗信息处理重点实验室，合肥，230037)

为了从环境中检测出相位量化数字射频存储器(Digital radio frequency memory, DRFM)欺骗干扰的存在，本文设计了一种能够在均匀环境中检测出噪声、干扰或回波信号的自适应检测器。检测过程分为两步：先由基于广义似然比检测(Generalized likelihood ratio test,GLRT)的自适应匹配滤波(Adaptive matched filter,AMF)检测器完成噪声和“信号”(滤波后的回波信号或干扰)的检测；再从回波信号和干扰导引矢量间的差异性出发重新设计检测器，以甄别回波信号或干扰。最后，通过理论推导和蒙特卡洛试验对检测器的性能进行分析和评估，并与透视检测器进行比较。仿真结果表明，在低相位量化位数和高信噪比的条件下，所设计的检测器能够正确检测出干扰信号的存在。

相位量化数字射频存储器；雷达自适应检测；自适应匹配滤波；干扰；广义似然比检测

引 言

数字射频存储器(Digital radio frequency memory,DRFM)是一种用于实现射频信号存储及转发功能的电子对抗(Electronic counter measures,ECM)部件。图1所示为典型的DRFM系统[1]。在对跟踪雷达实施电子干扰的过程中，DRFM对接收到的信号进行高速采样、存储和干扰调制处理，产生与回波信号高度相干的干扰信号，使雷达难以区分回波和干扰。因此，有必要研究一种高效、高正确率的检测器，能检测出DRFM系统产生的欺骗干扰信号，以适应未来电子战的需求。

近年来识别DRFM欺骗干扰的研究主要集中于利用回波和干扰在幅度、双谱和小波变换后的能量比和频率的细微差异来实现干扰检测[2-4]。随着集成电路和DSP技术的发展，便于集成处理的低量化位数的相位量化DRFM被广泛应用于小型化机载系统。文献[5]指出相位量化DRFM还原后的合成信号会产生寄生频率，而从这一特征出发来设计检测器进行检测的研究较少。检测器设计难点在于雷达接收方未知干扰信号的导引矢量。文献[6]定义了干扰导引矢量所属的锥类，并将其作为约束条件，通过解决凸优化问题求出干扰导引矢量的最大似然估计(Maximum likelihood estimate, MLE)，进而基于广义似然比检测(Generalized likelihood ratio test,GLRT)设计检测器。文献[7]在此基础上进行延伸，考虑了回波信号和干扰同时存在时的检测。但是文献[6，7]都需要求解干扰导引矢量的MLE，求解过程繁琐且设计出的检测器形式过于复杂，不适合工程实现。同时文献中没有考虑未知噪声协方差矩阵的情形。本文首先在此基础上详细构建了相位量化DRFM的时域模型，结合自适应检测理论，由辅数据估计环境中噪声的协方差矩阵。然后先运用自适应匹配滤波(Adaptive matched filter,AMF)检测器检验是否为“信号”或噪声，再将文献[6]中锥类的定义拓展到噪声空间作为检验统计量，用于判决回波信号和干扰的存在，而不是基于GLRT去求解干扰导引矢量的MLE来设计检测器。因此，该方法更为简洁，对环境的适应性更强。

图1 DRFM系统Fig．1 DRFM system

1 信号模型

1.1 窄带雷达回波时域模型

脉冲多普勒雷达的RF信号为

(1)

式中：Np表示脉冲个数，幅度A>0，T表示脉冲重复间隔(Pulse repetition interval, PRI)，fc表示载频，φ表示初始相位，p(t)是一个宽度为Tp的矩形函数，Tp≼T。假设目标以恒定速度v运动(v>0)，距雷达的距离为R(t)=R0-v t，R0为t=0时的距离。如果雷达以均匀线阵接收信号，则第一个阵元接收的回波信号为

(2)

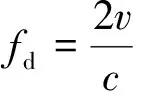
(3)

(4)

1.2 相位量化DRFM欺骗干扰时域模型

如果1.1节中雷达侦察的目标配备有相位量化的DRFM设备，结合假设的雷达信号模型，DRFM设备接收到的雷达信号为

(5)

式中：β∈C，此后β表示在原有值上做任何需要的更新。根据DRFM设备的工作模式，其会对接收的雷达信号高速采样，相位量化并存储，随后添加干扰调制处理还原为模拟信号。还原后的模拟信号可表示为[8]

(6)

式中：f0=fIF+fd/2，fIF为DRFM的中频，Q=2M，M为量化位数。

将还原后的模拟信号进行上变频处理变为射频信号，经发送被雷达阵列第1个阵元接收后的信号为

(7)

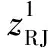
(8)

(9)

综上可得干扰信号时域模型(导引矢量)为

(10)

1.3 信号阵列空时模型

假设均匀线阵的阵元间距为d，阵元数为Na，则阵列的空域导引矢量可表示为

(11)

式中：λ为波长，φ为波达角。那么信号和干扰的空时离散模型(空时导引矢量)为[9]

(12)

式中：⊗表示Kronecker积。

2 检测器设计

对于自适应检测问题，通常将待判断是否存在的目标(信号和干扰)的单元称为待测单元，所接收的数据称为主数据。并将一组与信号和干扰无关且与待测单元有相同噪声统计特性用来估计环境噪声(杂波、热噪声等)的协方差矩阵的数据称为辅数据。用z∈CN×1，N=Nt×Na表示主数据序列，zk∈CN×1,k=1,…,K,K≥N表示辅数据序列，则该检测问题可抽象为

(13)

式中：α,β∈C表示目标/干扰的能量及通道的衰减，是未知确定性参数；k=1,…,k;v,p分别为回波信号和干扰信号的空时导引矢量，v已知，p未知；n和nk为独立同分布的零均值复高斯随机矢量，即n,nk～CNN(0,R)(均匀环境)，协方差矩阵R∈CN×N未知。

对于三元检测问题，通常求解比较复杂，考虑到转化为基带信号的干扰和回波信号频谱的相似性，即谱峰均在fd处，区别在于干扰信号有额外的谱线f′=hQf0(1+v/c)。如果在检测前设计中心频率为fd的窄带滤波器将干扰信号的额外谱线滤除，这样匹配导引矢量v的信号可以是回波信号亦可以是干扰，统称为“信号”。为此就可以将三元假设检验转化为两个二元假设检验,也就是先将假设H1和H2作为一个合成假设H1+H2与H0进行判决，先判断“信号”的有无，再区分H1和H2。对于第一个假设检验，前人已经作了大量的研究，文献[10]中给出了几种经典的算法。本文选择Robust性强的AMF检测器进行判决

(14)

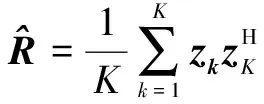
对第2个假设检验，先导出已知干扰导引矢量p和噪声协方差矩阵R时的透视检测器[11]，并将其性能作为未知上述参量时检测的基准(这里的透视滤波器并不是真正意义上的透视滤波器，因为参数α,β未知)。假设H1发生的概率为P1，H2发生的概率为P2，但P1，P2的具体的数值未知。根据GLRT可得

(15)

(16)

式中：门限ηCV=lnγ。实际上，p不是先验知识，透视检测器不可实现。

虽然未知干扰导引矢量p的具体形式，但文献[6]给出了量化干扰和回波导引矢量的误差方式

(17)

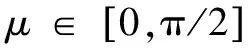
图2 JSEA随量化位数和归一化频率的变化曲线Fig．2 Curve of JSEA versus quantization bits and normalized frequency

根据上面的分析，定义干扰导引矢量所属的锥类C

(18)

式中：0≤ε≤1为门限。考虑环境中的噪声，引申该定义，得到新的检测器如下

(19)

可以看出，该检测器在噪声空间中度量了待检信号和回波信号导引矢量间的夹角余弦的平方值，即通过计算两者之间的相关系数并将其作为识别判断的依据，有较强的物理意义。综上所述，本文所设计的检测器结构如图3所示。

图3 检测器结构Fig．3 Structure of detector

3 检测性能分析

为定量评估检测器的性能，定义虚警概率Pfa=Pr{tAMF>ηAMF|H0}和检测概率PD=Pr{tAMF>ηAMF|H1+H2}。由于第1步检测前，窄带滤波器滤除了干扰信号的多余频谱分量，这时可以认为假设H1近似等同于假设H2。对于AMF检测器，文献[12]指出该检测器具有对噪声协方差矩阵R和回波幅度恒虚警(Constant false alarm rate, CFAR)的特性，并给出虚警概率Pfa和检测概率PD的闭式解，故本节的重点在于分析第2个检测器的性能。

如果H1,H2等可能出现，即P1=P2。那么当假设H1+H2判为真时，其中是H1或H2的概率仍为P1，P2。定义识别概率PR

(20)

(21)

4 仿真试验及分析

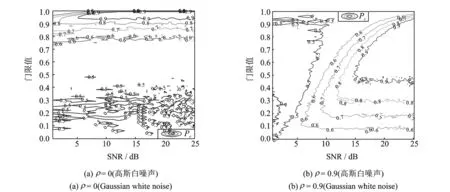
图4 PC随门限和信噪比变化的等值线Fig．4 Contours of PC versus threshold and SNR

为比较不同条件下检测器的性能，设计实验通过估计使PC达到0.9时所需的最低信噪比来间接衡量检测器的性能，同时与透视检测器及文献[6]中的检测器(GLRT-1.2)进行比较。仿真条件除所比较的条件外其他假设不变，做1 000次Monte Carlo实验进行估计，实验结果如表1所示。

从表1可以看出：检测器在白噪声下比色噪声下有更优的检测性能；随着量化位数的增加，无论是在白噪声还是色噪声下所需的最低信噪比在增加，说明检测的难度也随之增加。透视检测器由于已知噪声协方差矩阵和干扰导引矢量，检测性能最优，仿真结果和理论相符；本文设计的检测器和文献[6]中同时对于公式中提到的相位量化后附加时延t0和辅数据样本数K都会影响检测性能。随着t0和K的增加，检测效果会相应提到的检测器两者性能差别不大，但是检测器的结构得到了明显简化，更为有效。得到改善。

表1 PC=0.9时各条件下所需最低信噪比

5 结束语

本文针对相位量化DRFM欺骗干扰的检测问题，从分析回波信号和相位量化DRFM欺骗干扰的空时导引矢量出发，通过两个检测器分两步完成对回波信号、噪声和干扰的检测，达到了检测相位量化DRFM欺骗干扰的目的。仿真结果验证了所设计的检测器对相位量化DRFM欺骗干扰检测的有效性，同时也表明在高量化位数的条件下，运用该方法不能检测出相位量化DRFM欺骗干扰信号，由于该检测器结构简单且对环境有自适应性，因此，具有一定的工程应用价值。但本文只分析了均匀噪声环境下DRFM干扰信号的检测且所需信噪比较高，考虑非均匀噪声并设计低信噪比的检测器将是下一步的改进方向。

[1] Greco M, Gini F, Farina A, et al. Effect of phase and range gate pull-off delay quantization on jammer signal[J]. IEE Proceedings Radar, Sonar and Navigation, 2006, 153(5):454-459.

[2] Zhang Jindong, Zhu Daiyin, Zhang Gong. New antivelocity deception jamming technique using pulses with adaptive initial phase[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2):1290-1300.

[3] 田晓,唐斌.基于归一化小波分解能量比的雷达有源欺骗干扰识别[J].数据采集与处理,2013,28(4):416-420.

Tian Xiao, Tang Bin. Active deception jamming recognition of radar based on normalized wavelet decomposition power ratio[J].Journal of Data Acquisition and Processing,2013,28(4)：416-420.

[4] Li JianXun, Shen Qi, Yan Hai. Signal feature analysis and experimental verification of radar deception jamming[C]//IEEE CIE International Conference on Radar. Chengdu, China: IEEE, 2011:230-233.

[5] Greco M, Gini F, Farina A. Combined effect of phase and RGPO delay quantization on jamming signal spectrum[C]// IEEE International Radar Conference. Arlington, USA: IEEE, 2005:37-42.

[6] Greco M, Gini F, Farina A. Radar detection and classification of jamming signals belonging to a cone class[J]. IEEE Transactions on Signal Processing, 2008, 56(5):1984-1993.

[7] 孙闽红, 唐斌. 雷达DRFM欺骗干扰的检测[J]. 信号处理, 2010, 26(5):672-676.

Sun Minhong, Tang Bin. Detection of radar DRFM deception jamming[J]. Signal Processing, 2010, 26(5):672-676.

[8] Bandiera F, Farina Alfonso, Orlando D, et al. Detection algorithms to discriminate between radar targets and ECM signals[J]. IEEE Transactions on Signal Processing, 2010, 58(12):5984-5993.

[9] Bandiera F, Orlando D, Ricci G. Advanced radar detection schemes under mismatched signal modals[M]. New York: Morgan&Claypool Publishers, 2009:1-39.

[10]Gao Yongchan, Liao Guisheng, Zhu Shengqi, et al. Persymmetric adaptive detectors in homogeneous and partially homogeneous environments[J].IEEE Transactions on Signal Processing, 2014,64(2):331-342.

[11]Steven M K. Fundamental of statistical signal processing: Detection theory[M]. Upper Saddle River: Pearson Education, 1993:189-267.

[12]Robey F C, Fuhrmann D R, Kelly E J, et al. A CFAR adaptive matched filter detector[J]. IEEE Transactions on Aerospace and Electronic Systems,1992,29(1): 208-216.

[13]Kraut S, Scharf L L. The CFAR adaptive subspace detector is a scale-invariant GLRT[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2538-2541.

Adaptive Detection of Phase Quantized DRFM Deception Jamming

Liu Xinghua， Luo Jingqing， Wang Wentao

(Laboratory of Electronic Countermeasure and Information Processing,Electronic Engineering Institute, Hefei, 230037, China)

To detect the phase quantized digital radio frequency memory (DRFM) deception jamming in realistic radar scenarios, an adaptive detector for detecting noise, jamming or echo signal in homogeneous environments is designed. Firstly noise or ″signal″ (filtered echo signal or jamming), is detected through adaptive matched filter (AMF)detector based on generalized likelihood ratio test (GLRT). Then the difference between two space-time steering vectors of echo signal and jamming is used to redesign the detector to discriminate the echo signal or the jamming. The detector performance is assessed and analyzed through Monte Carlo simulation and theory deriation, which is compared with clairvoyant detector.Simulation results show that the detector can correctly detect the jamming signal under conditions of low quantization bits and high signal-to-noise (SNR).

digital radio frequency memory(DRFM); adaptive radar detection; adaptive matched filter(AMF); jamming; generalized likelihood ratio test(GLRT)

2014-03-27；

2014-10-16

TN974

A

刘兴华(1993-)，男，硕士研究生，研究方向: 空间信息处理，E-mail：xinghua217@gmail.com。

罗景青(1957-)，男，教授，博士生导师，研究方向：空间信息处理、阵列信息处理和电子对抗信息处理。

王文涛(1989-)，硕士研究生，研究方向：雷达信号处理。