基于入射散射极化优化的抗箔条干扰方法*

党晓江 李政杰 李 欣

(1.空军工程大学防空反导学院，西安，710051;2.94175部队，乌鲁木齐，830000)



基于入射散射极化优化的抗箔条干扰方法*

党晓江1,2李政杰1李 欣1

(1.空军工程大学防空反导学院，西安，710051;2.94175部队，乌鲁木齐，830000)

国内外的大多数研究没有综合考虑入射极化对散射幅度、散射极化的定量影响。通过构建雷达视线方向非相干箔条云瞬时极化散射模型，获得了一组特定入射条件下的极化散射统计数据，并对其进行基于极化坐标系扭曲的处理，同时讨论了箔条云对入射极化的选择特性。数值仿真结果表明，当扭曲因子较大时，处理后的极化状态概率近似分布在水平极化域，同时雷达俯仰角较小时，箔条云对入射极化具有良好的选择性。本文结论可以作为极化抗箔条干扰的初级优化方案，为极化滤波等后续极化信息处理打下基础。

箔条云；极化散射；极化选择；极态密度；数值仿真

引 言

在现代电子对抗中，箔条云是一种有效、可靠的无源干扰形式[1]，严重影响着雷达的正常工作，充分利用极化信息可以有效地抑制干扰。箔条云可看作大量随机运动的偶极子集合体，用确定的方法研究箔条云的电磁散射问题很困难，往往借助统计的手段[2]研究箔条云回波的极化散射特性。在忽略一些条件的非相干箔条云极化散射模型[3]中，可以认为偶极子之间极化散射特性互不干扰，不同偶极子散射极化是服从同分布的随机变量，箔条完全散开后，回波极化统计特性平稳，因此基于非相干散射模型的箔条云极化散射是一个平稳的随机过程。

图1 竖直方向与雷达视线方向极化散射坐标系的关系示意图Fig.1 Polarimetric scattering axis relationship between verticalness and radar sight

优化入射、散射极化方式和极化滤波等极化信息处理技术结合起来，能使极化抗干扰效果更好。文献 [4-8]都考虑不同极化通道下(HH，VV，HV，VH)箔条云的极化散射统计特性，这种获取回波信息的输入输出模式可以称作“离散极化通道加散射能量”，这种模式没有考虑到更多的入射和散射极化信息，限制了对极化信息的充分利用。由于箔条云在散开后其空间姿态具有稳定的分布特性及其线极化散射等特性，对入射波的极化状态特别敏感，从抗干扰的角度来讲，优选入射波极化使散射回波幅度尽可能小很有必要。在干扰抑制极化滤波器(Interference suppresion polarization filter，ISPF)设计中，首要解决的是干扰极化状态的估计问题[9]，但如果已知箔条云的空间姿态分布，可根据输入输出条件通过计算机仿真得到箔条回波极化状态分布，箔条回波极化状态往往不是单一的，而是群集在极化域的子域——线极化域，这在很大程度上降低了ISPF的滤波性能[10]，因此需要在干扰信号通过ISPF之前对获取的干扰极化信息进行预处理才能使极化滤波器的滤波性能达到最佳。文献[11,12]提出了一种基于水平垂直极化分量幅度实数加权的极化变换算法，但是雷达目标回波极化状态水平或垂直极化的条件比较苛刻，并且没有考虑从统计的观点来说明极化状态变换前后的密集程度发生了怎样的变化。文献[13]提出的基于酉空间级联变换的极化状态变换算法普适性很强，能对极化域的任何极化状态群进行状态变换，但是由于箔条云的线极化散射特性，若提出基于欧氏空间的极化变换算法既能满足变换需要又能简化运算量，因此很有必要,以此为背景，为了达到有效抑制干扰的目的，本文构建获取箔条云回波极化信息的输入输出模式为“入射极化加散射能量加散射极化”， 对散射极化状态进行基于极化坐标系拉伸扭曲的预处理，研究使回波能量尽可能小的入射极化选择方式。

1 基于庞加莱极化域的箔条偶极子散射原理

采用后向散射坐标系(Back scattering axis, BSA)的约定，建立极化散射坐标系，坐标原点位于偶极子中心，如图1所示。雷达视线垂直于水平散射平面的极化散射矩阵直接引用文献[4]的结果

(1)

设入射极化状态为Einput，用极化相位描述子来表示

Ji=RCi

(2)

散射极化Stokes矢量Js可以表示成

Js=MJi

(3)

(4)

将gs用散射波极化相位描述子来表示

(5)

任取两个等式可以解得

(6)

式中:F1，F2为该式(5)的映射函数。

2 散射模型及信息提取

2.1 雷达视线方向非相干箔条云散射模型

图2 旋转前和旋转后的极化坐标系示意图Fig.2 Primary axis and rotated polarimetric axis

雷达视线通常不垂直于水平散射平面，与水平散射平面的夹角是变化的，建立这种情况下的关于雷达俯仰角的动态散射矩阵更具有工程意义。如图1所示，假设雷达视线相对于X轴的方位角和俯仰角分别为αR，βR，通过欧氏空间的坐标变换，将入射方向旋转至图 1中雷达视线方向。旋转后的极化散射坐标系如图2所示，设在新坐标系中偶极子方位角和俯仰角分别为α′，β′。

变换后，散射方向即雷达视线方向和散射平面都发生了变化，但是相对位置没有变化，故在新坐标系中散射矩阵S′的形式与式(1)完全相同，即有

(7)

这里由于篇幅的限制不给出变换过程的中间过程，直接给出变换矩阵

(8)

使得

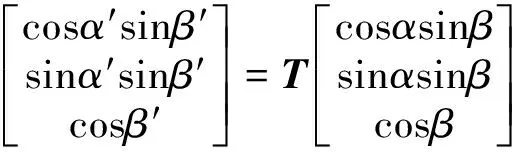
(9)

该式有两个未知变量，可以解得

(10)

式中：f1，f2为式(9)的映射函数。将式(10)代入式(7)便得到偶极子雷达视线方向的散射散射矩阵。

在非相干散射模型[3]中，偶极子之间散射特性互不干扰。假设箔条数目为N，则每一根箔条的方位角α和俯仰角β各自服从同分布、独立的随机变量，N根箔条的方位角和俯仰角可以看作是以n为离散参量的平稳随机过程，数学表达式如下

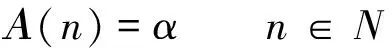
(11)

(12)

式(11,12)表示当n取确定的某一个值时，A(n),B(n)代表一个随机变量，当n在1～N之间取动态值时，表示一个平稳过程。从随机过程的角度讲，在某一瞬间，各根箔条的空间姿态角的集合就是随机过程的样本集，用α(n)，β(n)表示，n=1,2,…,N，又因为两个姿态角各自服从同分布，且不同偶极子之间相互独立，因此两个样本集相当于两个随机变量α和β的产生的N点随机数，这样就把非相干箔条云瞬时极化散射特性和单个偶极子的极化散射统计特性联系起来。

将式(11，12)代入式(10)，得

(13)

将式(13)代入式(7)，当n=1,2,…,N时得到的即为非相干箔条云的瞬时散射矩阵，用S′(n)表示。由此可得雷达视线方向非相干箔条云瞬时stokes统计矢量

(14)

2.2 特定入射条件下散射极化信息提取

对应于频域上的频点的概念，可以在极化域上定义极点：每一个极化状态在庞加莱球上有一个点与它对应，这个点就可称作极点。单位庞加莱球只能表征极态，无法表征不同极点处的散射幅度，因此，对应于频谱，可以提出极谱的概念来更好地表征散射波极化统计特性。极谱表示为

(15)

式中：(η，φ)为极化相位描述子，在η，φ平面内的坐标代表极点；G0代表该极点处的幅度；g为归一化子矢量。极带是极谱中由特定极点围起来的面积区域，这一点与频带有本质的区别，极带越小，极化状态越集中。

由于S′(n)是一个随机过程，故散射波极化状态和散射幅度是随机变量，S′(n)的统计特性依赖于偶极子空间姿态角α和β的分布特性，以文献[2]中给出的方位角服从均匀分布、俯仰角服从正态分布的空间姿态为例讨论问题。

方位角为均匀分布

(16)

俯仰角为高斯分布

(17)

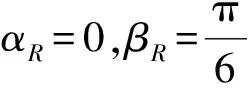
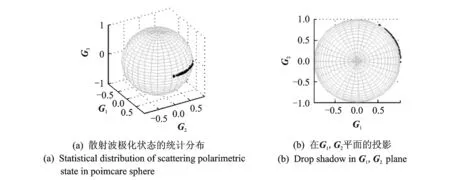
图3 散射波极化状态在宠加莱球上的统计分布Fig.3 Scattering polarimetric state distribution in Poimcare sphere

图4 散射波极谱、散射幅度和散射相位描述子的概率密度Fig.4 Polarimetric spectrum, propability density curves of scattering amplification and phase descriptor

图5 水平方向箔条云对入射极化的瞬时选择性 Fig.5 Chaff′s instantaneous polarimetric selectivity characteristic in horizontal direction

从图3可以看出，箔条云散射极化状态处于庞加莱极化域的子域——线极化域中，从图4的极谱和概率密度曲线可以看出散射幅度和散射相位描述子具有统计特性，不是确定的值，散射幅度在0．3λ2附近的概率最大，变化幅度将近0．5λ2，散射相位描述子ηs在14°附近的概率最大，极带宽度为30°左右，总体来说散射极化偏向于水平极化。

3 抗箔条干扰的最优入射极化

从抗干扰的角度讲，散射幅度越小、散射极态越集中越好。箔条云偶极子空间姿态的分布特性，决定了箔条云在特定频率、特定雷达视角条件下对入射波极化具有选择性。针对箔条云对入射极化的选择性，选择合适的入射极化方式，和极化滤波等极化信息处理技术结合起来，能使抗干扰效果更好。由于箔条云的线极化散射特性，入射极化域缩小为线极化域(即ηi=0)，当ηi遍历整个线极化域时，散射幅度G0s和散射相位描述子ηs的变化趋势可以作为散射波对入射极化的选择依据，如图5所示。

图6 雷达视线方向G0s和ηs对入射极化的瞬间选择性Fig.6 Instantaneous polarimetric selectivity characteristic of G0s and ηs in radar sight

4 基于极化坐标系扭曲的干扰极化信息预处理

由于目标散射极化状态在极化域的聚集度不高，在很大程度上降低ISPF的滤波性能，因此需要在干扰信号通过ISPF之前对获取的干扰极化信息进行预处理才能使极化滤波器的滤波性能达到最佳。本文提出一种基于极化坐标系扭曲拉伸的算法将直角极化坐标系中的极化状态映射到扭曲坐标系，实现状态距离减小并搬移，大大改变了极态的聚集度。由于箔条云的线极化散射特性，只需建立二维散射坐标系即可。

图7 扭曲坐标系中两基向量夹角与扭曲因子的关系Fig.7 Relationship between included angle of two base vectors and warped factor

(18)

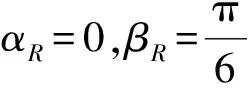
(19)

通过MATLAB仿真得到处理前后极态密度统计分布曲线和极态在庞加莱球上的分布，取s为1 000，如图8所示。从图8可以看出处理前极态分布较分散，在atan(G2/G1)≈28°处，极态密度最大，约有1．5%的极态分布在该位置，处理后极态接近100%分布在atan(G2/G1)≈0°处，极化状态高密度集中在水平线极化域。文献[11]在Jones极化域对干扰的水平和垂直两极化分量进行实数加权，在理论上分析了当信号极化状态为水平或垂直极化时如何选择加权因子的问题，并没有给出仿真结果。文献[13]提出了基于酉空间的极化变换算法，从仿真结果来看，效果很好，但是由于箔条云的线极化散射特性，其散射极化信息处于线极化域，若采用上述算法，会带来“大算法小运算”的缺陷。因此，本文提出的基于极化坐标系扭曲的极化变换算法更加适合于对箔条云干扰回波极化信息的处理。

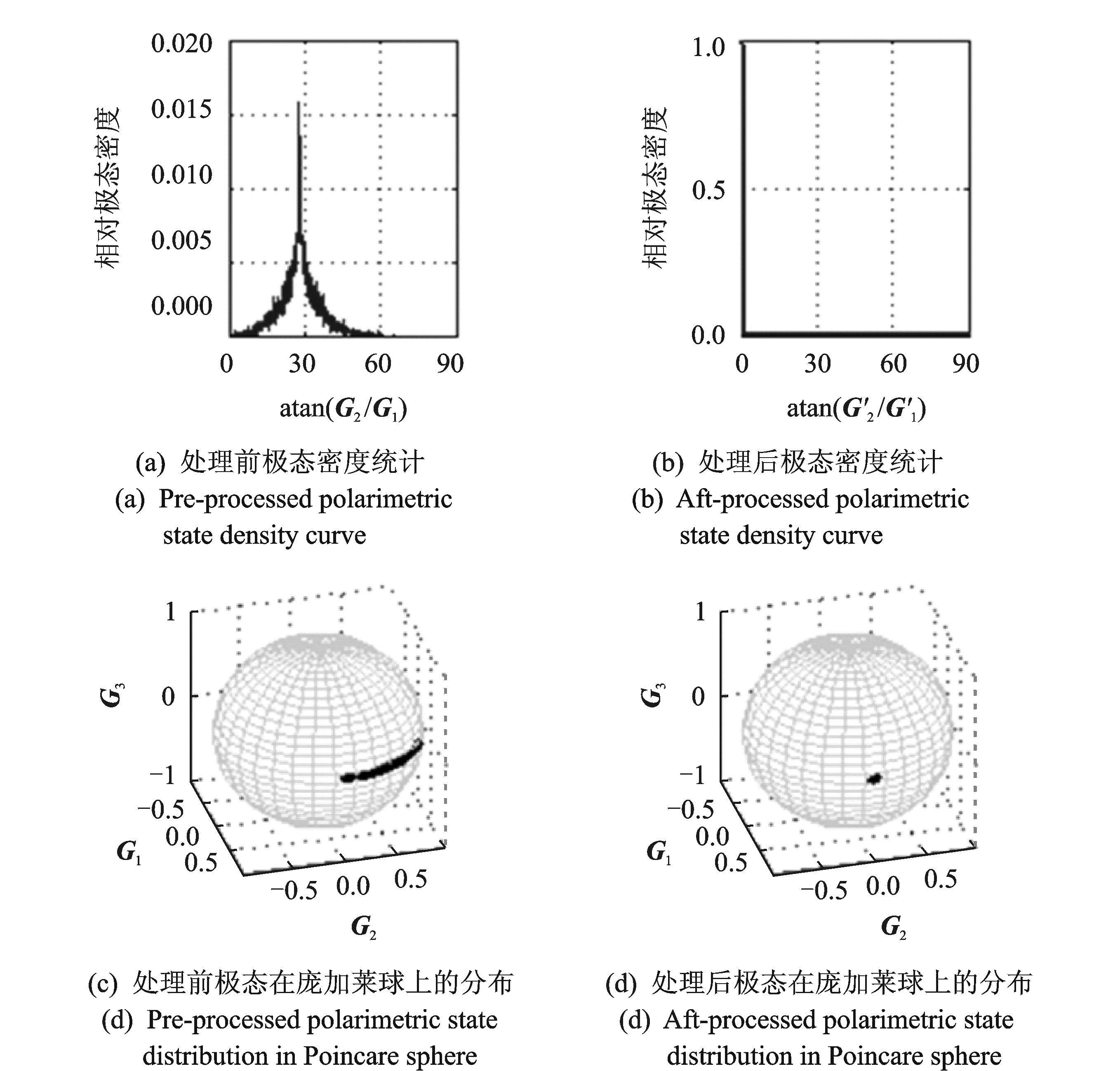
图8 处理前后极态密度统计曲线和极态在庞加莱球上的分布(s为1 000)Fig.8 Pre-and-aft processed polarimetric state density curve and polarimetric state distribution in Poincare sphere (s=1 000)

5 结束语

本文通过构建雷达视线方向非相干箔条云极化散射模型，获得了一组特定入射条件下的极化散射数据，并对其进行基于极化坐标系扭曲的处理，同时讨论了箔条云对入射极化的选择特性。数值仿真结果表明：(1)雷达俯仰角越小，水平正态分布的箔条云对入射极化的选择性越好，选择垂直极化入射波时，能最大程度地减小散射幅度，与文献[12]的结论相吻合。(2)当扭曲因子s为1 000时，处理后的极化状态以概率近似为1分布在水平极化域，解决了文献[10]因干扰极化状态分散而降低ISPF滤波性能的困扰。本文充分利用了入射极化、散射幅度和散射极化信息，优化了极化抗箔条干扰的初级方案，为极化滤波等后续极化信息处理打下理论基础。

[1] 陈静.雷达箔条干扰原理[M].北京:国防工业出版社，2007.

Chen Jing. Principle of radar chaff jamming[M]. Beijing: National Defense Industry Press, 2007.

[2] 刘涛.瞬态极化统计理论及应用[D].长沙：国防科学技术大学,2007:389-395.

Liu Tao. Theory and application of instantaneous statistic polarization [D]. Changsha: National Defense Science and Technology University, 2007:389-395.

[3] 王雪松，周颖,张义容，等.偶极子云团的非相干极化散射特性[J].电波科学学报，2000,15(3):289-293.

Wang Xuesong, Zhou Ying, Zhang Yirong. Study on non-coherent polarization scattering characteristics of dipole clouds[J]. Chinese Journal of Radio Science, 2000,15(3):289-293.

[4] 李金梁，王雪松，李永祯.箔条云散射的极化统计特性[J].电子学报，2010，3,38(3)：714-719.

Li Jinliang, Wang Xuesong, Li Yongzhen. Polarimetric statistic characteristics of chaff cloud scattering[J]. Electronic Journals, 2010,38(3)：714-719.

[5] 贺兴建.箔条雷达散射截面的极化特性[J].山西师范大学学报，1999,13(4):27-30.

He Xingjian. Polarimetric characteristics of RCS of chaff cloud[J]. Journal of Shanxi Normal University, 1999,13(4):27-30.

[6] 李金梁，王雪松，李永祯.正态空间取向箔条云的极化特性[J].电波科学学报，2008,23(3):289-296.

Li Jinliang, Wang Xuesong, Li Yongzhen. Polarization characteristics of Gaussian oriented chaff clouds[J]. Chinese Journal of Radio Science， 2008,23(3):289-296.

[7] Wong J L, Reed I S, Kaprielian Z A. A model for the radar echo from a random collection of rotating dipole scatterers[J]. IEEE Trans on AES, 2004,40(1):93-102.

[8] Marcus S W. Dynamics and radar cross section density of chaff clouds[J]. IEEE Trans on AES, 2004,40(1):93-102.

[9] 焦程鹏.基于卡尔曼滤波的自适应极化参数估计方法[J].数据采集与处理，2008，23(4)：476-480.

Jiao Chengpeng. Polarization estimation approach based on Kalman filtering technique[J]. Journal of Data Acquisition and Processing, 2008，23(4)：476-480.

[10]杨运甫,李明军.极化滤波器的性能比较[J].中国电子科学研究院学报，2007，2(6)：640-643.

Yang Yunfu, Li Mingjun. Performance comparison of polarization filter[J]. Chinese Electronic Science Research Institute, 2007，2(6)：640-643.

[11]张国毅,刘永坦.水平或垂直极化雷达抗干扰能力的提高[J].现代雷达，1999,21(5):1-10.

Zhang Guoyi, Liu Yongtan. Enhancement of anti-interference of horizontal and vertical[J]. Modern Radar, 1999,21(5):1-10.

[12]唐毓燕.对抗箔条云的最佳收发极化方式[J].雷达与对抗，2000，X(2)：8-17.

Tang Yuyan. Optimal receive-transmit polaremetric form of anti-chaff cloud[J]. Radar and Antagonism, 2000，X(2)：8-17.

[13]代大海，王雪松，肖顺平,等.电磁波极化变换的数学原理及性质[J].中国科学G辑，2008，38(10)：1301-1311.

Dai Dahai, Wang Xuesong, Xiao Shunping, et al. Mathematic principle & property of polarimetric transform of electromagnetic wave[J]. Chinese Science G, 2008,38(10):1301-1311.

Anti-chaff Method Based on Optimizing Polarization of Incident and Scattering Form

Dang Xiaojiang1,2, Li Zhengjie1, Li Xin1

(1. Air and Missile Defense College, Air Force Engineering University, Xi′an, 710051, China; 2. PLA Unit 94175, Urumqi, 830000, China)

Most research for anti-chaff using polarimetric information at home and abroad are considered without the influence of incident polarization both on scattering amplitude and scattering polarization. So a group of polarimetric scattering statistical data in given incident conditions is acquired and processed based on polarimetric coordinate warped, and preferential statistic curves of chaff cloud aiming at incident wave polarization form are also achieved through building a instantaneous polarized scattering mode of noncoherent chaff cloud in radar sight direction. Numerical simulation results show that the processed polarization states almost totally distribute on horizontal polarimetric area and chaff cloud has statistic preferential characteristics when incident polarization is at a minor angle of pitch of radar. Conclusions can be regarded as primary optimizing projects for anti-chaff using polarimetric information and provide the theoretical base for the polarization filtering.

chaff cloud; polarimetric scattering; polarimetric preference; polarization state density; numerical simulation

2014-04-22；

2014-07-05

TP391

A

党晓江(1988-)，男，硕士研究生，研究方向：雷达目标极化特征提取及处理，E-mail:xiaojiang3413@163.com。

李政杰(1959-)，男，教授，研究方向：雷达对抗。

李欣(1989-)，男，博士研究生，研究方向：航迹欺骗抗干扰。