基于游程特征的线性分组码与卷积码类型识别*
李歆昊 张 旻 史英春 袁 泉
(1.电子工程学院705教研室,合肥,230037; 2.电子工程学院电子制约技术重点实验室,合肥,230037)
基于游程特征的线性分组码与卷积码类型识别*
李歆昊1,2张 旻1,2史英春1,2袁 泉1,2
(1.电子工程学院705教研室,合肥,230037; 2.电子工程学院电子制约技术重点实验室,合肥,230037)
针对线性分组码与卷积码的类型识别问题,本文提出了一种基于游程特征的信道编码类型识别方法。论文从理论上分析了两种编码游程特性存在的差异,即卷积码的游程具有较好的随机性而线性码游程的随机性较差,并且线性码在信息位长度附近的游程数会发生一定的畸变。通过提取编码的游程特征,算法实现了对这两种编码类型的识别。仿真结果验证了所提识别方法的有效性和鲁棒性,表明算法具有一定的工程应用前景。
编码识别;线性分组码;卷积码;随机性;游程分布
引 言
为了实现通信的可靠性并提高通信的效率,信道编码在数字通信中得到了普遍的应用。信道编码及其识别技术不仅在智能通信、卫星通信和认知通信领域有广阔的应用前景,而且在通信对抗和网络对抗领域也有迫切的军事需求,因此越来越引起人们的重视[1-5]。
信道编码识别的算法主要分为线性分组码识别和卷积码识别。线性分组码的识别算法主要包括基于码根信息差熵函数的算法[6]、基于有限域同构原理的算法[7]、基于Walsh-Hadamard变换的算法[8]和基于码重分析法的算法[5]等。卷积码的识别算法主要包括基于改进欧几里德算法[9]、基于容错矩阵分解的算法[5]、基于Walsh-Hadamard变换的算法[10]和基于高斯法解方程的算法[5]等。它们都是通过一定的手段,在已知编码类型的基础上实现对编码参数、生成多项式和校验矩阵的识别。然而在实际的非合作通信领域,接收序列的编码类型往往是未知的,这就为选择合适的算法造成了困难。此外在通信对抗领域,若能确认对方通信系统使用的信道编码类型,就可以选择相应的干扰方法,如对使用卷积码的通信系统,可采用产生突发错误为主的干扰方法,实现高效干扰[5,11]。由此可见,实现对编码类型的识别具有重要的意义,但目前在此方面的研究成果还不多。本文从理论上分析了线性分组码与卷积码的游程特征差异,通过提取游程特征实现了线性分组码与卷积码编码类型的盲识别。仿真实验表明,在高误码率的情况下,算法仍然具有较好的识别效果。
1 线性分组码与卷积码的基本概念
1.1 线性分组码的基本概念
将信息码元分组,为每组信息码附加若干监督码的编码称为分组码。若每个监督码元都是由码组中某些信息码元线性相加得到的,则称这样的分组码为线性分组码,它的编码器模型如图1所示[12]。M为编码器的输入,称为信息位,它由k位码元组成。C为编码器的输出,称为码字矢量,它由n位码元组成,其中有k位信息元,r=n-k位校验元,并且每组码字的校验元仅与本组的信息元有关,与其他组无关[12]。

图1 线性分组码编码器结构Fig.1 Linear block code encoder structure
1.2 卷积码的基本概念
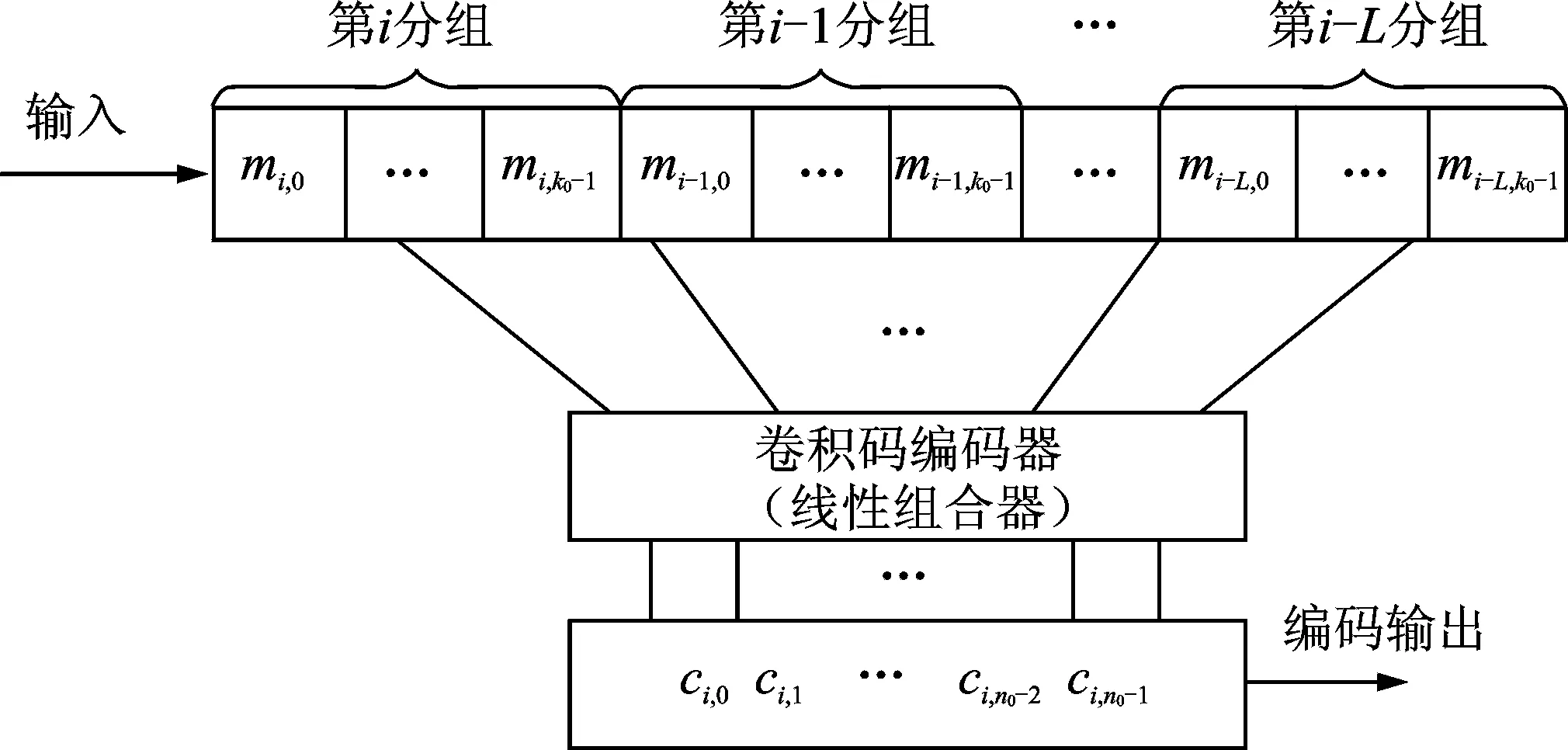
图2 卷积码编码器结构Fig.2 Convolutional code encoder structure
对于一个卷积码的编码器,输入长度为k0的信息序列,经过串并变换至离散线性系统的k0个输入端。系统的输出端有n0个,且延迟为m,输出的n0个编码数字通过并串变换后送入信道完成编码。称这种(n0,k0,m)的码字为卷积码[13],如图2所示。由图2可知,第i时刻输入至编码器的信息组mi及其相应的码段ci,不仅与前m个码段中的码元有关,而且也参与了后m个码段中的校验运算,因此用编码约束长度N表示卷积码编码过程中相互约束的码元个数,对于(n0,k0,m)卷积码,其编码约束长度N=n0(m+1)。
2 序列的游程特征分析
2.1 二进制随机序列的游程特性
定义1 设a是GF(2)上周期为v的周期序列,将a的一个周期a=(a0,a1,a2,…,av-1)依次按循环排列,使av-1与a0相邻,则把如100…001和011…110的一连串两两相邻的项分别称为a的一个周期中的一个0游程和1游程。0游程中的0的个数或1游程中1的个数称为这个游程的长[5]。
定义2 随机比特序列Xn特指长度为n的比特序列,序列元素取比特值0或者1。用符号表示为
(1)
定义3 随机数R则是一个取自广义随机数序列Rn的数字。该广义随机数序列Rn的元素取值为实际应用中要求的定义域内任意值。用符号表示为
(2)
此外,随机比特序列Xn与0,1个数和游程有如下两条性质[5]:
(1) 在周期为2n-1的0,1序列的一个周期中,若某一元素的个数为2n-1个,则另一个的个数就为2n-1-1个。
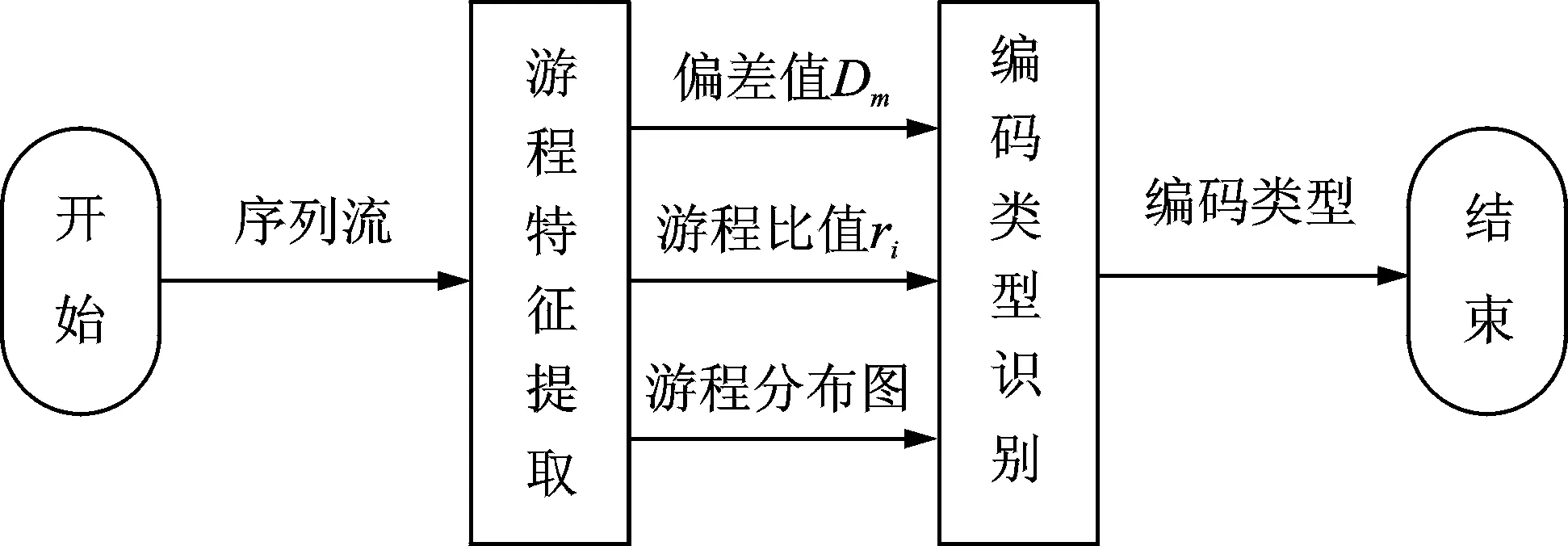
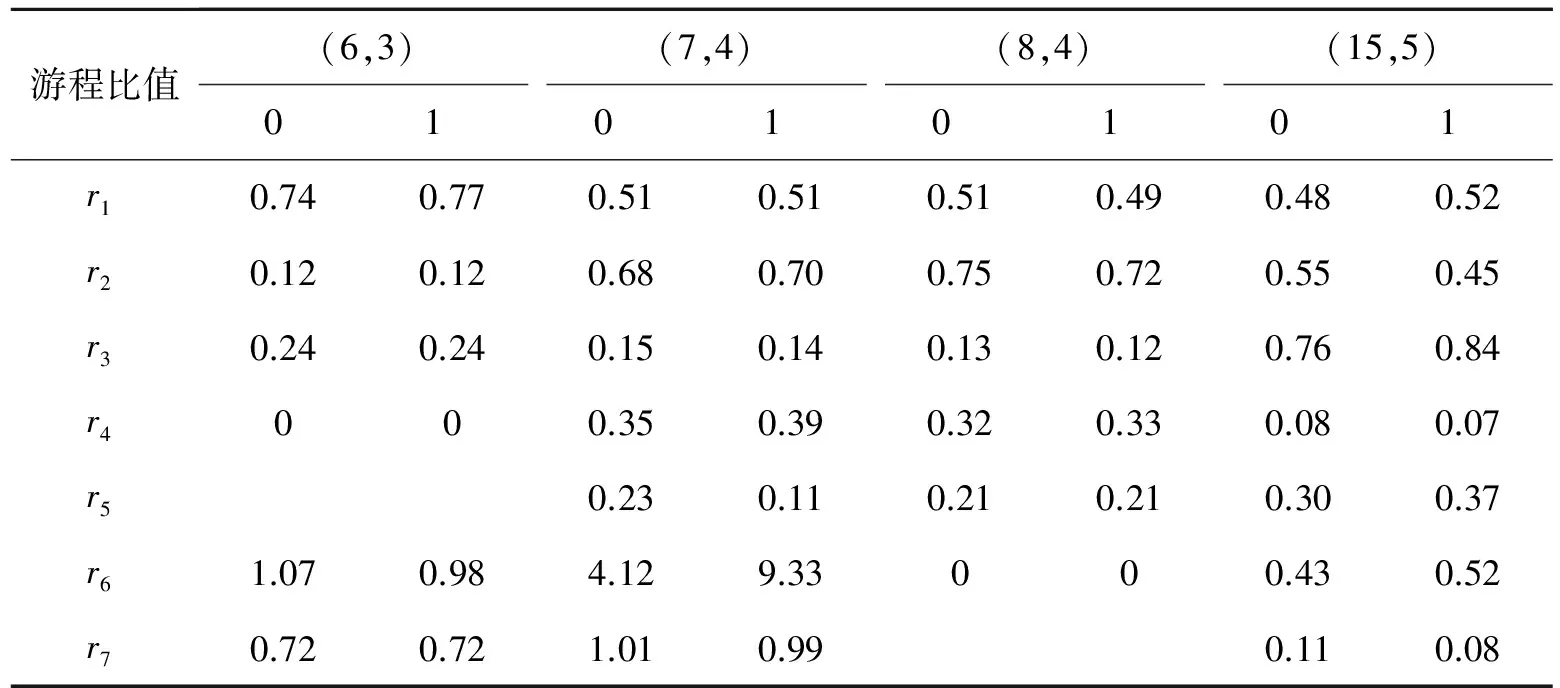
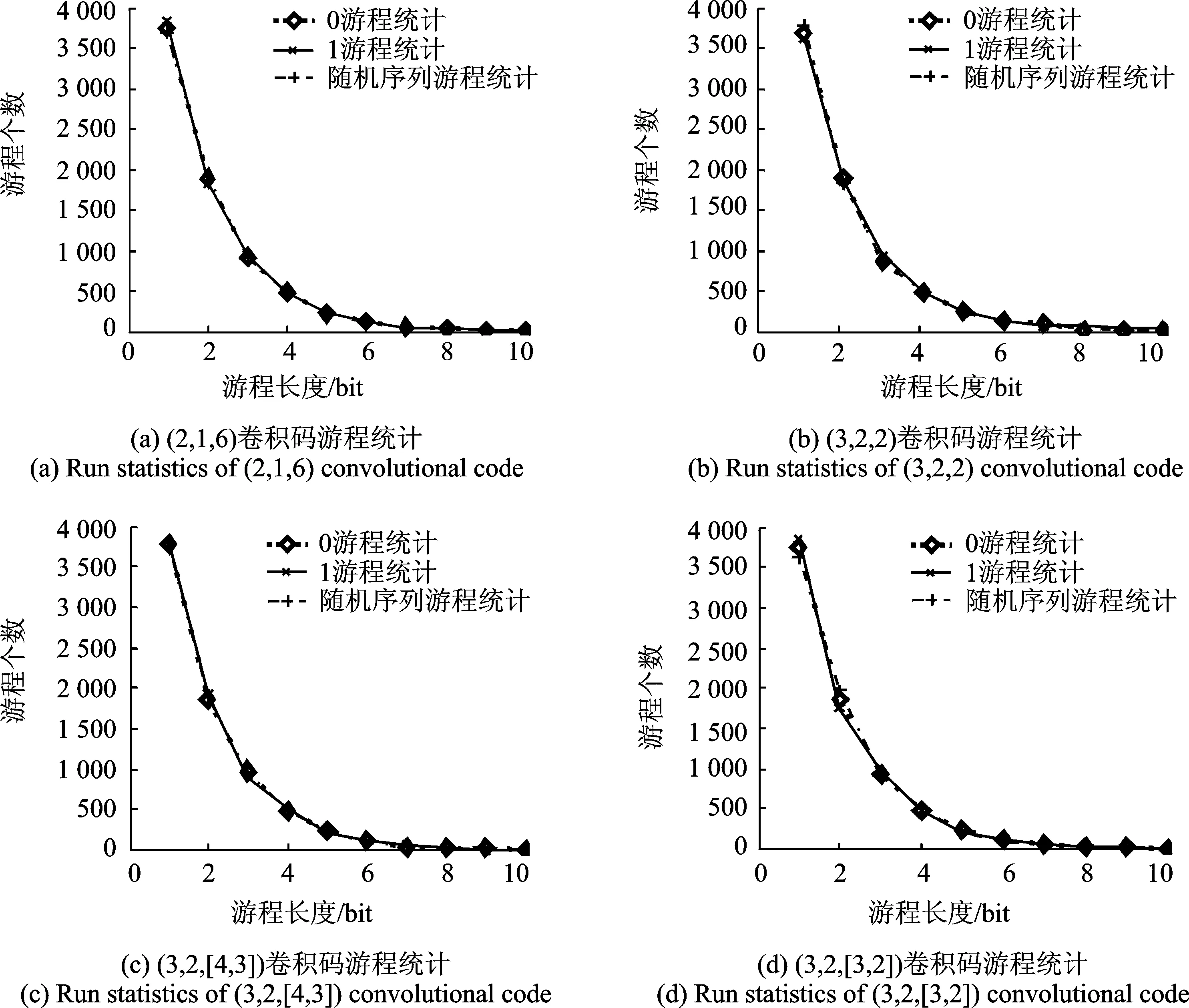
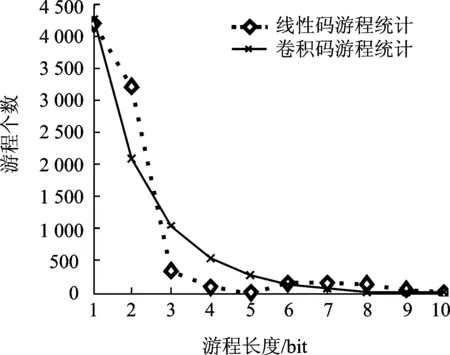
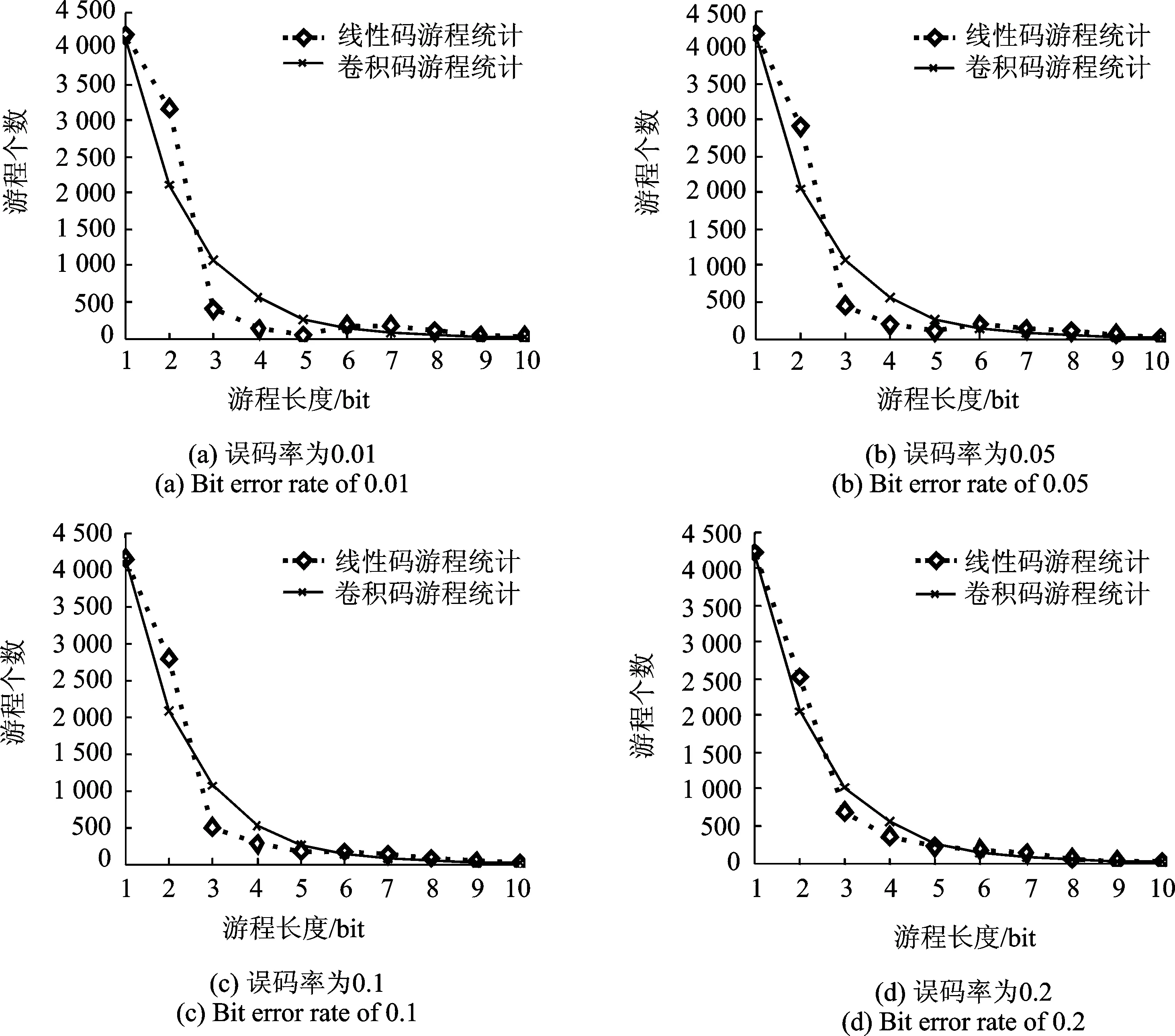
(2) 对周期为2n-1的序列,在其一个周期内,游程总共有2n-1个,其中0游程个数和1游程个数各占一半。长度为k(0 由此可见,随着游程长度的递增,随机序列的0,1游程数按照1/2规律递减,而且相同游程长度下的0,1游程数基本相等。 2.2 线性分组码与卷积码的随机性分析 2.2.1 线性分组码的随机性 对于(n,k)的二元编码来说,k位信息码元共有2k个不同组合,输出的码字矢量也应当有2k种,如图3(a)所示。对于长度为n的二元随机序列,共有2n个可能的码字矢量,如图3(b)所示。可见(n,k)编码有2n-2k个禁用码字,破坏了线性分组码的随机特性,导致线性分组码的随机性能变差。因为信息元的k位是可以随机产生的,所以游程长度小于k的游程可以在码字中得到,而长度大于等于k的游程只有可能在两个码字的拼接处得到。因此,与随机序列的游程相比,线性分组码的游程长度在信息位附近会发生较大畸变,不再呈现1/2的递减规律。 以(6,3)线性分组码的1游程为例,它的许用码字如图4所示。当游程长度t=4(信息位长度k=3)时,此种游程长度的序列只有码字011011和码字110110首尾相接时才能得到,其出现概率p'=(1/23)×(1/23)。此时,该游程长度下的游程出现概率仅为完全随机序列的1/8,游程数与随机序列相比差别很大。 2.2.2 卷积码的随机性 与线性分组码相比,卷积码最大的不同就是具有记忆性[14]。当信息序列被切割成长度为k0的一个个分组后,编码时本组的n0-k0个校验位不仅与本组的k0个信息元有关,而且还与以前各时刻输入至编码器的信息元有关,如图2所示[5]。因此,每组码字中的校验位不再由信息位唯一确定,并且卷积码序列由移位寄存器产生得到,而移位寄存器生成的序列具有很好的随机性[15]。因此,卷积码的随机性较好,表现在游程特征上就是随着游程长度的增加,0,1游程的数量呈现出1/2的递减规律。 图3 码字分布图Fig.3 Codeword distribution 图4 (6,3)线性分组码码字Fig.4 (6,3) linear block codeword 2.2.3 基于游程的识别方法 现有的序列随机性检测方法很多,如单比特频率检测、块内频率检测、非重叠模板匹配检测、近似熵检测和游程检测等[5],它们都只能从某一方面评估序列的随机性。除游程特征以外,线性分组码与卷积码的其他随机特征差别不大。通过2.2.1节与2.2.2节的分析可知,线性分组码与卷积码游程特征的差异体现在以下两点:(1) 两种编码游程特征的随机性存在差别,卷积码的游程特征更接近于随机序列。(2) 线性分组码和卷积码的游程都随着游程长度的增加呈现递减的特性,但线性分组码的游程特征在信息位长度附近会发生较大的畸变。因此,通过提取游程特征的方式进行编码类型的识别,识别流程如图5所示(Dm如式(3)所示,ri如式(4)所示)。 具体识别步骤如下所示: 步骤1:提取信道编码序列的游程特征xi(i=1,2,…,t),i为游程长度,xi为相应的游程数。 步骤2:利用式(3)计算编码序列游程数与随机序列游程数之间的偏差值 (3) 式中:t为最大游程长度;yi为游程长度为i时的随机序列理论游程数;D0, D1分别为0游程和1游程的偏差值。 图5 识别流程图Fig.5 Identification flowchart 步骤3:计算后一游程与前一游程比值 (4) 步骤4:绘制编码序列与随机序列的游程分布图。 步骤5:由游程分布图和Dm, ri的值判断编码类型。若游程分布图中随机序列与编码序列的分布相近、Dm值小于门限值0.1且ri值大于门限值0.3,判定编码序列采用卷积编码,反之采用线性编码。 3.1 线性分组码的游程检测 为了验证算法的有效性,使用Matlab软件进行仿真实验。随机产生序列长度为33 600比特的(6,3)线性码、(7,4)线性码、(8,4)线性码和(15,5)线性码等4组编码序列,分别提取游程长度从1到10比特的游程数,其游程分布和相应的随机序列游程分布如图6所示,具体的游程数值如表1所示。由图6可以看出,随机序列的游程数走势比较平滑,呈规律性的递减趋势,但线性分组码的游程走势与随机序列出现了较大的分叉。(6,3) 线性码,(7,4)线性码、(8,4)线性码和(15,5)线性码分别在游程长度为2,3,3,4的位置处出现了较大的畸变。从表1的游程数中也得到了与图6相近的结论。线性分组码与随机序列的偏差值在0.41到1.63之间变化。由表1中的数值计算前后游程比值ri,结果如表2所示。 图6 线性分组码游程分布图Fig.6 Run distribution of linear block code 游程长度(6,3)(7,4)(8,4)(15,5)01010101随机理论值1414340564233418141574265425342094200230513106216921472129210820402209210033703691474149715861519112510041050487872142112071858588485255007483676271632626163186179141321231317175183708400912668126131718356561133偏差值Dm1.631.810.390.530.430.440.420.41 表2 线性码游程比值统计 表2中(6,3)线性码、(7, 4)线性码、(8, 4)线性码和(15,5)线性码分别在r2, r3, r3和r4出现最小值0.12, 0.14, 0.12和0.07,与1/2有较大差异。 3.2 卷积码的游程检测 随机产生序列长度为33 600比特的(2,1,6)卷积码、(3,2,2)卷积码、(3,2,[4 3])卷积码和(3,2,[3 2])卷积码等4组编码序列,分别提取游程长度从1到10比特的游程数,其游程分布和相应的随机序列游程分布如图7所示,具体的游程数值如表3所示。由图7可以看出,随着游程长度的增加,4组卷积码与随机序列的游程分布走势基本重合,都呈现出规律性的递减特征。 从表3的游程数中也得到了与图表相近的结论。卷积码与随机序列的偏差值范围在0.03到0.07之间。由表3中的数值计算前后游程比值ri,结果如表4所示。表4中(2,1,6)卷积码、(3,2,2)卷积码、(3,2,[4 3])卷积码和(3,2,[3 2])卷积码的游程比值ri基本稳定在1/2的上下变化。 图7 卷积码游程分布图Fig.7 Run distribution of convolutional code 游程长度(2,1,6)(3,2,2)(3,2,[4,3])(3,2,[3,2])01010101随机理论值13710372137573792378537653768372437002184318031867182918501889190218651850395489895191195194790095292544654684594764394804554784625242243231255251220235239231610115712012312411812511816674566753554635363838382914513727332242偏差值Dm0.050.020.070.060.030.030.030.05 表4 卷积码游程比值统计 3.3 线性分组码与卷积码的游程对比 随机产生序列长度为33 600比特的(6,3)线性码和(3,2,[3 2])卷积码,分别提取游程长度从1到10比特的0游程的游程数,得到两种码字各自的游程分布如图8所示。 图8 线性码与卷积码游程比较图Fig.8 Run comparison of linear block codes and convolutional codes 由图8可以看出,随着游程长度的增加,线性码与卷积码的游程分布虽然都呈现出递减的特征,但两者的走势并不重合。卷积码的游程个数随着游程长度的增加呈现出接近1/2的规律性递减,而线性码的游程数递减并无一定的规律性。从实验结果可知:(1) 与随机序列的游程分布相比,图6中4组编码的游程分布存在明显差异,而图7中4组编码的游程分布与之相近。(2) 实验1中,4组编码的Dm取值在0.41~1.63之间,而实验2中,4组编码的Dm取值在0.03到0.07之间,选择判决门限值D=0.1,实验1的4组偏差值都高于门限、实验2的4组偏差值都低于门限。(3) 实验1中,4组编码的ri取值存在畸变点,而实验2中,4组编码的ri取值都在1/2左右变化,选择判决门限值r=0.3,实验1的4组游程比值都存在低于门限的点、实验2的4组游程比值大部分都高于门限。 因此,根据编码类型的判决准则,实验1中的4组编码为线性分组码,实验2中的4组编码为卷积码,与仿真结果相一致。 3.4 误码性能分析 随机产生序列长度为33 600比特的(6,3)线性码和(3,2,[3 2])卷积码,在误码率为0.01, 0.05, 0.1和0.2的情况下,分别提取游程长度从1到10比特的0游程的游程数,得到两种码字各自的游程分布如图9所示。 图9 误码性能分析Fig.9 Error performance analysis 由图9可以看出,在误码率不断升高的情况下随着游程长度的增加,两种码字的游程分布仍然保持了递减的特征。在误码率为0.01,0.05和0.1时,线性码与卷积码的游程走势有明显的区别,可以较容易地识别出检测序列的编码类型;随着误码率升高到0.2,线性码与卷积码的游程走势呈现出逐渐重合的趋势,但此时两者的游程分布仍然存在差异,可以达到识别编码类型的目的。可见,本文算法具有较好的抗误码性能。 本文利用游程检测的方法,根据线性分组码与卷积码的产生方式不同所导致的编码序列在随机性上的差异,通过统计不同游程长度下,0,1游程数的变化情况,达到对线性分组码和卷积码类型识别的目的。因为游程测试统计的是游程数,在大量的实验数据下,误码导致的有限游程数变化并不会对整体分布产生较大影响,理论分析和仿真实验表明,在误码率一定的情况下,本文算法可以很好地识别出线性分组码与卷积码类型,具有一定的工程应用价值。由于游程长度的选取和最佳判决门限的设置,都会对高效准确的识别起到至关重要的作用,所以有关这方面的研究将会在后续的文章中讨论。 [1] 胡春静, 吴湛击, 李宗艳, 等. 一种速率匹配的准循环LDPC码的编码构造方法[J].南京航空航天大学学报, 2012, 44(1): 93-99. Hu Chunjing, Wu Zhanji, Li Zongyan, et al. Construction of rate-compatible quasi-cyclic LDPC code[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(1): 93-99. [2] 傅婷婷, 吴湛击, 王文博. 基于PEG算法的准循环LDPC码的编码构造方法[J]. 数据采集与处理, 2009, 24(Z1): 182-186. Fu Tingting, Wu Zhanji, Wang Wenbo. PEG-based construction method for Quasi-cyclic LDPC[J]. Journal of Data Acquisition and Processing, 2009, 24(Z1): 182-186. [3] 王平, 朱宏鹏, 李广侠. PEG-GLDPC码设计与性能分析[J]. 数据采集与处理, 2013, 28(3): 358-362. Wang Ping, Zhu Hongpeng, Li Guangxia. Design and performance analysis of PEG-GLDPC[J]. Journal of Data Acquisition and Processing, 2013, 28(3): 358-362. [4] 张仲明, 许拔, 张尔扬. 准循环低密度校验码的快速编码[J].数据采集与处理, 2008, 23(Z1): 105-108. Zhang Zhongming, Xu Ba, Zhang Eryang. Fast encoding of QC-LDPC codes[J]. Journal of Data Acquisition and Processing, 2008, 23(Z1):105-108. [5] 张永光,楼才义. 信道编码及其识别分析[M]. 北京:电子工业出版社,2010: 23-25. Zhang Yongguang, Lou Caiyi. Channel coding and recognition analysis[M]. Beijing: Publishing House of Electronics Industry, 2010: 23-25. [6] 杨晓静,闻年成. 基于码根信息差熵和码根统计的BCH码识别方法[J]. 探测与控制学报, 2010,32(3):69-73. Yang Xiaojing, Wen Niancheng. Recognition method of BCH codes based on roots information dispersion entropy and roots statistic[J]. Journal of Detection & Control, 2010, 32(3): 69-73. [7] 吕喜在,黄芝平,苏绍璟. BCH码生成多项式快速识别方法[J]. 西安电子科技大学学报, 2011,38(6):159-162. Lü Xizai, Huang Zhiping, Su Shaojing. Fast recognition method for generator polynomial of BCH codes[J]. Journal of Xidian University, 2011, 38(6): 159-172. [8] 杨晓炜,甘露. 基于Walsh-Hadamard变换的线性分组码参数盲估计算法[J]. 电子与信息学报, 2012,34(7):1642-1646. Yang Xiaowei, Gan Lu. Blind estimation algorithm of the linear block codes parameters based on WHT[J]. Journal of Electronics & Information Technology, 2012, 34(7): 1642-1646. [9] 解辉,王丰华,黄知涛. 基于改进欧几里德算法的1/2码率卷积码盲识别方法[J]. 电子对抗, 2010(1): 32-36. Xie Hui, Wang Fenghua, Huang Zhitao. A method for blind recognition of 1/2 rate convolution code based on improved euclidean algorithm[J]. Electronic Warfare, 2010(1): 32-36. [10]刘健,王晓君,周希元. 基于Walsh-Hadamard变换的卷积码盲识别[J]. 电子与信息学报, 2010, 32(4): 884-888. Liu Jian, Wang Xiaojun, Zhou Xiyuan. Blind recognition of convolutional coding based on Walsh-Hadamard transform[J]. Journal of Electronics & Information Technology, 2010, 32(4): 884-888. [11]杨小牛. 通信电子战——信息化战争的战场网络杀手[M]. 北京:电子工业出版社,2011: 59-61. Yang Xiaoniu. Communication electronic warfare-killer of battlefield network in information warfare[M]. Beijing: Publishing House of Electronics Industry, 2011: 59-61. [12]刘铭. 线性分组码中的交叠编码迭代译码技术研究[D].成都: 电子科技大学, 2008. Liu Ming. Iterative decoding technology research of linear block code of overlapping coding[D].Chengdu: University of Electronic Science and Technology, 2008. [13]王育民, 李晖,梁传甲. 信息论与编码理论[M].北京:高等教育出版社,2005: 56-59. Wang Yumin, Li Hui, Liang Chuanjia. Information and coding theory[M]. Beijing: Higher Education Press, 2005: 56-59. [14]彭万权. 级联码基于线性叠加反馈的迭代译码研究[D]. 重庆:重庆大学,2005. Peng Wanquan. Study on a iterative decoding of concatenated codes with linear combination feedback[D]. Chongqing: Chongqing University, 2005. [15]朱和贵,张祥德,杨连平,等. 基于人体指纹特征的随机序列发生器[J]. 计算机研究与发展, 2009, 46(11): 1862-1867. Zhu Hegui, Zhang Xiangde, Yang Lianping, et al. Fingerprint-based random sequence generator[J]. Journal of Computer Research and Development, 2009, 46(11): 1862-1867. Blind Identifying of Type of Linear Block Code and Convolutional Code Based on Run Feature Li Xinhao1,2, Zhang Min1,2, Shi Yingchun1,2, Yuan Quan1,2 (1.705 Research Office, Electronic Engineering Institute, Hefei, 230037, China; 2.Key Laboratory of Electronic Restriction, Electronic Engineering Institute, Hefei, 230037, China) Aiming at solving the problem of recognition for the type of linear block code and the convolutional code, a method of the channel coding type recognition based on the run feature is proposed. Namely, the difference of the run feature of the linear block code and convolutional code is analyzed in theory. It shows that the randomness of the convolutional code run feature is superior to that of the linear block code, and the linear block code run number around the information bit length has a certain amount of distortion. Therefore, the code type can be identified by abstracting the run feature of these two codes. Simulation results show that the proposed method has high robustness and accurate recognition, and the method has a certain value in future engineering application. coding identification; linear block code; convolutional code; random; run’s distribution 国家自然科学基金(61171170)资助项目;安徽省自然科学基金青年项目(1408085QF115)资助项目。 2013-09-24; 2014-03-27 TN911.22 A 李歆昊(1989-),男,博士研究生,研究方向:信道编码识别,E-mail: lixinhao1989 616@126.com。 张旻(1966-),男,教授,博士,研究方向:通信信号处理、计算智能。 史英春(1978-),男,博士,研究方向:无线网络。 袁泉(1977-),男,博士,研究方向:无线网络。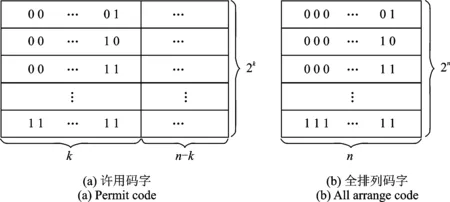

3 仿真实验




4 结束语





