基于时差的宽带相干多辐射源测向算法*

杨 健 刘 渝 狄 慧

(南京航空航天大学电子信息工程学院，南京，210016)



基于时差的宽带相干多辐射源测向算法*

杨 健 刘 渝 狄 慧

(南京航空航天大学电子信息工程学院，南京，210016)

为了防反辐射弹，通常在一定的范围内放置两个或者两个以上的辐射源。该多个辐射源的参数相同，距离也比较靠近。如果运用传统的宽带测向技术，将无法对多个辐射源进行准确测向。针对宽带多辐射源测向问题，本文采用单基线系统，根据两个阵元接收信号谱线共轭相乘产生的新信号谱线结构关系，间接估计出各个辐射源到达两个天线阵元的时差，并通过去直流方法来提高时差估计精度。仿真结果表明，该算法设备简单，在一定条件下测向精度较高。

多辐射源测向；时差；宽带相干信号；单基线；去直流

引 言

现代雷达发射的信号通常都是宽带信号，线性调频(Linear frequency modulation，LFM)是采用最多的调制方式。对于宽带信号，用传统的窄带测向技术已经无法满足其测向精度的要求[1-2]。因此，宽带信号测向是现代雷达和电子对抗中至关重要的技术之一。现有的测向技术中，主要利用信号到达不同阵元的时延估计来实现波达角(Direction of arrival, DOA)估计[3-4]。文献[5]给出了在高信噪比条件下以脉冲包络为观测对象的信号到达时间估计方法，文献[6]研究了矩形包络正弦波脉冲信号的到达时间估计问题，文献[7]提出基于Haar小波到达时间估计方法，文献[8-9]提出基于宽带信号相位谱的分数延时估计方法。但是，这些算法仅能对单信号进行到达时间估计。对于多辐射源的测向，一般采用阵列信号处理方法。文献[10]提出了均匀圆阵相干信源DOA估计的模式平滑算法，文献[11]提出了宽带相干信源DOA估计算法，文献[12]提出了延迟相乘宽带LFM信号阵列测向方法，这些算法需要的设备复杂，要求相干信号的入射角之差比较大。然而，在现代电子对抗中，雷达为了防反辐射弹而设置诱饵，即在一定的范围内放置两个或者两个以上的辐射源。这多个辐射源发射的信号参数相同，即信号的载频、带宽、脉宽和重复周期等相同(即信号相干)，而且方位角非常接近。如果运用传统的阵列信号处理方法，将无法对多个辐射源进行准确测向。

本文基于文献[8]，提出一种单基线宽带信号测向算法，该算法用时延估计来计算出多个辐射源的波达角，从而对多个辐射源进行精确测向。本算法具有设备结构简单，能对多辐射源进行测向并且能够达到较高测向精度的特点。在满足远场条件下，基线距离越大，测向精度越高。仿真实验表明，此方法在一定条件下测向精度较高，可用于对空间多辐射源目标进行精确定位，为精确打击提供支持。

1 单辐射源时差测向原理和估计算法

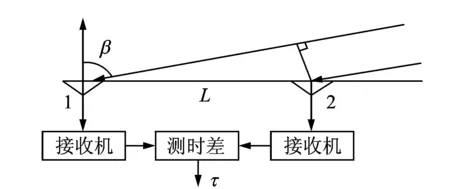
图1 单基线时差测向系统原理图Fig．1 Diagram of direction finding system by single baseline

当辐射源与天线距离满足远场条件时，天线接收到的电磁波可以认为是平面波。图1给出了由两个天线组成的单基线时差测向系统原理图。假设接收到的远场信号与天线阵法线夹角为β，那么到达两个天线1，2之间的时差为

(1)

式中：L为两个天线1，2之间的基线长度；c为电磁波的传播速度。由式(1)可以得到接收信号的波达角

(2)

1.1 辐射源信号模型

假设辐射源发射的信号为LFM信号，经采样后离散序列表达式为

(3)

式中：A为信号的幅度；f为信号的起始频率；N为脉冲宽度内的信号样本点数；k为信号的调频斜率；Δt为采样时间间隔，即Δt=1/fs，fs为采样频率。假设信号带宽为B，那么B=kNΔt=kT，T为脉冲宽度。

假设只有单个辐射源，天线1，2接收到的信号分别为

(4)

式中：τ为辐射源发射的信号到达天线1，2之间的时差；n1(t)，n2(t)为相互独立的复高斯白噪声，其均值为0，方差都为σ2。对式(4)中x1(t)，x2(t)做离散傅里叶变换(Discrete Fourier transform, DFT)，得到频域信号

(5)

式中：S(k)为s(t)的频谱；N1(k)，N2(k)为n1(t)，n2(t)的频谱；D为量化时差，即D=τ/Δt。

将X1(k)与X2(k)共轭相乘得到新的信号

(6)

1.2 基于宽带相位谱的分数延时估计方法

搜索式(6)信号的最高谱线位置，假设搜索到的信号最高谱线位置为K1，然后在[K1-0.5, K1+0.5]区间内做DFT来构造新的谱线值，即

(7)

式中：C为插值率，是一个大于1的正整数。C的取值直接影响到该插值法的精度及复杂度。

(8)

(9)

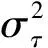
由式(9)可以看出，辐射源信号的波达角估计精度跟输入信号的带宽B，基线长度L，输入信噪比SNRi，信号脉宽N有关系。其中，在基线长度和入射角一定的情况下，波达角估计精度受输入信号的带宽B影响最大，信号的带宽越大，则波达角估计精度越高。

2 多辐射源时差估计算法

2.1 多辐射源模型

本文以两个辐射源为例，并且假设两个辐射源发射的信号除了到达接收天线的时间和初始相位存在差异外，其他参数如信号的调制方式、载频起始频率、带宽、脉宽以及重复周期等完全相同(对于发射方，雷达信号是窄波束，诱饵信号是宽波束；对于电子侦察接收方，均考虑旁瓣接收，各辐射源的接收功率很接近)。

图2 辐射源与天线之间的位置模型图Fig．2 Diagram of location between antennas and sources

在图2中，L为两个天线1,2之间的基线长度，A,B为两个辐射源，d为两个辐射源之间的距离，而且两个辐射源到天线的距离满足远场条件，并假设d≫L。根据图2所示，以天线1的时间为基准，两天线接收到的信号形式为

(10)

2.2 时差估计算法

由于假设两个辐射源发射的信号除了到达接收天线的时间和初始相位存在差异外，其他参数完全相同,那么，以第1个到达的信号为时间基准，则式(10)可写为

(11)

式中：θ为两个信号的初始相位差。对式(11)中x1(t)，x2(t)做DFT变换，得到

(12)

式中：D，D1，D2为量化时差，即D=τ/Δt,D1=τ1/Δt,D2=τ2/Δt。

将X1(k)与X2(k)共轭相乘得到新的信号

(13)

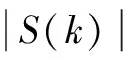
在远场条件下，这两个辐射源的方位角比较接近(一般相差在1°以内)，即量化时差D1,D2比较接近，一般相差一个采样间隔之内，从而导致Y1(k)的谱线图中只有3个谱线峰值，其中量化时差D1,D2所在的谱线峰叠加在一起，无法进行分辨。因此，无法直接通过估计Y1(k)中频率信息来得到时差D1,D2的估计值，只能通过一些运算间接得到它们的估计值。将X1(k)与本身共轭相乘得到新的信号Y2(k)

(14)

(15)

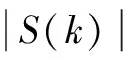
算法1步骤如下：

(1)根据Y1(k)，估计出D1-D和D+D2的值，两个值相加即可计算出D2+D1的值。

(2)根据Y2(k)和Y3(k)，估计出D和D+D2-D1的值，两个值相减即可计算出D2-D1的值。

(3)根据D2-D1和D2+D1的值，可以估计出D1和D2。

算法2步骤如下：

(1)根据Y1(k)，估计出D1-D和D+D2的值。

(2)根据Y2(k)，估计出D的值。

(3)根据D1-D,D+D2和D的值，可以估计出D1和D2。

命题：算法1得到的D1和D2的方差小于算法2得到的D1和D2的方差。

对于算法1：步骤(1)中，由于D2+D1=(D+D2)+(D1-D)，因此D2+D1的方差为

(16)

步骤(2)中，由于D2-D1=(D+D2-D1)-D，因此D2-D1的方差为

(17)

(18)

对于算法2：步骤(3)中，由于D1=(D1-D)+D，D2=(D2+D)-D，因此D1，D2的方差为

(19)

比较式(18，19)可知，算法1得到的D1和D2的方差小于算法2得到的D1和D2的方差，因此采用算法1性能较优。

2.3 信号去直流处理

去直流的关键是估计出信号的直流分量大小，即信号的均值。而由于兔耳效应的存在，Y2(k)时域波形的起始部分和终止部分有抖动，因此必须选取有效的数据段进行处理。Y2(k)波形的截取如图5所示。当把图5中Y2(k)波形有效部分截取出来后，对该段数据进行均值估计，得到直流分量的大小。然后，将该段数据进行去直流后进行频率估计运算。

2.4 算法适用范围与空间角度的关系

在一定条件下，本文算法可以有效地对两个辐射源进行精确测向。但是在某些条件下，该算法的测向精度较差甚至无法进行测向。辐射源与天线的空间关系如图6所示。在图6中，A，B为两个辐射源所在位置，C为天线1所在位置。d为两个辐射源之间的距离，取d=300 m；l为辐射源A到天线1的距离，由于两个辐射源到天线的距离满足远场条件，取l=100 km。θ1，θ2为辐射源A，B发射到C的信号与辐射源阵法线的夹角，称之为轴角。由于l≫d，所以θ1≈θ2。

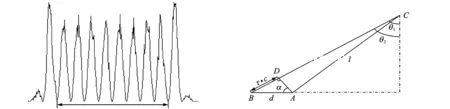
图5 Y2(k)波形的截取示意图 图6 辐射源与天线的空间关系示意图Fig.5 Schematic diagram of waveform interception of Y2(k) Fig.6 Spatial relationship between antenna and radiation sources

取ΔCAD为等腰三角形，其中AC=DC，则BD即为两个辐射源A，B到天线1的距离差。由于θ2-θ1≈0°，因此，∠ADC≈90°，这里做近似直角处理。根据图中的几何关系，可以得到

(20)

因此，两个辐射源到天线1的时差为

(21)

由式(21)可知，两个辐射源到天线1的时间延迟τ受到θ2的影响，θ2越大，时差τ越大。当θ2较小时，得到的τ比较小，比较靠近直流分量。由于受到直流的影响，时差估计误差较大。设采样频率为200 MHz，信号的起始频率为51 MHz，输入信噪比为6 dB，信号长度T=10 μs，信号带宽B=30 MHz，时延τ取值为125，150，175，300，400，500，700 ns，各进行100次蒙特卡洛实验，不同时差条件下时差τ的均方根误差如图7所示。由图7可知，本算法对时差估计的均方根误差受到时差大小的影响。时差越小，越接近直流分量，对其估计的误差就越大。当τ>175 ns，即θ2>10°时，算法性能较好。

3 仿真分析

3.1 去直流对时延估计精度的影响

设采样频率为200 MHz，信号的起始频率为51 MHz，两辐射源的入射角为22.02°，22.95°。输入信噪比为6 dB，信号长度T=10 μs，时差τ=500 ns，信号带宽取10，15，20，30，40，50 MHz，各进行100次蒙特卡洛实验，去直流前后时延估计的性能曲线如图8所示。由图8可知，相比于去直流运算前，进行去直流运算后，时差的均方根误差减小几乎一半。当信号带宽达到15 MHz时，去直流运算后的时差估计均方根误差能达到1ns以内，远远小于采样时间间隔。

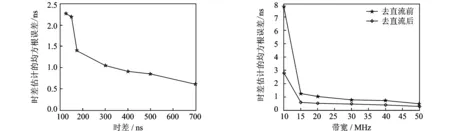
图7 不同时差条件下时差估计性能曲线 图8 去直流前后时差估计性能曲线Fig.7 Estimation precision curve of time-delay on different time-delay Fig.8 Estimation precision curve of time-delay by wiping off direct current

3.2 波达角估计精度与带宽的关系

设输入信噪比为6 dB，信号长度T=10 μs，基线长度L=20 m，信号带宽取10，15，20，30，40和50 MHz，各进行100次蒙特卡洛实验，不同带宽条件下波达角估计的性能曲线如图9所示。由图9可知，波达角估计精度受信号带宽的影响较大，信号的带宽越大，信号的波达角估计精度越高。当信号带宽达到15 MHz以上时，对两个辐射源的波达角估计均方根误差能达到1°以内。

3.3 波达角估计精度与输入信噪比的关系

设信号长度T=10 μs，基线长度L=20 m，信号带宽B=20 MHz，输入信噪比在[5 dB，20 dB]范围内以3 dB为步长，各进行100次蒙特卡洛实验，不同信噪比条件下波达角估计的性能曲线如图10所示。由图10可知，波达角估计精度受输入信号信噪比的影响，信噪比越大，波达角估计精度越高。

3.4 本算法与MUSIC算法比较

设信号长度T=10 μs，基线长度L=20 m，信号带宽B=20 MHz，输入信噪取10 dB，分别采用多路延迟结构的修正MUSIC算法[13]与本文算法，各进行100次蒙特卡洛实验，波达角估计的均方根误差对比如表1所示。由表1可知，由于两个相干辐射源的入射角比较接近，从而导致两个辐射源到两个天线的时差相差较小。此时，采用多路延迟结构的修正MUSIC算法，谱峰分辨率比较低，因而得到的两个辐射源的波达角估计误差较大。但是，本文算法能够对多个位置靠近的相干辐射源进行准确测向，相比于MUSIC算法，测向精度得到大幅度提高。

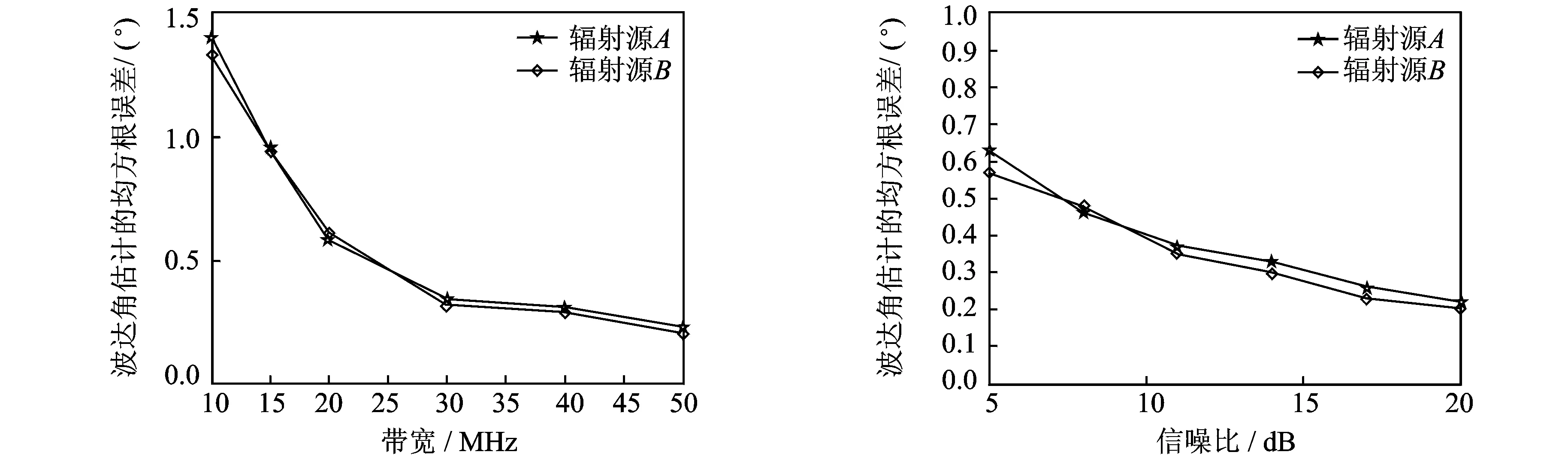
图9 不同带宽条件下辐射源测向性能曲线 图10 不同信噪比条件下辐射源测向性能曲线Fig.9 Direction finding precision on different bandwidth Fig.10 Direction finding precision on different SNR

表1 本文算法与MUSIC算法性能对比表

3.5 非线性调频信号测向性能仿真

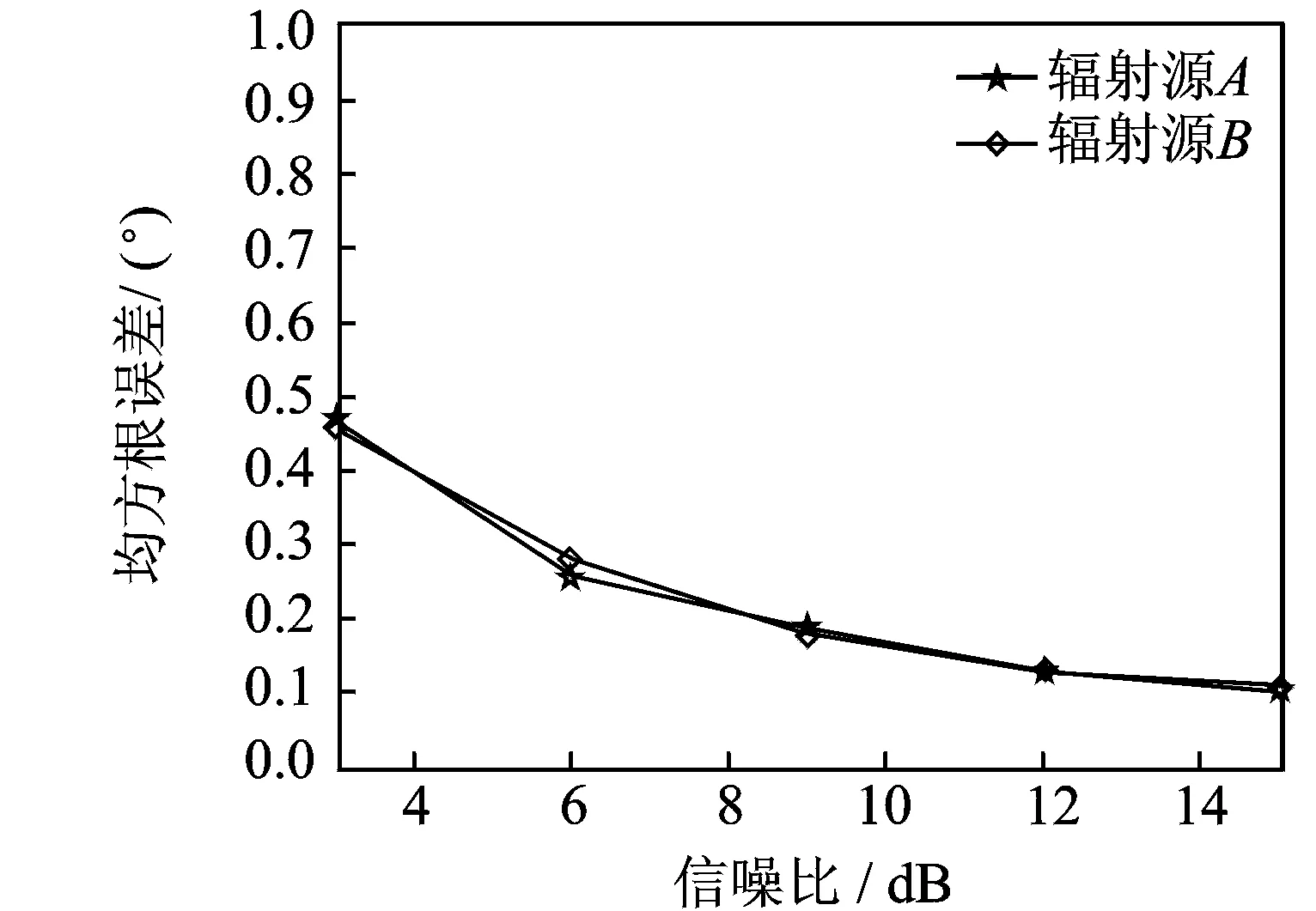
图11 非线性调频信号测向性能曲线 Fig．11 Direction finding precision of nolinear frequency modulated signal

综上所述：当一定的条件下，该算法能够准确地对两个辐射源进行测向。辐射源信号的波达角估计精度跟输入信号的带宽、输入信噪比等有关系。由于Y2(k)，Y3(k)中都存在直流分量，在去除直流分量后，对测向精度有改善。

4 结束语

本文研究了基于时差的长基线宽带多辐射源测向算法。本方法具有结构简单、精度较高等特点，对继续深入研究诱饵信号测向与定位有参考价值。仿真表明，在一定的条件下，本算法能够对多个辐射源进行精确定位，在电子侦察和情报截获等场合具有一定的应用价值。

[1] 赵春晖，李刚，李福昌. 宽带测向研究现状及展望[J].哈尔滨工程大学学报，2006，27(2)：290-295.

Zhao Chunhui, Li Gang, Li Fuchang. Research and development of wide-band direction finding[J]. Journal of Harbin Engineering University,2006,27(2):290-295.

[2] 刘思沉. 短波宽带测向算法研究及其实现[D].西安：西安电子科技大学，2010.

Liu Sichen. Research and implementation of shortwave wideband DF algorithm[D]. Xi′an: Xidian University, 2010.

[3] 尤国红，邱天爽，兰天. 脉冲噪声环境下宽带循环平稳信号DOA估计算法[J].数据采集与处理，2012,27(4):399-403.

You Guohong, Qiu Tianshuang, Lan Tian. DOA estimation algorithm of wideband cyclostationary signals in impulsive noise environment[J]. Journal of Data Acquisition and Processing, 2012,27(4):399-403.

[4] 张刚兵，刘渝，刘宗敏. 基线比值法相位解模糊算法[J].南京航空航天大学学报，2008, 40(5):665-669.

Zhang Gangbing, Liu Yu, Liu Zongmin. Unwrapping phase ambiguity algorithm based on baseline ratio[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2008, 40(5):665-669.

[5] Ho K C, Chan Y T, Inkol R. Pulse arrival time estimation based on pulse sample ratios [J]. IEEE Proceeding of Radar Sonar and Navigation, 1995,142(4) : 153-157.

[6] Chan Y T, Lee B H, Inkol R, et al. Detection and arrival time estimation of a pulsed sinusoid [C]∥Communications, Computers and signal Processing. PACRIM: IEEE, 2005: 37-40.

[7] 胡国兵，刘渝，邓振淼. 基于Haar小波变换的信号到达时间估计[J].系统工程与电子技术，2009， 31(7)：1615-1619.

Hu Guobing, Liu Yu, Deng Zhenmiao. Arrival time estimation of signals based on Haar wavelets transform[J]. Systems Engineering and Electronics, 2009, 31(7):1615-1619.

[8] Bai Yechao, Zhang Xinggan, Tang Lan. Subsample time delay estimation based on phase spectrum of band limited stochastic signals[J]. Transactions of Nanjing University of Aeronautics & Astronautics,2010, 27(2):170-175.

[9] 杨健，刘渝，狄慧. 基于时差校正的长基线宽带测向算法[J].系统工程与电子技术，2013，35(1)：20-28.

Yang Jian, Liu Yu, Di Hui. Long baseline direction finding algorithm of wideband signal based on time-delay correction[J]. Systems Engineering and Electronics, 2013，35(1)：20-28.

[10]马常霖，彭应宁，田立生，等. 均匀圆阵相干信源DOA估计的模式平滑算法[J].电子科学学刊，1998，20(1)：14-19.

Ma Changlin, Peng Yingning, Tian Lisheng, et al. Mode space smoothing algorithm for DOA estimation of coherent sources with uniform circular array[J]. Journal of Electronics, 1998,20(1):14-19.

[11]张润生，谢锘，张建立. 宽带相干信源DOA估计算法[J]. 无线电工程，2010，40(10)：16-19.

Zhang Runsheng, Xie Nuo, Zhang Jianli. DOA estimation algorithm for wideband coherent Sources[J]. Radio Engineering, 2010,40(10):16-19.

[12]黄知涛，刘章孟，周一宇. 延迟相乘宽带LFM信号阵列测向方法[J].电子学报，2009，37(7)：1606-1613.

Huang Zhitao, Liu Zhangmeng, Zhou Yiyu. A new direction-of-arrival estimation method for wideband LFM sources based on temporal delay-and-product [J]. Acta Electronica Sinica, 2009,37(7):1606-1613.

[13]王鑫, 赵春晖, 戎建刚. 多路延迟结构的修正MUSIC 算法频率估计[J]. 系统工程与电子技术, 2009, 31(4): 795-798.

Wang Xin, Zhao Chunhui, Rong Jiangang. Frequency estimation of modified MUSIC algorithm based on multi-path delay structure[J]. Systems Engineering and Electronics, 2009, 31(4): 795-798.

[14]Varshney L R, Thomas D. Sidelobe reduction for matched filter range processing[C]//IEEE Radar Conference. Huntsville: IEEE, 2003:446-451.

[15]Skolnik M I. Radar Handbook [M]. Third Edition.New York: McGraw-Hill, 2008.

Multiple Radiation Sources Direction Finding Algorithm of Wideband Coherent Signal Based on Time-Delay

Yang Jian, Liu Yu, Di Hui

(College of Electronics and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016,China)

In the area of modern electronic warfare, two or more radiation sources are always placed within a certain range to prevent the attack from anti-radiation missile. These radiation sources are placed closely and their parameters are identical. In the case of multiple radiation sources, traditional direction finding algorithms of wideband signal cannot achieve good direction finding precision. Therefore, the single baseline system is set. New signals are created by the conjugate multiplication of signal spectrums received by two antenna array. According to the spectrum structure relationship of new signals, the time-delay estimation of radiation sources can be obtained indirectly. And the precision of the time-delay can be improved by wiping off the direct current component. The method has the feature of simple equipment. Simulation results show that the algorithm has good direction finding precision under certain conditions.

multiple radiation sources direction finding; time-delay; wideband coherent signal; single baseline；direct current wiping-off

国家自然科学基金(61201208)资助项目；江苏高校优势学科建设工程资助项目；南京航空航天大学基本科研业务费专项科研(NN2012068)资助项目。

2013-04-16；

2013-09-19

TN971

A

杨健(1986-)，男，博士研究生，研究方向：雷达信号处理、电子侦察,E-mail:james200586@163.com。

刘渝(1945-)，男，教授，博士生导师，研究方向：雷达信号处理、电子侦察。

狄慧(1986-)，女，博士研究生，研究方向：雷达信号处理、电子侦察。