基于改进逻辑回归分类算法的LSB匹配隐写检测*

郭继昌 季文驰 顾翔元

(天津大学电子信息工程学院，天津,300072)



基于改进逻辑回归分类算法的LSB匹配隐写检测*

郭继昌 季文驰 顾翔元

(天津大学电子信息工程学院，天津,300072)

常见的采用高斯核支持向量机(Gaussian support vector machine, G-SVM)分类算法构建分类器的隐写检测方法对最低比特位(Least significant bit, LSB)匹配隐写算法均存在训练时间过长的问题。针对这一问题，提出一种改进逻辑回归分类算法，即L曲线截断正则化迭代重加权最小二乘(L-curve truncated-regularized iteratively re-weighted least squares, LTR-IRLS)算法。该算法采用L曲线法来确定适合于隐写特征的Tikhonov正则算法的近似最优参数，并通过实验寻找出符合隐写特征的截断牛顿算法收敛参数，从而提高了检测准确率；采用重加权最小二乘法计算最大似然估计，并通过截断牛顿法避免计算最小二乘中的海森矩阵，降低了计算量。理论分析与实验结果证明，针对LSB匹配隐写检测，LTR-IRLS分类算法在保证检测准确率优于G-SVM分类算法的情况下，极大地降低了训练时间，从而提高了检测速度。

L曲线法； 迭代重加权最小二乘； 截断牛顿法； 隐写检测； LSB匹配

引 言

隐写检测的目的是检测出使用了隐写算法隐藏信息的载体[1-2]。最低比特位(Least significant bit，LSB)匹配隐写检测就是针对LSB匹配隐写算法而研究的一种隐写检测方法。LSB匹配隐写算法是一种将隐写信息隐藏在载体图像最低比特位上，从而使隐写信息类似于噪声的算法。它对载体影响很小，简单通用，大部分多媒体文件(如图像和视频文件等)都可作为其载体，因此如何准确而快速地检测LSB匹配隐写算法已成为隐写检测领域的一个重要课题[3-4]。为检测出LSB匹配隐写算法隐写过的载体图像，Ker等从图像的小波域中提取出小波绝对矩(Wavelet absolute moments，WAM)作为隐写特征，结合支持向量机(Support vector machine，SVM)分类算法提出了WAM隐写检测算法[5]。Pevny等根据图像相邻像素的相关性，以相邻矩阵差值(Subtractive pixel adjacency matrix，SPAM)作为隐写特征，并结合高斯核支持向量机(Gaussian SVM，G-SVM)分类算法提出了SPAM隐写检测算法[6]。钟尚平等以LSB序列短重码间距统计变量之间的相关性作为隐写特征，将混合高斯模型和G-SVM算法融合，提出了一种基于LSB序列局部特征的隐写检测算法[7]。以上3种算法虽然都具有较高的隐写检测准确率，但其采用的SVM和G-SVM分类算法的训练时间过长，严重影响了隐写检测速度[8-10]。为了提高隐写检测速度，学者们在分类算法的选择和改进上开展了研究。Holub等针对所有隐写方法提出了通用的集成分类隐写检测方法[11]。该方法虽然检测速度大幅提高，但因其未对LSB匹配隐写算法做出针对性改进，检测准确率较使用G-SVM分类算法的检测方法有所降低。Lubenko等尝试采用逻辑回归算法(Logistic regression，LR)作为分类算法[12]，其方法在检测准确率与使用G-SVM算法相当的情况下，检测速度提升了约12%，成为比之前方法都优秀的LSB匹配隐写检测方法。因此，对LR算法进行改进并以此构建分类器成为了一个值得研究的方向。

截断正则化迭代重加权最小二乘(Truncated-regularized iteratively re-weighted least squares，TR-IRLS)算法是一种快速逻辑回归算法[13-14]，它将截断牛顿算法、正则化和迭代重加权最小二乘(Iteratively re-weighted least squares，IRLS)等方法相结合，在保证分类准确率与LR和G-SVM等算法相当的同时，训练时间有明显提升[13]。但TR-IRLS算法的参数固定，在Tikhonov正则化时，未考虑如何寻找近似最优参数，在截断牛顿收敛时也并未考虑收敛截止参数的敏感性，所以并不能直接应用于隐写检测中。本文对TR-IRLS算法进行了改进，提出了一种改进逻辑回归分类算法，即L曲线截断正则化迭代重加权最小二乘(L-curve TR-IRLS，LTR-IRLS)算法。该算法采用L曲线法来确定适合于隐写特征的Tikhonov正则算法的近似最优参数，并通过实验寻找出符合隐写特征的截断牛顿算法收敛参数，从而提高了检测准确度；采用重加权最小二乘法计算最大似然估计，并通过截断牛顿法避免计算最小二乘中的海森矩阵，从而大大降低了计算量。实验结果表明， LTR-IRLS分类算法在保证检测准确率优于G-SVM等通用分类算法的情况下，极大地降低了训练时间，从而提高了检测速度，适合应用于LSB匹配隐写检测中。

1 LTR-IRLS分类算法

LTR-IRLS算法是在TR-IRLS算法的基础上，针对LSB匹配隐写算法而改进的一种分类算法。其中利用TR-IRLS分类算法构造TR-IRLS分类器并实现隐写检测的过程如下。

1.1 TR-IRLS分类器的构造及其隐写检测过程

TR-IRLS是一种快速逻辑回归算法，该算法可快速计算出样本的回归系数[14]，用TR-IRLS算法构建分类器可分为训练和测试两个阶段，TR-IRLS分类器如图1所示。

图1 TR-IRLS分类器Fig.1 TR-IRLS classifier

1.1.1 训练阶段

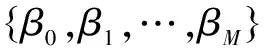
(1) 使用一个R行M列的训练特征矩阵X，矩阵每行代表一个样本xi，每列代表样本的一维特征。Y是含有R个yi元素的标记列向量，用来标记对应训练特征样本的正负，其中Y的元素为0时对应的样本为负样本，即未隐写图像，为1时对应样本为正样本，即隐写图像。

(2) 通过逻辑斯特方程建立训练特征矩阵X与标记列向量Y关系的模型，逻辑斯特方程为

(1)

式中：β为逻辑回归系数; μ为预测概率;xi代表第i行的特征。

(3) 用似然函数表示逻辑回归的损失函数，得到的最大似然方程为

(2)

(4) 采用Tikhonov算法对似然方程进行正则化，并使用IRLS法迭代计算其最大似然估计，得到逻辑回归系数。

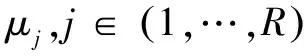
(3)

(4)

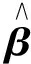
(5)

1.1.2 测试阶段

输入测试特征向量xi，将测试特征与逻辑回归系数对应相乘并相加，表达式为

(6)

对式(6)的结果进行sigmoid变换[14]，表达式为

(7)

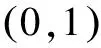
TR-IRLS算法可在保证准确率的条件下，对样本进行快速分类。但算法并未给出Tikhonov正则化时参数的选择方法，而是使用了固定的参数10[14]。在LSB匹配隐写检测中由于隐写特征的特殊性，TR-IRLS算法并不能直接用于LSB匹配隐写检测。因此，本文提出了使用L曲线法计算出适于LSB匹配隐写检测的Tikhonov参数的方法。

1.2 L曲线法计算Tikhonov正则算法的最优参数

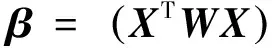
(8)

式中：I为单位矩阵。

图2 L曲线图Fig.2 L-curve diagram

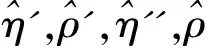
(9)

表1 L曲线选取参数与固定参数的准确率对比

1.3 截断牛顿法在隐写检测中优化参数的选择

在RLS计算重加权的循环过程中，式(10)是计算难点，它是有M个变量和等式的线性方程组。其中，权重W在每次迭代时都会重新计算，花费大量时间。为解决此问题，TR-IRLS使用截断牛顿法求解式，如下式所示

(10)

截断牛顿法克服了原本牛顿法计算量大的缺点，它的基本思想是在迭代过程中，利用函数在迭代点的梯度方向以及前一次搜索方向，构造一个与前面搜索方向共轭的新的搜索方向，作为当前的迭代方向，如式(11)所示。同时，为保证算法的收敛性，截断牛顿法提出了使用相对残差作为结束迭代的收敛准则，即“截断”牛顿方程求解的终止条件，如式(12)所示。

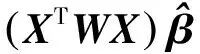
输出：Av=b

初始化：迭代次数i=0，初始化允许误差r0=b-Av0

循环：

(1) 更新搜索方向的参数τi：

在零次迭代时：τi=0

(2) 更新搜索方向：di=ri+τidi-1

(11)

(4)计算新的解：vi+1=vi-αidi

(5) 计算新的允许误差：ri+1=b-Avi

(6) i=i+1

(12)

与其他最优化算法相同，截断牛顿法对收敛参数的选择十分敏感，收敛参数的选择直接影响检测准确率。所以，将LTR-IRLS算法应用于隐写检测中时，选择合适的收敛参数十分关键。本文分别从图像库中选取1 000幅，3 000幅以及5 000幅3种不同数量级的3组嵌入率为0.5的隐写图像，在α=10的条件下进行对比试验，结果如表2所示。检测准确率随收敛参数的变化规律如图3所示，其中横坐标为收敛参数的取值，纵坐标为检测准确率。由图3可知，对于不同数量级的训练特征集，检测准确率都随着收敛参数ε取值的增加，先上升而后快速下降，呈现凸型曲线，且在ε=10-4和ε=10-5的区间内，检测准确率普遍最高，故本文选取收敛参数ε=5×10-5。

表2 不同收敛参数对应的最高准确率

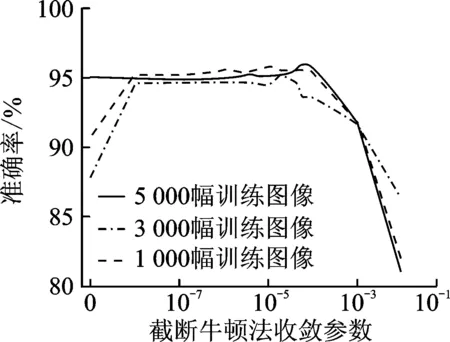
图3 准确率与收敛参数关系图Fig.3 Relation between accuracy and convergence parameter

2 隐写特征提取

本文使用的隐写特征是针对空域隐写提出的SPAM隐写特征[16-17]，其原理是利用二阶马尔可夫链对图像的相邻像素进行建模，并将图像转移概率矩阵的子集作为特征[18]。马尔可夫链的阶数和相邻像素差值T共同决定了模型的维数。其过程如下。假设一幅m×n个像素点的灰度图像素点表示为Ii,j，其中Ii,j∈{0,1,2,…,255}, i∈{1,…,m},j∈{1,…,n}。首先计算8个方向上的差值和转移概率，以水平方向为例，8个方向分别用{←, →, ↓, ↑, ↖, ↘, ↙, ↗}8个特殊符号标记。

(1) 首先计算相邻像素的差值矩阵D

(13)

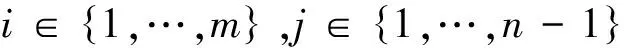
(2) 计算水平方向的马尔可夫转移概率

一阶马尔可夫转移概率表达式如下

(14)

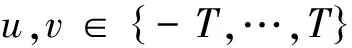
二阶马尔可夫转移概率表达式如下

(15)

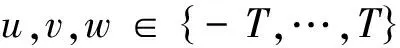
(3) 为降低特征维度，根据空域自然图像统计特征镜像对称的特征，计算得到水平方向、垂直方向和对角线方向特征的平均值，组成新特征集

(16)

特征集维度的计算公式为k=2(2T+1)3，其中T=3，所以SPAM特征共有 686维[5]。

3 实验与分析

针对不同数量的训练图像，本文共进行了两个实验，对比了采用LTR-IRLS， G-SVM， Ensemble和LR四种不同分类算法时隐写检测的性能。其中，G-SVM使用网格搜索的方法计算最优参数[19]。实验评价标准为检测准确率、检测算法所得分类器的训练时间和接收者操作特征曲线(Receiver operating characteristic curve，ROC)。其中检测准确率的计算公式为

(17)

式中：PFp和PFn分别代表误报率(将未隐写图像误检测为隐写图像)和误否认率(将隐写图像误检测为未隐写图像)。

ROC曲线图表示隐写检测的性能。其横轴为错误命中率(False positive rate，FPR)，代表将未隐写图像误检测为隐写图像的概率；纵轴为命中率(True positive rate，TPR)，代表将隐写图像正确分类为隐写图像的概率。曲线下的面积越大，隐写检测算法性能越好。

本文实验与文献[6,20]中的实验作对比，使用的图像库为包含10 000幅512像素×512像素的JPEG格式灰度图像的BOWS2图像库[21]，图像的主题包括场景、人物及植物等。实验在LINUX环境，计算机配置为Core 2 Duo 2.53 GHz CPU，2 GB RAM的条件下进行。

实验1从图像库中随机挑选6 000幅图像，按嵌入率为0.25, 0.5位/像素两种比例分别对原始图像进行LSB匹配隐写，得到不同嵌入率的隐写和未隐写图像6 000对。将所得图像等分两组，其中一组3 000对用于训练，另外一组用于测试。计算可得本组训练特征的Tikhonov近似最优参数α=1.961 5，且截断牛顿算法的收敛参数ε=5×10-5。从表3所示的实验结果可以看出，与其他3种分类算法相比，在检测准确率上，本文提出的LTR-IRLS分类算法有0.2%～1.1%的提升；在训练时间上，采用G-SVM和LR分类算法的训练时间分别约为6 h和5 h，采用Ensemble也需要约1.5 min的时间，而采用LTR-IRLS分类算法的训练时间仅为7 s左右，有了量级上的提升，极大地提高了检测速度。

表3 不同嵌入率下4种分类算法的准确率和训练时间

图4为嵌入率分别为0.25， 0.5位/像素时使用LTR-IRLS,G-SVM,LR和Ensemble四种分类算法的隐写检测ROC曲线。从图中可以看出，在嵌入率为0.25位/像素时，使用LTR-IRLS分类算法的隐写检测性能优于其余3种分类算法。并且随着嵌入率的增加，LTR-IRLS分类算法的性能优势越发明显。

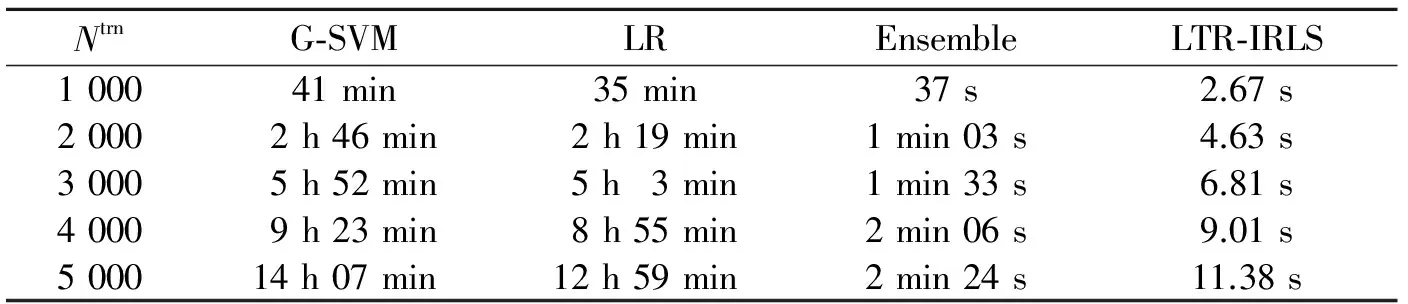
实验2为从图像库中随机选择了不同数量的训练图像，在嵌入率为0.25位/像素的情况下对使用4种分类算法的检测时间进行对比，如表4所示。可以看出，虽然4种分类算法的训练时间均随着训练图像的数量线性增加，但本文提出的LTR-IRLS算法的训练时间始终是秒级的，与其他3种分类算法的小时级相比，有了量级上的提升，从而极大提高了整体隐写检测速度。Ntrn代表训练图像个数。

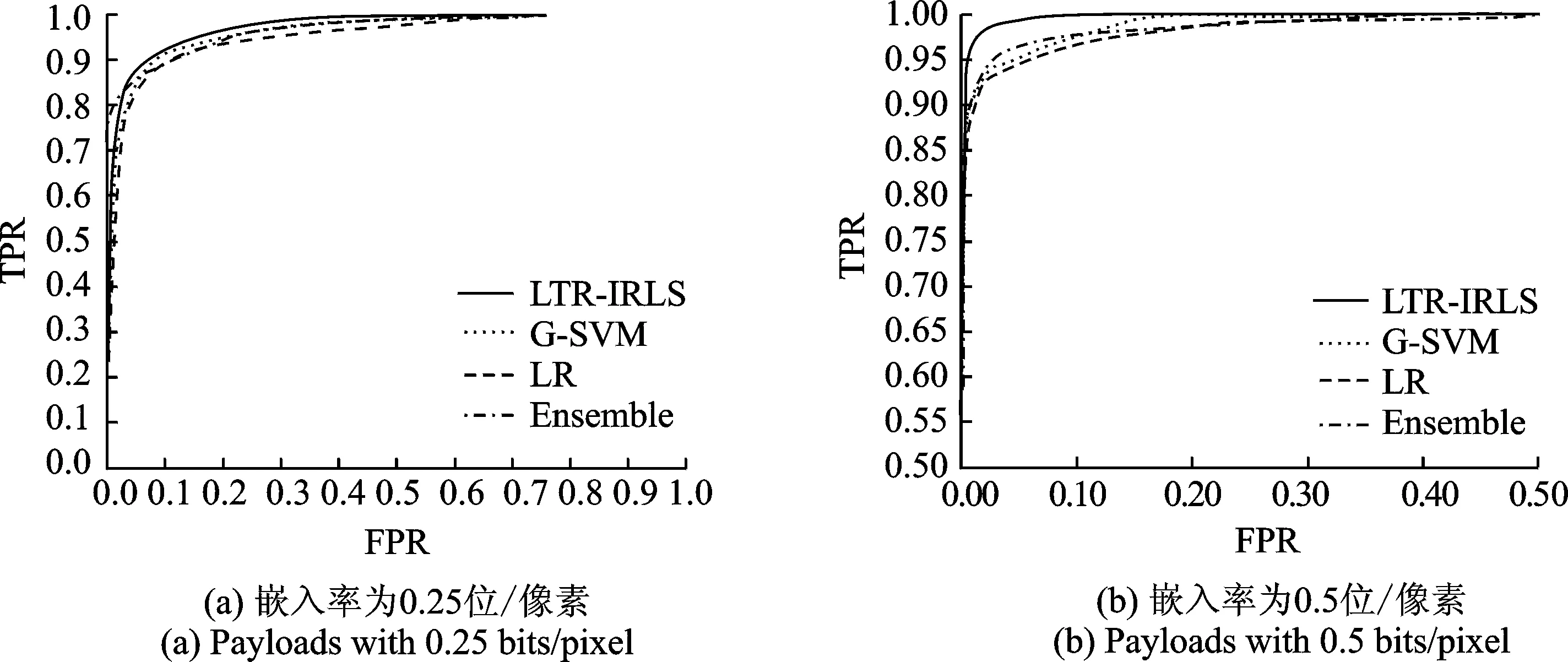
图4 4种分类算法的ROC曲线对比Fig.4 Comparison of ROC curves using four classification algorithms

NtrnG⁃SVMLREnsembleLTR⁃IRLS100041min35min37s2．67s20002h46min2h19min1min03s4．63s30005h52min5h3min1min33s6．81s40009h23min8h55min2min06s9．01s500014h07min12h59min2min24s11．38s

4 结束语

本文针对采用LSB匹配的隐写检测算法，从提高其检测准确率和检测速度的角度出发，基于TR-IRLS算法和L曲线法，提出了一种适合于空域LSB匹配隐写特征的LTR-IRLS分类算法，并对LTR-IRLS算法原理进行了阐述。与已有的LSB匹配隐写检测分类算法相比，本文算法在检测准确率提升0.2%～1.1%的同时，训练时间有了量级上的减少，从而极大地提高了检测速度，与之前的算法相比实用性明显增强。然而，本文所使用的SPAM空域隐写特征在隐写信息嵌入率较低的情况下存在一定的误检率和漏检率。因此，如何设计一种和逻辑回归更加匹配的空域隐写特征提取方法将成为下一步研究的方向。

[1] Lou D C，Hu C H.LSB steganographic method based on reversible histogram transformation function for resisting statistical steganalysis[J].Information Sciences，2012，188(2)：346-358.

[2] Ker A D，Bas P，Bohme R，et al.Moving steganography and steganalysis from the laboratory into the real world[C] ∥ Proceedings of the First ACM Workshop on Information Hiding and Multimedia Security.Portland：ACM，2013：45-58.

[3] 刘学谦，平西建，张涛，等.基于滤波复原的小波特征LSB匹配隐写分析方法[J].数据采集与处理，2010，25(4)：749-756.

Liu Xueqian，Ping Xijian，Zhang Tao，et al.Steganalysis of LSB matching based on wavelet feature of filtering restoration[J].Journal of Data Acquisition and Processing，2010，25(4)：749-756.

[4] Fridrich J，Kodovsky J.Steganalysis of LSB replacement using parity-aware features[C] ∥ Information Hiding.Heidelberg, Berlin：Springer,2013：31-45.

[5] Ker A D，Lubenko I.Feature reduction and payload location with WAM steganalysis[C] ∥ IS&T / SPIE Electronic Imaging.San Diego：International Society for Optics and Photonics，2009：72540A-72540A-13.

[6] Pevny T，Bas P，Fridrich J.Steganalysis by subtractive pixel adjacency matrix[J].Information Forensics and Security，IEEE Transactions on，2010，5(2)：215-224.

[7] 钟尚平，徐巧芬，陈羽中，等.一种基于LSB序列局部特征的通用隐写检测方法[J].电子学报，2013，41(2)：239-239.

Zhong Shangping，Xu Qiaofen，Chen Yuzhong，et al.A universal steganalysis method based on local features extracted from LSB sequences[J].Acta Electronica Sinica，2013，41(2)：239-239.

[8] 杨林聪，夏志华.针对空域LSB匹配的隐藏信息检测方法[J].中南大学学报：自然科学版，2013，44(2)：182-191.

Yang Lincong，Xia Zhihua.Steganalytic method based on spatial LSB matching[J].Journal of Central South University：Science and Technology，2013，44(2)：182-191.

[9] 刘新平，薛希文.基于改进LS-SVM的随钻测量数据传输误码率预测[J].数据采集与处理，2014，29(5)：790-794.

Liu Xinping，Xue Xiwen.Prediction of error rate in measurement-while-drilling data transmission based on improved LS-SVM method[J].Journal of Data Acquisition and Processing，2014，29(5)：790-794.

[10]万宝吉，张涛，李文祥，等.基于多分类器融合的未知嵌入率图像隐写分析方法[J].数据采集与处理，2014，29(5)：749-756.

Wan Baoji，Zhang Tao，Li Wenxiang，et al.Multi-classifier fusion based rate-unknown image steganalysis[J].Journal of Data Acquisition and Processing，2014，29(5)：749-756.

[11]Holub V，Fridrich J，Denemark T.Random projections of residuals as an alternative to co-occurrences in steganalysis[C] ∥ IS&T / SPIE Electronic Imaging.San Diego：International Society for Optics and Photonics，2013：11.

[12]Lubenko I，Ker A D.Steganalysis using logistic regression[C] ∥ IS&T / SPIE Electronic Imaging.San Diego：International Society for Optics and Photonics，2011：11.

[13]Zhu J，Hastie T.Kernel logistic regression and the import vector machine[J].Journal of Computational and Graphical Statistics，2005，14(1)：171-180.

[14]Komarek P，Moore A W.Making logistic regression a core data mining tool with TR-IRLS[C] ∥ Fifth IEEE International Conference on Data Mining.Piscataway：IEEE，2005：4.

[15]Dembo R S，Steihaug T.Truncated-newtono algorithms for large-scale unconstrained optimization[J].Mathematical Programming，1983，26(2)：190-212.

[16]Holub V，Fridrich J.Random projections of residuals for digital image steganalysis[J].Information Forensics and Security，IEEE Transactions on，2013，8(12)：1996-2006.

[17]张昊，平西建.Markov隐写检测特征的一种新设计[J].电子与信息学报，2013，35(8)：1907-1913.

Zhang Hao，Ping Xijian.New design of markov steganalytic features [J].Journal of Electronics & Information Technology，2013，35(8)： 1907-1913.

[18]孙怡峰，刘粉林.Gauss-Markov载体下扩频隐写的抗检测性能分析[J].数据采集与处理，2010，25(4)：462-468.

Sun Yifeng，Liu Fenlin.Security of spread-spectrum stegnaography for Gauss-Markov covers[J].Journal of Data Acquisition and Processing，2010，25(4)：462-468.

[19]刘绍毓，周杰，李弼程，等.基于多分类SVM-KNN的实体关系抽取方法[J].数据采集与处理，2015，30(1)：202-210.

Liu Shaoyu，Zhou Jie，Li Bicheng，et al.Entity relation extraction method based on multi-SVM-KNN classifier[J].Journal of Data Acquisition and Processing，2015，30(1)：202-210.

[20]Torkaman A，Safabakhsh R.A fast and accurate steganalysis using ensemble classifiers[C] ∥ Machine Vision and Image Processing (MVIP)，2013 8th Iranian Conference on，2013：22-26.

[21]Bas P，Furon T.BOWS-2 [EB/OL].http:∥bows2.ec-lille.fr, 2007-07-10.

Steganalysis of LSB Matching Based on Improved Logistic Regression Algorithm

Guo Jichang, Ji Wenchi, Gu Xiangyuan

(School of Electronic Information Engineering, Tianjin University, Tianjin, 300072, China)

Least significant bit (LSB) matching algorithm and common steganographic methods, which use Gaussian support vector machine (G-SVM) algorithm as the classifier, spend too much training time. Therefore, an improved logistic regression classifying algorithm named L-curve truncated-regularized iteratively re-weighted least squares(LTR-IRLS) is proposed. Firstly, near-optimal parameters of Tikhonov regularization are determined based on L-curve, and convergence parameters of the truncated Newton algorithm are obtained through experiments for increasing the detection accuracy. Secondly, iteratively re-weighted least squares are utilized to search for the maximum loss expectancy and truncated Newton methods are utilized to avoid computing the Hessian matrix in the objective function, therefore reducing the computation amount greatly. Theoretical analysis and experimental results verify that LTR-IRLS can ensure the detection accuracy rate higher than G-SVM classifier, meanwhile reducing the training time and increaseing the detection speed.

L-curve; iteratively re-weighted least squares (IRLS); truncated Newton methods; steganalysis; least significant bit (LSB) matching

天津市自然科学基金(15JCYBJC15500)资助项目。

2015-07-28;

2015-11-05

TP391

A

郭继昌(1966-)，男，教授，研究方向：数字图像处理、语音信号处理，E-mail:jcguo@tju.edu.cn。

季文驰(1989-)，男，硕士研究生，研究方向：模式识别、图像隐写分析。

顾翔元(1989-)，男，硕士研究生，研究方向：图像隐写分析。