往复式冰箱压缩机曲轴动态特性与轴承润滑计算分析

吴建华,雷源,王刚,杨骅,陆龙泉

(1.西安交通大学能源与动力工程学院,710049,西安;2.加西贝拉压缩机有限公司,314006,浙江嘉兴)



往复式冰箱压缩机曲轴动态特性与轴承润滑计算分析

吴建华1,雷源1,王刚1,杨骅2,陆龙泉2

(1.西安交通大学能源与动力工程学院,710049,西安;2.加西贝拉压缩机有限公司,314006,浙江嘉兴)

提出一种往复式冰箱压缩机受动态载荷作用的悬臂曲轴动态特性及其主副滑动轴承油膜厚度的计算分析方法。采用压缩机汽缸内压力变化实测数据,考虑活塞、连杆与曲轴所受气体力和惯性力,建立了曲轴与电机转子横向位移与倾斜动力学方程;采用滑动轴承有限长油膜模型,并用有限元离散化方法数值逼近;观测了过负荷工况寿命试验后曲轴磨损情况,测量了曲轴圆度。对样机的计算分析结果表明:压缩机工作时,曲轴除转动与平移外,倾斜方位也在不断变化,但上部中心基本上在第一象限内,而下部在第三象限,转角为0°时曲轴倾斜最大;额定与过负荷工况下,曲轴与轴承孔上部会发生偏磨,而轴承与轴承孔下端过负荷工况会发生偏磨;增加曲轴直径,主副轴承最大偏心率都会减少,最小油膜厚度明显增加;转速增大会使主轴承油膜厚度减小,而副轴承油膜厚度增加。该结果可为节能环保冰箱压缩机的研发提供参考。

往复式冰箱压缩机;曲轴;轴承;润滑

符号表

B轴承宽度,m

C轴承间隙,m

F力,N

h油膜厚度,m

I转动惯量,kg·m2

M力矩,N·m

m质量,kg

L长度,m

p压力,Pa

R半径,m

α曲轴倾斜角,rad

β连杆与汽缸轴线夹角,rad

θ曲轴转角,rad

τ连杆比

μ动力黏度,Pa·s

ω角速度,rad/s

下标

1 主轴承

2 副轴承

b 平衡重或轴承

c 连杆

g 气体

j 轴颈

p 活塞

xx轴

yy轴

o 油膜

s 曲轴或曲轴与电机

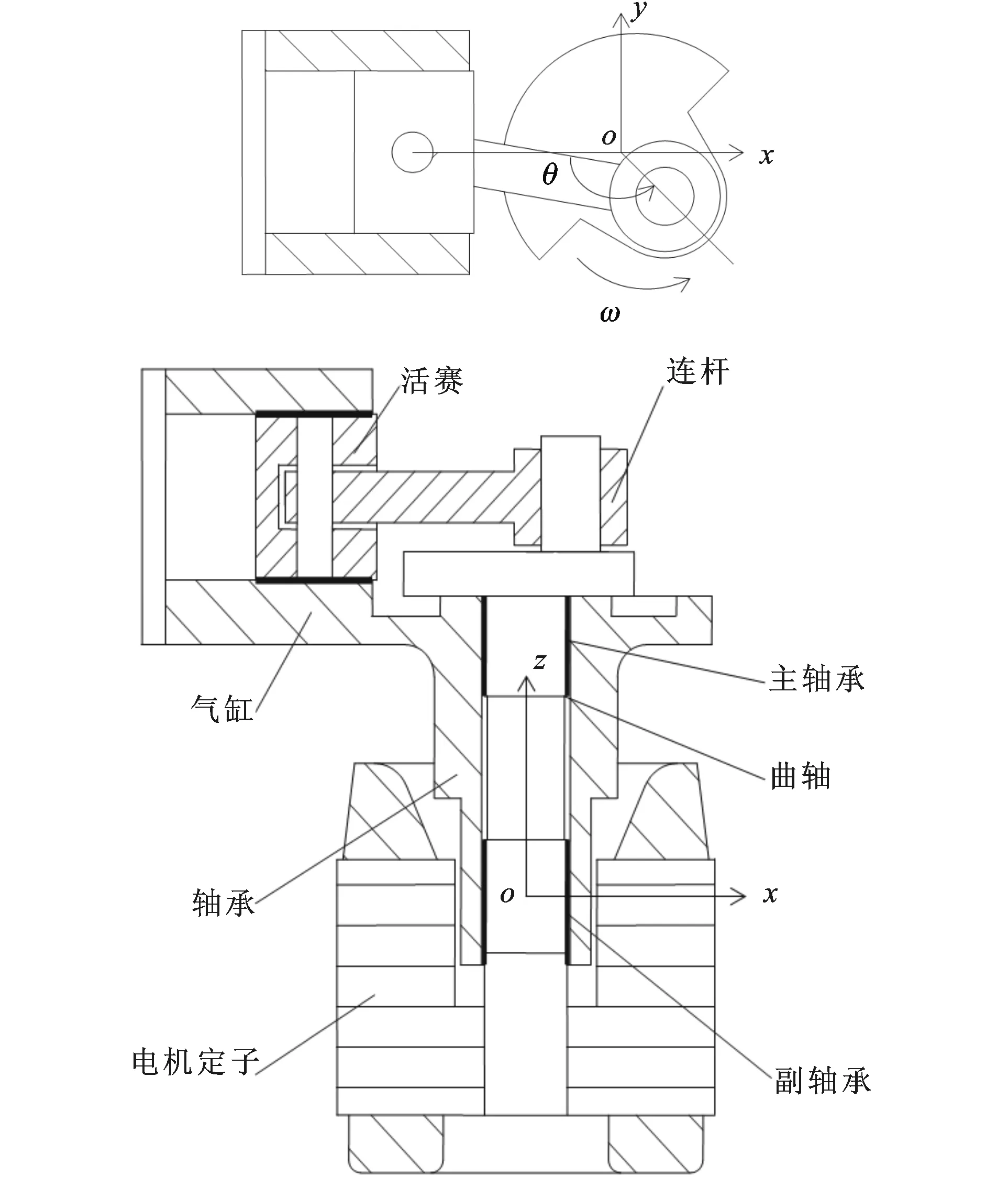
图1 冰箱压缩机运动机构与曲轴坐标系

冰箱压缩机驱动连杆与活塞运动的曲轴是由两个滑动轴承支撑。一般曲轴悬臂、主轴承与副轴承处于曲柄销的一侧,曲轴的下端还紧固电机转子,如图1所示。曲轴所受的外载荷包括活塞、连杆、曲柄销及曲轴上平衡重的惯性力,活塞与气缸间及其他摩擦副的摩擦力,以及活塞所受的气体力。它们通过连杆大头与曲柄销传递给曲轴。对于冰箱压缩机,不仅惯性力是动态的,随转角变化,而且由于压比较大,活塞所受气体力在压缩机压缩或膨胀过程中会在很小的转角内急剧变化,因此冰箱压缩机滑动轴承负载变化剧烈,非线性强。另一方面,由于曲轴处于悬臂状态,因此压缩机工作时,曲轴在轴承孔中,转动与平移的同时,还会动态倾斜。这一方面恶化了主副滑动轴承的工作状态,另一方面也会引起压缩机整机的横向与倾斜振动。

由于滑动轴承对冰箱压缩机可靠性与性能的影响较大,国内外对其有不少研究[1-2]。但相对来说,针对连杆大头轴承的研究较多[1-3]。Kim研究了曲轴轴承的优化设计,求解了轴承油膜Reynolds方程与曲轴平衡方程,但没有考虑曲轴与电机转子的惯性力[4]。Kim和Han强调了模拟压缩机动态特性时,活塞与曲轴耦合分析的重要性,并且比较了计算曲轴润滑特性时采用不同轴承理论的差异[5]。Wisbeck使用有限容积法计算油膜力,不考虑转子与曲轴惯性力,但考虑接触力。计算轴承间隙时还考虑了曲轴与轴承磨损的影响[6]。Kurka在建立活塞压缩机动力学模型时,分析了黏弹性轴承负载[7]。郑铁生与Xie介绍了滑动轴承Reynolds方程的有限元解法及其在旋转压缩机曲轴-轴承系统动态分析中的应用[8-9]。Levecque在分析活塞压缩机振动时也考虑了曲轴的动态运动特性[10]。曲轴也是制冷活塞压缩机的易损件,Becerra对公交车空调压缩机曲轴的提前失效进行了分析[11]。另外,国内外对内燃机轴承的研究方法也可以作为本文研究工作的参考[12-13]。

目前大冷量、新制冷剂与变频是冰箱压缩机的发展方向。大冷量与采用新制冷剂R290会增加活塞气体力;变频压缩机高转速运行会增加惯性力,低转速时轴承油膜的承载能力会下降。这些都使得冰箱压缩机曲轴润滑与其动态特性问题更加突出。

本文采用汽缸内压力变化实测数据,考虑活塞、连杆与曲轴受力,建立了曲轴与电机转子横向位移与倾斜动力学方程;建立了有限长径向滑动轴承的油膜模型以求解轴承油膜力;计算分析了不同工况下,曲轴的动态特性与轴承轴芯和油膜厚度;观察测量了过负荷寿命试验后曲轴的磨损情况;分析了曲轴直径变化与转速增加时曲轴与轴承的工作状态。

1 数学模型

如图1所示,冰箱压缩机的曲轴与其电机转子紧固在一起,形成压缩机的转子。压缩机活塞将所受气体力、惯性力与摩擦力,以及连杆本身所受惯性力,通过连杆大头传递给曲轴曲柄销。冰箱压缩机的曲轴一般由滑动轴承悬臂支撑。压缩机稳定工作时,电机定子与转子横向电磁力很小,本文忽略不计。图1还表示了本文曲轴动力学分析的坐标系。坐标系z轴通过曲轴中心,指向气缸侧,原点o在整个转子的质心平面上,x轴沿气缸中心线由汽缸指向曲轴,x方向逆时针转过90°为y轴方向。另外,本文曲柄转向为逆时针,转角起始位置为活塞在上止点时。

1.1 曲轴载荷

曲轴所受外载荷Tc是由连杆大头对曲柄销的作用力(即连杆力)Fc以及曲柄销与曲轴平衡重的旋转惯性力组成。Tc在x轴与y轴的分量分别为

(1)

(2)

式中:Fp(θ)为活塞力,是气体力Fg(θ)、往复惯性力Fri(θ)和摩擦力Ff(θ)之和

Fp(θ)=Fg(θ)+Fri(θ)+Ff(θ)

(3)

(4)

(5)

(6)

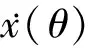
本文采用牛顿黏性定律估算活塞与汽缸摩擦力,而汽缸内气体压力随转角的变化pc(θ)根据试验数据插值计算得到。

1.2 滑动轴承有限元模型

曲轴上部靠近止推面滑动轴承为主轴承,靠近电机转子的为副轴承。由于曲轴悬臂,曲轴在轴承孔中转动时,其轴线与轴承孔不平行,油膜动态压力计算时要考虑曲轴的倾斜。考虑到冰箱压缩机主副滑动轴承的宽径比在0.5～2之间,本文采用有限长轴承理论,建立了径向滑动轴承的油膜有限元模型。考虑到此轴承直径为10～25 mm,转速为1 000～5 000 r/min,假设油膜流动为层流,忽略油膜质量力和惯性力,不计油膜的曲率,且压力、密度和黏度沿油膜厚度方向保持不变,从而有极坐标系下无量纲量Reynolds方程为

(7)

(8)

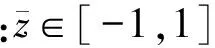
(9)

将求解域[0,2π]×[-1,1]剖分成(m×n)个矩形单元,单元刚度矩阵元素为

(10)

式中:η与ξ为单元坐标。油膜单元力向量元素为

(11)

由上述滑动轴承的有限元模型,给定轴承油膜厚度及其随时间导数,可以计算出主副轴承的油膜力在x轴与y轴上的分量Fox1、Foy1、Fox2、Foy2及力矩分量Mox1、Moy1、Mox2、Moy2。

1.3 曲轴动力学方程

若曲轴中心o点的位移为(xo,yo),曲轴在x方向和y方向的偏角分别为αx和αy,则得到曲轴在x方向和y方向的力平衡方程和矩平衡方程

(12)

式中:ms为曲轴和电机的质量和;Is为曲轴和电机沿x轴或y轴的转动惯量。

为了求解方便,本文将上述方程转变为曲轴两个平面上轴心位移的求解。若上轴承的轴颈上端面的位移用(x1,y1)表示,下轴承的轴颈下端面的位移用(x2,y2)表示,有

(13)

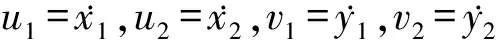
为了供油系统需要,冰箱压缩机曲轴直径一般选取较大,因此不会像滚动活塞压缩机曲轴那样有较大横向变形[9]。考虑到摩擦损失,目前其润滑油黏度也较低,轴承油膜局部压力不会引起较大的曲轴或轴承局部弹性变形。因此,本文不考虑曲轴与轴承的变形。这样由上述公式求出的曲轴两点位移及其导数,可计算出轴承油膜厚度及其随时间的变化。

2 计算结果与分析

2.1 压缩机主要设计参数与运行工况

表1是所研究的压缩机的主要设计参数。本文所采用的制冷剂为R600a,压缩机的运行工况如表2所示。

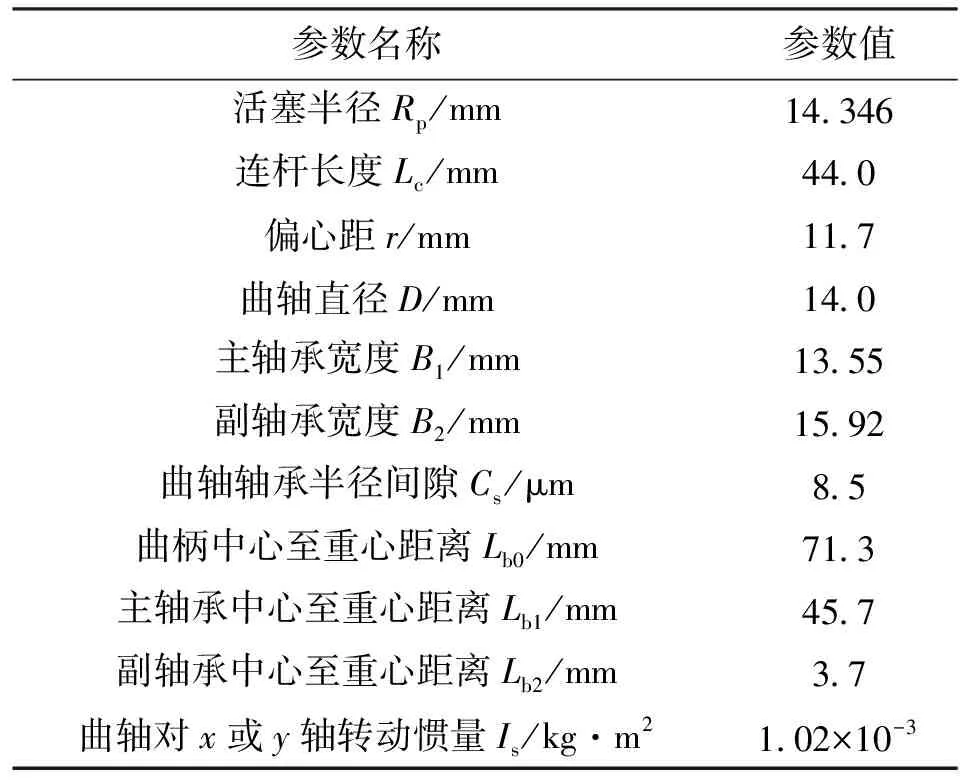
表1 压缩机主要设计参数

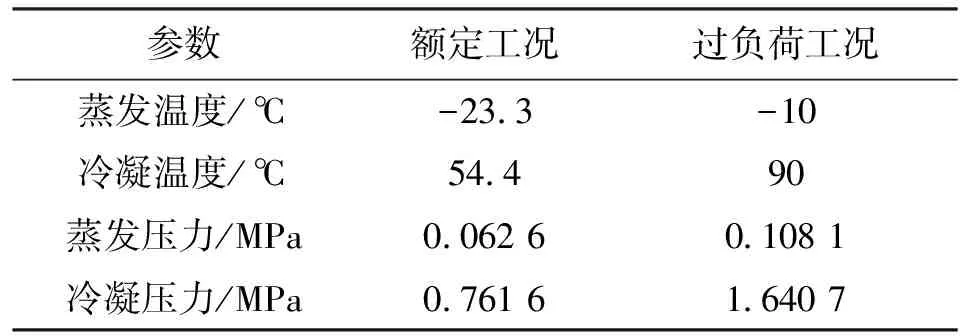
表2 压缩机运行工况

2.2 汽缸气体压力与曲轴载荷

图2是实测的压缩机在上述工况下汽缸内的气体压力变化情况。可以看出:两个工况下,压缩机余隙容积内制冷剂膨胀均需要曲轴转角约30°,而压缩过程中,气体压力均在曲轴转到300°时才大幅度升高。图3所示为额定工况和过负荷工况下的连杆力随曲轴转角的变化规律。两个工况下最大连杆力均发生在曲轴转角为330°附近,这与气缸内最大压力发生的角度基本相同,说明连杆力主要取决于气缸内的气体压力。图4是曲轴所受外载荷。可以看出,在曲轴转角在330°到360°范围内,曲轴所受外载荷的值较大;0°到330°转角内,其值较小,并且载荷与汽缸轴线的夹角变化较小。

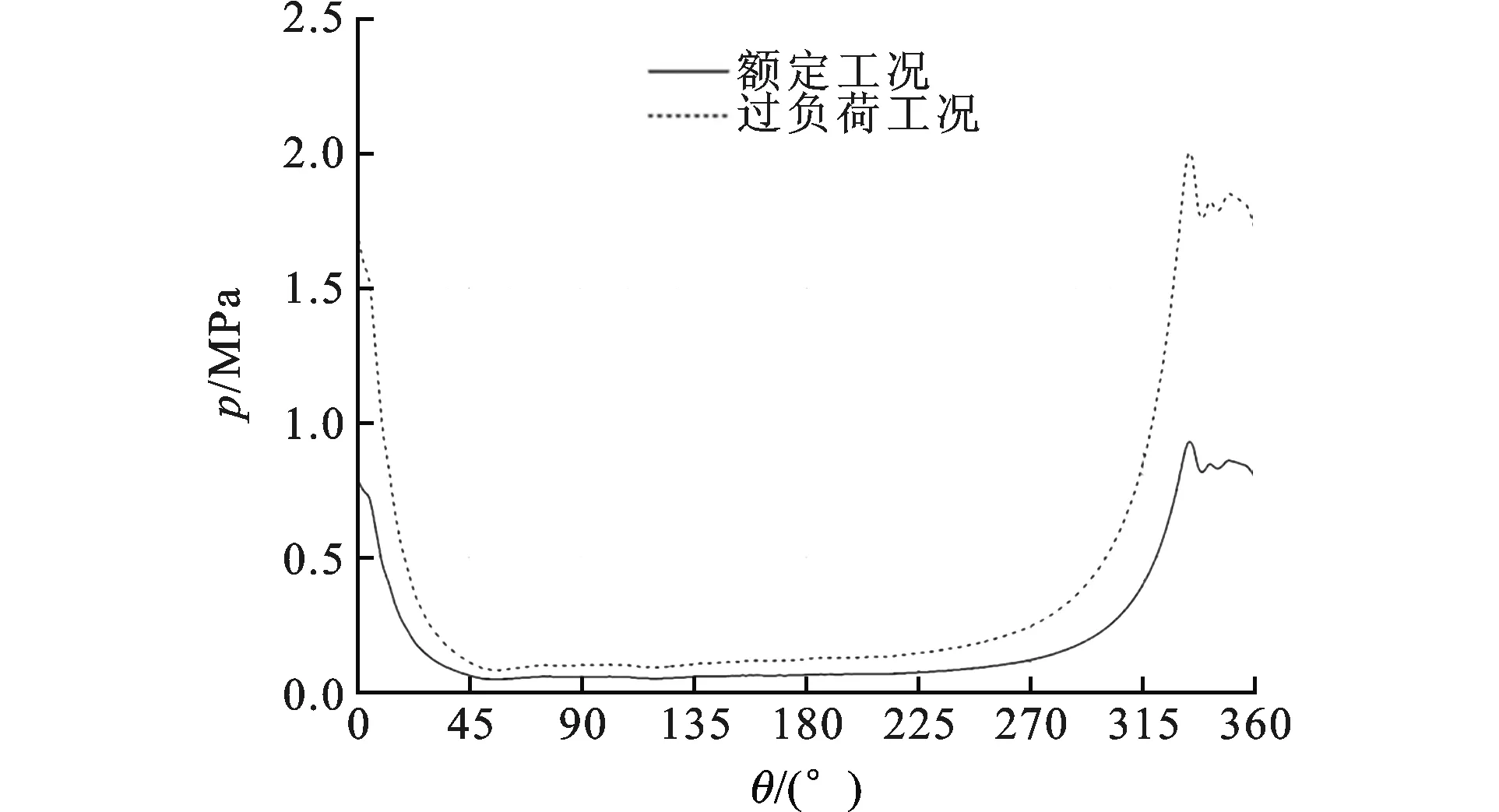
图2 实测的气缸内气体压力变化情况

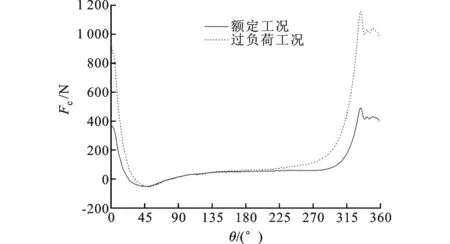
图3 两种工况下的连杆力

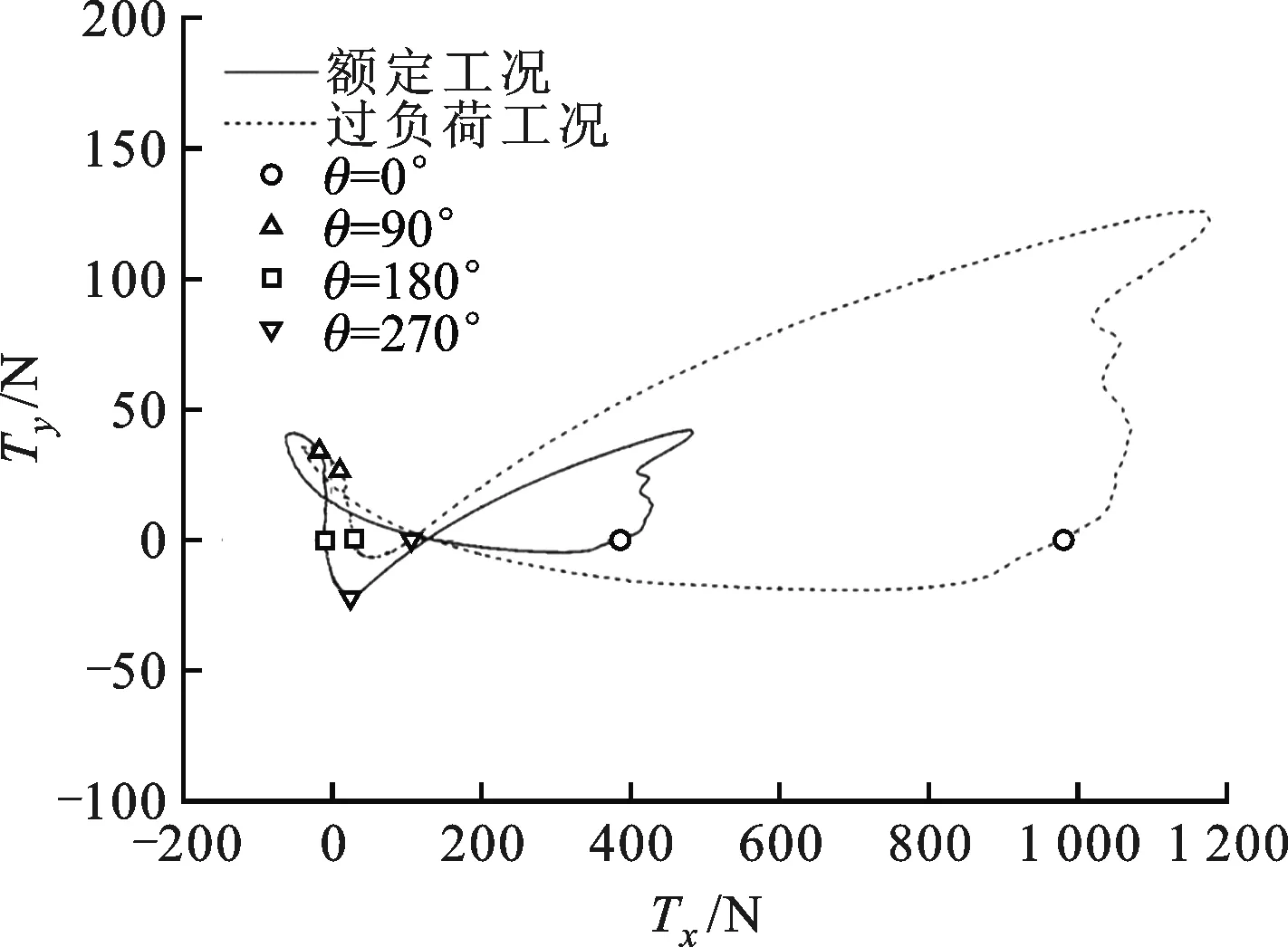
图4 两种工况下的曲轴载荷

2.3 额定工况与过负荷工况计算结果

图5为额定工况和过负荷工况下曲轴主副轴承不同截面处的轴心轨迹。从图5中可以看出,两个工况下,曲轴都明显倾斜。曲轴在轴承孔内,上部中心基本上在第一象限内,而下部在第三象限。转角为0°时,曲轴倾斜最大,倾斜方向基本在x轴平面内;转角为90°时,曲轴基本与轴承孔平行;转角为180°时,曲轴在y轴平面内倾斜;转角300°以后,气体力极速增大,主轴承偏心率也急剧增大。虽然过负荷工况下,曲轴外载荷比额定工况下大很多,但主轴承偏心率变化不大,只是大偏心率的转角范围较大,副轴承偏心率明显加大,油膜变薄。

①:轴承上端;②:轴承中部;③:轴承下端(a)额定工况

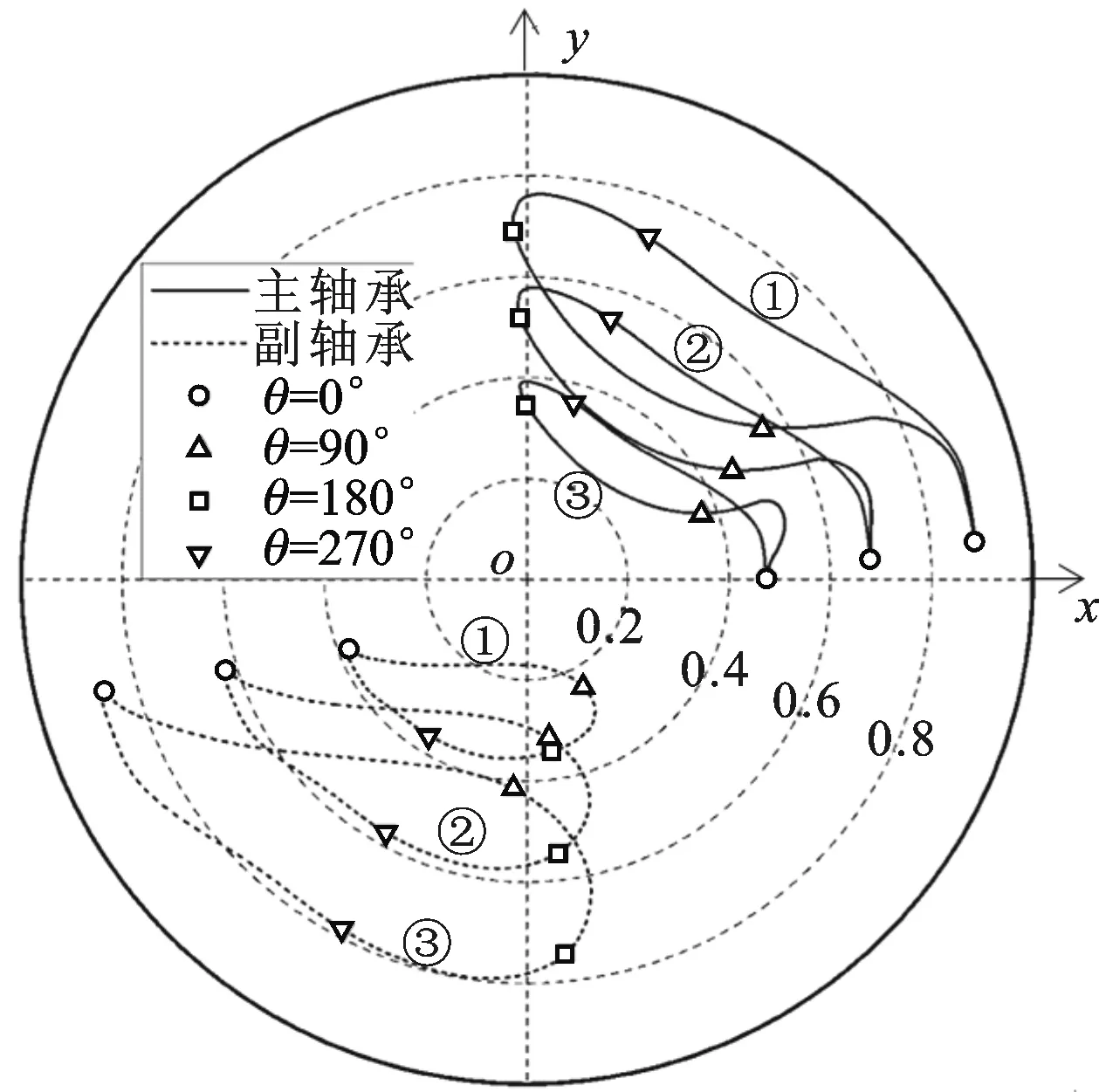
①:轴承上端;②:轴承中部;③:轴承下端(b)过负荷工况图5 不同工况下曲轴轴心轨迹

曲轴上部轴心相对偏移量都接近0.9,油膜厚度约1 μm。考虑到曲轴与轴承的加工精度,曲轴上部平衡重一侧与轴承孔上部汽缸对面一侧会发生偏磨。这时曲轴副轴承下端偏心率最大,两个工况下分别为0.74与0.84,油膜厚度分别为2.2 μm与1.1 μm时,也会发生偏磨。

2.4 试 验

图6为研究样机在过负荷工况下1 000小时试验后曲轴的磨损情况。可以看出,曲轴磨损集中在上端与下端,且上端磨损比下端严重。本文还分别测量了曲柄、曲轴主轴承和副轴承上端、中部和下端的圆度。曲轴对应主轴承部分测量圆度分别为3.66、3.72和1.70 μm;对应副轴承部分测量圆度分别为2.67、3.16和3.50 μm。这与上述对于曲轴轴承的润滑分析结果相符。

图6 过负荷寿命试验后曲轴磨损情况

2.5 曲轴直径对轴承的影响

本文还研究了曲轴直径对轴承的影响。图7a、7b分别为额定工况下曲轴直径减少或增加时2 mm时的轴心轨迹。表3为不同曲轴直径时轴承最大偏心率和最小油膜厚度。可以看出,曲轴直径增加时,主副轴承最大偏心率减少,最小油膜厚度明显增加。

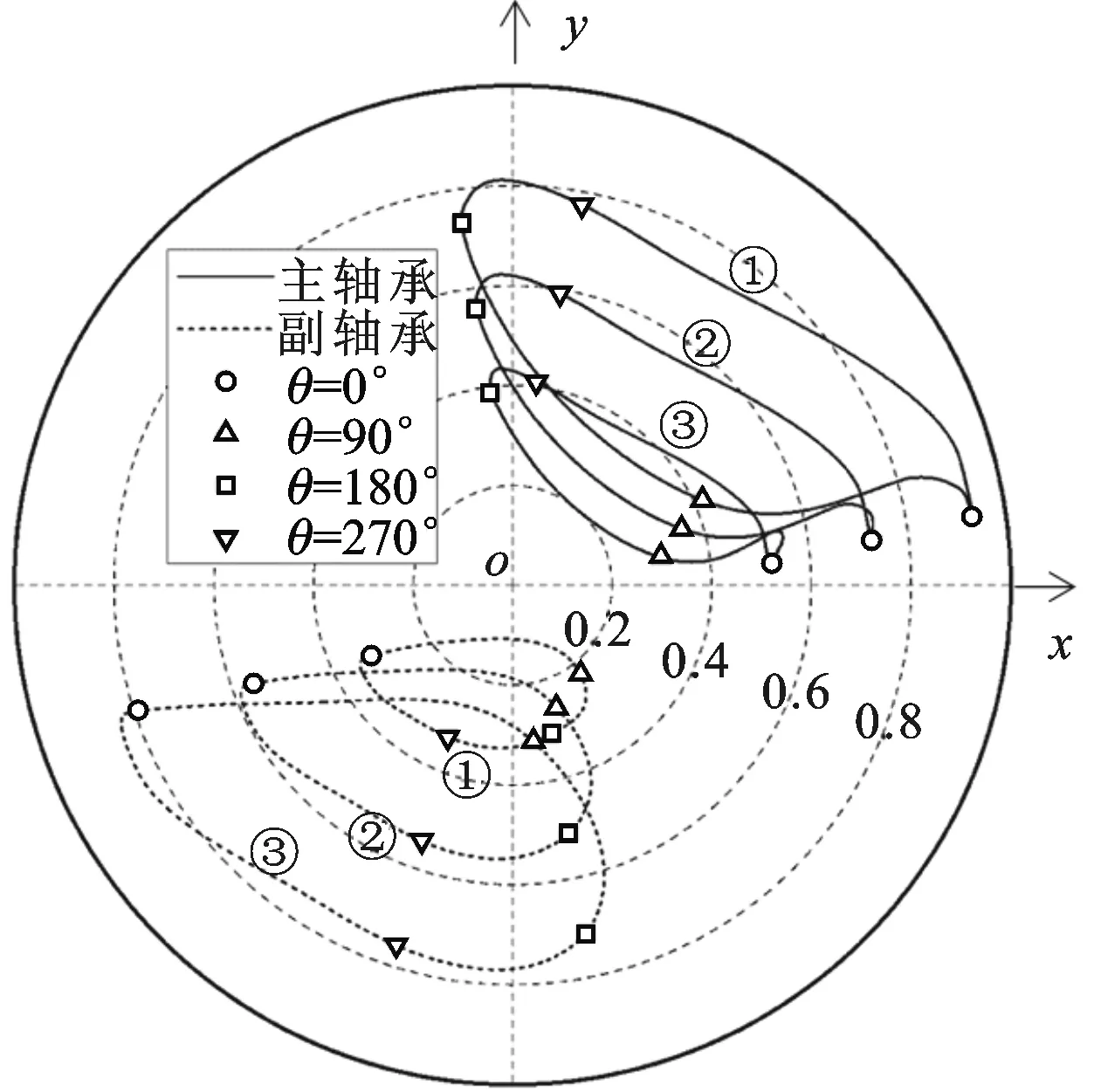
①:轴承上端;②:轴承中部;③:轴承下端(a)ds=12 mm

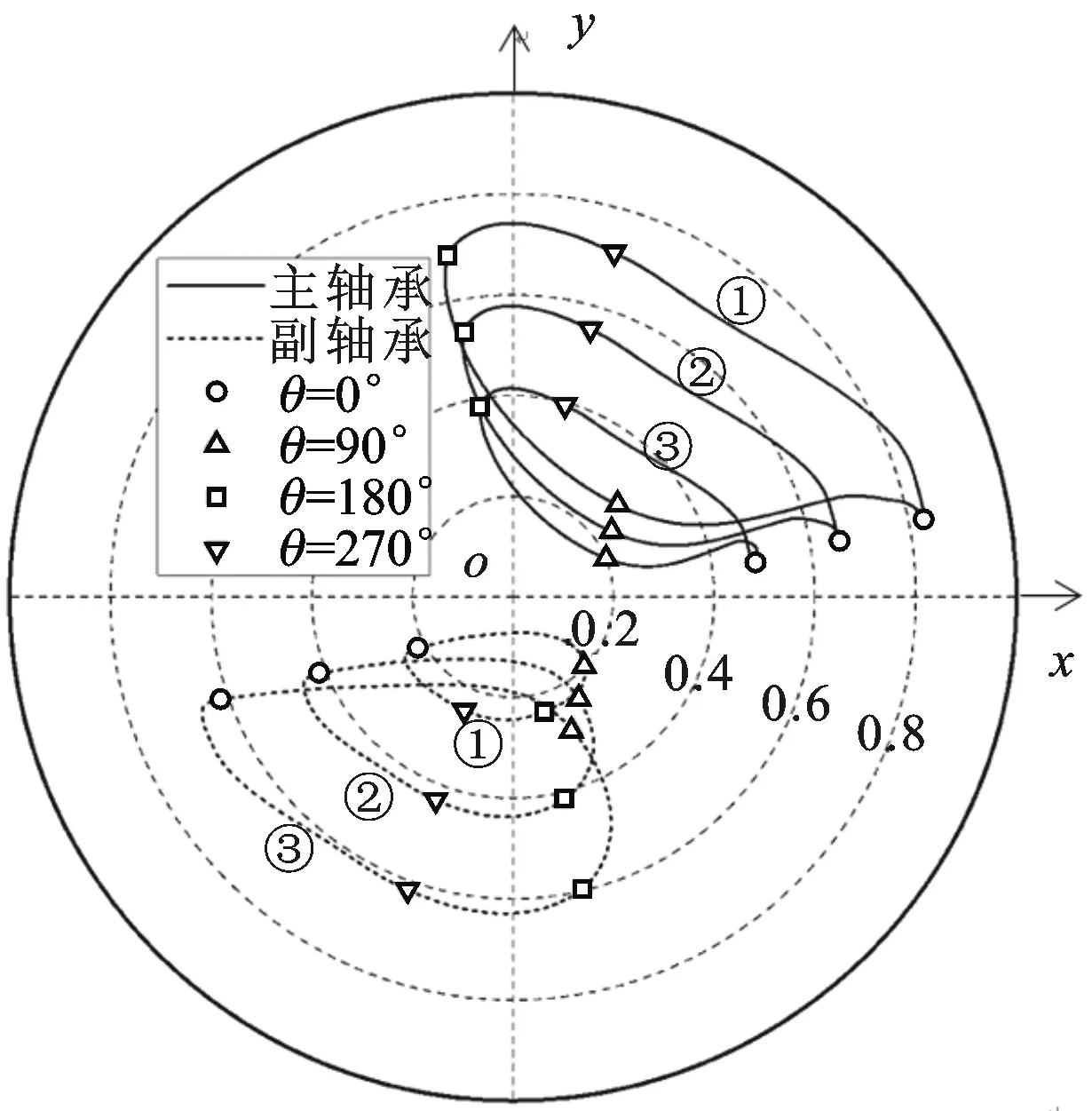
①:轴承上端;②:轴承中部;③:轴承下端(b)ds=16 mm图7 不同曲轴直径时曲轴轴心轨迹

表3 不同曲轴直径时轴承最大偏心率和最小油膜厚度

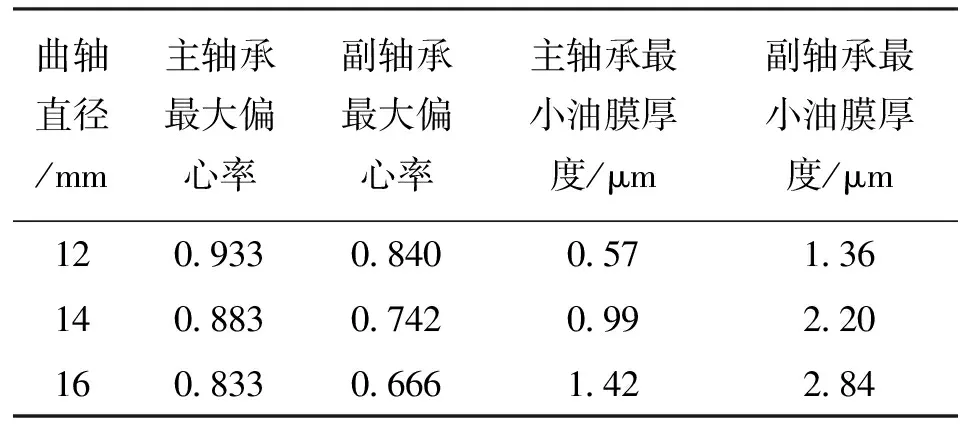
曲轴直径/mm主轴承最大偏心率副轴承最大偏心率主轴承最小油膜厚度/μm副轴承最小油膜厚度/μm120933084005713614088307420992201608330666142284

2.6 转速对轴承的影响

图8为额定工况下不同转速时曲轴主副轴承的轴心轨迹。可以看出:转速增大时,主轴承最大偏心距增大,最小油膜厚度减小;副轴承的最大偏心距减小,最小由膜厚度增加。因此,对于研究样机,转速的增大会使主轴承磨损恶化,而副轴承磨损有所改善。

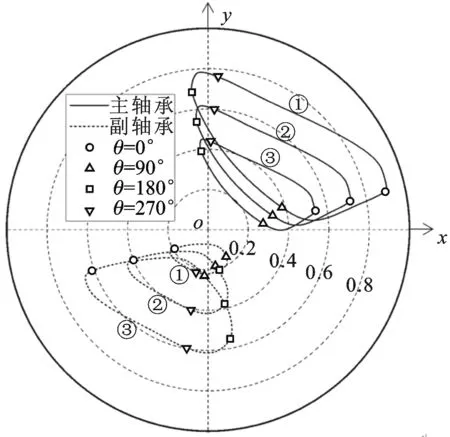
①:轴承上端;②:轴承中部;③:轴承下端图8 转速为3 940 r/min时曲轴轴心轨迹

3 结 论

本文探索了往复式冰箱压缩机受动态气体力与惯性力作用的悬臂曲轴动态特性和其主副滑动轴承油膜厚度的计算方法。以R600a往复式冰箱压缩机曲轴及其轴承为研究对象,分析了其外载荷,研究了曲轴轴承的流体动力润滑,建立了曲轴轴心轨迹的计算模型,编制了程序进行数值模拟,并观测与测量了过负荷工况下寿命试验后曲轴磨损情况,验证了数值模拟的合理性。可得出以下结论。

(1)压缩机工作时,曲轴除转动与平移外,倾斜方位与角度也在不断变化,但上部中心基本上在第一象限内,而下部在第三象限。转角为0°时,曲轴倾斜最大。

(2)在两个工况下,曲轴上部偏心率为0.9,油膜厚度为1 μm。曲轴与轴承孔上部会发生偏磨。轴承与轴承孔下端过负载工况油膜厚度较小,也会发生偏磨。这与样机过负荷1 000 h试验后曲轴磨损观测及圆度检测情况一致。

(3)增加曲轴直径,主副轴承最大偏心率都会减少,最小油膜厚度明显增加。

(4)转速增大会使主轴承油膜减少,而副轴承油膜厚度增加。

[1] HURST C J, KELLY A D. Non-destructive assessment of wrist journal bearings in hermetic reciprocating compressors [C]∥Proceedings of the International Compressor Engineering Conference. Purdue, IN, USA: Purdue University, 1998: 31-36.

[2] TASSOU S A, GRACE I N. Fault diagnosis and refrigerant leak detection in vapour compression refrigeration systems [J]. International Journal of Refrigeration, 2005, 28(5): 680-688.

[3] LEE K H, KIM J W, HUA Y J, et al. Optimum design of dynamically-loaded journal bearing with R600a refrigerant application [C]∥Proceedings of the International Compressor Engineering Conference. Purdue, IN, USA: Purdue University, 1998: 153-158.

[4] KIM B J, PARK J S, KIM D H, et al. Design of journal bearings in reciprocating compressors [EB/OL]. [2014-07-20]. http:∥docs.lib.purdue.edu.cn/icec/1535.

[5] KIM T J, HAN J S. Comparison of the dynamic behavior and lubrication characteristics of a reciprocating compressor crankshaft in both finite and short bearing models [J]. Tribology Transactions, 2004, 47(1): 61-69.

[6] WISBECK H J, MANKE A L, PRATA A T. Bearing system in dynamic loading including solid contact and wear [EB/OL]. [2014-07-20]. http:∥docs.lib. purdue.edu.cn/icec/1532.

[7] KURKA P R G, IZUKA J H, PAULINO K L G. Dynamic loads of reciprocating compressors with flexible bearings [J]. Mechanism and Machine Theory, 2012, 52: 130-143.

[8] 郑铁生, 李立, 许庆余. 一类椭圆型变分不等式离散问题的迭代算法 [J]. 应用数学和力学, 1995, 16(4): 329-335. ZHENG Tiesheng, LI Li, XU Qingyu. Iterative algorithm of a kind of elliptic variational inequality discrete problem [J]. Applied Mathematics and Mechanics, 1995, 16(4): 329-335.

[9] XIE F, ZHANG H F, WU J H, et al. Dynamic analysis of a rotor-journal bearing system for rotary compressor [EB/OL]. [2014-07-20]. http:∥docs.lib. purdue.edu.cn/icec/1820.

[10]LEVECQUE N, MAHFOUD J, VIOLETTE D, et al. Vibration reduction of a single cylinder reciprocating compressor based on multi-stage balancing [J]. Mechanism and Machine Theory, 2011, 46(1): 1-9.

[11]BECERRA J A, JIMENEZ F J, TORRES M, et al. Failure analysis of reciprocating compressor crankshafts [J]. Engineering Failure Analysis, 2011, 18(2): 735-746.

[12]孙军, 蔡晓霞, 刘利平, 等. 计入机体和曲轴变形的曲轴轴承弹流润滑分析 [J]. 内燃机学报, 2010, 28(3): 275-280. SUN Jun, CAI Xiaoxia, LIU Liping, et al. Analysis of elastohydrodynamic lubrication of crankshaft bearing considering deformation of engine block and crankshaft [J]. Transactions of CSICE, 2010, 28(3): 275-280.

[13]贾德文, 申立中, 毕玉华, 等. 柴油机连杆大头轴承润滑特性影响因素的研究 [J]. 汽车工程, 2012, 34(11): 981-984. JIA Dewen, SHEN Lizhong, BI Yuhua, et al. A study on the factors affecting the lubrication characteristics of connecting rod big-end bearing in diesel engine [J]. Automotive Engineering, 2012, 34(11): 981-984.

(编辑 刘杨 苗凌)

Numerical Analysis for the Crankshaft’s Dynamic Behavior and Bearing Lubrication of Reciprocating Refrigerator Compressor

WU Jianhua1,LEI Yuan1,WANG Gang1,YANG Hua2,LU Longquan2

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. Jiaxipera Compressor Co. Ltd., Jiaxing, Zhejiang 314006, China)

A method to analyze dynamic behavior of cantilever crankshaft and to calculate the oil film thickness of main and sub bearings under dynamic loading of reciprocating refrigerator compressor is proposed. Transversal and tilt displacement dynamic equations for the crankshaft and the motor rotor are built by considering the gas force and inertia force of piston, connecting rod and crankshaft and using the measured data of pressure within the cylinder A finite element (FE) model for the oil film of the finite journal bearing is established by adopting the FE discrete method for numerical approximation. Crankshaft wear is observed and its roundness is measured after the life test under an over load operating condition. The analysis results show that the angle of inclination of crankshaft constantly changes during the operation of compressor, while the upper center is basically in the first quadrant, and the lower is in the third quadrant. The largest crankshaft incline reaches when its rotational angle is 0°. The eccentric wear between crankshaft and the upper bearing hole happens under the rated load and overload conditions, while the eccentric wear between bearing and the lower bearing happens under the overload condition. The oil film thickness of sub bearing increases and the oil film thickness of main bearing decreases when the rotation speed increases.

reciprocating refrigerator compressor; crankshaft; bearing; lubrication

2014-08-04。

吴建华(1963—),男,副教授。

国家科技支撑计划资助项目(2012BAF01 B05)。

时间:2014-11-28

10.7652/xjtuxb201502010

TB652

A

0253-987X(2015)02-0055-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141128.1611.001.html