采用紧束缚格林函数法研究原子吸附石墨烯纳米带电子输运
李昕,张永,殷德民,王小力,刘卫华
(西安交通大学电子与信息工程学院,710049,西安)
采用紧束缚格林函数法研究原子吸附石墨烯纳米带电子输运
李昕,张永,殷德民,王小力,刘卫华
(西安交通大学电子与信息工程学院,710049,西安)
采用紧束缚非平衡格林函数法分析了扶手椅型石墨烯纳米带(AGNR)和锯齿形石墨烯纳米带(ZGNR)器件吸附H、F、O和OH这4种原子的电子输运特性。用π电子结构体系的紧束缚理论分析了GNR的电子结构;用紧束缚扩展休克理论计算了GNR碳原子与所吸附原子间的电子相互作用;用非平衡格林函数法仿真了GNR吸附原子后的电流特性。研究结果表明:在平衡态下,AGNR吸附H原子后对器件的输运谱影响最大,而吸附OH原子后使GNR的禁带宽度增加0.3 eV;在非平衡态下,吸附H原子不仅增加了导带底附近态密度,而且直接在禁带引入了杂质能级,从而提高了AGNR器件产生的电流;H原子吸附在ZGNR器件产生的电流约是吸附在AGNR电流的1.5倍;H原子吸附在GNR非边界处比吸附在边界处产生的电流高。该研究结果可以对提高石墨烯气敏传感器和生物传感器的灵敏度提供理论基础。
石墨烯纳米带;原子吸附;紧束缚;格林函数;输运谱
对无机分子和高分子等的高灵敏度、高分辨率检测在生物和化学领域一直受到关注。在医学领域的理想分辨率甚至达到单个分子或原子的级别[1-4]。石墨烯的发现和其优越的电学特性开启了对这个材料越来越多的研究热潮。因为石墨烯的晶格完整,载流子迁移率高,可以感知单个分子和原子的吸附引起的能带结构和电子输运变化,进而影响器件的输出特性。这种微弱电流特性变化的检测可以识别吸附气体或原子的属性[5],这使得石墨烯纳米带(graphene nano ribbon, GNR)器件在传感器领域有了很好的应用前景。
关于GNR的气体吸附特性已经有了较多的研究报道[6-8]。以密度泛函理论为核心的第一性原理被用来计算不同原子吸附在GNR上的电子结构,分析吸附原子与GNR之间的电荷转移,判断原子的最稳定吸附位置和原子吸附对GNR几何结构的影响[9]。这种方法能精确地处理GNR的电子分布问题,但是计算时间较长。GNR的能带也可以通过最近邻紧束缚法快速求得[10],但该方法仅考虑了被吸附原子与GNR之间的π电子作用。将紧束缚理论和密度泛函理论二者相结合的扩展休克理论能较好地处理所有价电子的相互作用关系[10]。关于GNR器件特性分析,目前主要采用基于非平衡格林函数法的量子输运模型,该模型可以分析关于不同边界结构的GNR器件的电子输运特性[11-12],以及分析GNR吸附不同原子引起的电子分布、电子输运变化等。
本文在GNR平面通过吸附原子构造新的沟道结构,并尝试从器件的角度来探索其输运特性。用紧束缚理论分析原子吸附下GNR的电子结构,用扩展休克理论分析吸附原子与GNR的相互作用,以及不同吸附原子对GNR器件的输运谱、态密度和电流的影响。在输运求解过程中,通过引入自能矩阵将包含吸附原子的GNR体系的哈密顿矩阵转化成吸附原子对GNR哈密顿矩阵的修正,用求解二维结构电子输运方法来实现复杂的准三维结构电子输运问题的求解。
1 含有原子吸附的GNR器件求解
GNR器件的电子输运求解主要包括器件电子结构分析,器件静电特性分析和量子输运分析3个过程。含原子吸附的GNR电子结构主要包括GNR自身的电子结构、吸附原子的电子结构和GNR与吸附原子之间的电荷转移。用紧束缚理论描述含吸附原子的GNR体系[13]方程如下
H=HGNR+Ha+Hint-GNR
(1)
式中:HGNR是GNR的哈密顿矩阵;Ha是吸附原子自身的哈密顿矩阵;Hint-GNR是GNR和吸附原子的作用矩阵。在量子输运中,纳米器件的电极对沟道注入电子的过程可以用自能矩阵来描述,吸附原子与GNR之间的电荷转移过程也可以理解成吸附原子对GNR的电子注入或吸收。所以,含吸附原子的GNR体系的哈密顿矩阵可以认为是GNR吸附原子前的哈密顿矩阵加上吸附原子对被吸附碳原子的位能矩阵和被吸附碳原子与其最近邻3个碳原子相互作用的矩阵。这样,含有吸附原子的GNR体系的哈密顿量可以写成二维矩阵形式
(2)
式中:HGNR-a是GNR对吸附原子的作用矩阵;Ha-GNR是吸附原子对GNR的作用矩阵。
用格林函数法处理二维哈密顿矩阵,可以得到GNR体系的格林函数为
[EI-HGNR-HGNR-a(EI-Ha)-1Ha-GNR]GGNR=I
(3)
式中:E是能量;I是单位矩阵;GGNR是GNR哈密顿矩阵的格林函数。
GNR在受到吸附原子影响下的有效哈密顿矩阵为
Heff=HGNR+HGNR-a(EI-Ha)-1+Ha-GNR
(4)
用非平衡格林函数求解GNR器件的输运过程,要考虑电极电压对格林函数的影响。沟道的非平衡格林函数为[14]
(5)
式中:ΣS和ΣD分别是源和漏的自能矩阵,它反映半无限电极对沟道哈密顿矩阵的非共轭部分,其表达式为
(6)
式中:τS,D为沟道与源漏电极的耦合矩阵;G是电极的表面格林函数,它只考虑电极中与沟道相连原子的作用,而GGNR考虑了所有电极原子;U为沟道的电压分布,可以通过求解泊松方程来得到。根据二维泊松方程在沟道中的碳原子构成的GNR正六边形网格上的差分格式可以得到沟道电压为[14]
(7)
式中:a是GNR晶格常数;ε0和εr分别是真空介电常数和GNR的相对介电常数;n是碳原子处的电荷密度;Ub为电势的边界条件;D为二阶导的矩阵算符。最后通过广义Landauer Formalism的公式可以得到在非平衡条件下沟道电流方程
(8)
式中:h为普朗克常量;e为电子电荷;f1(E)、f2(E)分别为左、右电极的费米分布。
2 结果和讨论

图1 含原子吸附的AGNR两端器件示意图

图2 4种原子与AGNR表面碳原子成键结构示意图
在这里主要讨论的是含原子吸附的扶手椅型GNR(armchair GNR, AGNR)两端器件的电流特性。图1为器件结构示意图,两端的源电极和漏电极都采用与沟道相同边界结构的AGNR,单个原子吸附在沟道中AGNR上的A点位置,即近邻边界的碳原子上。以下研究H、F、OH和O这4种原子的吸附对AGNR两端器件电流特性的影响。4种原子被吸附后会与AGNR表面的碳原子成键而构成最稳定的吸附位置,H、F、OH、O距离石墨烯中碳原子的距离分别是0.035、0.036、0.041和0.147 nm,如图2所示。不同原子的吸附对GNR紧束缚参数的影响见表1[13]。表1中Ea是吸附原子对碳原子的位能影响参数,它是从GNR的狄拉克点计算得到的,γa-C,2pz反映了被吸附原子的电子与吸附碳原子的2pz轨道电子之间的相互作用能,γC,2pz-2pz是吸附碳原子的2pz轨道电子在被吸附原子的微扰下与最近邻碳原子的2pz轨道电子相互作用能的修正值。Ea、γa-C,2pz和γC,2pz-2pz都是与碳原子π轨道电子相互作用能的比值,所有电子轨道的作用不包括碳原子的2s、2px和2py原子价电子轨道。假设吸附原子只对被吸附的碳原子有作用,而不影响GNR的结构,可以得到这些吸附模型的哈密顿矩阵为
H=Hπ+Heff=Hπ+ΣγC,2pz-2pz+
γa-C,2pz(EI-εa)-1γa-C,2pz
(9)
式中:Hπ是沟道石墨烯带碳原子π轨道电子的哈密顿矩阵,Heff是吸附原子对沟道石墨烯带哈密顿矩阵的影响;E是能量。

表1 GNR吸附不同原子后的紧束缚参数
2.1 不同原子的吸附对AGNR器件输运谱和态密度的影响
假设原子吸附在AGNR器件沟道中,H、F、O和OH这4种原子都吸附在相同的位置上,即图1中的A位置。根据前面的理论分析进行求解,得到器件在平衡态的传输系数和非平衡态的态密度(DOS)特性如图3和图4所示。
通常的,只有费米能级附近电子的输运才能产生电流,所以重点讨论吸附原子在费米能级附近引起的态密度和传输系数的变化。在平衡态下,费米能级取在能量为零的位置。对比分析图3a的5种情况可知,H的吸附对器件传输系数的影响最大,在电子能量为1.5~4.5 eV范围内,对比没有吸附原子的情况,所有吸附原子都使传输系数下降,其中吸附H后从2.0下降到1.0附近,下降范围最大。在电子能量为1.0~1.5 eV范围内,其他吸附原子的下降幅度较小,H原子引起传输系数的下降最大特别是在1.0 eV附近(见图3b)。值得注意的是,GNR在吸附OH原子后,在1.0~1.5 eV范围内器件的传输系数几乎为0,使禁带宽度增加了0.3 eV,这说明OH原子吸附有增加禁带宽度的趋势。

(a)电子能量范围为-5~5 eV时的传输系数
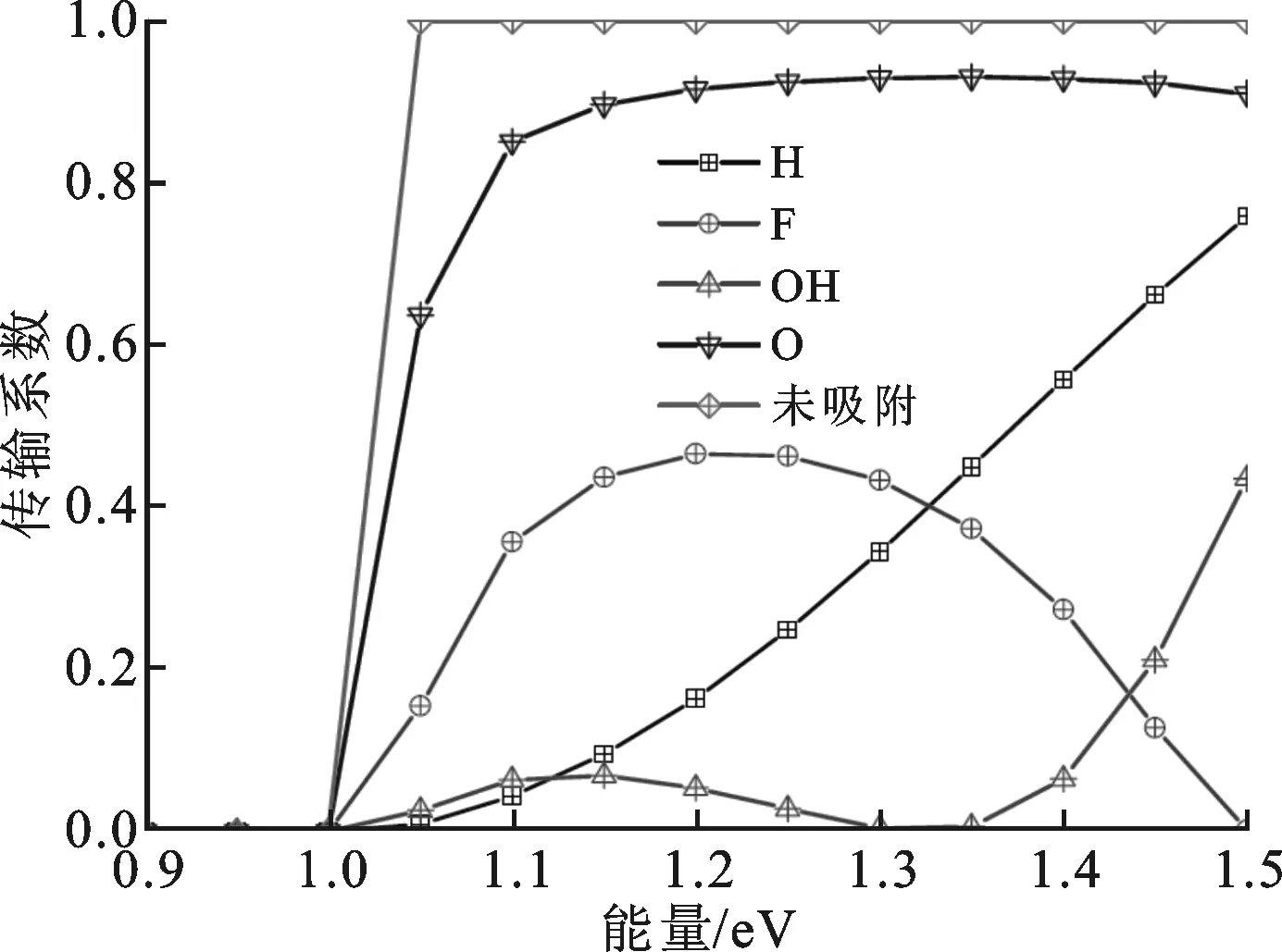
(b)电子能量范围为0.9~1.5 eV时的传输系数 图3 平衡态(0 V偏压)下吸附与未吸附4种原子时AGNR器件的输运谱
在非平衡态下(两端施加1 V电压),价带顶附近(电子能量在-4~0.5 eV之间)不同原子的吸附对态密度影响不大。不过在导带底附近(电子能量在0~4 eV之间)吸附原子对态密度影响较大,从左至右依次出现几个尖峰,对应的分别为吸附H、OH、F和O原子(见图4b),这说明吸附H原子对靠近导带底附近态密度增加贡献最大,有利于电流的传输。图4b中也发现O原子在非占据态的态密度的峰值最大,但是它离费米能级较远,所以对电子的输运贡献较小,同样,图4a中虽然没有吸附原子的AGNR在占据态的态密度峰值也很大,但是它离费米能级较远,所以对电子的输运贡献也较小。

(a)电子能量为-8~8 eV范围时的态密度

(b)电子能量为0~4 eV范围时的态密度 图4 非平衡态(1 V偏压)下吸附与未吸附4种原子时AGNR器件的态密度分布特性曲线
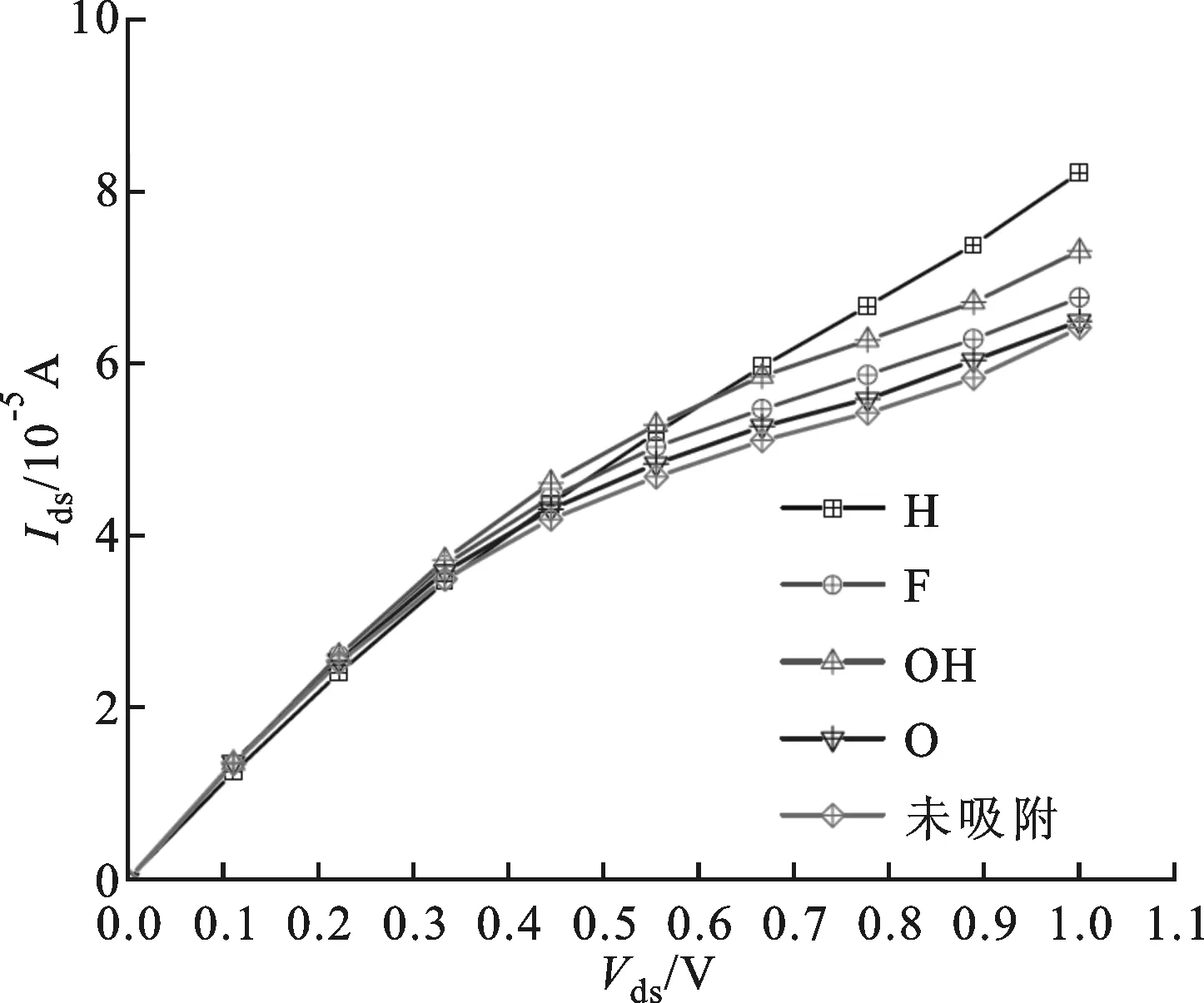
图5 AGNR器件吸附与未吸附4种原子后的电流特性曲线
2.2 不同原子吸附对AGNR器件电流的影响
分别吸附H、F、O和OH 4种原子后AGNR器件的电流特性如图5所示。从图中可以看出,器件吸附原子后电流都增加了,但是增加的幅度不同,这主要是因为不同原子与AGNR碳原子成键后的电荷转移特性不同所导致。要从吸附原子的核外电子轨道分布和与碳原子的成键方式来分析吸附原子对AGNR器件电流的影响。
由图5可以明显看到,吸附H原子产生的电流最大,这是因为H原子的1s轨道对器件的电导影响最大,且与C原子的距离最近(参见图2),与C原子的2pz轨道交叠的比较多。其后依次为OH、F和O原子。F原子有2个共价轨道,分别为2s和2pz,在紧束缚模型中,这2个轨道代表2个独立的电子输运沟道,其输运特性正比于γa-C,2pz的大小,所以从表1中可见,2s比2pz对电导的贡献更大。OH与AGNR的吸附原理主要是O原子在C原子正上方与C共价成键,O和F原子一样通过2s和2pz轨道影响电子的电导。由于O的电导特性和F原子的比较类似,因此吸附了F和OH之后器件的电流均小于吸附H的电流。只有O原子是二价的,它与2个相邻的C原子进行成键,不像其他3种原子只与AGNR的一个碳原子成键或者吸附,而是与AGNR的2个不同晶胞原子进行杂化,抑制了电子在石墨烯带中的传导,所以吸附O原子产生的电流最小。
在吸附原子和被吸附碳原子及其相邻碳原子处容易形成电子局域化现象是GNR器件的特点,特别在狄拉克点附近更是如此,以下通过AGNR器件吸附H、F、OH和O原子后的局域态密度变化来分析电流特性。图6所示分别为H、F、OH和O吸附在AGNR后的局域态密度和总体态密度分布对比图。AGNR器件吸附H原子后在禁带引入了杂质能级,所以减小了原来AGNR器件的禁带宽度。在图6a中引入的杂质能级与导带相邻,不是深局域能级,该能级的电子较容易跳跃到导带参与电子传输,所以有利于提高器件的电流。AGNR器件吸附F、OH和O原子后并没有像吸附H原子那样直接在禁带引入了杂质能级(见图6b~6d),而是在占据态和非占据态分别引入能级进行杂化,所以这些引入能级是非局域态的。由图6c可见,OH原子引入能级最接近导带底,紧接着分别是F原子和O原子引入的能级。这与图5的电流增加趋势相吻合。虽然,这3种吸附原子使占据态和非占据态的态密度都得到相应的提高,但是由于真正参与输运的电子多分布在导带底或价带顶处,所以这些非局域态能级对提高GNR器件电流的贡献不如H原子大。
2.3 石墨烯吸附H原子在不同位置对器件电流的影响

(a)H原子吸附

(b)F原子吸附

(c)OH原子吸附

(d)O原子吸附 图6 4种原子吸附在GNR上的局域态密度和总体态密度分布图

图7 AGNR和ZGNR不同位置上吸附H原子示意图
由于GNR器件的电子在整个沟道区进行传输,在边界处的吸附位置的不同对输运谱有很大影响,所以分别针对扶手椅型(AGNR)和锯齿形(zigzag GNR,ZGNR)2种边界的石墨烯带中比较有代表的位置,即边界和近邻边界的碳原子上,研究H原子吸附位置和器件电流的相关关系。图7是AGNR和ZGNR不同位置上吸附H原子示意图。其中位置1代表吸附物在AGNR的边界碳原子上,2代表吸附物在AGNR的非边界碳原子上,3代表吸附物在ZGNR的边界碳原子上,4代表吸附物在ZGNR的非边界碳原子上。2种类型的GNR的长和宽尺度都在1 nm左右,其中AGNR的长为0.71 nm,宽为0.74 nm,ZGNR的长为0.61 nm,宽为0.71 nm。得到的4种电流特性如图8所示,可以看到H原子吸附在ZGNR非边界时得到的电流最大,而且无论吸附在边界还是非边界,ZGNR器件产生的电流大约是AGNR器件产生电流的1.5倍。H原子吸附在非边界时的电流比在边界时的电流要高,这与器件的边界状态有关,这也表明电子在GNR的输运是沿着一定路径的。相比较而言,ZGNR更有前途成为气敏传感器的敏感材料。

图8 不同位置上吸附H原子的GNR器件电流特性
3 总结与展望
本文基于紧束缚格林函数法分析了AGNR和ZGNR两端器件吸附H、F、OH和O的输运特性。主要探讨不同原子吸附对器件输运谱、态密度和电流的影响,也初步分析原子吸附位置和器件边界结构对电流的影响。平衡态下,吸附H原子后对AGNR器件的输运谱影响最大,而吸附OH原子有增加禁带宽度的趋势。非平衡态下,吸附H原子一方面增加了导带底附近态密度,这是因为H原子的1s轨道对器件的电导影响最大,且与C原子的距离最近,与C原子的2pz轨道交叠得比较多。其后依次为OH、F和O原子。另一方面,H原子的吸附直接在禁带引入了杂质能级,对AGNR器件产生的电流最大,而F、OH和O原子的吸附只是在占据态和非占据态分别引入非局域态能级进行杂化,对电流的贡献较小。将单个H原子分别吸附在AGNR和ZGNR的边界和非边界的碳原子上,发现后者得到的电流更大。而无论边界还是非边界,H原子吸附在ZGNR得到的电流是吸附在AGNR电流的1.5倍。对GNR器件吸附特性的分析不仅有助于GNR传感器的研究,而且采用不同的原子吸附也可以构造新的器件结构。
[1] PEREIRA V M, DOSSANTOS J M B L, NETO A C. Modeling disorder in graphene [J]. Physical Review: B, 2008, 77(11): 115109.
[2] FASOLINO A, LOSJ, KATSNELSON M I. Intrinsic ripples in graphene [J]. Nature Materials, 2007, 6(11): 858-861.
[3] NAKADA K, FUJITA M, DRESSELHAUS G, et al. Edge state in graphene ribbons: nanometer size effect and edge shape dependence [J]. Physical Review: B, 1996, 54(24): 17954-17961.
[4] 李昕, 郭士西, 宋辉, 等. 石墨烯晶体管研究进展 [J]. 西安交通大学学报, 2014, 48(10): 1-8. LI Xin, GUO Shixi, SONG Hui, et al. Latest advance of researches on graphene transistors [J]. Journal of Xi’an Jiaotong University, 2014, 48(10): 1-8.
[5] 李昕, 张娟, 李全福, 等. 面向集成电路的大尺寸单晶石墨烯的可控制备方法 [J]. 西安交通大学学报, 2014, 48(6): 103-109. LI Xin, ZHANG Juan, LI Quanfu, et al. A controllable preparation method for IC oriented large scale single crystal graphene [J]. Journal of Xi’an Jiaotong University, 2014, 48(6): 103-109.
[6] HUANG B, LI Z, LIU Z, et al. Adsorption of gas molecules on graphene nanoribbons and its implication for nanoscale molecule sensor [J]. The Journal of Physical Chemistry: C, 2008, 112(35): 13442-13446.
[7] LU G, OCOLA L E, CHEN J. Gas detection using low-temperature reduced graphene oxide sheets [J]. Applied Physics Letters, 2009, 94(8): 083111.
[8] XUE Y Q, DATTA S, RATNER M A. First-principles based matrix Green’s function approach to molecular electronic devices: general formalism [J]. Chemical Physics, 2002, 281(2/3): 151-170.
[9] ATACA C, AKTURK E,AHIN H, et al. Adsorption of carbon adatoms to graphene and its nanoribbons [J]. Journal of Applied Physics, 2011, 109(1): 013704.
[10]REICH S, MAULTZSCH J, THOMSEN C, et al. Tight-binding description of graphene [J]. Physical Review: B, 2002, 66(3): 035412.
[11]邓小清, 杨昌虎, 张华林. B/N 掺杂对于石墨烯纳米片电子输运的影响 [J]. 物理学报, 2013, 62(18): 186102. DENG Xiaoqing, YANG Changhu ZHANG Hualin. The electronic transport properties affected by B/N doping in graphene-based molecular devices [J]. Acta Physica Sinica, 2013, 62(18): 186102.
[12]李彪, 徐大海, 曾晖. 边缘重构对锯齿型石墨烯纳米带电子输运的影响 [J]. 物理学报, 2014, 63(11): 117102. LI Biao, XU Dahai, ZENG Hui. Influence of edge reconstruction on the electron transport in zigzag graphene nanoribbon [J]. Acta Physica Sinica, 2014, 63(11): 117102.
[13]IHNATSENKA S, KIRCZENOW G. Dirac point resonances due to atoms and molecules adsorbed on graphene and transport gaps and conductance quantization in graphene nanoribbons with covalently bonded adsorbates [J]. Physical Review: B, 2011, 83(24): 245442.
[14]ZHANG Y, CHEN Y, ZHOU K, et al. Improving gas sensing properties of graphene by introducing dopants and defects: a first-principles study [J]. Nanotechnology, 2009, 20(18): 185504.
(编辑 刘杨)
Electronic Transport Properties of Atom Adsorption Graphene Nanoribbon Devices Based on Tight Binding Green’s Function Method
LI Xin,ZHANG Yong,YIN Demin,WANG Xiaoli,LIU Weihua
(School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
Electron transport properties of four kinds of atoms H, F, O and OH to adsorb armchair graphene nanoribbons (AGNR) and zigzag graphene nanoribbons (ZGNR) device are studied by using the tight binding non equilibrium Green function method. The electronic structure of GNR is analyzed using the tight binding theory of π electron structure. The electronic interaction among adsorbed atoms and GNR carbon atoms is calculated based on the expansion shock theory. The current characteristics of GNR adsorbing atoms are calculated using the non equilibrium Green function. The results show that the adsorption of H atoms has the greatest impact on the AGNR device transport spectrum in four kinds of atoms and the adsorption of OH atoms increases 0.3 eV of band gap at an equilibrium state, and that the current from H atom adsorption is larger than that of the other atoms at a non equilibrium state, because H atom adsorption not only increases density of states near the bottom of the conduction band, but also introduces impurity energy level in the band gap directly. The current from H atoms in ZGNR is 1.5 times higher than that from AGNR and the current of H atomic adsorption in middle of GNR is higher than that of its edge. The results provide a theoretical basis for improving the sensitivity of graphene gas sensors and biosensors.
graphene nanoribbons; atomic adsorption; tight binding; Green’s function; transmission spectra
2014-08-09。
李昕(1968—),女,副教授;王小力(通信作者),男,教授,博士生导师。
国家自然科学基金资助项目(91123018,61172041,61172040);陕西省自然科学基金资助项目(2014JM7277)。
时间:2014-11-13
10.7652/xjtuxb201502007
TN304.9
A
0253-987X(2015)02-0037-06
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141113.1028.001.html

