采用三角形节点块处理无线传感器网络节点定位中节点翻转歧义的迭代方法

董恩清,刘伟,宋洋

(山东大学(威海)机电与信息工程学院,264209,山东威海)



采用三角形节点块处理无线传感器网络节点定位中节点翻转歧义的迭代方法

董恩清,刘伟,宋洋

(山东大学(威海)机电与信息工程学院,264209,山东威海)

针对最小二乘法在无线传感器网络的节点定位中产生的节点翻转歧义问题,提出了一种基于三角形节点块处理节点翻转歧义的迭代方法(OPD-IP-INB)。该方法首先采用基于正交投影的节点翻转歧义检测方法对网络中所需定位的节点进行检测,然后根据三角形节点块具有的稳定性,充分利用全网络的连通性信息,通过坐标变换采用逐次寻优性的迭代方法,对发生翻转歧义的节点进行定位处理。仿真结果表明:OPD-IP-INB方法可以很好地处理最小二乘法中的节点翻转歧义问题,而且提高了整个网络的定位精度;与最小二乘法相比,随着信标节点的减少,其定位精度可以提高3%～10%;随着测距误差的减小,其定位精度可以提高2%～7%。

无线传感器网络;节点定位;翻转歧义;正交投影

节点定位技术是无线传感器网络的重要支撑技术之一[1-3]。目前,节点定位方法一般分为基于测距的定位方法和距离无关的定位方法[4]。相对于距离无关的方法,基于测距的方法具有较高的定位精度。由于无线传感器网络的应用一般需要精确的节点位置信息[5-7],所以基于测距的节点定位更符合实际的应用需求。作为基于测距的方法之一,最小二乘法具有原理简单、定位精度高等优点,所以被广泛地使用。但是,最小二乘法在定位过程中会发生节点的翻转歧义问题,而且节点翻转歧义还可能产生雪崩效应,严重时能导致整个网络节点的定位失效。

目前已经有研究者提出了许多翻转歧义的检测方法,其中Liu等人提出的基于正交投影的检测方法[8]是目前检测效果较好的一种方法,该方法具有检测精度高、计算复杂度低的优点。

对检测出可能发生翻转岐义的节点,有2种处理手段,一种是非联合节点连通信息处理,另一种是联合多节点连通信息处理。文献[9]提出了一种消除歧义的优化定位策略,该策略是一种非联合节点连通信息处理方法,它是利用计算出的2个节点位置(真实点位置和节点翻转歧义位置)与其他邻居节点的相互通信关系来消除翻转歧义节点;文献[10]也是一种非联合节点连通信息处理方法,该方法通过分析、检测未知节点的邻居节点是否隐性共线来选出发生翻转歧义的节点,再对选出的节点采用消除方法来去除歧义节点。

Xiao等人提出了一种新的节点定位方法——迭代不变体合并(Iterative Inflexible Body Merging, IIBM)算法[11]。该算法是一种基于块拼接的定位算法,它将网络中的节点划分成许多个节点块,然后对每个节点块进行拼接定位。由于考虑了节点块可能存在的翻转歧义,所以该算法间接地处理了节点翻转歧义问题。但是,文献[11]算法采用了各种形状的节点块进行拼接,增加了定位中节点块的自身形变,这样就产生了多种形式的节点块翻转歧义问题,从而增加了处理的复杂度。

受到文献[11]迭代不变体合并算法的启发,根据三角形节点块具有的稳定性,并充分利用全网络的连通性信息,本文提出了一种基于三角形节点块的处理节点翻转歧义的迭代方法(after orthogonal projection detection, iterative processing method based on triangular node blocks, OPD-IP-TNB)。该方法是在本课题组所提出的基于正交投影的节点翻转歧义检测方法[9]的基础上,对网络中需要定位的节点进行检测,再用文献[11]提出的迭代方法处理节点翻转歧义。本文方法具有比较好的系统性和完整性,能够很好地处理网络中节点的翻转歧义问题,具有一定的实际应用价值。

1 节点翻转歧义

节点定位中的节点翻转歧义问题是指未知节点在利用邻居已知节点进行定位时,如果邻居节点共线或近似共线,则可能得到2个关于某一条直线成镜像关系的估计位置。假设未知节点P有3个邻居信标节点A、B、C,该未知节点到这3个邻居信标节点的测量距离分别为d1、d2、d3。分别以信标节点A和B为圆心,以测量距离d1和d2作圆,如图1所示,那么未知节点必定为2个圆交点P和P′中的一个,且这2个交点关于直线AB对称。

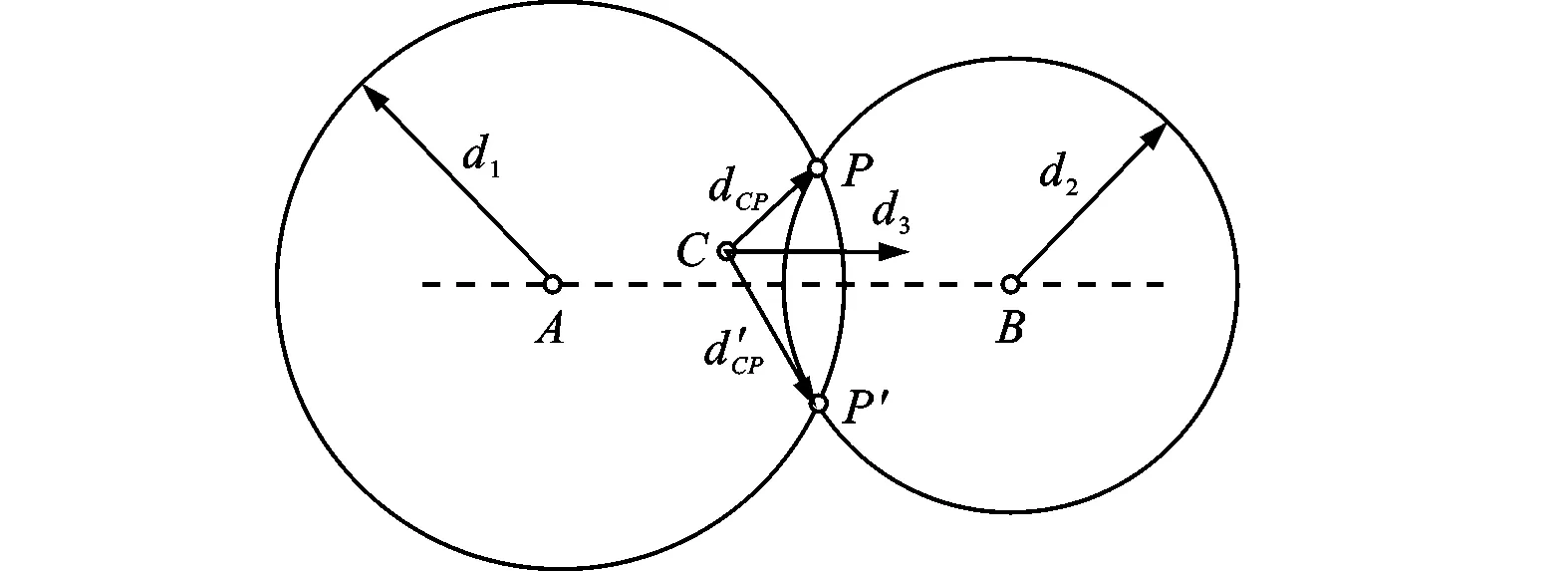
图1 节点翻转歧义示意图

假设所求未知节点的真实位置为P,信标节点C到P和P′的距离为dCP和dCP′。根据未知节点P到邻居信标节点C的测量距离d3来判断,dCP和dCP′中的哪一个与d3比较接近就选择哪一个为节点的定位位置。当A、B和C几乎共线时,dCP和dCP′相差不大,由于测距误差的存在,就有可能错误地将P′作为未知节点的定位位置,如果这种错误定位位置再参与其他未知节点的定位,将导致整个网络无法正确定位。

2 基于三角形节点块处理节点翻转歧义的迭代方法

2.1 迭代不变体合并算法

在迭代不变体合并算法[11]中,令2个节点块之间的约束集合为C={li},li=[mi,ni,di,ωi]。其中l表示约束,i表示约束的索引,mi表示信标节点块所在坐标系Φm中的节点坐标,ni表示未知节点块所在坐标系Φn中的节点坐标,di表示mi与ni的测量距离,ωi为测量距离的约束权重。

根据上面的定义,迭代不变体合并算法就是构建一个坐标变换方程和误差约束方程如下

TP,R(p*)=P+Rp*

(1)

ei(TP,R)=ωi(di-‖pi-TP,R(p*)‖)

(2)

式中:ei(TP,R)表示第i个约束的转换误差;P表示转换变量;p*表示节点块所在坐标系Φn中的节点坐标;R表示旋转变量矩阵;pi表示信标节点块所在坐标系Φm中的节点坐标。迭代不变体合并算法是构建一个目标函数,如下式所示

(3)

式中:|C|表示约束集C的个数。

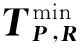
迭代不变体合并算法的主要计算步骤如下。

(1)已知约束集C,选取算法迭代的初始变量值P、R。

(2)给定时刻t的初始值,通过式(4)和式(5)来求得t+1时刻的P、R值,如此反复迭代更新P、R值,即

(4)

(5)

式中

(6)

(7)

式中:δ表示迭代步长;M表示未知节点块中的节点数(本文基于三角形节点块方法,M为3);Rrod表示罗德里格旋转矩阵;TP(t),R(t)表示t时刻的坐标转换矩阵。

迭代不变体合并算法把将节点定位过程类比为弹簧受力,最终达到平衡的过程。它将每个约束集Ci中的2个节点看作被一个弹簧相连,式(7)中的Fi(t)相当于第i个约束施加在弹簧上的力。式(6)中的F(t)则表示所有的约束施加在弹簧上的合力。

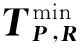
(8)

式中:P(t+n)和R(t+n)表示t+n时刻的P、R值;ε为一很小的正数。

2.2 三角形节点块迭代处理方法

当节点定位过程可能发生翻转歧义时,处理翻转歧义的主要方法就是利用网络中更多的其他节点信息来参与定位。基于这种思想,对可能发生翻转歧义的节点找到其所有的邻居非信标节点,然后在这些邻居非信标节点中每次选出3个节点(其中必须含有本次所需定位的未知节点)构成一个三角形节点块。

假设所求未知节点P有3个邻居信标节点B1、B2、B3,用集合Ω1来表示;S、Q、U、V、M、N为P点的邻居非信标节点,用集合γ来表示;B4,B5,B6,…为集合γ中节点的邻居信标节点,用集合Ω2表示。首先,对未知节点P定位时进行正交投影检测,判断出该节点可能会发生节点翻转歧义。然后,将未知节点P与集合γ中的任意2个节点组成多个不同的三角形节点块,此处仅列举出4个三角形节点块,如图2中的三角形节点块PSQ、PUV、PSM和PVN所示。

图2 三角形节点块示意图

在找到包含未知节点P的多个三角形节点块之后,构建2个坐标系,此处以三角形节点块PSQ为例进行说明。将三角形节点块PSQ的所有邻居信标节点所在的坐标系记为Φm,由未知节点P、S、Q构成的三角形节点块所在的坐标系记为Φn。通过采用迭代不变体合并算法的坐标变换公式(本文中约束误差方程中的系数ωi取为1),求出三角形节点块的坐标。

基于三角形节点块迭代处理方法,首先使用文献[9]中的基于正交投影的方法对未知节点进行翻转歧义检测,如果检测后节点不会发生翻转歧义,那么仍旧采用最小二乘法进行定位。如果检测后节点可能会发生翻转歧义,那么采用本文方法进行处理。

本文提出的基于三角形节点块迭代方法的计算复杂度和三角形节点块的数量有关,也就是与未知节点的邻居非信标节点的数量有关。假设未知节点的邻居非信标节点的个数为k。由于任意2个未知节点的邻居非信标节点都可以和该未知节点组成一个三角形节点块,所以本文方法的计算复杂度为O(k2)。由此可见,当未知节点的邻居非信标节点的数量较大时,本文方法的计算复杂度较高。不过一般来说,未知节点的邻居非信标节点的数量越大,则网络的连通度越大,未知节点发生翻转歧义的概率则越低,因此这种情况下处理翻转歧义的概率也越低。本文提出的基于三角形节点块迭代方法在使用过程中,主要遇到的还是未知节点的邻居非信标节点的数量较小时的情况,而此时算法的计算复杂度并不大。

本文利用了上文2.1节迭代不变体合并算法的坐标变换公式,但在计算处理过程中与迭代不变体合并算法有明显区别。

2.2.1 网络中处理的节点数量差异 在迭代不变体合并算法中,所有未知节点的定位均采用块拼接的思想方法,而本文的迭代处理方法只是处理正交投影检测后可能发生翻转歧义的那部分节点,对不会发生翻转歧义的节点仍采用最小二乘法。由于迭代不变体合并算法利用了块拼接方法的优点,即可以充分利用网络的信标节点信息,所以该方法可以定位的节点数量较大,但定位精度不高。本文基于三角形节点块迭代的处理方法是以最小二乘法为基础的,首先通过正交投影检测法进行翻转歧义节点的检测,因此处理的节点数由正交投影检测后可能发生翻转歧义的节点数决定。

2.2.2 算法中节点块存在形状差异 迭代不变体合并算法中的节点块具有多种形状。随着节点块所含节点数的增多,节点块的形状有更多的变化,因此定位中就需要考虑节点块的更多变化位置。一般情况下,这将会产生更多的节点块翻转歧义,增加节点块变化的复杂性。本文所采用的节点块只是三角形节点块,是选取可能会发生翻转歧义的未知节点与其邻居非信标节点所能构成的三角形节点块,使得每个三角形节点块均由未知节点所构成。此外,迭代不变体合并算法中节点块之间可以共享一个或多个节点(如图2中节点P既是Ω1中的节点,又是γ中的节点),而本文中的三角形节点块与由信标节点构成的节点块之间只是靠测量距离的边连接(如图2中三角形节点块PSQ和其邻居信标节点B1,B2,B3,…所构成的节点块之间是靠彼此间的相互通信进行连接的)。

2.2.3 算法的迭代处理步骤差异 迭代不变体合并算法的主要步骤是:首先将网络中满足一定约束条件的2个节点块进行拼接定位,其他节点块再与上述的节点块继续进行块拼接定位,这样使得节点块的容量(含有节点的数量)不断增加。在整个的定位过程中,迭代不变体合并算法是将成功定位的节点转化为新的信标节点参与其他节点块的拼接过程,而本文方法则是对每个三角形节点块(如图2中的节点块PSQ、PUV、PSM和PVN等)都进行坐标变换的迭代计算,并且可以保证所有的三角形节点块的迭代处理过程互不干扰,即每一个三角形节点块的迭代处理过程不受上一次三角形节点块迭代处理过程的影响。此外,本文中迭代处理方法只利用了网络中的信标节点信息,因此不会引入累积误差。本文方法的缺点是需要更多的参考节点,而且网络规模较大时,计算会比较复杂。因此,本文方法在网络规模较小时能发挥更好的作用。

迭代不变体合并算法主要是对整个网络中的节点块进行拼接定位。该算法优先对包含信标节点的节点块进行拼接,再对不包含信标节点的节点块进行拼接,并且该算法对节点块的拼接顺序也有选择性要求,具体表现为:在整个网络节点块的拼接过程中,节点块根据节点块的约束度(Degree-of-Constraint, DOC)与节点块的自由度(Degree-of-Freedom, DOF)差值由大到小的顺序进行拼接。本文所采用的策略以图2所示为例加以表述。首先,找出包含所求未知节点P构成的所有三角形节点块,如节点块PSQ、PUV、PSM和PVN等(本文仅以三角形节点块PSQ为例进行说明),并且将节点S、Q的邻居信标节点用集合Ω3来表示;其次,判断集合Ω3中的元素与集合Ω1中不同元素的数量,如果其数量在1～5之间,那么此三角形节点块PSQ就正常参与迭代计算,否则不参与迭代计算;最后,对所有三角形节点块均采用上述的处理方法,将满足条件的三角形节点块正常参与迭代计算,这样就可以保证所选取的三角形节点块能够最大限度地利用更多不同的邻居信标节点信息来参与定位。

2.3 采用邻居节点信息的三角形节点块修正

在基于三角形节点块处理节点翻转歧义的迭代方法中,会出现一些严重影响算法定位精度的三角形节点块特例,因此本文提出加入基于正交投影检测判别模块和邻居节点信息检测模块,以去除这些严重影响算法精度的三角形节点块,完善基于三角形节点块处理节点翻转歧义的迭代方法。

图3～图6列出了几种严重影响本文迭代处理方法定位精度的特殊三角形节点块PSQ。

图3 块中未知节点的邻居信标节点与另外2个节点近似共线

图4 块中3个节点的邻居信标节点近似共线

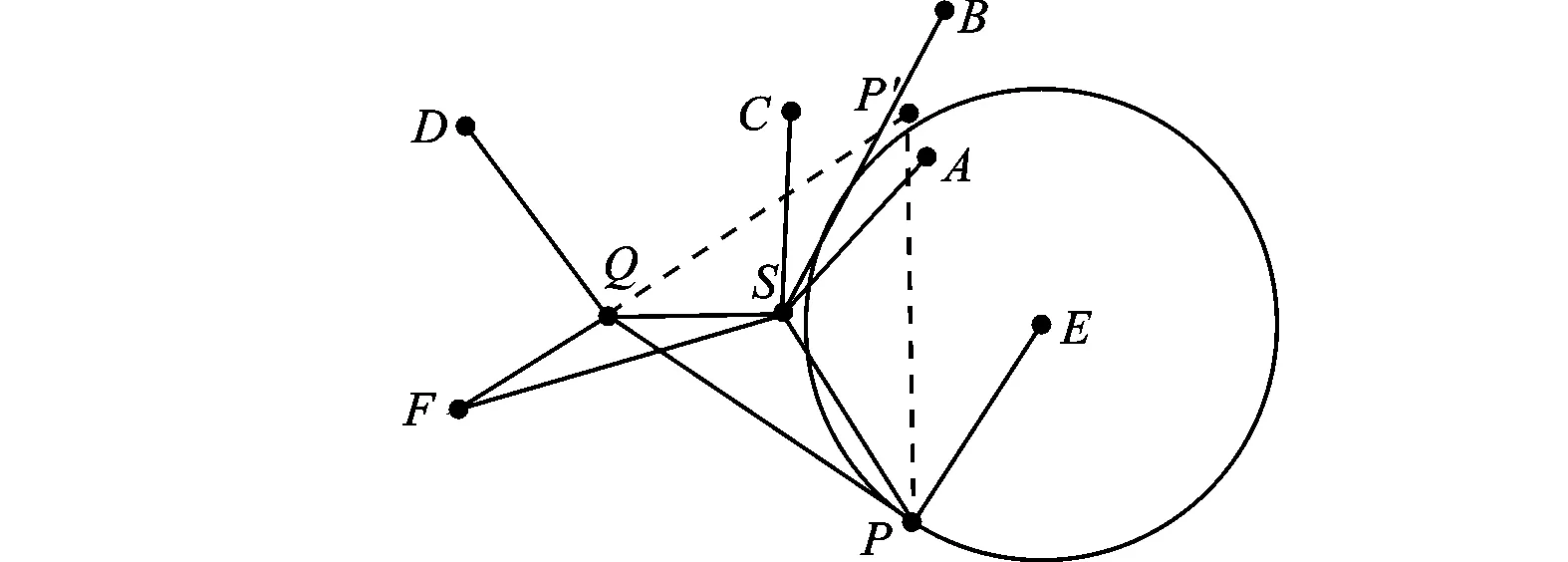
图5 块中未知节点没有足够邻居信标节点

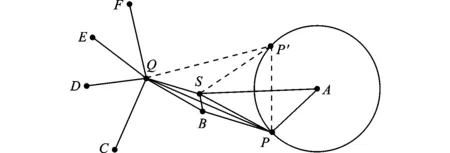
图6 块中3个节点近似共线

图3和图4是所求未知节点P具有大于等于3个邻居信标节点的情况。图3中所选三角形节点块中的其他2个未知节点Q、S与节点P的邻居信标节点近似共线。图4中所选三角形节点块PSQ的所有邻居信标节点近似共线。

图5和图6是未知节点P没有足够邻居信标节点的情况。经分析可知图5是图3的一种特例情况,它表示所求未知节点P没有足够邻居信标节点。图6中所选三角形节点块中的3个顶点近似共线。由于节点间的测量距离受测距误差的影响,所以当选取的三角形节点块PSQ存在如图3～图6所示的几种特殊情况时,本文提出的处理节点翻转歧义的迭代方法会产生很大的定位误差,应给予排除。因此,利用本文基于三角形节点块的迭代处理方法时,需要对所使用的三角形节点块加入一定的限制约束条件,其主要修正步骤如下。

(1)利用正交投影检测法对所选取的三角形节点块进行判断。如果存在一条直线与以节点P、Q、S为圆心,以测距误差为半径的误差圆相交,则这样的三角形节点块将不会参与迭代处理方法。

(2)如果所选三角形节点块的3个节点利用步骤(1)的方法进行判断后不近似共线,那么就采用文中提出的迭代处理方法计算出所选取三角形节点块的估计坐标。

(3)分别对步骤(2)中所得的若干三角形节点块的估计坐标,按照下面准则进行邻居节点信息检测判断。以所得未知节点定位位置坐标为圆心,以节点的通信半径作圆、判断该圆内是否存在实际不与该节点通信的其他节点。如果存在这样的节点,那么就对该估计坐标予以删除处理。

3 仿真实验分析

为了验证本文提出的OPD-IP-INB方法的性能,采用仿真实验进行分析。仿真实验参数如表1所示。

表1 网络参数的配置

3.1 信标节点数对处理翻转歧义效果的影响

不同的信标节点数决定最小二乘法中节点发生翻转歧义的可能性,并直接影响着节点的定位精度。因此,本文通过模拟仿真来验证各种处理节点翻转歧义效果与信标节点数的变化关系。仿真的测距误差假设是一个均值为0、方差为0.15的高斯白噪声。

下面采用3种定位方法与本文方法进行比较,其中:OPD-LS(after using orthogonal projection detection, least squares)表示正交投影检测后用最小二乘法进行定位的方法;OPD-PSO(after using orthogonal projection detection, particle dwarm optimization)表示正交投影检测后用PSO算法进行定位的方法;IIBM(iterative inflexible body merging)表示用迭代不变体合并算法进行定位的方法;OPD-IP-TNB为本文定位方法。采用4种方法对不同信标节点数的仿真结果如图7所示。

(a)定位误差曲线

(b)定位数曲线图7 4种算法对不同信标节点数的仿真结果

从图7中可以看出:本文方法在定位误差和定位节点数2个方面均优于OPD-PSO方法;尽管在定位节点数方面,本文方法不如IIBM方法和OPD-LS方法,但是本文方法可以明显提高节点的定位精度,而且在信标节点数较少时,提高得更明显。因此,本文方法对于处理最小二乘法中节点翻转歧义具有明显的优势。

图8和图9分别为最小二乘法(least squares,LS)和本文OPD-IP-TNB方法在处理节点翻转歧义时所能达到的节点定位精度和定位节点数。由图9可以看出,在利用最小二乘法进行网络中的节点定位时,确实存在节点翻转歧义问题。根据本文模拟仿真的参数设置,并由图9中可能发生节点翻转歧义的数目柱状图可知,在节点定位中可能发生翻转歧义的节点数大约为10～12。此外,由图8可以明显得出结论,IP-TNB处理方法比LS处理方法效果要好,可以大幅减小定位误差,提高定位精度,随着信标节点数的减小,定位精度可以提高3%～10%。

图8 本文方法与LS方法处理翻转歧义后的定位误差

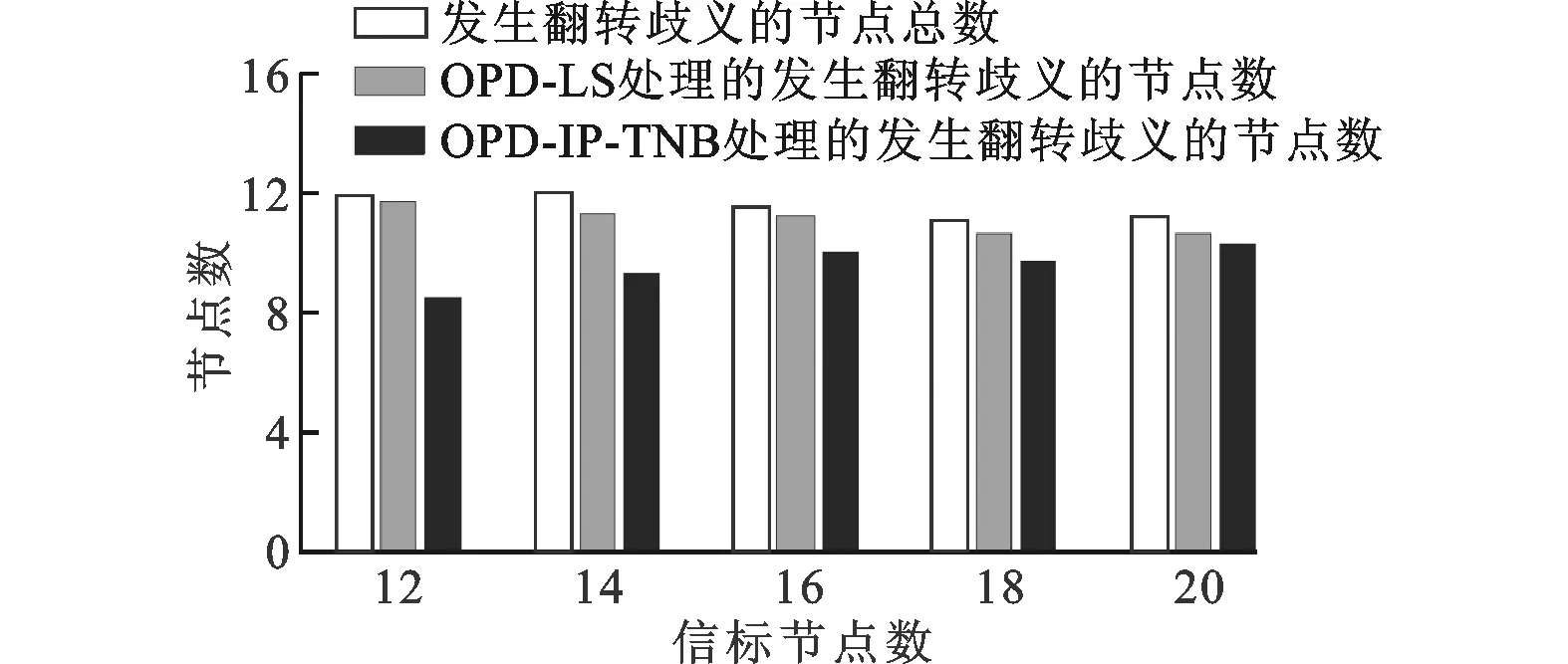
图9 本文方法与LS方法处理翻转歧义后的节点数

3.2 测距误差对处理翻转歧义效果的影响

无线传感器网络节点间的测距误差直接决定节点发生翻转歧义的概率,并最终关系到整个网络的定位精度。所以,文中通过模拟仿真实验来验证测距误差对OPD-IP-TNB方法性能的影响。本次仿真中信标节点数是15。

不同测距误差的仿真结果如图10所示。由图10可以看出,本文OPD-IP-TNB方法在定位误差和定位节点数2个方面均优于OPD-PSO方法,尽管在定位节点数方面,本文方法不如IIBM方法和OPD-LS方法,但是本文方法可以明显提高节点的定位精度。

(a)定位误差曲线

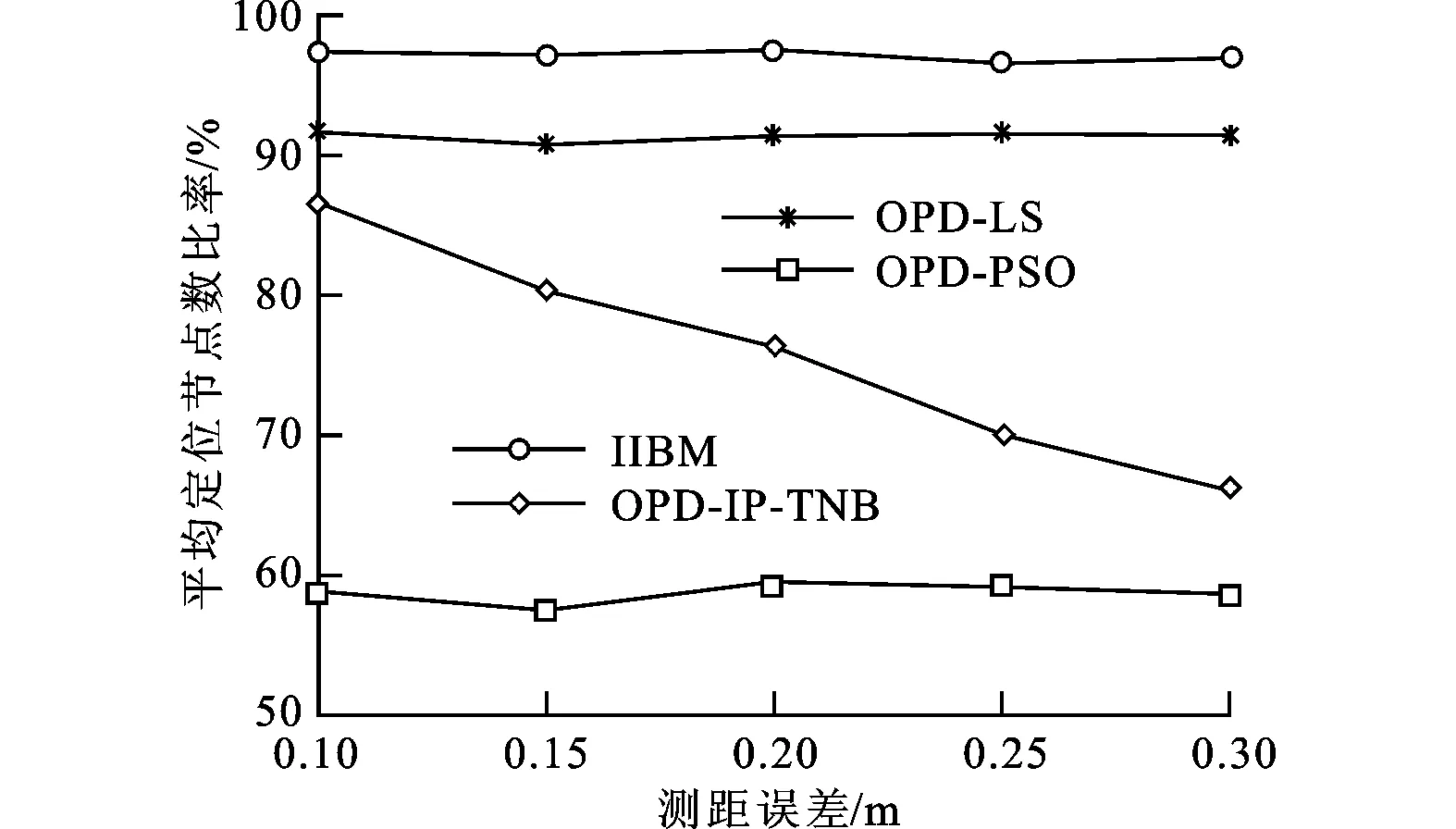
(b)定位数曲线图10 不同测距误差下的仿真结果

本文方法的缺点是其受测距误差的影响比较敏感,当测距误差较大时,其能够定位的节点数急剧下降,因此本文方法只适用于测距误差较小的情况。

图11和图12分别表示2种方法处理节点翻转歧义的定位精度和数量。从图12的柱状图可以明显看出,随着测距误差的增大,网络中节点发生翻转歧义的数量不断增加。与最小二乘法相比,虽然文中的迭代方法处理节点翻转歧义的数量稍微有减少,但从图11中可以看出本文的方法可以明显提高处理节点翻转歧义的定位精度,随着测距误差的减小,定位精度可以提高2%～7%左右,即可以有效地修正翻转歧义节点。

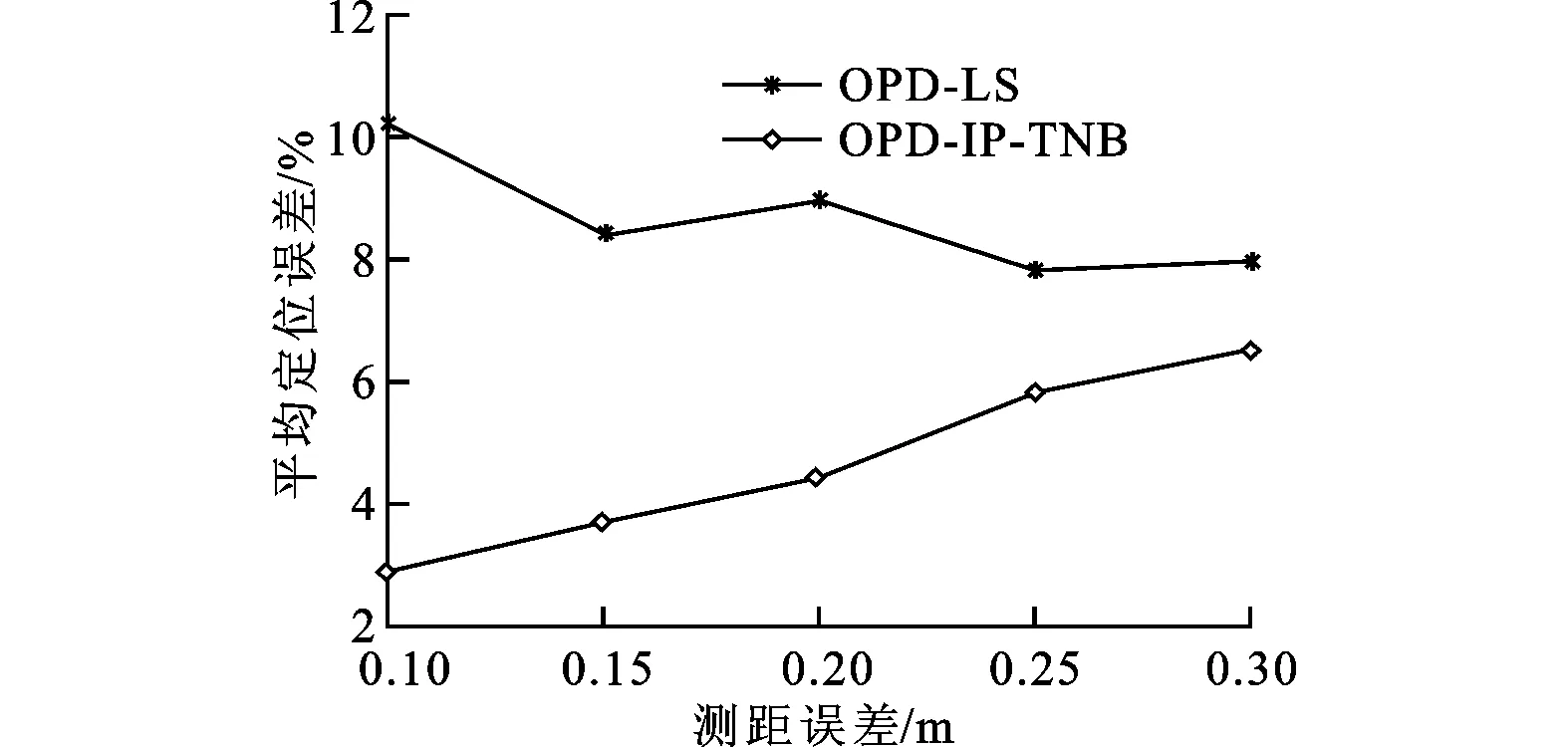
图11 不同测距误差下处理翻转歧义后的定位误差

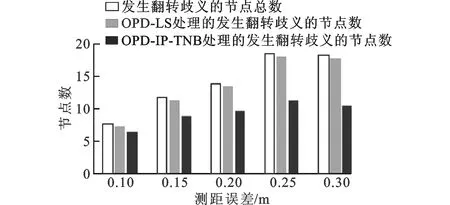
图12 不同测距误差下处理翻转歧义节点数的对比

4 结 论

本文提出了一种基于三角形节点块的迭代方法处理节点翻转歧义。该方法首先采用正交投影检测,找出定位中可能发生翻转歧义的节点,然后采用坐标变换逐次寻优性的迭代方法对发生翻转歧义的节点进行处理。仿真分析说明,本文提出的方法可以很好地处理最小二乘法中的节点翻转歧义问题,提高了节点的定位精度。然而,本文方法对测距误差比较敏感,当测距误差比较大时,本文方法虽然也可以处理节点翻转歧义问题,但要牺牲很大一部分节点定位数,因此还需要对该方法做进一步的研究。

[1]SALMAN N, GHOGHO M, KEMP A H.Optimized low complexity sensor node positioning in wireless sensor networks [J].IEEE Sensors Journal, 2014, 14(1):39-46.

[2]VEMPATY A, OZDEMIR O, AGRAWAL K, et al.Localization in wireless sensor networks:Byzantines and mitigation techniques [J].IEEE Transactions on Signal Processing, 2013, 61(6):1495-1580.

[3]JIANG J A, ZHENG X Y, CHEN Y F, et al.A distributed RSS-based localization using a dynamic circle expanding mechanism [J].IEEE Sensors Journal, 2013, 13(10):3754-3766.

[4]GUO Z W, GUO Y, HONG F, et al.Perpendicular intersection:locating wireless sensors with mobile beacon [J].IEEE Transactions on Vehicular Technology, 2010, 59(7):3501-3509.

[5]董恩清, 邹宗骏, 张德敬, 等.基于动态路径列表的无线传感器网络时间同步协议 [J].光学精密工程, 2013, 21(11):2951-2959.DONG Enqing, ZOU Zongjun, ZHANG Dejing, et al.Time synchronization protocol based on dynamic route list for wireless sensor network [J].Optics and Precision Engineering, 2013, 21(11):2951-2959.

[6]CENEDESE A, ORTOLAN G, BERTINATO M.Low-density wireless sensor networks for localization and tracking in critical environments [J].IEEE Transactions on Vehicular Technology, 2010, 59(6):2951-2962.

[7]汪志伟, 曹建福, 郑辑光.一种面向分簇无线传感器网络的多信道跨层协议 [J].西安交通大学学报, 2013, 47(6):61-67.WANG Zhiwei, CAO Jiaufu, ZHENG Jiguang.Multi-channel multi-path cross-layer protocol for clustered wireless sensor networks [J].Journal of Xi’an Jiaotong University, 2013, 47(6):61-67.

[8]LIU W, DONG E Q, SONG Y, et al.An improved flip ambiguity detection algorithm in wireless sensor networks node localization [C] ∥Proceedings of 2014 International Conference on Telecommunications.Piscataway, NJ, USA:IEEE, 2014:206-212.

[9]WANG X P, LIU Y H, YANG Z, et al.OFA:an optimistic approach to conquer flip ambiguity in network localization [J].Computer Networks, 2013, 57(6):1529-1544.

[10]BU K, XIAO Q J, SUN Z X, et al.Toward collinearity-aware and conflict-friendly localization for wireless sensor networks [J].Computer Communications, 2012, 35(13):1549-1560.

[11]XIAO Q J, XIAO B, BU K, et al.Iterative localization of wireless sensor networks:an accurate and robust approach [J].IEEE/ACM Transactions on Networking, 2014, 22(2):608-621.

(编辑 刘杨)

An Iterative Method for Using Triangular Node Blocks to Process Node Flip Ambiguity of Node Localization in Wireless Sensor Networks

DONG Enqing,LIU Wei,SONG Yang

(School of Mechanical, Electrical & Information Engineering, Shandong University, Weihai, Shandong 264209, China)

An iterative method based on triangular node blocks (OPD-IP-TNB) is proposed to solve the problem of the node flip ambiguity generated in using least squares method to locate nodes in wireless sensor networks.First, the orthogonal projection detection method is adopted to detect unknown nodes to be positioned.Then the iterative method based on coordinate transformation and recursive optimization is applied to process the flip ambiguity nodes by using the stability of triangle node blocks and the whole network connectivity information.Simulation results show that the proposed method can effectively deal with the node flip ambiguity in using the least squares method, and improve localization accuracy of the whole network.Comparison with the least squares method shows that the localization accuracy improves by 3%-10% when the number of anchor nodes decreases, and by 2%-7% when the range errors decreases.

wireless sensor networks; node localization; flip ambiguity; orthogonal projection

2014-08-29。 作者简介:董恩清(1965—),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(81371635);教育部高等学校博士学科点专项科研基金资助项目(20120131110062);山东省科技发展计划资助项目(2013GGX 10104)。

时间:2015-01-16

http:∥www.cnki.net/kcms/detail/61.1069.T.20150116.1510.001.html

10.7652/xjtuxb201504014

TP212;TN92

A

0253-987X(2015)04-0084-07