基于渐消记忆滤波的弹道修正弹落点预测*
李超旺,高 敏,方 丹,卢志才
(解放军军械工程学院,石家庄 050003)
基于渐消记忆滤波的弹道修正弹落点预测*
李超旺,高敏,方丹,卢志才
(解放军军械工程学院,石家庄050003)
摘要:针对滤波处理所需时间长、准确建立误差模型难的问题,提出了仅对弹道落点预测偏差进行滤波的方法,给出了弹道方程及落点预测方程。关于弹道修正弹飞行过程中弹道经常发生突变及弹载计算机运算能力有限的问题,提出了基于渐消记忆滤波的自适应滤波方法,采用半实物仿真试验和飞行试验对该滤波方法进行了试验验证,结果表明该方法能实现实时滤波,弹道突变时滤波后的预测偏差可保持相对平滑,没有引起发散现象,实用性很强。
关键词:弹道修正弹;渐消记忆滤波;全球定位系统;落点预测
0引言
弹道修正弹具有较高的作战效费比,是世界各国争相研究的热点。如何精确测量弹道参数及如何预测落点偏差是弹道修正控制系统设计中的重要问题。GPS具有绝对定位精度高、误差不随时间累积的优点,可用于弹道修正弹弹道参数的测量。然而,由于GPS信号存在信号较弱,易受干扰,随机误差大的缺点,直接使用不加处理的GPS信号进行导航将影响射击精度。
采用最小二乘法可以在很大程度上消除随机误差影响[1],但由于其未与弹道方程结合,使得计算量大导致实时性变差。卡尔曼滤波适用于线性系统,为了提高滤波精度,需要建立较为准确的系统模型和观测模型[2-5],然而造成GPS定位随机误差的误差源很多,对随机误差进行准确建模是不现实的,此外,系统模型和观测模型多是非线性的,采用卡尔曼滤波方法进行滤波时增加了计算量,对滤波效果的改善是有限的。
1落点预测算法
1.1 弹道方程
弹道修正弹工作原理是[4]:在弹箭发射前,根据目标信息计算出基准弹道,弹箭出炮口后测量系统实时测量出实际弹道参数,通过和基准弹道的比较预测出弹道落点偏差,形成控制指令,控制执行机构作用来进行弹道修正。
由弹道修正弹的工作原理可知,弹箭发射前需要根据火炮和目标点坐标、弹箭总体参数、弹箭气动系数和气象信息计算基准弹道。考虑到弹道修正弹修正能力有限,对于基准弹道的精度要求较高,以122 mm火箭弹为例建立了六自由度弹道方程[6]。
(1)
式中:x、y、z、Vx、Vy、Vz分别为弹箭在发射坐标系中的坐标分量和速度分量;Fx、Fcx、Frkx、Rx、gx、acx、aex分别表示发动机推力、控制力、燃气流动的科氏惯性力、气动力、重力加速度、科氏加速度和牵连加速度在发射坐标系中x轴方向上的分量。
发动机推力为:
(2)
式中:F(Tt)为随装药温度变化的发动机静态推力;Sa为火箭弹发动机喷口面积;PH为不同高度的大气压强;PH0为发动机静态试车的环境大气压力。
(3)
式中:q为火箭弹的动压;S为火箭弹参考面积;C为气动系数。
(4)
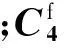
当需要进行弹道修正时,将Fc引入到弹道方程里面。气动系数采用查表线性插值的方法计算得出,利用四阶龙格-库塔法进行弹道积分计算基准弹道。
1.2 落点预测方程
由弹道修正弹的工作原理可知:对弹箭进行控制之前需要进行落点偏差预测,当落点偏差大于一定范围时进行弹道修正。针对弹道修正弹控制系统对于落点预测的精度要求较高、实时性强的特点,提出采用一种基于摄动原理[7]的落点预测方法。
在确定基准弹道以后,可以根据摄动原理对预测偏差系数进行计算,飞行中将弹道偏差与相应的偏差系数相乘得出相应的落点偏差。
设发射前由式(1)计算的射程x0处的基准弹道参数为Vx0、Vy0、y0、Vz0、z0。

火箭弹飞行过程中GPS接收机输出的定位信息转换到发射系内的实际弹道参数为xG、yG、zG、VxG、VyG、VzG。
当x0=xG时,对应的弹道参数偏差为:
(5)
则射程x0处的落点预测偏差为:
(6)
(7)
式中ΔL为纵向预测偏差,ΔH为横向预测偏差。
飞行中以射程为自变量,对基准弹道参数和预测偏差系数进行线性插值,由式(4)~式(6)实时计算落点偏差。
2渐消记忆滤波算法
渐消记忆滤波器[8]是一种常值增益滤波器,采用递归的形式对输入信号进行估计,将不同时刻的测量数据赋以不同的权重,保证了对最新测量数据的利用,同时也考虑了旧数据的作用,具有计算量少,数值稳定性好,所需调节参数少等优点,是卡尔曼滤波器等高级滤波器的基础。它只用信号的前一个估计值和最近观察值就可以在线性无偏最小方差准则下估计信号的当前值。渐消记忆滤波的普遍公式为:
一阶渐消记忆滤波器:
(8)
二阶渐消记忆滤波器:
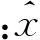
从式(8)、式(9)可以看出,应用渐消记忆滤波算法的最关键因素在于阶数的选择及增益因子的选取。
2.1 渐消记忆滤波器阶数的确定
考虑到落点预测对于滤波算法实时性的要求,对一阶、二阶渐消记忆滤波器进行对比分析。通过GPS信号模拟器引入GPS测量噪声,形成模拟的GPS量测数据,当增益因子β=0.8时,一阶和二阶渐消记忆滤波算法对落点预测偏差的滤波效果如图1所示。
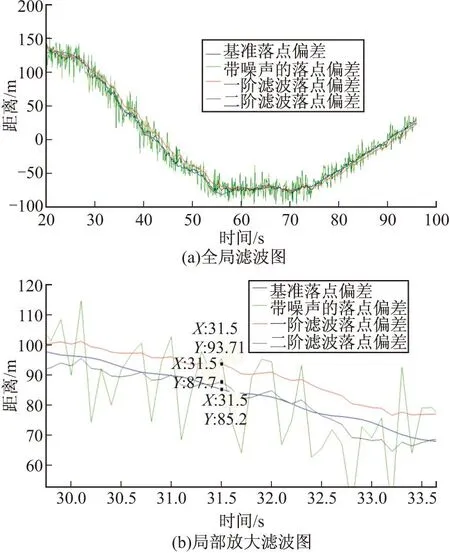
图1 一阶、二阶渐消记忆滤波效果图
从图1可以看出,一阶、二阶渐消记忆滤波算法对预测落点偏差均具有滤波效果,一阶滤波曲线较二阶滤波曲线平滑,但一阶滤波后的预测偏差曲线与基准落点偏差曲线差别较远,二阶滤波后预测曲线与基准落点偏差曲线更为接近,均方误差更小。以31.5 s时落点预测偏差为例,一阶滤波后的偏差为8.5 m,而二阶滤波后偏差为2.5 m,二阶滤波精度相对于一阶滤波提高了70.6%,二阶滤波较一阶滤波具有明显的精度优势。
综合考虑落点预测精度和实时性要求,确定采用二阶渐消记忆滤波器对落点偏差预测进行滤波处理。结合式(5)、式(6)及式(9)可得预测落点纵向和横向偏差的滤波分别为:
式(10)、式(11)中的下标n、n-1分别表示当前值、上一步值。
2.2 增益因子的选择
通常情况下增益因子为单一固定常数,经验取值在0.8~1.0之间,增益因子的选择范围确保了滤波后的收敛性。
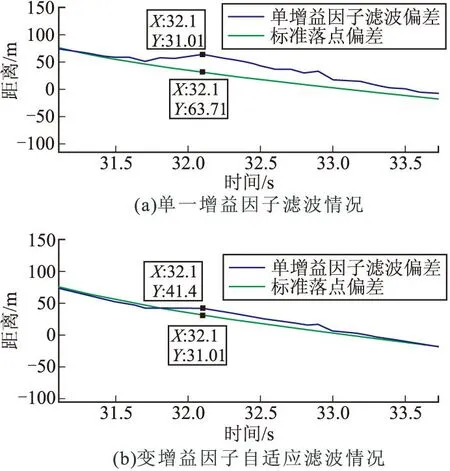
图2 单一、变增益因子自适应滤波效果
仿真分析中发现,采用单一增益因子,当偏差值大于一定范围时,滤波效果变差。针对这种情况,提出了采用变增益因子的自适应滤波算法,当偏差值在一定范围以内时,采用某一增益因子,而当预测偏差大于这一范围时采用另一增益因子。增益因子取值以滤波后方差最小为原则计算取得。采用式(12)所确定的预测偏差范围和增益因子进行了滤波仿真试验,试验结果如图2所示。
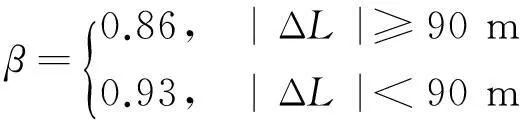
(12)
从图2可以看出,采用单值增益因子情况下32.1 s时刻滤波后的值较标准值偏32.6 m,而采用变增益因子之后该时刻的滤波后的偏差值减小到10.39 m,滤波精度明显提高。
3半实物仿真试验及飞行试验
3.1 半实物仿真试验
为验证上述算法对落点预测滤波的实时性和精确性,以122 mm火箭弹发射为例,进行了半实物仿真试验。仿真试验利用GNS-8440多体制导航信号模拟器和高动态C/A码接收机,模拟弹丸实际飞行时卫星定位测量情况,弹载控制器根据GPS数据和基准弹道来预测偏差并形成控制指令,控制脉冲推冲器作用。接收机水平定位精度为8 m(1σ),垂直定位精度为15 m(1σ),水平定速精度为0.3 m/s(1σ),垂直定速精度为0.4 m/s(1σ),式(13)、式(14)为纵向、横向预测偏差范围及对应的增益因子。
(13)
(14)
假设GPS采样定位时间间隔为0.1 s,火箭弹发射20 s后开始根据预测偏差情况进行脉冲修正控制。模拟仿真过程中预测偏差滤波前后对比情况如图3所示。
从图3可以看出,由于GPS接收机定位精度和测量误差的存在,横向和纵向预测偏差值跳动较大,经滤波后这种波动幅度明显减小,滤波效果明显。从图3(a)可以看出,20~50 s时间段内横向预测偏差为70 m左右,50 s开始进行连续的弹道修正,图中明显可见落点预测偏差值发生了突变,采用渐消记忆自适应滤波方法后预测偏差能够平稳过渡,没有出现滤波发散现象,滤波收敛较快,纵向预测偏差具有同样的滤波效果。此外,试验结果表明滤波计算时间为纳秒级,远小于弹载控制器的控制周期(毫秒级),实现了实时滤波。
3.2 飞行试验分析
为验证算法的有效性,加工了样品弹及控制执行机构,采用渐消记忆自适应滤波方法进行了二维弹道修正火箭弹的飞行试验。为了了解和掌握飞行控制具体情况,在样品弹上搭载了记录仪,记录仪记录的横向、纵向滤波前后的预测偏差情况如图4所示。
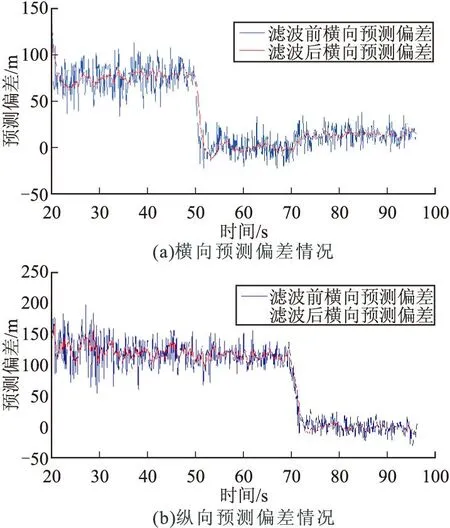
图3 仿真试验预测偏差滤波前后对比图
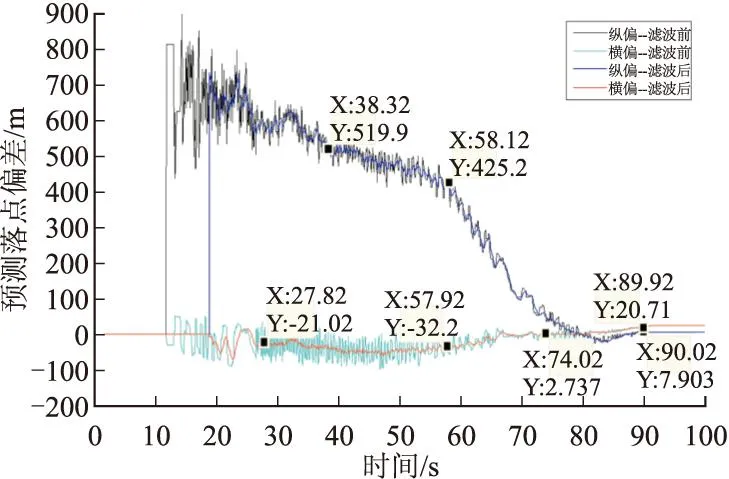
图4 飞行试验落点预测滤波前后对比图
从图4可以看出11 s左右弹箭进行初始定位,根据GPS信号和装定数据开始进行落点偏差预测,由于定位、定速误差的存在及随机性,预测值跳动较大,图中可见某些点与相邻点之间的预测值相差达300多米,很显然这是不正确的,需要进行滤波处理。按照控制方案设计要求,19 s左右开始进行落点预测及滤波处理,图中明显可见滤波效果,横向预测偏差基本为0 m,横向不需要进行修正,而纵向预测偏差较大,20 s左右预测偏差为700 m。根据预测偏差情况及控制方案设计要求,58.12 s开始进行纵向修正,纵向预测偏差值逐渐向目标点收敛,收敛过程中滤波后的值没有出现发散现象,滤波后预测偏差平稳收敛。最终实际落点在发射系内与目标点相比偏近11.1 m,偏右19.0 m,再次验证了方法的有效性。
4结论
基于摄动原理提出了将GPS接收机输出的定位
信息直接用于弹道落点预测,仅对落点预测进行滤波的方法。针对弹道修正弹飞行过程中弹道经常发生突变及弹载计算机运算能力有限的问题,提出了基于渐消记忆滤波的自适应滤波方法。采用半实物仿真试验和飞行试验对所提方法进行了验证,试验结果表明,该方法能实现实时滤波,弹道发生突变时,滤波值没有出现发散现象,精确度较高,可用于弹道修正弹的落点预测及弹道控制系统设计。弹道开始阶段纵向预测存在一定的偏差,还应该做进一步的研究。
参考文献:
[1]申强, 葛腼, 张冀兴, 等. 一种GPS弹道辨识方法的精度仿真分析 [J]. 北京理工大学学报, 2009, 29(2): 100-102.
[2]Thomas Recchia. Projectile velocity estimation using aerodynamics and accelerometer measurements: A kalman filter approach[R]. U.S. Army ARDEC,METC, 2010.
[3]李岩, 任睿, 王旭刚, 等. 两种卡尔曼滤波模型在修正弹弹道数据处理中的应用比较 [J]. 弹道学报, 2011, 23(1): 27-30.
[4]丁传炳, 王良明, 常思江, 等. 卡尔曼滤波在GPS制导火箭弹中的应用 [J]. 南京理工大学学报, 2010, 34(2): 157-160.
[5]Yoshio Kosuge. Non-process-noise tracking filter using a constant velocity model [C]∥SICE Annual Conference, 2008.
[6]杨绍卿. 火箭外弹道偏差与修正理论 [M]. 北京: 国防工业出版社, 2011.
[7]陈世年. 固体弹道导弹系列控制系统设计 [M]. 北京: 宇航出版社出版, 1996.
[8]Paul Zarchan. Tactical and strategic missile guidance [M]. American Institute of Aeronautics, Inc. 1997.
收稿日期:2014-03-19
作者简介:李超旺(1985-),男,山东济宁人,博士研究生,研究方向:弹药智能化与信息化。
中图分类号:TJ012.3
文献标志码:A
Fading Memory Filter-based Impact Point Prediction of
Trajectory Correction Projectile
LI Chaowang,GAO Min,FANG Dan,LU Zhicai
(Ordnance Engineering College of PLA, Shijiazhuang 050003, China)
Abstract:Trajectory correction projectiles (TCP) require to predict impact point rapidly for control system design, the truth is that it’s impossible to depict real motion of projectile with motion equation. The application of fading memory filter was proposed for impact point prediction. Based on trajectory model and impact point prediction equation, the fading memory filter-based impact point prediction equation was presented. Semi-physical simulation and flight test were carried out based on the method, the results show that the method can filter the date real-time, when the projectile trajectory is corrected, the filtered impact point prediction value will change from one state to another smoothly, it’s proved that this method can be used in impact point prediction of TCP.
Keywords:trajectory correction projectile; fading memory filter; global position system(GPS); impact point prediction(IPP)

