破碎发射药等效形状特征量的确定方法

王 燕，芮筱亭，冯宾宾，黎 超，于海龙

（南京理工大学 发射动力学研究所，南京210094）

经过多年研究，国内外对发射装药引起膛炸的机理逐步形成了共识，即相应装药结构下发射装药引起膛炸的主要原因是：弹底发射装药被点燃前受到发射装药颗粒间的挤压应力作用产生了大规模的破碎，使发射装药燃面增加，引起燃气生成速率猛增，导致弹道起始段膛压猛增而超过身管的破坏应力，产生膛炸［1］。关于破碎发射药对内弹道性能的影响，国内外进行了大量的理论研究［2］。发射药形状特征量是内弹道计算必须解决的问题。文献［3－5］在计算过程中通过改变发射药的燃速系数来表征发射药破碎；杨均匀［6］建立了破碎发射药产生的燃烧表面积与标准表面积的比值与应变、断裂模量和相对已燃质量的定量关系；张小兵等［7］通过统计破碎药粒的大小来确定破碎发射药的形状；翁春生等［8］通过增加燃气生成速率来表征发射药破碎。这些研究结果对发射安全性的研究具有一定的指导作用，但是不能准确反映真实破碎发射药。

破碎发射药由于形状大小不一，无法用几何方法直接计算发射药的形状与形状特征量等破碎发射药的物理参数，因而难以对破碎发射药进行准确的内弹道两相流动力学数值仿真。为了解决这一难题，本文基于发射装药起始动态活度比试验结果，建立了破碎发射药等效形状函数与等效形状特征量定量确定方法，用一种等效发射药的形状函数与形状特征量来表征不同形状、同一组分的多种发射药形状函数与形状特征量，其等效发射药的质量、组分和内弹道性能与不同形状的多种发射药一样。该方法为研究发射药破碎情况提供了一种定量的计算方法，解决了形状大小不一的破碎发射药在内弹道两相流动力学中准确计算的难题。

1 破碎发射药等效形状特征量计算步骤

发射药燃烧过程中燃气生成速率的变化规律与药粒的形状尺寸和燃烧速度定律相关，与前者相应的表达其规律的函数称为形状函数，后者相应的函数称为燃烧速度函数，两者综合体现了燃气生成速率随时间的变化规律。

在内弹道中，发射药形状函数为

式中：χ，λ，μ为发射药分裂前的形状特征量；χs，λs为分裂后的形状特征量；ψ为发射药已燃质量分数；Z为相对燃烧厚度；Zk为燃烧结束时的相对已燃厚度。

形状函数的本质是描述药粒的相对已燃厚度与已燃质量分数之间的函数关系，形状特征量实际上是这个函数式的系数，建立发射药形状函数过程便是利用这些系数建立发射药已燃质量分数与相对已燃厚度之间函数关系的过程。

由于形状函数是以燃气生成速率的形式来表示的，而对于同质混合装药，燃气生成速率即为各个组分燃气生成速率之和。因此，混合装药的形状函数即为不同组分装药的形状函数的线性叠加。经理论推导，将形状函数改写成ψ与e的关系：

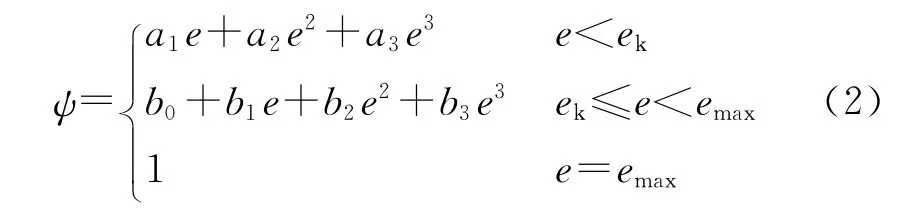
式中：多项式系数a1，a2，a3为发射药分裂前的等效形状特征量；b0，b1，b2，b3为发射药分裂后的等效形状特征量；2ek为破碎发射药分裂点处的等效弧厚；2emax为破碎发射药的最大等效弧厚。

若能获得燃烧过程中ψ－e关系曲线，便可以通过曲线拟合的方式获得发射药的等效形状特征量，从而得到等效形状函数，具体实施步骤如下。

①对破碎发射药进行密闭爆发器试验，测得p－t曲线。在装药量ω、火药力f、余容α、发射药密度ρp已知的情况下，根据密闭爆发器内气体定容状态方程：

式中：p为燃气压力，Pa；V0为密闭爆发器的容积，m3；m为发射药质量，kg；α为燃气余容，m3／kg；f为发射药火药力，J／kg。

求出发射药已燃质量分数与压力的关系，进而得到ψ－t的关系：

②根据密闭爆发器测得的p－t曲线，计算出燃烧厚度随时间的变化关系：

式中：u1为发射药的燃速系数，n为发射药的燃速指数。通过曲线积分，得到e－t曲线，令emax＝maxe。

③联立步骤①、②的计算结果，建立ψ－e的关系曲线。

④根据ψ－e曲线，采用全局连续分段最小二乘曲线拟合方法［9］确定多项式系数a1，a2，a3，b0，b1，b2，b3。将发射药等效形状特征量代入式（2）便可得到破碎发射药的等效形状函数。

2 破碎发射药等效形状特征量示例

通过发射装药动态挤压破碎试验［1］，改变活塞最大行程与点火药量，获得3组破碎程度不同的试样，如图1～图3所示。

图1 第1发低温试验破碎试样

图2 第2发低温试验破碎试样

图3 第3发低温试验破碎试样

在实际操作中，首先利用本文介绍的方法进行拟合计算，获得破碎发射药的等效形状特征量。将破碎发射药的等效形状特征量代入式（2），联立式（3）和式（5），利用数值仿真方法获得破碎发射药在密闭爆发器内燃烧的p－t曲线，进而得到相应的动态活度比曲线。如果利用破碎发射药等效形状特征量仿真得到的结果与实际试验结果相近，则认为该等效形状函数是准确的。

通过发射装药动态挤压破碎试验得到的破碎试样，运用本文建立的破碎发射药等效形状特征量确定方法，拟合计算得到的破碎发射药对应的等效形状特征量如表1所示。利用等效形状特征量仿真得到的p－t曲线与动态活度比（R）曲线如图4～图6所示，由图可见，在p／pm＜0.1时，由于受点火压力的影响，试验过程中2条曲线吻合得不是很好，但p／pm在［0.2，0.7］区间内（pm为密闭爆发器内气体压力最大值）。利用等效形状特征量仿真得到的结果与实际试验结果吻合较好。相应的起始动态活度比试验与仿真计算结果对比如表2所示，表中，E为误差，最大相对误差仅为－1.81%，说明了通过拟合计算获取破碎发射药的等效形状特征量是可行的。

表1 破碎发射药的等效形状特征量计算结果

图4 第1发破碎试样的压力－时间曲线和动态活度比曲线

图5 第2发破碎试样的压力－时间曲线和动态活度比曲线

图6 第3发破碎试样的压力－时间曲线和动态活度比曲线

表2 破碎发射药起始动态活度比R0的试验与数值仿真结果对比

3 结束语

基于发射装药起始动态活度比试验结果，利用全局连续分段最小二乘曲线拟合方法建立了一种确定破碎发射药等效形状特征量的方法。对不同破碎发射药进行了验证，表明该方法可以方便快捷地确定破碎发射药等效形状特征量，为伴随发射药破碎的内弹道两相流动力学计算提供了基础，为发射装药发射安全性研究提供了高效可靠的计算方法。

［1］芮筱亭，贠来峰，王国平，等.弹药发射安全性导论［M］.北京：国防工业出版社，2009.RUI Xiao－ting，YUN Lai－feng，WANG Guo－ping，et al.Direction to launch safety of ammunition［M］.Beijing：National Defense Industry Press，2009.（in Chinese）

［2］杨均匀，袁亚雄，张小兵.发射药破碎对火炮射击安全性影响的研究综述［J］.弹道学报，1999，11（4）：92－95.YANG Jun－yun，YUAN Ya－xiong，ZHANG Xiao－bing.Research survey of the effect of GRA in fracture on the fire safety in solid propellant gun［J］.Journal of Ballistics，1999，11（4）：92－95.（in Chinese）

［3］HORST A W，MAY I W，CLARKE E V.The missing link between pressure waves and breechblows，AD－A058 354／2GA［R］.1978.

［4］KELLER G E，HORST A W.Effects of propellant grain fracture on the interior ballistics of guns，BRL－MR－3766［R］.1989.

［5］LIEB R J，ROCCHIO J J.The effect of grain fracture on the interior ballistic performance of gun propellant［C］／／Proceedings of the 8th International Symposium on Ballistics.Orlands：IBC，1984.

［6］杨均匀.高膛压火炮发射安全性实验研究及数值模拟［D］.南京：南京理工大学，1997.YANG Jun－yun.Experimental and numerical study on launch safety in high pressure gun［D］.Nanjing：Nanjing University of Science and Technology，1997.（in Chinese）

［7］张小兵.高膛压火炮异常压力实验研究及数值模拟［D］.南京：南京理工大学，1995.ZHANG Xiao－bing.Experimental and numerical study on abnormal pressure in high pressure gun［D］.Nanjing：Nanjing U－niversity of Science and Technology，1995.（in Chinese）

［8］翁春生，金志明，袁亚雄，等.火药破碎对压力异常影响的数值模拟［J］.弹道学报，1996，8（4）：13－18.WENG Chun－sheng，JIN Zhi－ming，YUAN Ya－xiong，et al.Numerical studies on the influence of grain fracture on abnormal pressure in guns［J］.Journal of Ballistics，1996，8（4）：13－18.（in Chinese）

［9］侯超钧，曾艳姗，吴东庆，等.全局连续的分段最小二乘曲线拟合方法［J］.重庆师范大学学报，2011，28（6）：44－48.HOU Chao－jun，ZENG Yan－shan，WU Dong－qing，et al.Global continuous curve fitting method of piecewise least square fitting with global continuity［J］.Journal of Chongqing Normal University，2011，28（6）：44－48.（in Chinese）