外弹道气象诸元时空特性

陈文广，李 伟，王崇哲，李佩军，冯文占

（中国人民解放军63850部队，吉林 白城137001）

大气始终处于一种湍流运动的状态，湍流运动的基本特征是速度场在空间和时间上的分布不规则性。这种不规则性又导致了其他大气参数场（温度、湿度、压力等）分布的不规则性，结果使大气变成了一种随机非均匀介质。大量实践表明，影响火炮射击精度的因素可归结为射击诸元的计算误差和射弹散布误差［1］，其中射击诸元因素中气象条件的探测和实时误差占很大的比例，一般约占40%左右［2－4］。随着射击时间与气象通报发布时间、射击区域与气象探测取样区域距离的增大，射击开始诸元概率误差也增大。

在弹道仿真以及各种飞行器设计中，常常采用风场脉动谱定律模型［5］研究风对弹道的影响。这些模型都是在一定的假设条件下推导的，并且根据实测资料确定经验谱函数，那么这些假设与推导的使用就有局限性，并不能完全反映真实大气时空变化特点。为此本文利用青藏高原气象观测站常规实测历史资料，以及弹箭试验保障过程中连续探测气象资料，探讨了气象诸元时空变化特点的求解方法。

1 目前研究及技术规范

1.1 “冻结湍流”的假设

气象学认为时间尺度t和线性尺度r具有依存的关系，Taylor提出了对于相当小的时间间隔t，给定点的脉动速度可以无变化地随平均速度（风速）v移动，则

这就是“冻结湍流”的假设。对于中性大气状态，常见采用Dryden或Von Karman模型模拟阵风风场［6－10］，研究飞行器的飞行品质或弹道散布等。但是，实际大气是时间和空间的四维随机函数，在外弹道气象诸元表现上既可以是标量的，如温度、湿度和气压；也可以是矢量的，如风和垂直气流运动。另外，在平坦地形条件下中性大气可以近似认为水平均匀和个性同性，这种假设在射程不远，弹道高度不高，只考虑风对弹道的影响情况下，可以近似使用［11］。

1.2 气象诸元时空探测保障规范要求

在《中国人民解放军高空气象探测手册》［12］中，在中等起伏地形和气象条件稳定的情况下，规定了地炮和高炮的弹道高度H、保障半径rb和保障时效tb，如表1所示。在实施气象保障期间，一般每隔2h进行一次高空气象探测；在气象条件急剧变化或者特殊保障需要时，可增加探测和通报的次数；探测结束时间要尽量接近通报发出时间，一般在通报前1h内开始探测。

表1 炮兵气象诸元的保障能力

在气象条件相对稳定的条件下，按表1要求可以进行有效的气象保障。实际上气象诸元不仅有日变化率、年变化率，而且地域不同，变化率也不同，所以规范要求过于简单，不能充分满足弹箭科研试验气象保障的需要。

1.3 定点定时统计

关于气象诸元的实测资料的时空特性研究非常少，仅能看到某兵器试验中心的研究报告，该报告分析了水平相距54km的2个探测点位上，以时间间隔2～3h，60次高空气象同步探测的气象数据。数据以2个点位各个相同高度的气象诸元差值为样本，求得气象诸元的均方根值，然后再根据气象测控误差要求计算外弹道气象诸元气压p、温度θ、相对湿度E、风速v、风向D的保障半径rb和保障时效tb，如表2、表3所示。

表2 测控误差要求

表3 保障半径和保障时效

从表2和表3可以看出气象诸元的探测误差线性分布在固定的时间段（2～3h）、固定的水平距离（54km）内。这样，时空特性研究结果将与时间、水平距离有很强的相关性，所以其研究的科学性、普适性值得商榷。

综合以上分析可以看出，外弹道气象诸元时空特性研究大多是基于地形平坦、中性大气、射程短和弹道高度不高等假设条件，而实际上随着远程火箭弹的发展，弹道高度越来越高，射程越来越远，需要认真考虑气象诸元时空变化特性对武器系统射击精度的影响。根据我国武器发展战略以及精准火力打击的需要，我国气象保障地域已不仅限于平原地区，气象诸元时空特性研究更应关注高原与海洋。以青藏高原复杂地形的气象条件为例，如果首区和落区海拔高度相差500m，由温度垂直递减率知，海拔高度的变化引起温度变化就有3℃左右，由表3知，在弹道上仅设一个气象探测点是不能满足火炮气象诸元测控误差要求的。

2 时空特性研究

对于空间的某一固定点来说，大气参数的四维随机场可以简化为一维的随机时间函数；对于空间的某一固定时间的点来说，大气参数的四维随机场可以简化为三维的随机空间函数。本文正是基于此，通过时空分离、分段和分层等方法实现大气参数场影响因素的降维，然后再应用线性回归等方法进行时空变化规律研究。

2.1 时间特性研究

影响气象诸元变化的因素有时间、季节、经度、纬度、地形、下垫面性质以及海拔高度等。特定地点的气象诸元时间特性是一维的时间随机函数，所以时间特性研究只需考虑由时间、季节和高度变化引起的气象诸元变化。

根据研究的需要，时间可以划分到月，即某月的气象诸元的时间特性。如果需要更细的研究，可以把一天时间划分为几个时间段，在划分好的时间域内，以一定变化的时间间隔施放探空仪A，则形成施放探空仪集合：

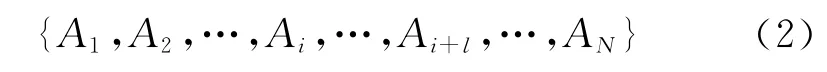
式中：i≤N，l≥1；i，l，N均为正整数，N为施放探空仪数量。

以相距一定时间间隔施放的第i和第（i＋l）2个探空仪｛Ai，Ai＋l｝作为一个子研究对象，并把探空数据按高度进行分层。在相同高度上，对2个不同时刻施放的探空仪的气象要素进行差值计算。以一定数量的高度层集合为高度层段（高度层段和弹道高度相对应），对高度层段内的差值求取标准偏差，得到标准偏差di和时间间隔ti。高度层段可以根据弹道分层高度或研究需要设定，如地面到2 000m高度段，或2 000～5 000m高度段等，而高度层段内含有许多高度层。另外，风是由风向和风速所描述的不可分割的整体，具有矢量特性，所以风速应根据风向分解成2个正交分量。分别对各个高度层上分量进行统计，在求取标准偏差后再把正交分量合成风向、风速的标准偏差。

在设定最大允许时间间隔条件下，可以得到一组某一弹道高度某一气象诸元的研究对象，把这一研究对象设定成集合：

式中：di为标准偏差，ti为时间间隔，M为在最大允许时间间隔内式（2）子研究对象的数量。

把集合（3）中对象按时间间隔由小到大的顺序进行重新排列，得到新序列集合后，以时间间隔作为直角坐标系的x轴，某一个气象诸元的标准偏差作为直角坐标系的y轴，绘出某弹道高度气象诸元标准偏差与时间间隔直角坐标关系图，根据图形可以采用最小二乘法的直线、指数、三次样条或多项式等方法对数据进行曲线拟合，并确定哪种拟合方法适合数据处理。本文根据“冻结湍流”的假设，设定气象诸元在一定时间内以微小量线性变化：

式中：a为不存在时间间隔时（t＝0），某一气象诸元由测量设备所带来的误差常量；b为以一定时间间隔施放探空仪所产生的气象诸元标准偏差随时间的变化率，是时间特性要统计的关键量。

虽然最小二乘法通过最小化误差的平方使拟合函数与原数据达到最佳匹配，但仍需在显著性水平α下应用方差检验法或相关系数检验法对回归方程进行显著性检验，判定因变量di与自变量ti之间是否存在显著的统计关系，如果回归效果显著，则存在显著的统计关系，否则不存在显著的统计关系。

在显著的统计关系情况下，已知某一气象要素弹道气象诸元测控误差要求φ和其标准偏差随时间的变化率b，则可以计算时间特性的保障时效tb：

2.2 空间特性研究

空间特性研究方法是否可以参考时间特性研究方法，调整2个探空站距离，得到以距离差为x轴，气象诸元标准偏差为y轴的直角坐标关系图，然后通过一元线性回归等方法，求得气象诸元标准偏差随距离变化的斜率。经过实测数据统计后发现，该方法无法实际描述气象诸元空间特性变化，因为某一地域某一季节气象诸元空间特性具有三维的空间特性，仅仅以一维的距离差为变量研究气象诸元的空间特性是不全面的。

地形和下垫面性质等影响因素难以量化统计，给空间特性研究带来困难。如果把我国地域划分为几个气候影响区域，例如东北地区、青藏高原地区等，就可以简化公式模型，达到参数降维的目的。有研究表明气象诸元空间特性表现为与经度、纬度和海拔高度的多元线性关系［13］，考虑应用线性模型的更一般形式即多元线性回归模型来求解气象诸元空间特性。在某月，某一区域气象诸元空间特性S与经度γ、纬度ψ、海拔高度e的关系可以表述为

式中：B0为常数项；B1，B2，B3分别为γ，ψ，e的变化系数，其单位分别由所要描述的气象诸元如温度、湿度、气压或风向、风速决定。

同样，在显著性水平α下，应用方差检验法或相关系数检验法对回归方程进行显著性检验，判定因变量S（γ，ψ，e）与自变量γ，ψ，e之间是否存在显著的线性统计关系，如果回归效果显著则存在显著的线性统计关系，否则不存在显著线性统计关系。

对回归方程的显著性检验是对回归方程中全部自变量的总体回归效果的检验，但总体回归效果显著并不说明每个自变量γ，ψ，e对因变量S（γ，ψ，e）的影响都是显著的，还需要回归系数显著性检验。如果某一自变量对因变量S（γ，ψ，e）的影响不显著，则它的回归系数就应取值为0。

在检验显著水平下，知道弹道上任意两点的经度、纬度和海拔高度差，由式（6）知，与对应的B1，B2，B3相乘后取和，就可以计算出某一外弹道气象诸元的空间特性。

3 应用分析

3.1 时间特性应用

外弹道气象诸元的时间特性算例分析是以位于青海省海拔高度4 030m某点位，于8月每天早8点至晚6点施放的近100个高空探测气球的数据为样本，2次探测最小时间间隔为40min左右，以某一探测时刻为基点，形成了一定时间间隔的子研究对象序列。设定子研究对象允许最大时间间隔（一般不要超过3h），依次向右滑动基点，则得到研究对象的集合式（3）。

以温度为例，100m厚度为一层，假设统计地面至7km高度层段探空数据，则根据式（2），每一个子研究对象｛Ai，Ai＋l｝共有70个数据，那么统计所有子研究对象，可以计算出一定时间间隔的标准偏差集合。依据式（4），绘出研究对象的标准偏差dθ、时间间隔t的关系图，如图1所示。经相关系数检验法判定dθ与t之间显著的线性统计关系后，通过最小二乘法求得温度时间特性：

式中：0.489 7℃为不存在时间差的情况下，地面至7km高空温度场由测量设备所带来的固定误差常量；0.006℃／min为温度标准偏差随时间间隔变化率。

在已知测控误差要求情况下，通过式（5）即可计算地面至7km高空温度场保障时效。需要说明的是，若探测样本的采样时间不是在8月或数据采样地点变化较大，则温度随时间变化的斜率会有所变化，其时间特性也会相应变化。

图1 气象诸元标准偏差与时间的关系

3.2 空间特性应用

外弹道气象诸元空间特性研究以青藏高原地面气象观测站和高空探测站的数据为样本。如果统计地面气象诸元的空间特性，应采用地面气象观测站数据；如果统计某一高度气象诸元空间特性，则应采用高空探测数据。

以地面和5km高度温度空间特性研究为例，把地面各个台站温度（某月平均）、经度、纬度和海拔高度带入式（6），进行多元线性回归，如表4所示，得到B0，B1，B2，B3；相关系数L，以及B1，B2，B3的检验统计量F1，F2，F3。同理，把各个探空站5km高度温度数据进行多元线性回归，得到表5。由于篇幅限制，文中不再列举气压、湿度、风向、风速等气象诸元各个高度层上的统计分析系数表。

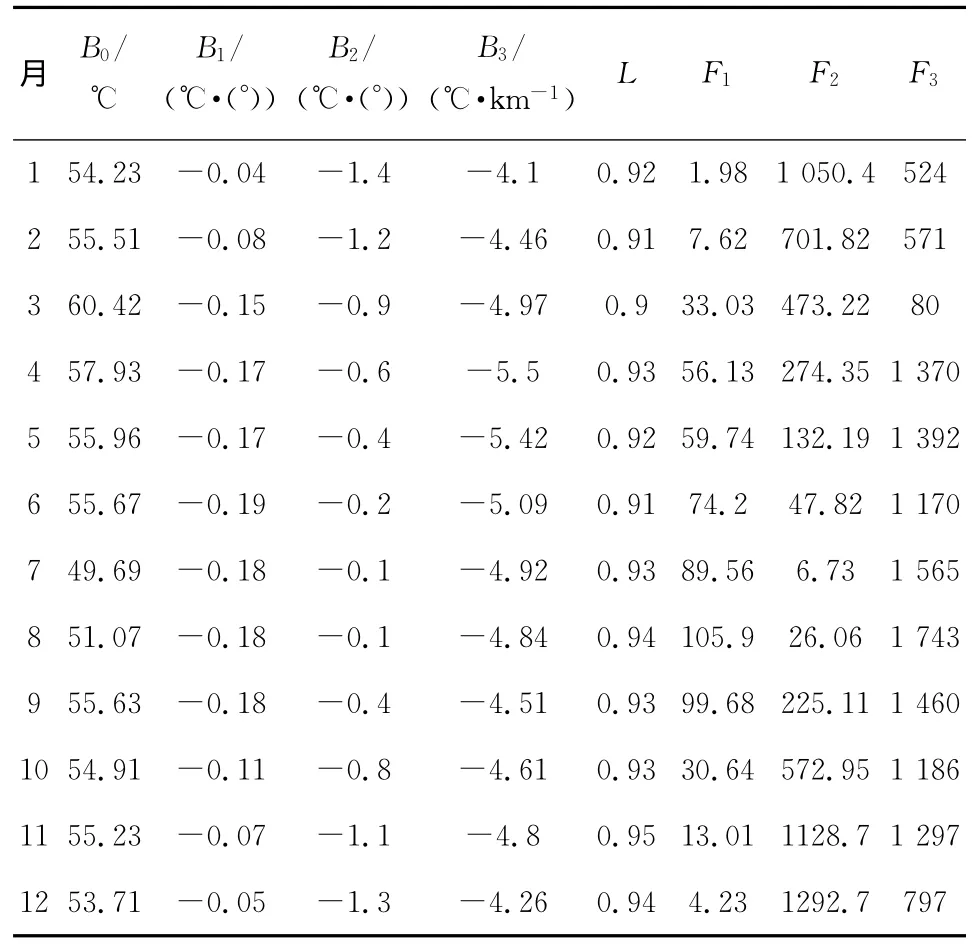
表4 地面温度空间特性统计分析系数表

从表4可以看出经度、纬度、海拔高度对青藏高原地面温度影响都为负，即随着经度、纬度、海拔高度的增加，地面温度降低；经度影响能力在1月和12月比较弱，而在6月、7月、8月和9月比较强；而纬度影响能力在冬季的1月和12月比较强，在6月、7月和8月比较弱。所以经度和纬度影响能力从时间上看正好相反。海拔高度每升高1km，地面温度大约降低5℃左右，在夏季随着海拔升高，降温明显些。从回归方程显著性检验看，相关系数都在0.9以上，回归方程具有高度显著性。从回归系数显著性检验看，经度在冬季1月、2月和12月影响效果不显著，是非主要因素；纬度在7月影响效果不显著，是非主要因素；全年中海拔高度变化是影响温度变化的主要因素。

表5 5km高度温度空间特性统计分析系数表

对比表4和表5可以看出，随着高度的增加，经度、纬度和海拔高度对温度的绝对影响能力都在减弱，海拔高度影响能力由负数变为正数；经度对温度影响变为非主要因素，而纬度在冷季仍然是影响温度变化的主要因素。

统计分析表明，青藏高原不同气象诸元的空间特性在不同季节主要影响因素不同。气压的空间特性对海拔高度和纬度变化都比较敏感，合成风速空间特性对纬度变化比较敏感，当上升到一定高度时湿度空间特性对任何影响因素都不敏感。

假设于8月在青藏高原进行远程火箭弹试验，需要计算地面层首区和落区气象诸元温度空间变化特性。设首区的地理坐标为北纬36.25°，东经94.54°，海拔高度2 808m；落区的地理坐标为北纬35.43°，东经101.45°，海拔高度2 297m；两点纬度差为－0.82°，经度差为6.91°，海拔高度差为－0.511km。把这些差值与表4对应的8月变化系数相乘取和，即可计算出首落区地面层温度空间变化为1.3℃。如果需要计算某一高度两点气象诸元的空间特性变化量，首先需要计算高空探测站某一高度的气象诸元空间特性统计分析系数表（温度、湿度、气压和风向、风速等），如表5，如已知经度、纬度和海拔高度变化量，即可计算分析这一高度气象诸元空间特性。

4 结论

本文采用时空分离，分区域、分层、分段、多元线性回归和最小二乘等数据处理方法，研究了青藏高原外弹道气象诸元时空变化特点，找出了外弹道气象诸元主要影响因素并求解了其时空变化的特性。从实际研究结果应用看，外弹道气象诸元时空特性研究方法准确可行。本文研究对弹道仿真，飞行特性研究，实际射击弹道选择，以及正确配置气象保障探测站都具有参考价值。

［1］邱瑾，牟少锋，杨军.自行火炮自动瞄准精度数据分析［J］.火力与指挥控制，2007，32（1）：105－106.QIU Jin，MOU Shao－feng，YANG Jun.Data analysis for aiming accuracy of self－propelled gun［J］.Fire Control and Command Control，2007，32（1）：105－106.（in Chinese）

［2］王兆胜.远程炮武器系统射击精度研究与射击精度战技指标论证［D］.南京：南京理工大学，2003：71－78.WANG Zhao－sheng.The study of firing accuracy and firing accuracy tactical ＆technical requirement reasoning for long range gunnery system［D］.Nanjing：Nanjing University of Science and Technology，2003：71－78.（in Chinese）

［3］杨伯忠，杨静宇.炮兵气象条件测试及其规律性研究［J］.测试技术学报，2004，18（增刊）：232－234.YANG Bo－zhong，YANG Jing－yu.Research on regularity of testing meteorological condition［J］.Journal of Test and Measurement Technology，2004，18（sup）：232－234.（in Chinese）

［4］倪庆华，曲玉琨，孙剑锋.气象条件对远程火箭炮射击精度的影响及对策［J］.指挥控制与仿真，2009，31（6）：104－107.NI Qing－hua，QU Yu－kun，SUN Jian－feng.Influence and countermeasure of meteorology condition for shooting precision of certain type of long－range rocket launcher［J］.Command Control ＆ Simulation，2009，31（6）：104－107.（in Chinese）

［5］黄华，陆汉城，徐幼平.大气扰动及其对无人机自动着陆影响仿真研究［J］.系统仿真学报，2009，21（21）：6 821－6 824.HUANG Hua，LU Han－cheng，XU You－ping.Simulation research of the atmosphere disturbance and its influence on UAVautomatic landing［J］.Journal of System Simulation，2009，21（21）：6 821－6 824.（in Chinese）

［6］徐明友.高等外弹道学［M］.北京.高等教育出版社，2003.XU Ming－you.The higher exterior ballistics［M］.Beijing：High Education Press，2003.（in Chinese）

［7］高静，洪冠新，梁灶清.Von Karman模型三维大气紊流仿真理论与方法［J］.北京航空航天大学学报，2012，38（6）：736－740.GAO Jing，HONG Guan－xin，LIANG Zao－qing.Theory and method of numerical simulaition for 3Datmospheric turbulence field based on Von Karman model computer simulation［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38（6）：736－740.（in Chinese）

［8］庞嘉斌，葛耀军，陆烨.大气边界层湍流积分尺度的分析方法［J］.同济大学学报，2002，30（5）：624－625.PANG Jia－bin，GE Yao－jun，LU Ye.Methods for analysis of turbulence integral length in atmospheric boundary－layer［J］.Journal of Tongji University，2002，30（5）：624－ 625.（in Chinese）

［9］洪冠新，肖亚伦.用蒙特卡罗法仿真生成三维空间大气紊流场［J］.航空学报，2001，22（6）：542－545.HONG Guan－xin，XIAO Ya－lun.Monte Carllo simulation for 3D－field of atmospheric turbulence［J］.Acta Aeronautica et Astronautica Sinica，2001，22（6）：542－545.（in Chinese）

［10］吴胜亮，南英，黄国强，等.随机风场与升阻比误差对空空导弹可攻击区的敏感度研究［J］.弹道学报，2012，24（2）：25－30.WU Sheng－liang，NAN Ying，HUANG Guo－qiang，et al.Attack zone sensitivity of air－to－air missile caused by random wind and error of lift－drag ratio［J］.Journal of Ballistics，2012，24（2）：25－30.（in Chinese）

［11］曲延禄.外弹道气象学概论［M］.北京.气象出版社，1987.QU Yan－lu.Introduction to the outer ballistic meteorology［M］.Beijing：Meteorological Press，1987.（in Chinese）

［12］张伟星，林国安.中国人民解放军高空气象探测手册［M］.北京：解放军出版社，2006.ZHANG Wei－xing，LIN Guo－an.The people’s liberation army high－altitude meteorological detection handbook［M］.Beijing：The PLA Press，2006.（in Chinese）

［13］李述训，吴通华.青藏高原地气温度之间的关系［J］.冰川冻土，2005，27（5）：627－632.LI Shu－xun，WU Tong－hua.The relationship between air temperature and ground temperature in the Tibetan plateau［J］.Journal of Glaciology and Geocryology，2005，27（5）：627－632.（in Chinese）