旋转伞－子弹系统动力学建模与仿真

马晓冬，郭 锐，刘荣忠，吕胜涛

（南京理工大学 智能弹药技术国防重点实验室，南京210094）

末敏子弹从母弹抛出，经过减速减旋后减速导旋主伞张开，伞－弹系统受到空气动力及系统阻尼的影响，运动一段时间后匀速下落，并绕着伞轴稳定旋转。进入稳态阶段后，伞－弹系统对地面目标进行扫描和攻击。

为了解旋转伞－末敏子弹系统稳态扫描段的运动特性，常利用高塔投放或空投的自由飞行试验方法，但系统的运动初始条件与实际工作情况相差较大。若采用炮射试验，则母弹发射时的高过载对子弹内测试系统提出很高的要求；且末敏子弹在空中运动跨度大，外部测试系统对其进行捕捉亦有难度。所以，理论建模和数值模拟研究该问题是一种更可行、更经济的手段。降落伞－载物系统是一种复杂的动力学系统，相关领域学者已提出许多动力学建模方法［1－10］。对于旋转伞－子弹系统，文献［11］将连接旋转伞与子弹的装置处理为球铰，建立伞－弹系统9自由度模型，得到弹道结果和动力学行为；文献［12］考虑末敏弹系统的连接方式、约束和伞绳弹性，建立伞、伞盘、弹3刚体系统运动的数学模型，计算结果与实测运动规律和扫描特性相符；文献［13］基于Kane方法，将旋转伞视为柔体，建立10自由度伞－弹系统刚柔两体动力学模型，得到某型末敏弹系统稳态扫描段的弹道结果。可见，已有研究中的旋转伞－子弹系统动力学模型均经过了适当的简化。

为得到更加接近实际运动的动力学模型，利用第一类Lagrange方程，建立旋转伞－末敏子弹系统的5刚体动力学模型；针对实际工况下末敏子弹弹道数据难以试验测得的问题，着重利用动力学仿真对系统动力学模型求解，通过设置边界条件得到旋转伞－末敏子弹系统稳态扫描段的弹道结果。

1 旋转伞－末敏子弹系统

旋转伞－末敏子弹系统由旋转降落伞、伞盘、摩擦盘、连杆和末敏子弹组成，如图1所示。

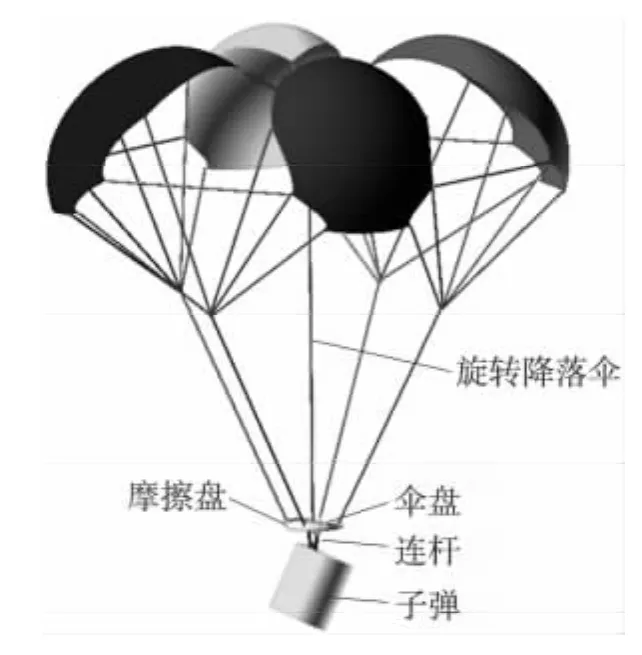
图1 旋转伞－末敏子弹系统示意图

伞衣上的开口设计使得其在下落过程中受到沿伞轴方向的空气动力矩，发生转动。伞盘和摩擦盘通过柱铰连接，中心轴线重合，扫描段初期二者相对转动，防止伞绳缠绕。摩擦盘与连杆、连杆与子弹之间各通过一个柱铰连接，柱铰的轴线与伞盘表面平行。系统经减速减旋后，旋转伞张开充满，伞盘与摩擦盘之间由于摩擦力作用，相对转动速度越来越小，连杆与伞盘、摩擦盘之间的摆动也逐渐削弱。一段时间后，伞－弹系统匀速下降，并绕铅垂轴匀速旋转，即进入稳态扫描阶段。

本文充分考虑伞－弹系统各部分之间的连接，建立5刚体动力学模型。引入以下假设：①重力加速度为常数，忽略地球的科氏加速度和曲率的影响；②不考虑伞的透气性，将其视为刚体，将伞绳视为阻尼弹簧；③不考虑伞盘、摩擦盘和连杆的空气动力，降落伞和子弹的气动参数为常数；④忽略弹体、摩擦盘等尾流对旋转伞的影响；⑤旋转伞的附加质量和附加力矩暂不考虑。

2 旋转伞－子弹系统动力学模型

2.1 坐标系

建立惯性坐标系Oxyz，O为初始时刻子弹质心的地面投影点，Oz轴沿铅垂方向且向上为正，Ox轴水平且在Oz轴与子弹中心轴组成的平面内，Oy轴由右手法则确定。

建立5个刚体的固连坐标系Oixiyizi。Oi为刚体i质心，Oizi轴沿刚体i中心轴向上，Oixi轴初始时刻与平面Oxz平行，Oiyi轴由右手法则确定，如图2所示，其中，D1，D2分别为子弹上、下表面中点，设a＝｜rO2O3｜，摩擦盘与连杆连接点在O3x3y3z3中的坐标为（0，0，－b），在O4x4y4z4中的坐标为（0，0，c），连杆与弹体连接点在O5x5y5z5中的坐标为（0，n，m）。

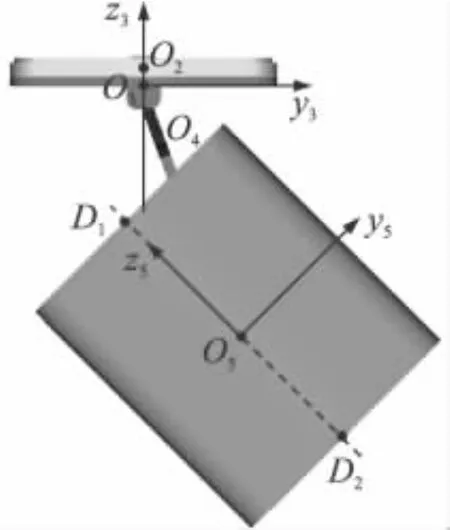
图2 部分坐标系示意图

设刚体i的欧拉角为ψi，θi，φi，则欧拉角在体坐标系Oixiyizi上的投影构成的矩阵为

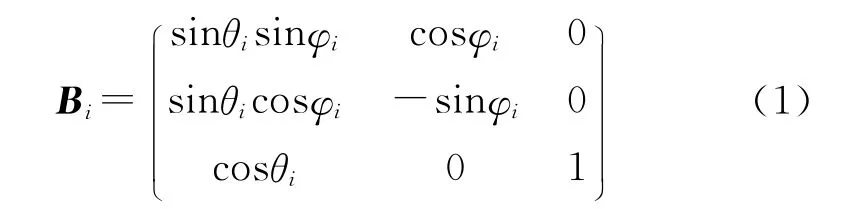
Oixiyizi到Oxyz的转换矩阵为

2.2 动力学方程

采用第一类Lagrange方程建立系统的动力学方程。用刚体i的质心笛卡尔坐标和欧拉角作为广义坐标，ri＝（xiyizi）T，pi＝（ψiθiφi）T，qi＝）T，i＝1，2，…，5。应用拉格朗日乘子法，则系统动力学方程为

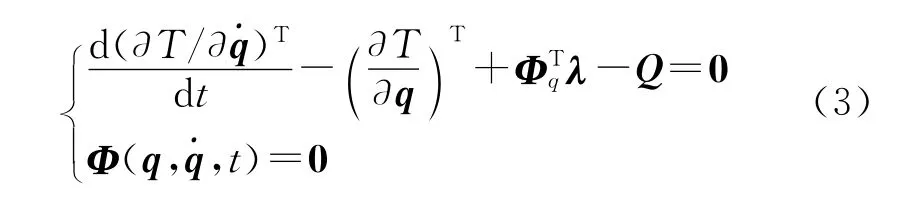
式中：T为系统动能为拉格朗日乘子阵，Q为广义力，Φq＝∂Φ／∂q。刚体i的动能为

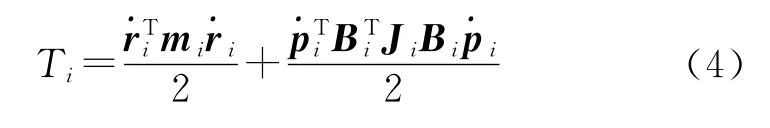
式中：mi为刚体i质量矩阵，Ji为刚体i相对质心的惯量矩阵。

经计算整理，得系统动力学方程的矩阵形式：

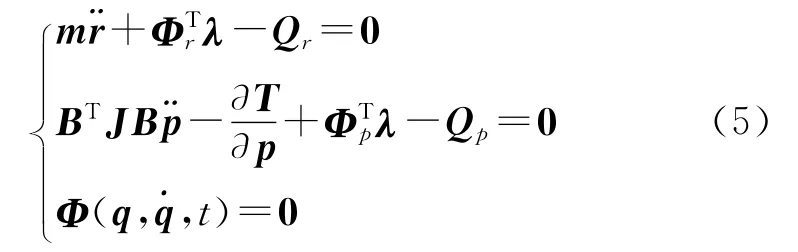
2.3 系统约束方程

旋转伞－末敏子弹系统共有3个柱铰，相邻2个刚体上给定铰点在运动过程中始终重合，如图2所示，则约束方程Φ（q，，t）＝0共15个：

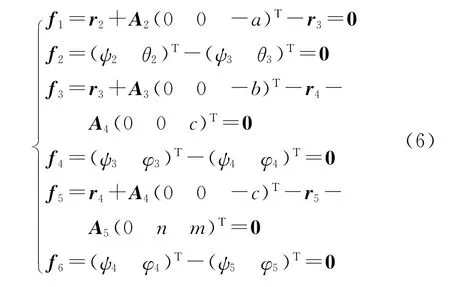
Φr均为15×15矩阵，λ＝（λ1…λ15）T。以刚体2为例，求得Φr2和Φp2：

类似地，得到Φri和Φpi，组合得到Φr和Φp。

2.4 广义力

先求各主动力在其相应虚位移上的虚功。

1）伞绳拉力虚功。

伞绳与伞和伞盘的位置关系如图3所示。伞绳矢量lj在地面坐标系中表示为［12］

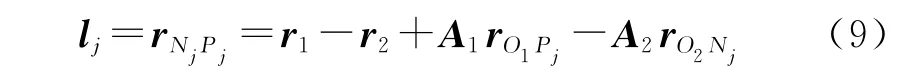
式中：Pj，Nj（j＝1，2，3，4）分别为伞和伞盘与伞绳相连接的结点，在相应体坐标系中的坐标为P1（R1，0，－h），P2（0，R1，－h），P3（－R1，0，－h），P4（0，－R1，－h），N1（R2，0，0）；N2（0，R2，0），N3（－R2，0，0），N4（0，－R2，0）；R1，R2分别为伞和伞盘的半径；h为Pj到平面O1x1y1的距离。

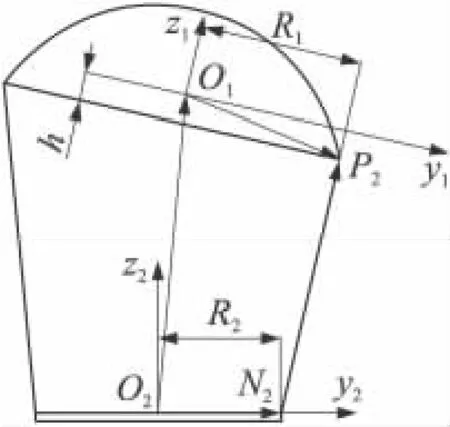
图3 伞绳与伞、伞盘的位置关系

将伞绳视为只受拉力的弹簧，原长为l0，截面积为S0，弹性模量为E，弹性系数k＝ES0／l0，阻尼系数为ν，则伞绳拉力：

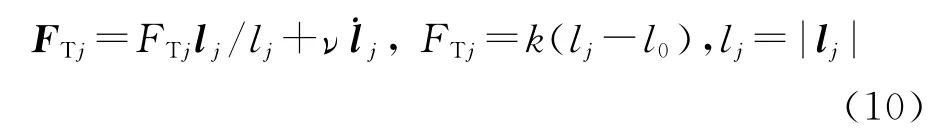
伞绳拉力所做的虚功：

2）空气动力虚功。

旋转伞所受的空气动力包括阻力FRz和升力FRy；e′1＝A1e1，为伞轴方向单位矢量在惯性坐标系的投影，则合力

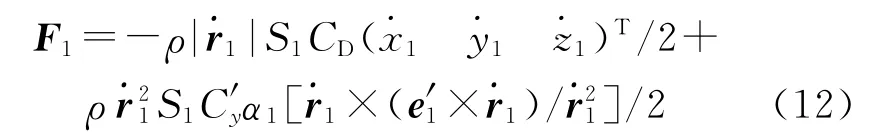
式中：CD为旋转伞阻力系数，C′y为升力系数导数，S1为旋转伞特征面积，ρ为空气密度，α1为旋转伞攻角。

旋转伞受到的空气动力矩包括导旋力矩Mxw、极阻尼力矩Mxz、赤道阻尼力矩Mzz和稳定力矩Mz，则合力矩在固连坐标系中的投影：

式中：mxw为旋转伞导旋力矩系数，m′xz为极阻尼力矩系数导数，m′zz为赤道阻尼力矩系数导数，m′z为稳定力矩系数导数，l1为特征长度，d1为特征直径。

空气动力对旋转伞做的虚功为

回来的路上，玉敏忍不住捏了捏自己的嘴。想许沁果然狡猾，自己应付不了她。自己明知姑父不可能还现金，许沁又怎么可能还自己现金呢？这种担心根本是多余的，随许沁还什么好了。玉敏暗暗佩服许沁，看来老板不是人人都做得了的。

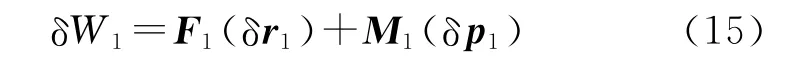
类似地，空气动力对弹体做的虚功为

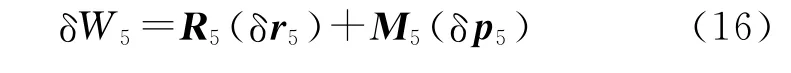
3）摩擦力虚功。

设伞盘与摩擦盘之间的作用力为FN，则摩擦力产生的力矩MN＝2μFNR2／3，摩擦力产生的虚功为

式中：μ为伞盘与摩擦盘的摩擦力系数。

4）重力虚功。

刚体i的重力Gi＝（0 0mig）T，则系统重力的虚功为

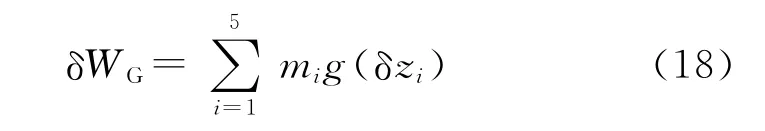
广义坐标方向上的广义力为

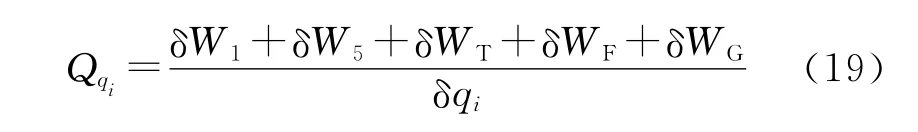
将式（11）、式（15）～式（18）代入式（19），即可得到各广义坐标方向上的广义力。

弹体扫描角为

为了与5刚体动力学模型对比，将旋转伞、伞绳和伞盘视为一体，得到4刚体动力学模型。略去伞绳拉力项，将刚体1和刚体2合并处理，按照上述步骤可得到伞－弹4刚体系统动力学方程。

3 模型试验验证

3.1 系统主要参数及初始条件

旋转伞模型采用涡环旋转伞［14］，结合流体力学软件与试验数据确定其气动力参数。经探索计算得到主要气动力参数：CD＝1.1，C′y＝0.03，mxw＝（ωb／vb）d1m′xz＝0.89（ωb和vb分别为系统的稳定转速和稳定落速），m′zz＝0.01。系统其他主要参数：m1＝0.20kg，m2＝0.29kg，m3＝0.15kg，m4＝0.02kg，m5＝12.25kg，l1＝1.2m，d1＝1.4m，k＝4.75×105N／m，ν＝0，μ＝0.3。

采用Gear预估－校正算法求解系统动力学方程，分析伞－弹系统自由下落时的弹道特性，故：t＝0时，r5＝（0 0 100）（m），pi＝0＝0，＝0。

3.2 试验验证方法

为了验证此模型模拟伞－弹系统真实运动的有效性，设计了100m高塔投放试验，如图4所示。将伞－弹系统试验模型从塔顶投下，通过姿态参数存储测量仪和高速摄像仪测试并记录其下降过程中的空中姿态参数变化规律。

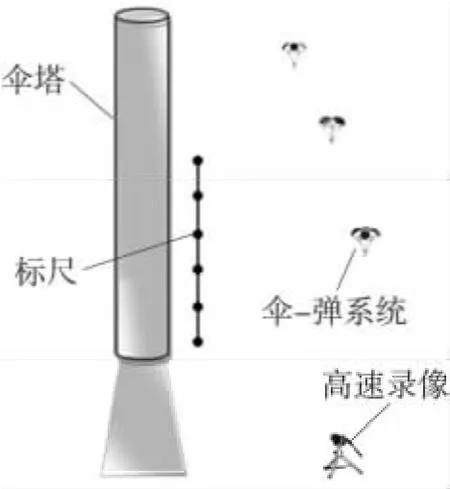
图4 正在下落的伞－弹系统

基于地磁场的近地不变性，设计一种姿态参数存储测量装置。采用三轴磁阻传感器，获得3路地磁分量并以电压U的形式输出，如图5所示，其中t′为对应的时间。试验结束回收测量仪，基于MATLAB调用存储数据进行数据处理，可以得到伞－弹系统在下降过程中的转速变化和扫描角变化。通过高速录像可得到系统通过标尺段的时间，进而推算出稳态下落段的平均速度。

图6 和图7分别为子弹转速和扫描角γ的仿真和试验结果对比。从图6可以看出：对于5刚体模型，子弹转速下落初始阶段大幅度振荡，6s开始趋于稳定，稳定转速为3.6r／s，试验得到的稳定转速在3.6r／s附近小幅变化；对于4刚体模型，没有伞绳拉力（仿真中的弹力和阻尼力）作用，子弹转速曲线十分光滑，3s达到稳定值3.6r／s。对比之下，5刚体模型更能体现旋转伞－末敏子弹系统的真实运动。从图7看出，扫描角6s开始趋于稳定值36°，伞－弹系统进入稳定状态，试验得到的扫描角约为38°，误差为5.6%。此外，仿真得到稳定落速为12.29m／s，试验得到的稳定落速为11.02m／s，误差为10.3%。导致误差的因素是动力学模型的简化、试验模型的加工误差、试验天气（如风）等。

图6 高塔试验的弹体转速变化

图7 高塔试验的子弹扫描角变化

综上所述，数值计算得到的子弹转速、扫描角变化及稳定落速与试验得到的数据吻合较好，5刚体模型能较真实地反映旋转伞－末敏子弹系统的运动。

4 算例分析

实际工作中，旋转伞－末敏子弹系统经历减速减旋后，具有一定的速度和转速。根据某末敏子弹的弹道数据设置初始条件：t＝0时，ri＝（0 0 300）（m），pi＝（0 50 0）（°）＝（36.76 120.25 －41.63）（m／s），＝（0 0 14.24）（r／s）。

计算得到的系统运动规律如图8～图11所示。

图8 实际工况的弹体转速变化

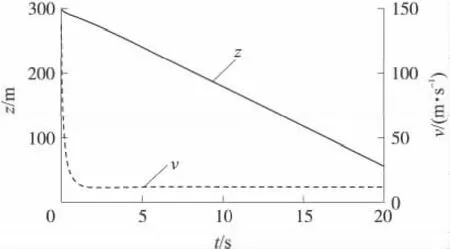
图9 实际工况的子弹高度及速度变化

图10 实际工况的扫描角变化

通过计算结果可以看出：该型末敏弹在t＝8s时速度稳定在12.29m／s，转速稳定在3.6s，扫描角稳定在36°，高度为204m；在地面上形成的扫描轨迹开始近似阿基米德螺旋线，满足末敏子弹系统稳态扫描的需要。

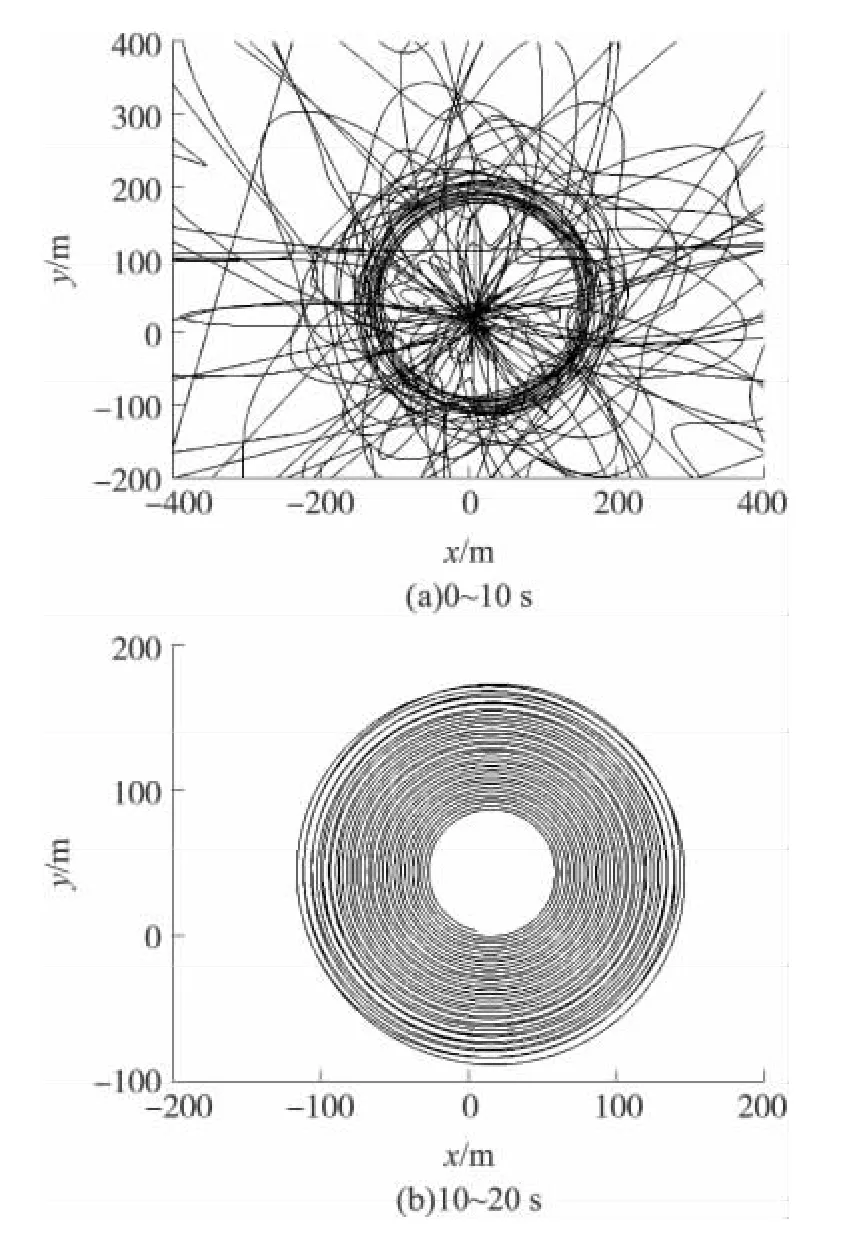
图11 0～20s地面扫描轨迹

5 结论

①模型计算结果与伞塔试验数据相符合，说明5刚体动力学模型模拟旋转伞－末敏子弹系统的运动是可行的；

②5刚体动力学模型更符合旋转伞－末敏子弹系统实际结构情况，与4刚体模型相比能更加真实地反映末敏子弹的弹道特性；

③对稳态扫描段的伞－弹系统运动进行动力学仿真计算，可得到大量的弹道结果，这是试验难以做到的，为旋转伞－末敏子弹系统的运动分析、末敏弹的总体设计以及扫描装置的设计提供了帮助。

［1］ERICKSEN R E，GUITERAS J J，LARRIVEE J A，et al.A parachute recovery system dynamic analysis［J］.Journal of Spacecraft and Rockets，1967，4（3）：321－326.

［2］WHITE F M，WOLF D F.A theory of three－dimensional parachute dynamic stability［J］.Journal of Aircraft，1968，5（1）：86－92.

［3］WOLF D F.Dynamic stability of a nonrigid parachute and payload system［J］.Journal of Aircraft，1971，8（8）：603－609.

［4］TORY C，AYRES R.Computer model of a fully－deployed parachute［J］.Journal of Aircraft，1977，14（7）：675－679.

［5］PILLASCH D W，SHEN Y C.Parachute／submunition system coupled dynamics.AIAA－84－0875［R］.1984.

［6］DOBROKHODOV V，YAKIMENKO O，JUNGE C.Six－degree－of－freedom model of a controlled circular parachute.AIAA－2002－4613［R］.2002.

［7］DOBROKHODOV V，YAKIMENKO O，JUNGE C.Simulink implementation of the 6DOF model of controlled circular parachute.AIAA－2002－4970［R］.2002.

［8］GUGLIERI G，QUAGLIOTTI F.Validation of a simulation model for a planetary entry capsule［J］.Journal of Aircraft，2003，40（1）：127－136.

［9］郑晓龙，唐硕.内装式空中发射箭伞系统多体动力学分析［J］.弹道学报，2010，22（3）：46－50.ZHENG Xiao－long，TANG Shuo.Multi－body dynamic analysis of internally carried air－launched vehicle－parachute system［J］.Journal of Ballistics，2010，22（3）：46－50.（in Chinese）

［10］周彤，冯顺山，张晓东，等.刚性伞稳定式子弹药的气动特性分析［J］.弹道学报，2013，25（4）：1－5.ZHOU Tong，FENG Shun－shan，ZHANG Xiao－dong，et al.A－nalysis on aerodynamic characteristics of rigid－parachute stabilized submunition［J］.Journal of Ballistics，2013，25（4）：1－5.（in Chinese）

［11］KARL F D，HARTMUT S.Nine－degree－of－freedom simulation of rotating parachute systems［J］.Journal of Aircraft，1992，29（5）：774－781.

［12］舒敬荣，王宝贵，韩子鹏，等.伞－弹系统三体运动分析［J］.航空学报，2001，22（6）：481－485.SHU Jing－rong，WANG Bao－gui，HAN Zi－peng，et al.Analysis on three body motion of parachute－projectile systems［J］.Acta Aeronautica et Astronautica Sinica，2001，22（6）：481－485.（in Chinese）

［13］郭锐，刘荣忠.末敏弹刚柔耦合系统动力学模型及仿真［J］.兵工学报，2007，28（1）：10－14.GUO Rui，LIU Rong－zhong.Dynamics model and simulation of rigid and flexible coupling system for terminal－sensitive submunition［J］.Acta Armamentarii，2007，28（1）：10－ 14.（in Chinese）

［14］王利荣.降落伞理论与应用［M］.北京：中国宇航出版社，1997.WANG Li－rong.The theory and application of parachute［M］.Beijing： China Astronautic Publishing House， 1997.（in Chinese）