一类分数阶q -差分系统边值问题解的存在性
孙明哲, 侯成敏
( 延边大学理学院 数学系, 吉林 延吉 133002 )
一类分数阶q -差分系统边值问题解的存在性
孙明哲, 侯成敏
( 延边大学理学院 数学系, 吉林 延吉 133002 )
研究了一类带有分数阶边值条件的分数阶q-差分系统正解的存在性.首先,给出了该问题解的表达式,并分析了格林函数的性质,然后运用基本的不动点定理证明了该问题正解的存在性和唯一性.最后,用具体例子验证了文中主要结论的正确性.
分数阶q-差分; 边值问题; 正解
q-微积分对量子力学、核及高能物理等领域的研究具有重要作用[1-2].1910年, Jackson[3]首先引入了q-微积分概念,之后Al-Salam[4]和Agarwal[5]分别给出了分数阶q-微积分的基本概念和基本性质,同时q-微积分的基本理论也得到了不断地发展[6-7].近年来,分数阶q-差分边值问题作为新的研究方向受到国内外学者的关注,而且有了一定的研究成果[8-10].文献[11]研究了非线性分数阶微分系统
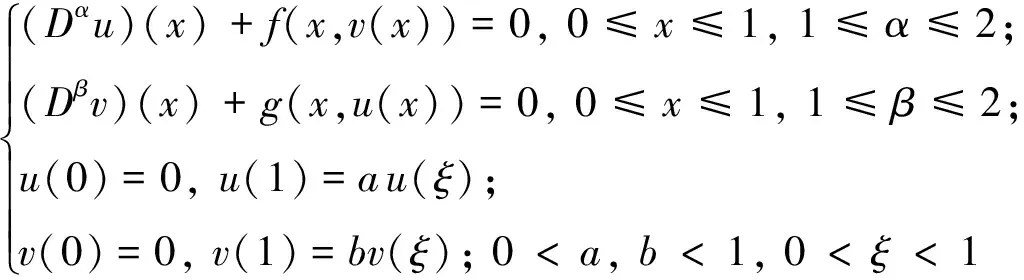
的正解.受文献[11]启发,本文讨论了非线性分数阶q-差分系统
(1)
的正解的存在性和唯一性.其中2<α, β≤3, 1<υ<2, ξ,η>0, f,g∶[0,1]×[0,+∞)→[0,+∞)为非负连续函数.
1 预备知识

定义2[8]将幂指函数(a-b)n的q-类似定义为:
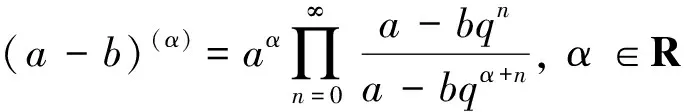
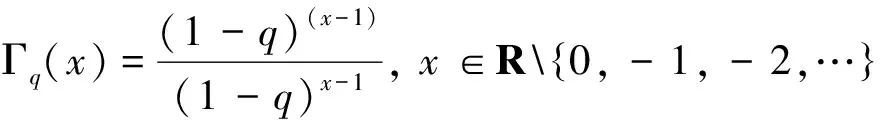
由定义3易知, Γq(x+1)=[x]qΓq(x).

定义5[8]将函数f(x)在区间[0,b]上的q-积分定义为

若函数f在区间[0,b]上的q-积分存在,则有:
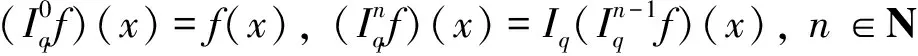
性质1[8](DqIqf)(x)=f(x), (IqDqf)(x)=f(x)-f(0) (f(x)在x=0处连续).
性质2[8][a(t-s)](α)=aα(t-s)(α),tDq(t-s)(α)=[α]q(t-s)(α-1),
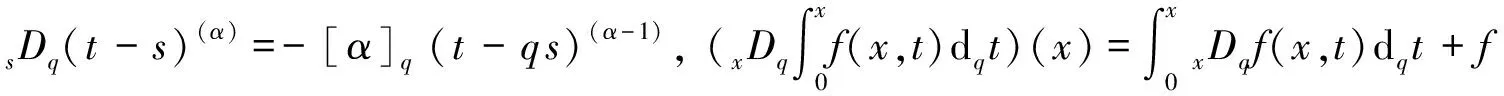
这里iDq表示与变量i有关的q-导数.
性质3[8]若α>0, a≤b≤t, 则(t-a)(α)≥(t-b)(α).
定义6[8]将Riemann-Liouville型分数阶q-积分定义为

定义7[8]将Riemann-Liouville型分数阶q-导数定义为
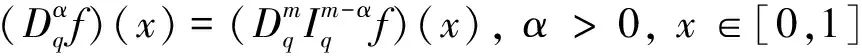
性质4[8]设α,β≥0, f(x)是定义在[0,1]上的函数,则:

性质5[8]设α>0, p是正整数,则

性质6[8]设α∈R+, λ∈(-1,∞), 则
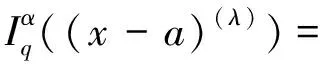
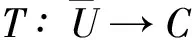
② 存在u∈∂U, λ∈(0,1)有u=λTu.
2 主要结果及其证明
考虑下面方程
(2)
定理1 设y∈C[0,1]且2≤α≤3, 那么u(t)是问题(2)的解当且仅当u(t)有以下形式:
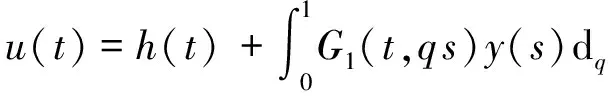
(3)

证明 假设u(t)是问题(2)的解,由定义7和性质5有

利用边值条件u(0)=0, (Dqu)(0)=0解得C3=0, C2=0.由性质4、性质6和定义7可知
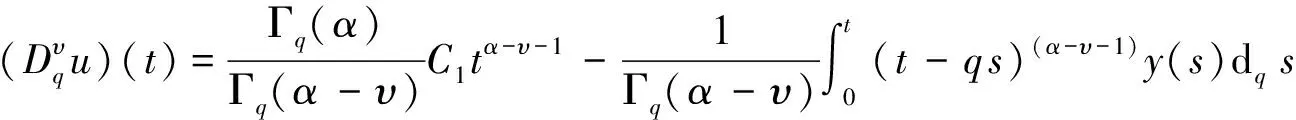
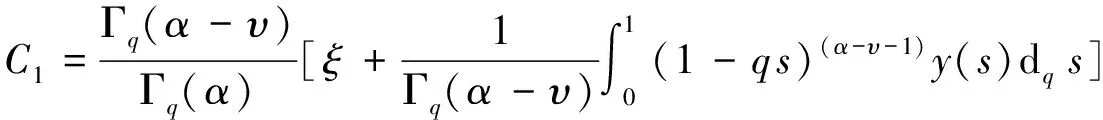
整个扇体是由多期浊流沉积而成,不同期次的浊流因规模、能量、携砂量、搬运距离、水体深度等不同,所形成的浊积扇规模、粒度、沉积厚度、沉积展布等也各不相同。因此,同一地质条件下一定范围内不同期次浊流所形成的沉积扇体,平面上呈大小不等的“串珠状”[2],剖面上呈不规则“迭瓦状”。多个“串珠”叠合即形成宏观上的大扇体(图4)。
从而

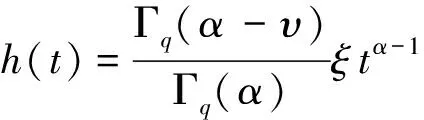
反之,如果u(t)满足(3)式,则不难推出u(t)是问题(2)的解.证毕.

定理2 格林函数G(t,s)具有下面的性质:
① G(t,s)≥0, 对一切t,s∈[0,1];
② G(t,s)≤G(1,s), 对一切t,s∈[0,1].
证明 易知G(t,s)在[0,1]×[0,1]上是连续的.下面证明G1(t,s)≥0, 记
g1(t,s)=(1-s)(α-υ-1)tα-1-(t-s)(α-1), 0≤s≤t≤1;
g2(t,s)=(1-s)(α-υ-1)tα-1, 0≤t≤s≤1.
1)易见g2(t,s)≥0.利用性质2和性质3可得
tα-1[(1-s)(α-υ-1)-(1-s)(α-1)].
同理可知G2(t,s)≥0, 即G(t,s)≥0.证毕.
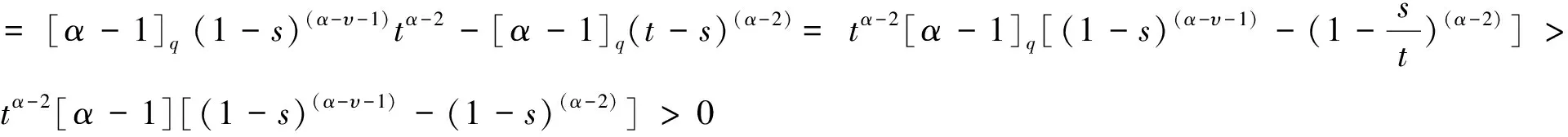
同理可知G2(t,s)≤G2(1,s), 即G(t,s)≤G(1,s)成立.证毕.
下面讨论问题(1)解的存在性和唯一性.

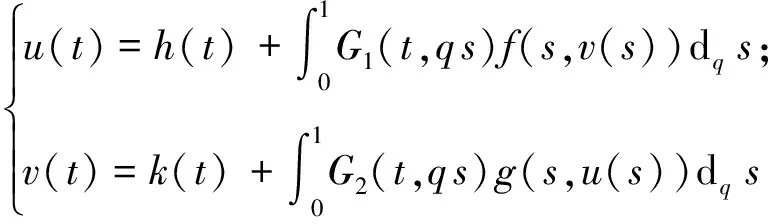
证明 由定理1易知定理3结论成立.事实上,设算子T∶X×Y→X×Y, 其中

(4)
由定理1可知,算子T的不动点即为边值问题(1)的解.
定理4 如果f(t,v), g(t,u)在[0,1]×[0,+∞)→[0,+∞)上是连续的,那么(4)式定义的算子T∶P→P是完全连续的.
证明 设(u,v)∈P, 由于G(t,q s), f(t,v), g(t,u)是非负连续函数,因此算子T∶P→P是连续的.设Ω是P的有界子集,即存在常数h>0, 对于∀(u,v)∈Ω, 有‖(u,v)‖≤h成立.选取
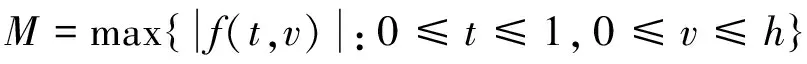
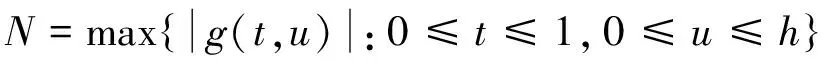
(5)
那么有


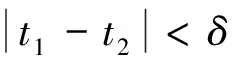
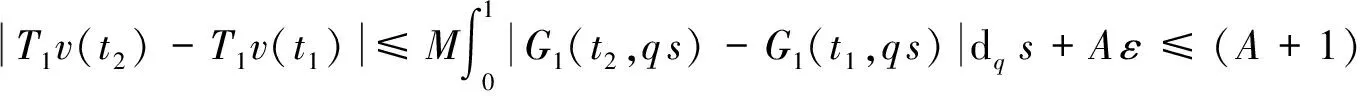
类似地,有

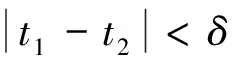

定理5 如果f(t,v), g(t,u)在[0,1]×[0,+∞)→[0,+∞)上连续,且存在函数m(t)>0, n(t)>0满足:
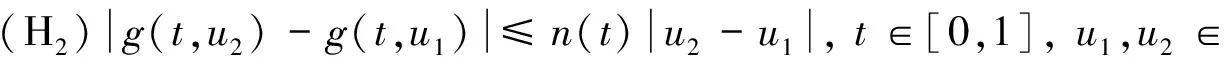
证明 设(u,v)∈P, 由于G(t,q s), f(t,v), g(t,u)是非负连续函数,有T(u,v)(t)≥0, 故T(P)⊆P.
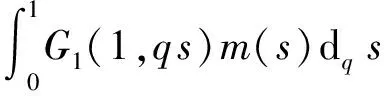
类似地,有‖T2u2-T2u1‖≤θ‖u2-u1‖.因此‖T(u2,v2)-T(u1,v1)‖≤max(ρ,θ)‖(u2,v2)-(u1,v1)‖, 即T是一个压缩映像.由定理4知T是完全连续的,由Banach不动点定理知算子T在P上有唯一的不动点,即边值问题(1)有唯一的正解.
定理6 如果f(t,v), g(t,u)在[0,1]×[0,+∞)→[0,+∞)上连续,且满足:

那么边值问题(1)至少有一个正解(u,v), 且

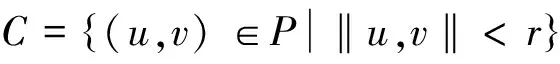

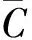
考虑特征值问题
(u,v)=λT(u,v), λ∈(0,1).
(6)
对于λ∈(0,1), 假设(u,v)是(6)式的解,则得到
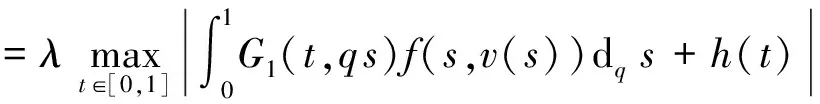
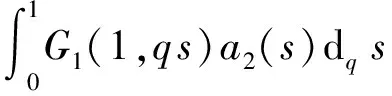
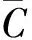
例1 考虑边值问题
(7)
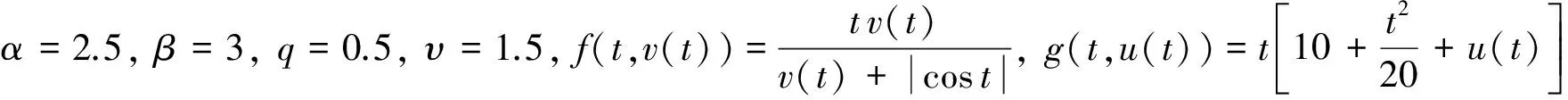
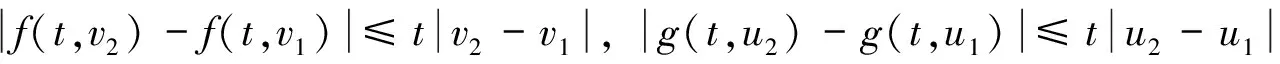

例2 考虑边值问题
(8)



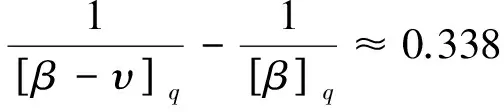

因此,问题(8)满足定理6的所有条件,从而问题(8)至少有一个正解.
[1] Strominger A. Information in black hole radiation[J]. Phys Rev Lett, 1993,71:3743-3746.
[2] Youm D. q-deformed conformal quantum mechanics[J]. Phys Rev, 2000,62(9):1-9.
[3] Jackson F H. q-difference equations Amer[J]. J Math, 1910,32:305-314.
[4] Al-Salam W A. Some fractional q-integrals and q-derivatives[J]. Proc Edinb Math Soc, 1966,17:616-621.
[5] Agarwal R P. Certain fractional q-integrals and q-derivatives[J]. Proc Cambridge Philos Soc, 1969,66:365-370.
[6] Atici F M, Eloe P W. Fractional q-calculus on a time scale[J]. J Nonlinear Math Phys, 2007,14:333-344.
[8] Rui Ferreira. Positive solutions for a class of boundary value problems with fractional q-differences[J]. Computers and Mathematics with Applications, 2011,61(2):367-373.
[9] Ahmad B. Boundary-value problems for nonlinear third-order q-difference equations[J]. Electronic Journal of Differential Equations, 2011,94:1-7.
[10] Zhou W X, Liu H Z. Existence solutions for boundary value problem of nonlinear fractional q-difference equations[J]. Advances in Difference Equations, 2013,1:1-12.
[11] Wang Jinhua, Xiang Hongjun, Liu Zhigang. Positive solution to nonzero boundary values problem for a coupled system of nonlinear fractional differential equations[J]. International Journal of Differential Equations, 2010,2010:1-13. DOI: 10.1155/2010/186928 .
Existence of solutions for boundary value problems with a coupled system of fractional q -differences
SUN Mingzhe, HOU Chengmin
(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)
We study the existence of positive solutions for a fractional q-difference system with a fractional boundary condition. Firstly, expressions of the solutions are presented, and properties of the Green function are analyzed. Secondly, the existence and uniqueness of the positive solutions of the problem are proved by basic fixed point theorem. Finally, the main conclusions are verified by some specific examples.
fractional q-differences; boundary value problem; positive solution
2014-12-15 基金项目: 吉林省教育厅“十二五”科学技术研究项目(吉教科合字[2014]第20号)
孙明哲(1979—),女,讲师,研究方向为微分方程理论.
1004-4353(2015)01-0010-07
O175.6
A

