一类具有扩散的捕食-食饵模型正解的存在性
李海侠(宝鸡文理学院数学与信息科学学院,陕西宝鸡 721013)
一类具有扩散的捕食-食饵模型正解的存在性
李海侠
(宝鸡文理学院数学与信息科学学院,陕西宝鸡 721013)
摘 要:在齐次Dirichlet边界条件下讨论了一类扩散的两食饵和一个捕食者的捕食-食饵模型正平衡态解的惟一存在性.运用隐函数定理研究了系统的二重分歧,给出了系统共存解惟一存在的充分条件.最后通过数值模拟对所得理论结果进行了验证和补充.结果表明,在一定条件下三物种能共存.
关键词:捕食-食饵模型;分歧;隐函数定理;数值模拟
0 引言
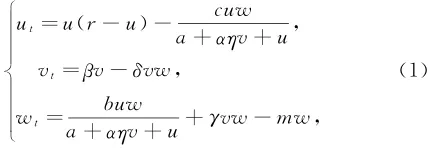
文献[1]提出了如下具有两个食饵和一个捕食者的捕食-食饵模型:其中u,v和w分别是第一个食饵、第二个食饵和捕食者的浓度.我们假设第二个食饵v是指数增长的,于是在没有捕食者的情况下第二个食饵有很大的供应量.因此,捕食者没有时间寻找第二个食饵.r代表第一个食饵u的增长率和容纳量.c和a代表了第一个食饵的最大捕食率和捕食者的半饱和常数.α=h2/h1和η=e2/e1,其中h1和h2分别表示捕食者对第一个食饵的每单位捕食量的消化时间和捕食者对第二个食饵的每单位捕食量的消化时间,e1和e2分别表示捕食者对第一个食饵的捕获率和捕食者对第二个食饵的捕获率.b代表了第一个食饵u被捕食者w消耗的转化率.β和δ分别代表第二个食饵v的增长率和捕食率.γ是第二个食饵v被捕食者w消耗的转化率.m是捕食者w的死亡率.(1)中的所有参数都是正常数.在文献[1]中,作者讨论了系统平衡点的存在性以及在这些平衡点处解的稳定性.
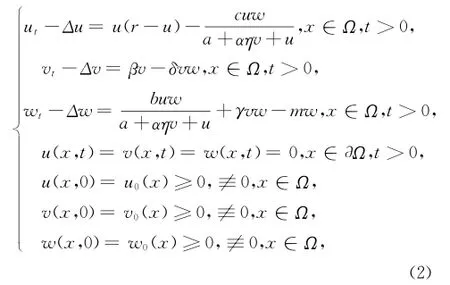
考虑到捕食者和食饵在不同空间的不均匀分布以及物种有向低浓度物种扩散的自然倾向,则系统(1)成为如下带有扩散的捕食-食饵模型:这里Ω是RN中带有光滑边界Ω的有界区域.初值u0(x),v0(x)和w0(x)都是连续函数.系统(2)是一个三物种的捕食-食饵模型.第一个食饵和捕食者之间以Holling-II反应函数相互作用,并且包含了捕食者对第二个食饵的消化时间.第二个食饵和捕食者之间以Lotka-Volterra反应函数相互作用.假设第一个食饵和第二个食饵之间没有相互作用.
目前,两物种捕食-食饵模型的研究比较多,比如文献[2-4].但三物种的捕食-食饵模型研究并不多见,尤其是具有扩散的齐次Dirichlet边界条件下的捕食-食饵模型研究甚少,如文献[5-7],其中文献[5,6]研究了三物种的捕食-食饵模型的正解的若干性质.

本文主要研究系统(2)的平衡态系统共存解的存在条件.讨论具有扩散的捕食-食饵模型共存解的存在性常见的方法有不动点指标理论和单重分歧理论.然而,寻找系统(3)共存解的先验估计具有很大的难度,因此本文采用不常见的方法空间分解法和隐函数定理来研究系统(3)共存解的存在性.
当系统(3)没有食饵时,(3)成为典型的带有Holling-II反应函数的具有扩散的两物种捕食-食饵模型.文献[8]利用不动点指数和分歧理论得到了共存解存在的充分和必要条件.文献[9,10]在齐次Neumann边界条件下也研究了此类模型.
为给出重要的结果,首先给出一些预备知识.
引理1[11]令p(x)∈C(珚Ω),λ1(p)是如下特征值问题-Δψ+p(x)ψ=λψ,x∈Ω,ψ=0,x∈Ω的主特征值,则λ1(p)连续依赖p,λ1(p)是简单的.而且,如果p1≤p2,p1p2,则λ1(p1)<λ1(p2).为了简单起见,我们定义λ1(0)为λ1,相应于λ1的主特征函数记为ψ1且‖ψ1‖2=1.


考虑如下的非线性问题如果r>λ1,则(4)有惟一正解.记惟一正解为Θr,则Θr关于r严格递增且连续可微.而且Θr≤r.因此,系统(3)当r>λ1时有弱半平凡解(Θr,0,0).
1 正解的存在性和不存在性
1.1 正解的存在性
在本小节,利用隐函数定理和空间分解讨论系统(3)的正解的存在性.我们同时以β和m为分歧参数,研究系统(3)从半平凡解(Θr,0,0)分歧出来的二重分歧.
选择p>N,令E={W2,p(Ω)∩W1,p0(Ω)}3,F={Lp(Ω)}3,其中
W1,p0(Ω)={u∈W1,p(Ω):u=0,x∈Ω}.
令珘u=u-Θr.定义映射G:E×R×R→F为其中则对所有的β和m,G(0;β,m)=0.
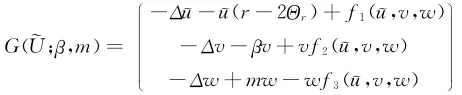
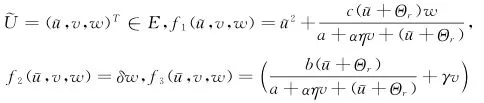
令L(β,m)是(3)在(Θr,0,0)的线性化算子,则L(β,m)=由Θ的单调性可知λ关于r是连续的
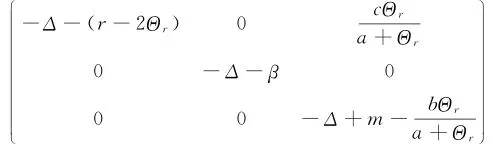
r严格递减函数.当r=λ时,当
1r→∞时,趋于λ-b.因此,如果b>1λ1,则存在r*>λ1,使得.这说明,如果-m>λ1-b,则对任意的r>r*,都存在m*使得
注:本节假设b>λ1恒成立.
简单起见,记L(λ1,m*)为L.而且,直接计算可知G珦U(0;λ1,m*)=L.不难算出L的核空间ker(L)=span{Y1,Y2},其中Y1=(0,ψ1,0)T,Y2=(φ1,0,φ1)T,这里φ1是如下问题的惟一正解:,x∈Ω,φ=0,x∈Ω 且,则dim(ker(L))=2.再令L*是L的伴随算子,则,},这里),则由Fredholm选择公理L值域为R(L)={(ω1,ω2,ω3)∈F:(ω2,ψ1)2=(ω3,φ1)2=0},则codim(R (L))=2.于是Crandall-Rabinowitz分歧定理[12]失效,因此我们用隐函数定理和空间分解的方法来研究系统(3)的正解的存在性.
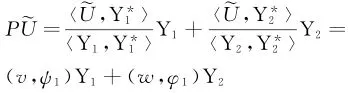
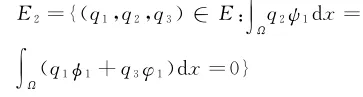
对于珦U∈F,定义投影P为分解空间E=E1+E2,这里E1=PE,且分解空间F=F1+F2,其中F1=ker(L*),F2=(I-P)F.则由投影的定义知E1=ker(L),F2=R(L).


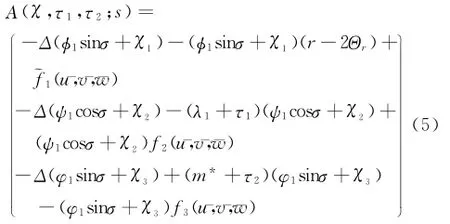
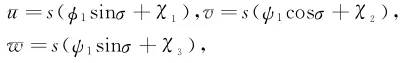
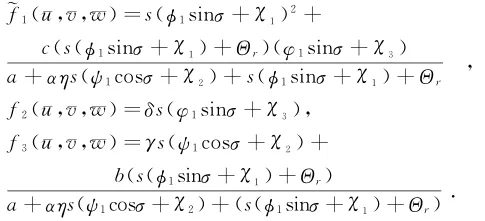
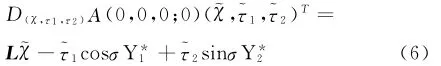
方便起见,记L1=D(χ,τ1,τ2)Α(0,0,0;0).最后,我们证明连续线性映射L1:E2×R×R→F是同构映射.设L1(χ珘,τ珓1,τ珓2)=0,因为F=F1+F2,所以和Lχ珘=0.而和是线性无关的且σ∈(0,π2),所以τ珓1=τ珓2=0.又从Lχ珘∈R(L)可知χ珘=0.因此,L1是单射.又因为F=F1+F2=ker(L*)+R(L),并且L1:E2×R×R→F,所以由(6)式和可知L1是满射,这说明连续线性映射L1是双射,即同构.因此可用隐函数定理解方程Α(χ,τ1,τ2;s)=0.也就是说,由隐函数定理可知存在一个连续可微函数(珔χ(s),珋τ1(s),珋τ2(s)),定义在s的一个小邻域内使得珔χ(0)=0,珋τ1(0)=0,珋τ2(0)=0,并且Α(珔χ(s),珋τ1(s),珋τ2(s);s)=0.设则满足珡U(s)=(珔u(s),珔v(s),珡w(s))的(珡U(s),珋β (s),珡m(s))是G(珦U;β,m)=0的解.因为φ1<0,所以由正解u的先验估计可知满足^U(s)=(珔u(s)+Θr,珔v(s),珡w(s))(ε>s>0)的(^U(s),珋β(s),珡m(s))是系统(3)的正分歧解.
上面的讨论表明了系统(3)的正分歧解的存在性.下面给出系统(3)的正分歧解惟一存在的充分条件.
定理1 若r>r*>λ1,-m>λ1-b,则(λ1,m*,Θr,0,0)是系统(3)的分歧点,而且在点(λ1,m*,Θr,0,0)的邻域内系统(3)有惟一正解.
1.2 正解的不存在性
本小节给出系统(3)正解不存在的充分条件.
定理2 如果r≤λ1或β≤λ1,那么系统(3)没有正解.
证明:假设系统(3)有正解(u,v,w),则由系统(3)的第一个方程和引理1可得这说明r>λ1,与已知r≤λ1矛盾.同理,由系统(3)的第二个方程和引理1得0=λ1(δv-β)>λ1(-β),这说明β>λ1,与已知β≤λ1矛盾.因此,如果r ≤λ1或β≤λ1,那么系统(3)没有正解.
2 数值模拟
这一节做一些数值模拟来验证和补充第一节的理论分析.在一维空间Ω=(0,l)上利用Matlab和有限差分格式来模拟系统(2),选择用二阶有限差分格式刻画空间变量,用Crank-Nicholson方法近似时间变量.取l=10,此时λ1≈0.098 7.
(1)参数c的影响.取a=5,α=0.1,η=0.5,b =2,γ=0.5,β=0.1,r=2,m=0.3,δ=0.5.从大量的数值模拟可以观察出当c增大时,u和w的浓度减少,而v的浓度增加,如图1所示.
(2)参数δ的影响.取c=2,除δ外其余参数值与(1)相同.从大量的数值模拟可以观察出δ当增大时,u和v的浓度减少,而w的浓度增加,如图2所示.
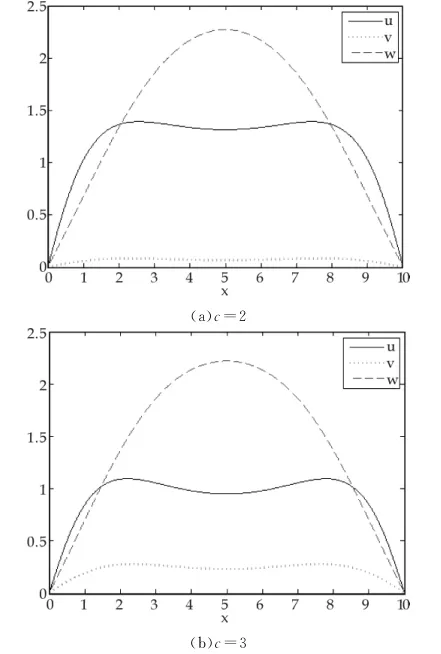
图1 参数c的影响

图2 参数δ的影响
参考文献
[1]Sharma S,Samanta G P.Dynamical behaviour of a two preys and one predator system[J].Differ Equ Dyn Syst,2014,22(2):125-145.
[2]Ko W,Ryu K.Non-constant positive steady-states of a predator-prey system in homogeneous environment[J].J Math Anal Appl,2007,327:539-549.
[3]Li Yanling,Li Haixia,Wu Jianhua.Coexistence states of the unstirred chemostat model[J].Acta Mathematica Sinica,2009,52(1):141-152.
[4]Guo Gaihui,Wu Jianhua.Multiplicity and uniqueness of positive solutions for a predator-prey model with B-D functional response[J].Nonlinear Anal,2010,72:1 632-1 646.
[5]Zhou Jun,Mu Chunlai.Positive solutions for a three-trophic food chain model with diffusion and Beddington-Deangelis functional response[J].Nonlinear Anal:Real World Appl,2011,12:902-917.
[6]Zhang Guohong,Wang Wendi,Wang Xiaoli.Coexistence states for a diffusive one-orey and two-predators model with B-D functional response[J].J Math Anal Appl, 2012,387:931-948.
[7]李海侠,李艳玲.一类带有C-M反应函数的捕食-食饵模型正解的存在性和惟一性[J].陕西师范大学学报(自然科学版),2014,42(2):7-12.
[8]Ko W,Ryu K.Qualitative analysis of a predator-prey model with Holling type-II functional response incorporating a prey refuge[J].J Differential Equations,2006,231:534-550.
[9]Yi Fengqi,Wei Junjie,Shi Jun-ping.Bifurcation and spatiotemporal patterns in a homogeneous diffusive predatorprey system[J].J Differential Equations,2009,246:1 944-1 977.
[10]Peng Rui,Shi Jun-ping.Non-existence of non-constant positive steady-state of two Holling type-II predatorprey systems:strong interaction case[J].J Differential Equations,2009,247(3):866-886.
[11]Figueiredo D G,Gossez J P.Strict monotonicity of eigenvalues and unique continuation[J].Commun Part Diff Eq,1992,17:339-346.
[12]Crandall M G,Rabinowitz P H.Bifurcation from simple eigenvalue[J].J Funct Anal,1971,8:321-340.
Existence of positive solutions for a predator-prey model with diffusion
LI Hai-xia
(Institute of Mathematics and Information Science,Baoji University of Arts and Sciences,Baoji 721013,China)
Abstract:The uniqueness and existence of positive steady-state solutions for a diffusive twopreys and one-predator predator-prey model are discussed under homogeneous Dirichlet boundary conditions.The bifurcation from a double eigenvalue for the system is investigated by virtue of the implicit function theorem and the sufficient conditions for the uniqueness and existence of coexistence states are obtained.Finally,some numerical simulations are presented to verify and complement the theoretical results.The results show that the three species will coexist under certain conditions.
Key words:predator-prey model;bifurcation;the implicit functional theorem;numerical simulations
作者简介:李海侠(1977-),女,陕西宝鸡人,讲师,博士,研究方向:偏微分方程计算及其可视化
基金项目:陕西省教育厅专项科研计划项目(14JK1035);宝鸡文理学院重点科研计划项目(ZK12042,ZK15039)
收稿日期:2015-04-05
文章编号:1000-5811(2015)04-0182-05
文献标志码:A
中图分类号:O175.26

