均匀设计法优化PVC静电纺丝工艺参数

陈思羽，吴春林，王贺云，魏忠

（石河子大学化学化工学院/新疆兵团化工绿色过程重点实验室/省部共建国家重点实验室培育基地，石河子832003）

聚氯乙烯（PVC）作为五大通用型合成树脂材料之一，在国民经济和人民生活中有广泛应用。PVC膜领域对PVC的消费量位居第三，约占10%左右[1]。传统的PVC膜及其改性膜材料大多采用压延、挤出吹塑或铸膜液浇铸流延成膜的方法制备[2]，而静电纺丝技术兴起后，人们开始研究电纺制备PVC纳米纤维膜[3]。

静电纺丝法即聚合物喷射静电拉伸纺丝法[4]。当前，静电纺丝技术已成为世界公认的能够直接连续制备聚合物纳米纤维并进一步量产的唯一方法[5]。电纺微/纳米纤维具有较大的比表面积和长径比、较高的孔隙率、优良的力学性能，且易与纳米级化学物质相结合，在催化、分离、医药等诸多领域有着潜在的应用价值[6]。溶液性质、控制变量、环境参数等因素静电纺丝法制备纳米纤维的结构和性能有很大影响[7-8]。近十年来人们从理论和实验方面探究了聚合物静电纺丝工艺特性及如何调控工艺参数控制纤维的形成过程，聚酰胺和聚乳酸等聚合物是常用的研究标本[9-13]，但极少有人系统研究PVC的静电纺丝工艺并提出一种简便的工艺优化的方法。

采用合适的试验设计方法科学安排实验，对于提高工作效率、节约科研经费及取得好的实验结果意义重大。乔江等[7]在单因素实验的基础上设计正交实验优化超疏水PVC膜的制备工艺；刘龙等[14]通过响应面分析法优化了氧化亚铁硫杆菌氧化Fe2+的条件，但对于影响因素水平众多的静电纺丝实验，均匀设计法因布点均匀、代表性好，所需实验次数大大减少，相较于其他方法更具优势。因此，本文首先通过单因素实验筛选出PVC静电纺丝的重要的工艺参数，确定各参数可取的水平范围，然后采用均匀设计法安排实验，以期用较少的实验次数得到了优化的工艺参数，为可控、有效地制备复杂的PVC纳米纤维材料奠定基础。

1 实验部分

1.1 仪器与试剂

DW-P303-1ACF0型高压电源，东文高压电源（天津）有限公司；KDS100型单通道微量注射泵，美国KD Scientific公司；JSM-6490LV型扫描电镜，日本电子公司。

SG-7型通用PVC树脂，新疆天业集团有限公司，工业级；四氢呋喃，N，N-二甲基甲酰胺，均购自天津市富宇精细化工有限公司，分析纯。

1.2 实验方法

1.2.1 PVC纳米纤维膜的制备

在室温25℃、空气相对湿度约为30%的条件下，配制一定不同浓度DMF/THF混合溶剂质量比的PVC溶液，置于回旋式气浴恒温振荡器中振荡24 h，充分溶解混合均匀后，采用一次性使用无菌注射器吸取设定容量纺丝液，夹持在KDS100型单通道微量注射泵上，安装设计型号的纺丝针，按设定的纺丝液流速和体积及给定的纺丝电压、接收装置距离，进行静电纺丝，制得一系列PVC纳米纤维膜，分别做好标记，于真空干燥箱中室温干燥24 h，用来进行扫描电镜等测试。

1.2.2 PVC纳米纤维膜的表征

（1）扫描电子显微镜分析（SEM）。将干燥待测的PVC纳米纤维膜进行真空喷金增加样品的导电性能，然后在15 kV的加速电压下表征PVC纳米纤维膜的微观形态结构。

（2）Digimizer软件图像分析。利用Digimizer软件从放大倍数为5000的SEM图像中随机抽样50根纤维进行测量，软件自动计算出样本的平均直径及标准差。

1.2.4 实验设计

大量的研究[8，15-16]表明静电纺丝除了受溶液参数（纺丝液浓度、溶剂配比）的影响外，过程参数如温度、湿度、纺丝时间、电压、纺距、纺丝液流速、纺丝针孔孔径（针头内径）等对其影响也很重要。因此，依据专业知识、以往研究结论和经验，本研究确定考察PVC纳米纤维膜成纤性状的3个主要试验指标为纤维平均直径和标准差（标准差量化反映纤维直径均匀度）、串珠数，通过单因素实验筛选对试验指标有较大影响的6个因素为纺丝液浓度和流速、静电纺电压和纺距、混合溶剂质量比DMF/THF、针头内径；再根据实验条件和以往的实践经验确定各因素的取值范围，并在此范围内设置适当的水平，为了防止最佳条件的遗漏，因素的水平适当多取一些，使试验点分布更均匀，取水平有困难时，采用拟水平法进行设计。

本实验采用均匀设计法，见表1。

1.2.5 试验结果的分析方法

由于均匀设计的试验点没有整齐可比性，所以其试验结果的分析不能像正交试验设计一样采用方差分析法，通常采用直观分析法或回归分析法。因直观分析法是从已做的有限个试验点中筛选出优化工艺条件，虽与整个试验范围内通过全面试验寻找的优化工艺条件较为逼近，但难得到精确的结果，故本研究采用Uniform design Version 3.00软件对试验结果进行回归分析，获得反映各试验因素与试验指标之间关系的回归方程，并由标准回归系数的绝对值大小判断出试验因素对试验指标影响的主次顺序，修正方程后用Microsoft Office Excel 2003软件里的规划求解宏求出回归方程在给定约束条件下的极值点，最终得出优化的工艺条件。

2 结果与讨论

2.1 单因素实验

2.1.1 纺丝液浓度对PVC电纺膜成纤性状的影响

实验结果见图1。由图1可以看出：

（1）纺丝液浓度为6%时，收集到的产品除了极细的几根纤维丝，绝大多数为电喷聚合物颗粒，说明纺丝液浓度为6%时已达可取浓度水平下限，几乎不能进行静电纺丝，成纤纤维直径可以认为是0。

（2）在其他参数固定的情况下，当纺丝液浓度从6%依次增加至16%时，成纤纤维平均直径几乎从0增加到0.82±0.20μm，而串珠数则相反，从91个减少至1个，纺丝液浓度与试验指标近似地满足线性关系。这表明纺丝液浓度对电纺纤维成纤性状有极大影响，因为在一定范围内纺丝液浓度增加，PVC分子链缠结增加，被拉伸取向的机会增加，带电射流裂分成小液滴的可能性减小，电纺膜成纤性状明显变好。

图1 纺丝液浓度对PVC电纺膜成纤性状的影响Fig.1 Effect of solution concentration on fibre traits of electrospun PVC membrane

2.1.2 DMF/THF混合溶剂质量比对PVC电纺膜成纤性状的影响

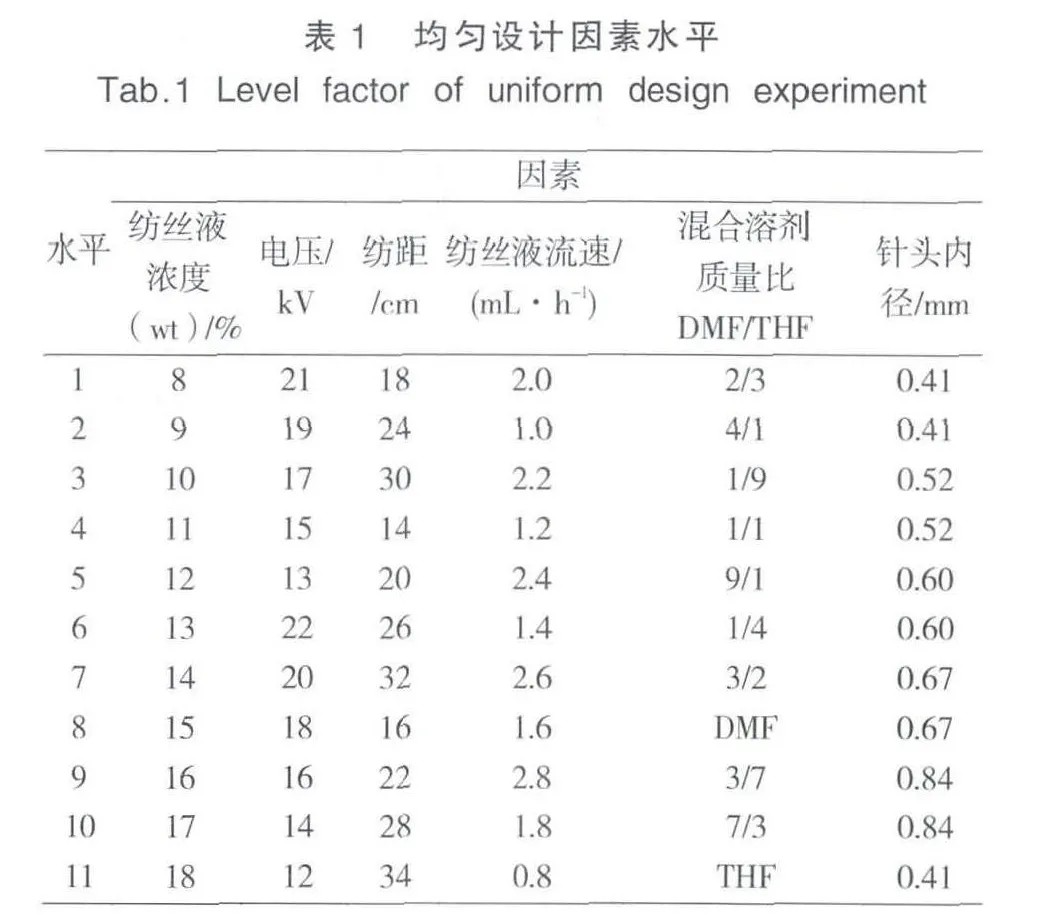
实验结果见图2。由图2可知：在其他参数固定的情况下，当DMF/THF混合溶剂质量比从1/4增加到3/2时，成纤纤维平均直径先从0.43±0.13μm增至0.89±0.29μm然后降至0.28±0.12μm，而串珠数则从11减少到1后突增至129然后平稳下降至 84。

究其原因主要为：THF是一种高挥发性、低电导率且粘度较低的溶剂，DMF则是一种不易挥发、高电导率且粘度较高的溶剂，二者单独作纺丝溶剂时都会造成电纺难以顺利进行。当二者混合作为溶剂电纺时，混合溶剂质量比对电纺成纤性状自然有极大影响。DMF/THF混合溶剂质量比为1/4时，易挥发、低电导率、低粘度组分THF含量较大，喷丝射流电荷密度较小受电场作用拉伸裂分不充分且溶剂挥发不完全，造成纤维带部分串珠；当DMF/THF混合溶剂质量比增至3/7时，射流裂分及溶剂挥发状况相应改善，电纺成纤性状较好；而进一步增大DMF/THF混合溶剂质量比时，难挥发组分DMF含量升高，射流所受电场力增加，喷丝射流拉伸裂分程度加大，成纤纤维平均直径及标准差减小，而到达接收器时间缩短溶剂挥发不完全，串珠数增多。

2.1.3 静电纺电压对PVC电纺膜成纤性状的影响

实验结果见图3。

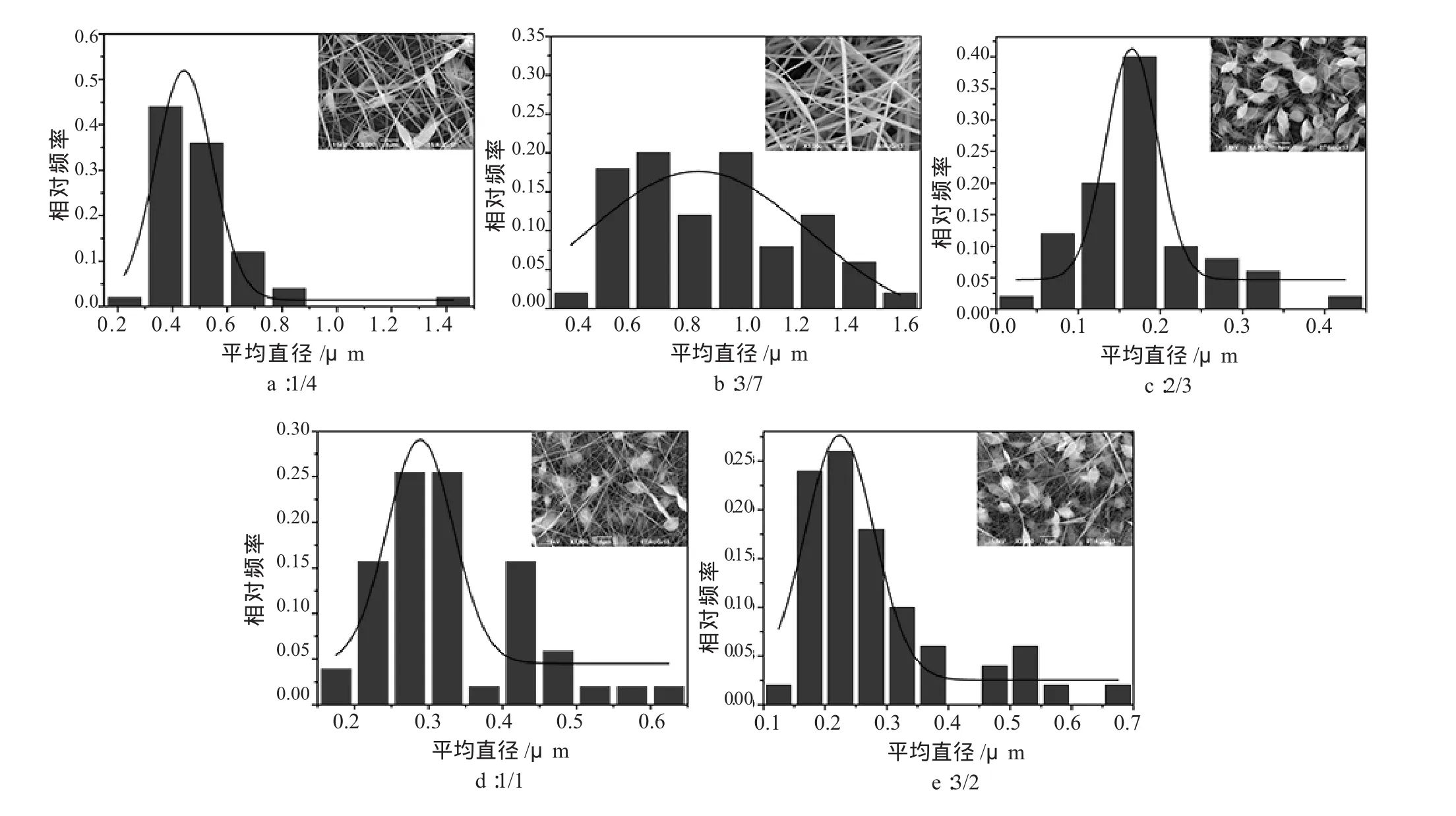
图2 DMF/THF混合溶剂质量比对PVC电纺膜成纤性状的影响Fig.2 Effect of the ratio of THF in mixture solvent on fibre traits of electrospun PVC membrane

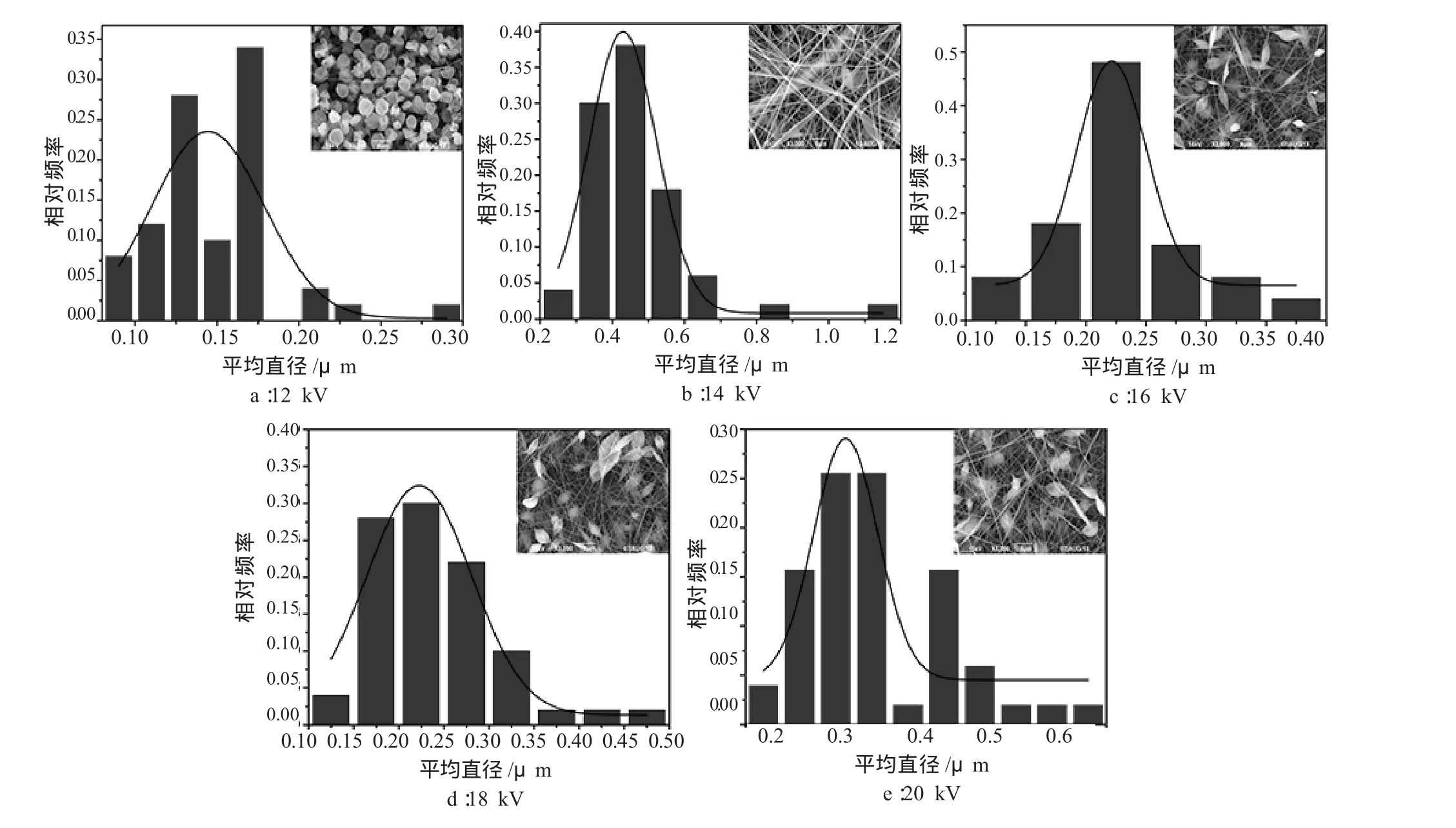
图3 静电纺电压对PVC电纺膜成纤性状的影响Fig.3 Effect of the voltage on fibre traits of electrospun PVC membrane

由图3可知：在其他参数固定的情况下，静电纺电压从12 kV依次增加到20 kV时，电纺膜纤维平均直径和标准差分别从0.14±0.035μm突增至0.47±0.1μm，但串珠数从91锐减至6后平缓增加。

这是因为其他工艺参数不变时，静电纺电压与静电场的场强成正比，一般来说，纺丝液形成的射流会随着电场强度(电压)的增加而获得更大的表面电荷密度，在电压较低时，射流受到的电场力较小，射流的裂分和拉伸受限，溶剂挥发不完全，形成较多细纤维串珠结构，当电压加大后，射流所受电场力增大，鞭动幅度增加，射流的拉伸和分化更完全，随着溶剂挥发，射流固化成纤维到达接收器，成纤性变好，但射流运动加速度变大，到达接收器时间变短，因而随着电压进一步加大，电纺膜纤维平均直径和标准差平缓下降，串珠数则逐渐增加。

2.1.4 静电纺纺距对PVC电纺膜成纤性状的影响

实验结果见图4。

从图4可以看出：在其他参数固定的情况下，当纺距从15 cm增加到 35 cm时，电纺膜纤维平均直径从（0.23±0.12）μm 逐渐增加到（0.34±0.056）μm，串珠数从16突增至80后递减至11。

造成这种现象的原因可能是纺距影响着电场强度的大小、射流鞭动运动幅度和时间及溶剂挥发的时间[7-8]，当纺距为15 cm时，电场强度较大，较大的射流鞭动运动幅度使聚合物射流在相对较短时间内充分拉伸成纤，纤维直径较小，另一方面由于溶剂挥发时间较短，成纤纤维会带少量串珠且均匀度较差。而纺距稍增大至20 cm时，射流运动及溶剂挥发时间的些许延长不足以改变电场强度锐减射流鞭动运动幅度减小所致聚合物射流拉伸不充分直径变大、串珠变多的状况；当纺距进一步增加至25 cm以上时，因受电场强度衰减幅度渐小和射流运动、溶剂挥发时间渐长的共同影响，成纤纤维直径渐大、串珠渐少。

图4 静电纺纺距对聚氯乙烯电纺膜成纤性状的影响Fig.4 Effect of the collect distance on fibre traits of electrospun PVC membrane

2.1.5 纺丝液流速对PVC电纺膜成纤性状的影响

实验结果见图5。由图5可以看出：在其他参数固定的情况下，当纺丝液流速从 0.4 mL/h增加到2.0 mL/h时，电纺膜纤维平均直径从0.23±0.04 μm 增加到 0.51±0.19μm，而串珠数则从49减至3。

这可能是因为：喷丝头端口的泰勒锥的形状会随着纺丝液流速的变化而发生一定的变化，随着纺丝液流速增加，泰勒锥变得更加稳定，使射流的不稳定性减小，可纺性变好，串珠数减少。另一方面，随着纺丝液流速增加，单位时间内可纺的聚合物的量增加，所得电纺膜纤维平均直径变大，标准差增大。

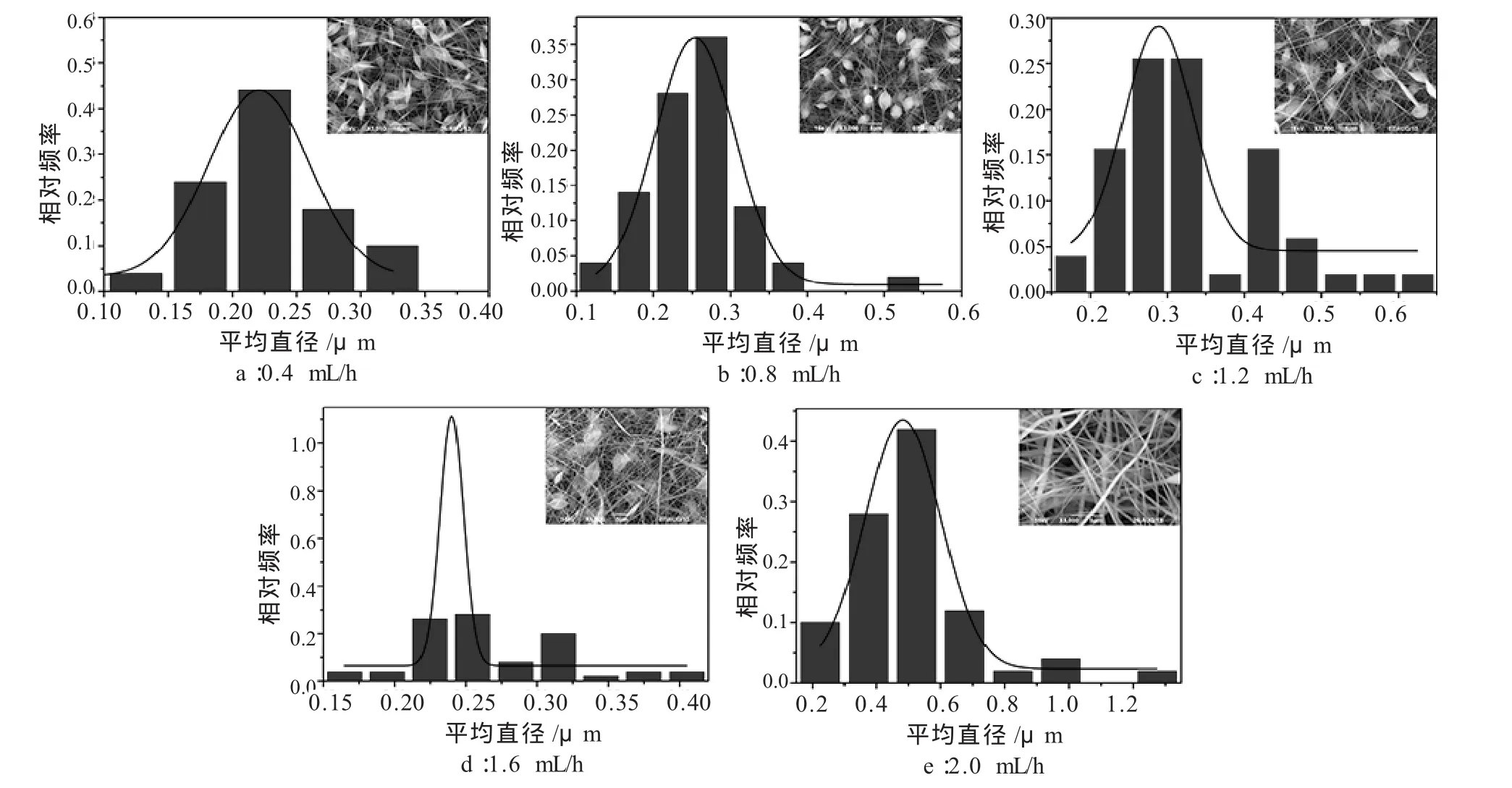
图5 纺丝液流速对PVC电纺膜成纤性状的影响Fig.5 Effect of fluid velocity on fibre traits of electrospun PVC membrane

2.1.6 针头内径对PVC电纺膜成纤性状的影响

实验结果见图6。由图6可知：在其他参数固定的情况下，仅当针头型号（本实验采用的是深圳市永泰电子工具行 18 G、19 G、20 G、21 G、22 G 五种型号的不锈钢注射针头，对应的内径分别为0.84 mm、0.67 mm、0.60 mm、0.52 mm、0.41 mm） 为 19 G时，电纺膜纤维成纤性状较好，电纺膜纤维平均直径和串珠数分别为0.42±0.20μm 和6个。其余针头型号对应电纺膜均为大量串珠和细纤维并存结构。说明针头内径对于PVC电纺膜成纤性状影响较大，且存在一个最优值。这可能是由于不同针头内径致使纺丝溶液在静电场作用力下形成泰勒锥形状不同，表面电荷密度不同，所受电场作用存在差异，造成溶剂挥发的速率、纺丝流畅性不一样，电纺膜成纤性状有差别。

图6 针头内径对PVC电纺膜成纤性状的影响Fig.6 Effect of stainless steel need les model on fibre traits of electrospun PVC membrane

2.2 均匀设计

2.2.1 均匀设计试验方案及结果

试验方案及结果如表2所示。

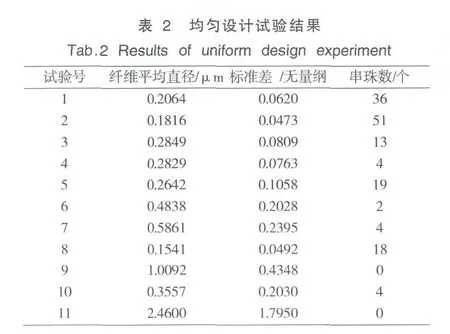
影响PVC电纺膜纤维平均直径和标准差、串珠数的因素并不是孤立发生作用，因素之间共同发生作用影响试验指标，并且由单因素实验结果分析可知各试验指标与各因素之间也并非线性关系。为了充分考察因素之间交互作用及各因素高次项对响应值的影响而又不急剧增加实验次数影响试验可行性，本实验采用均匀设计优化聚氯乙烯静电纺丝工艺。

2.2.2 回归方程的建立

（1）采用双重筛选逐步回归分析法建立纺丝液浓度（x1）和流速（x4）、混合溶剂质量比DMF/THF（x5）、针头内径（x6）、静电纺电压（x2）和纺距（x3）与纤维平均直径（y1）和标准差（标准差）（y2）、串珠数（y3）之间的回归方程。用双重筛选逐步回归分析法处理表2数据，建立3组回归方程为

（2）回归方程显著性检验。方差分析结果见表3。

注：*表示显著。

（3） 对于第 1 组方程，由于 F=822.7＞ 临界值 F(0.05，5，5)＝5.050，表明回归方程显著，相关系数R2＝0.9988，说明模型拟合度良好，实验误差较小。

对于第 2 组方程，由于 F=493.5＞ 临界值 F(0.05，5，5)＝5.050，表明回归方程显著，相关系数R2＝0.9980，说明模型拟合度良好，实验误差较小。

对于第 3 组方程，由于 F=3.367＜ 临界值 F(0.05，5，5)＝5.050，相关系数R2＝0.7711，表明回归方程总的回归效果不显著。

对于3组方程，还可以进一步进行回归系数显著性检验，因为复相关系数和F检验可以反映全部自变量的总体回归效果，但总体回归效果显著并不说明每个自变量对因变量都是重要的[17]。即可能有某个自变量xi对y并不起作用或者能被其它的xk的作用所代替，因此将这种自变量从回归方程中剔除，这样可以建立更简单的回归方程。显然某个自变量如果对y作用不显著，则它的系数β就应取值为0，因此检验每个自变量xi是否显著，就要检验假设。

（4）回归系数显著性检验。

由表4可以看出：第1组、第2组回归方程所有因素变量对各自响应值影响极其显著，回归方程为优化方程；第 3 组回归方程 x1x4、x1x5、x1x6、x52、x62对响应值的影响不显著，重新建立回归模型，得回归方程为y3=46.564-3.5818x1经显著性检验，方程回归效果显著。因此，各实验因素对试验指标的影响并非简单的线性关系。

2.2.3 规划求解回归方程的最优解

本试验为多指标的优化试验，且对各试验指标的趋势要求均是越小越好。在指定的因素数值范围内，搜索使各指标值线性加权和最小的试验条件(各指标地位的重要性通过加权系数确定)。多指标试验设计可选择一种客观赋权法对各项指标赋权。本实验选用熵值法[18]确定出各项指标的客观权重βj。由Pijln Pij可得 βj=(1-hj)，其中，当Pij=0时，规定Pijl nPij=0(Zij为标准化评价矩阵，n 为试验方案数，m 为试验指标数，i=1，2，…，n,j=1，2，…，m)，纤维平均直径和标准差、串珠数权重计算结果依次为0.2616、0.4705和0.2678。

将方程线性加权后，得到回归方程为：

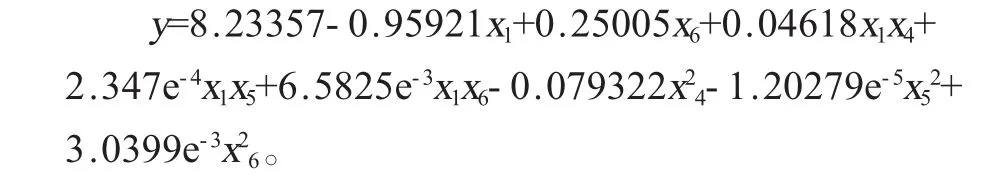
试验范围内的最优解可通过Microsoft Office Excel 2003软件里的规划求解宏求取。求出试验范围内的最佳工艺条件为：纺丝液浓度13%、流速1.2 mL/h，混合溶剂质量比DMF/THF=3/2，针头内径0.60 mm，模型给出试验指标预测值：纤维平均直径为0.2μm、标准差为0.0399、串珠数为0。

2.2.4 试验优化的验证

按上述优化条件取纺丝液浓度13%和流速1.2 mL/h、混合溶剂质量比DMF/THF=3/2、针头内径0.60 mm、静电纺电压20 kV和纺距25 cm进行试验，并对产品进行SEM表征，结果如图7所示。

图7 均匀设计优化试验结果SEM照片Fig.7 The SEM of the optimized test result leaded by uniform design

由图7可知：纤维平均直径和串珠数分别为（0.225±0.0528）μm和0个，与回归方程预测值接近，并且优化条件与对均匀设计试验结果的直观分析结果及单因素最优原则筛选结果相近，说明该模型预测性和可靠性很好。

3 结论

（1）通过均匀设计，基于相对较少的试验范围内实验点数据分析构建出了关于纤维平均直径和标准差、串珠数的回归方程为：

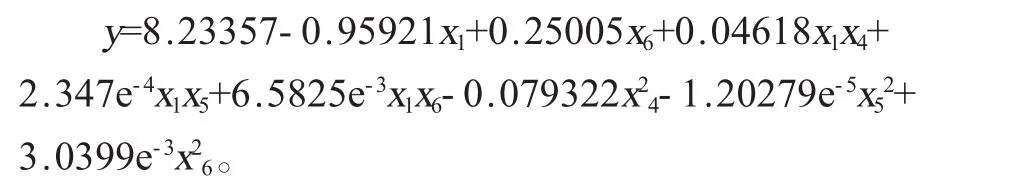
（2）确定了聚氯乙烯静电纺丝最佳工艺参数为：纺丝液浓度13%、流速1.2 mL/h、混合溶剂质量比DMF/THF=3/2、针头内径0.60 mm、静电纺电压20 kV和纺距25 cm。

（3）通过回归方程对最佳工艺条件下纤维平均直径和标准差、串珠数预测，结果表明：预测值与实验值（纤维平均直径和标准差、串珠数分别为0.225 μm、0.0528、0）接近。这表明均匀设计是一种简便可靠的多因素多水平实验优化方法，优化后的PVC静电纺丝工艺参数能为可控、有效制备复杂的聚氯乙烯纳米纤维材料奠定基础。

[1] 高以烜，赵玉琴，吕秀开，等.聚氯乙烯(PVC)超滤膜及工业化[J].北京工业大学学报，1992，18(2)：80-87.GAO Yixuan，ZHAO Yuqing，LV Xiukai，et al.Polyvinyl Chloride(PVC)Ultrafiltration Membrane and Its Industrial Production[J].Journal of Beijing Polytechnic University，1992，18(2)：80-87.

[2] Wang C J，Gong C Q，Peng T Y，et al.High photocatalytic degradation activity of the polyvinyl chloride（PVC)-vitamin C(VC)-TiO2 nano-composite film[J].Journal of Hazardous materials，2010，178：152-156.

[3] Zhu X S，Jiang X S，Cheng S，et al.Preparation of high strength ultrafine polyvinyl chloride fibrous membrane and its adsorption of cationic dye[J].Journal of polymer research，2010，17：769-777.

[4] 赵敏，潘福奎.静电纺丝法浅析[J].山东纺织科技，2010，51(6)：47-50.ZHAO Min，PAN Fukui.Introduction of Electrospinning[J].Shandong Textile Science&Technology，2010，51(6)：47-50.

[5] Huang Z M，Zhang Y Z，Kotaki M，et al.A review on polymer nanofibers by electrospinning and their applications in nanocomposites[J].Composites science and technology，2003，63(15)：2223-2253.

[6] Rutledge G C，Fridrikh S V.Formation of fibers by electrospinning[J].Advanced drug delivery reviews，2007，59(14)：1384-1391.

[7] Shin Y M，Hohman M M，Brenner M P，et al.Electrospinning：A whipping fluid jet generates submicron polymer fibers[J].Applied Physics Letters，2001，78(8)：1149-1151.

[8] Agarwal S，Greiner A，Wendorff J H.Functional materials by electrospinning of polymers[J].Progress in Polymer Science，2013，38(6)：963-991.

[9] Deitzel J M，Kleinmeyer J，Harris D E A，et al.The effect of processing variables on the morphology of electrospun nanofibers and textiles[J].Polymer，2001，42(1)：261-272.

[10]Theron S A，Zussman E，Yarin A L.Experimental investigation of the governing parameters in the electrospinning of polymer solutions[J].Polymer，2004，45(6)：2017-2030.

[11]A H Hekmati，A Rashidi，R Ghazisaeidi，et al.Effect of needle length，electrospinning distance，and solution concentration on morphological properties of polyamide-6 electrospun nanowebs[J].Textile Research Journal，2013，0(00)：1-15.

[12] 乔江，王兵，蒋亚楠，等.静电纺丝法制备超疏水聚氯乙烯膜工艺研究[J].石河子大学学报：自然科学版，2011，29(2)：244-247.Qiao Jiang，Wang Bing，Jiang Yanan，et al.Preparation Process of Super-hydrophobic PVC Membrane by Electrospinning[J].Journal of Shihezi University：Natural Science 2011，29(2)：244-247.

[13]Cui W，Li X，Zhou S，et al.Investigation on process parameters of electrospinning system through orthogonal experimental design[J].Journal of applied polymer science，2007，103(5)：3105-3112.

[14] 刘龙，孙艳芳，郭志国，等.响应面分析法优化氧化亚铁硫杆菌氧化 Fe2+的条件 [J].石河子大学学报：自然科学版，2014，32(6)：750-754.LIU Long，SUN Yanfang，GUO Zhiguo，et al.Optimization of Fe2+Oxidation by T.ferrooxidans Using Response Surface Method[J].Journal of Shihezi University：Natural Science 2014，32(6)：750-754.

[15]林金友.静电纺微纳米多级结构纤维制备及其在油水分离中的应用[D].上海：东华大学，2012：36-66.

[16]王朋.纳米结构硅材料的制备及其在锂离子电池中的应用研究[D].兰州：兰州大学，2013：3-4.

[17] 方开泰.均匀设计及其应用[J].数理统计与管理，1994，13(1)：57-63.FANG Kaitai.The uniform design and its application[J].Application of Statistics and Management，1994，13(1)：57-63.

[18] 魏效玲，赵立新，任建华.多指标试验设计综合加权评分值的确定[J].河北建筑科技学院学报，2003，20(4)：68-72.WEI Xiaoling，ZHAO Lixin，REN Jianhua.Determine on synthetically weighted mar value of multiple attribute test[J].Journal of Hebei Institute of Architectural Science and Technology，2003，20(4)：68-72.