基于ANSYS/LS-DYNA的铁路货车缺陷轴承振动特性研究

朱爱华，朱成九

ZHU Ai-hua1 , ZHU Cheng-jiu2

（1.华东交通大学 机电工程学院，南昌 330013；2.华东交通大学 土木工程学院，南昌 330013）

0 引言

20世纪60年代以来，我国就已经开展对滚动轴承振动和噪声的研究[1～4]。刘寿祥等通过对LM11949/10、NU211等轴承零件作单因素交叉试验和对国外同型号产品振动对比分析，找出了圆锥滚子轴承各零件对轴承振动的影响规律，得出滚子波纹度是影响轴承振动加速度和振动速度高频档的主要因素[5]。夏新涛等以实验为基础，运用数理统计分析的方法研究了轴承振动与噪声的关系[6]。1982年，邓聚龙创立灰色系统理论，以小样本、贫信息不确定性系统作为研究对象，从已知信息中提取有价值的信息，达到对系统行为和规律的预测和控制[7,8]。刘劲军、夏新涛和张立红利用灰色系统理论研究影响圆锥滚子轴承振动的影响因素，得出滚子凸度和滚子直径偏差等参数对滚子轴承振动影响最大[9]。本文在其基础上，利用ANSYS/LS-DYNA显式动力学，建立轴承主要元件如内、外圈及滚子的点缺陷模型进行动力学仿真分析，研究轴承主要元件有点缺陷时对振动的影响及振动特征，找出判断依据。

1 点缺陷及轴承有限元模型

滚子轴承会因疲劳、裂纹、压痕、胶合等失效形式引起滚动体和内、外圈表面剥落,这是滚动轴承常见的故障。表面剥落所形成的点缺陷恶化会导致整个轴承的故障甚至报废[10]。

内、外圈和滚子的点缺陷模型是在正常轴承353130B模型[11～16]的基础上通过引人“人工点缺陷”建立的。在内、外圈和滚子承载区分别构造1个凹坑，点缺陷半径约1mm，深度为2mm，形状为球冠[17～19]，如图1所示。

轴承材料均为硬度较大的钢材，塑性变形相对弹性变形几乎可忽略不计，因此假设轴承材料为各向同性的线弹性材料，密度为7800kg/m3，弹性模量为210GPa，泊松比为0.3。实际工况中，外圈固定在轴承基座上，因此将外圈全部约束，约束施加在外圈外表面节点上，由于所选单元SOLID164没有旋转自由度，只有平移自由度，所以只需约束x、y和z方向的平动即可。轴承的载荷通过转轴作用在内圈上，因此将转速加载在内圈内表面刚体上，径向荷载施加在内表面刚体的轴线上。

材料参数和边界条件均采用正常模型的参数，内、外圈和滚子点缺陷模型及网格划分如图1所示。在ANSYS/LS-DYNA显式动力学中，分析轴承各元件分别有点缺陷时对轴承振动的影响，通过计算得到，正常轴承、滚子点缺陷轴承、内圈点缺陷轴承和外圈点缺陷轴承的内圈滚道节点Y方向加速度变化曲线。

2 振动信号的时域分析方法

振动信号是轴承故障诊断中应用最普遍的检测信号，运用合适的信号处理方法提取所检测到的振动信号，就能识别轴承的故障所在。因此信号处理方法的选择就显得尤为重要。目前信号处理方法主要有：时域分析和频域分析。时域分析是最简单的振动监测方法，它反映的是轴承总体运行情况，它能判断出轴承是否发生故障。本文主要采用时域分析对振动信号进行仿真分析，得到各元件有点缺陷时轴承振动的时域判断指标如下。

2.1 有量纲统计参数

对于离散时间序列x1,x2,x3,…,xn，振动的各有量纲统计参数计算如下：

1）峰值xp：振动信号的最大值。

3）均方根值xrms：用来判断轴承是否正常运行。

4）方根幅值xr：反映振动信号波动程度。

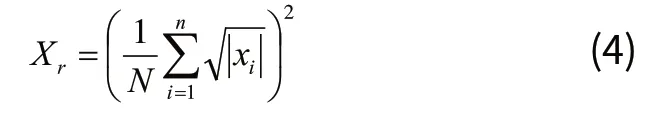
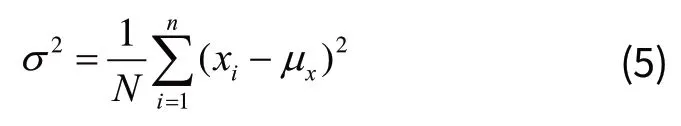
6）方差均值比Q：反映振动信号的集散程度。

2.2 无量纲统计参数

1）波形指标Sf：反映振动信号的波动程度。

2）峭度指标K：反映振动信号的冲击特征。

3）脉冲指标If：反映振动波形冲击分量的偏离程度。

4）峰值指标Cf：检测是否存在冲击的指标。

5）裕度指标Ce：检测是否存在冲击的指标。

3 加速度时程分析

为了分析轴承在不同状态下加速度的变化规律，选取初始状态时，正上方内圈滚道中心点，提取其Y方向的加速度变化曲线来进行分析。图2～图5分别为正常轴承、滚子点缺陷轴承、内圈点缺陷轴承和外圈点缺陷轴承的内圈滚道节点Y方向加速度变化曲线。

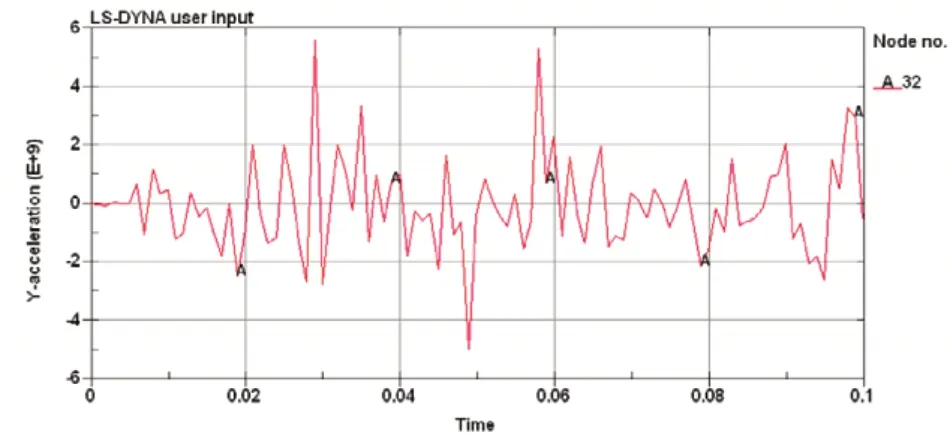
图2 正常滚子轴承内圈节点Y方向加速度曲线

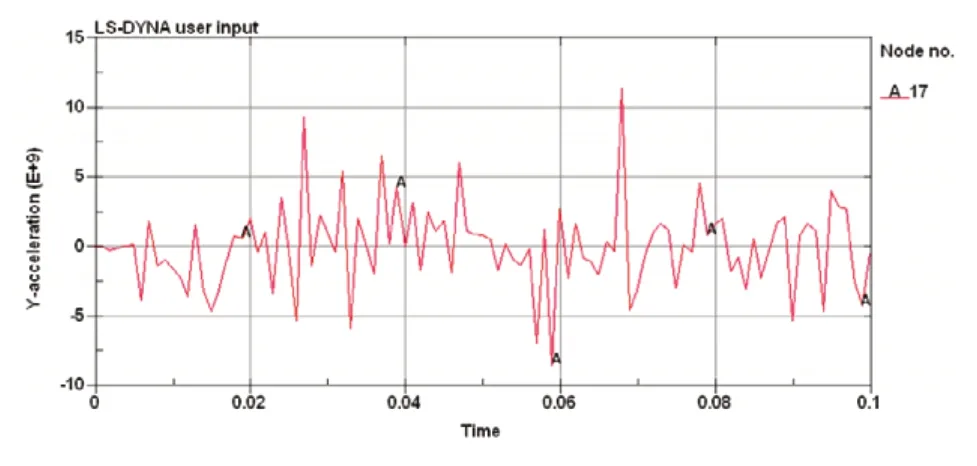
图3 滚子点缺陷轴承内圈节点Y方向加速度曲线

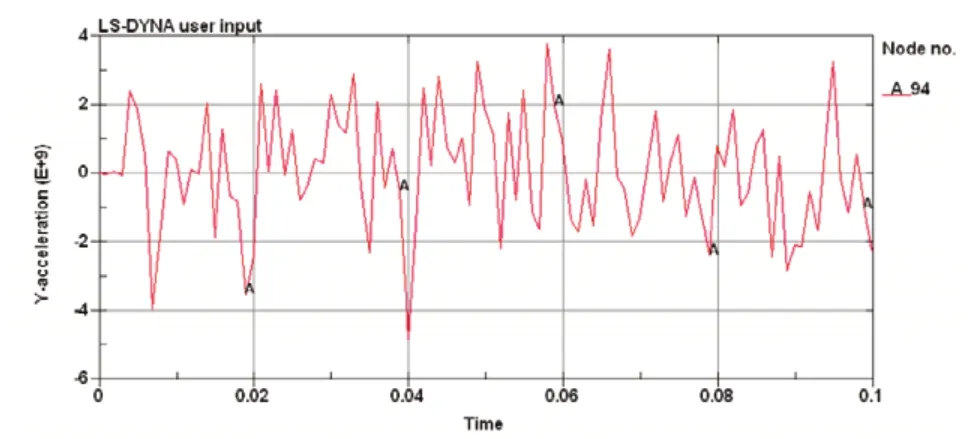
图4 内圈点缺陷轴承内圈节点Y方向加速度曲线

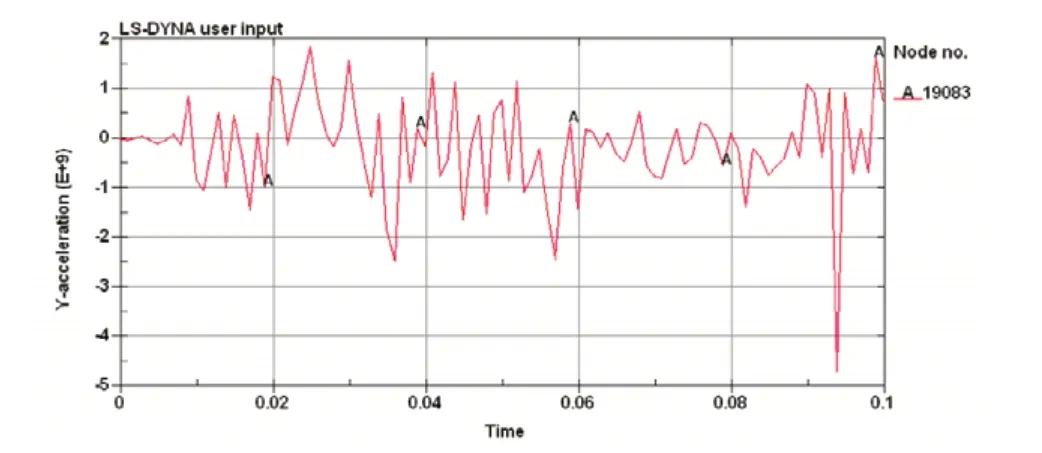
图5 外圈点缺陷轴承内圈节点Y方向加速度曲线

从图2～图5可以看出，正常情况下轴承与有点缺陷情况轴承相比较，内圈滚道节点Y方向的加速度曲线没有明显的规律可循，不同时刻的峰值大小也不一样，呈现高度的随机性，这反映了轴承元件运动及受力的复杂程度。为研究各元件有点缺陷时对轴承运动的影响，利用振动的时域统计参数对加速度曲线进行进一步分析，结果如表1所示。

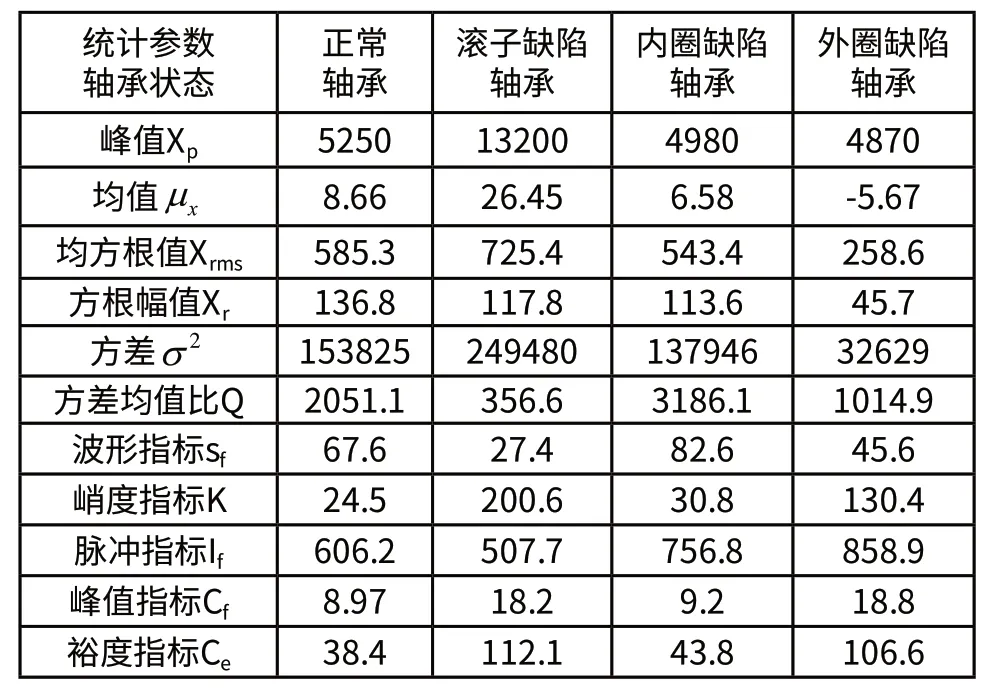
表1 轴承振动时域统计参数值（单位：106mm/s2）

4 轴承振动统计参数分析

4.1 振动有量纲统计参数分析

由表1可得，当轴承滚子出现点缺陷时，峰值、均值和方差均明显变大，均方根值虽然变大，但幅度不是太大，方差均值比和方根幅值都有减小，且方差均值比减小的幅度更明显，但当外圈出现点缺陷时，方差均值比也明显减小，所以不能单一使用方差均值比作为滚子点缺陷的判断指标，因此可以用峰值、均值和方差来作为轴承滚子点缺陷的判断指标；当内圈出现点缺陷时，峰值、均值、均方根值、方根幅值和方差都小幅度减小，但减小的幅度不是很明显，而方差均值比成明显的增长趋势，因此可用方差均值比作为内圈点缺陷的判断指标；当轴承外圈出现点缺陷时，振动的峰值和均值小幅度减小，均方根值、方根幅值、方差和方差均值比明显减小，因此均方根值、方根幅值和方差可以用作外圈点缺陷出现的判断指标。

4.2 振动无量纲统计参数分析

由表1可得，当轴承滚子出现点缺陷时，波形指标和脉冲指标都有减小趋势，且波形指标减小的幅度更明显，峭度指标、峰值指标和裕度指标有明显的增大趋势；当内圈出现点缺陷时，峭度指标、峰值指标和裕度指标都没有明显的变化，而波形指标和脉冲指标有所增加；当外圈出现点缺陷时，除了波形指标有减小的趋势外，其他参数都成明显的增长趋势，由此可以得出，对于轴承元件点缺陷的出现，不能用单一的无量纲统计参数来判断，但可以综合无量纲统计参数的变化情况来判断轴承元件点缺陷的出现。当峭度指标、峰值指标和裕度指标明显增加，但脉冲指标却呈减小趋势时，可以判断此时可能在轴承滚子上出现了点缺陷；当波形指标减小，但其他参数却都明显增大时，这时可能在轴承外圈上出现了点缺陷；当轴承内圈点缺陷时，其无量纲统计参数没有明显的变化，因此不适合用无量纲统计参数来判断轴承内圈是否发生点缺陷。

5 结论

铁路货车轮对使用的3531310B型滚动轴承结构复杂，本文基于ANSYS/LS-DYNA显式动力学，建立3531310B型滚动轴承内、外圈及滚子的点缺陷模型，进行动力学仿真分析，通过提取正常轴承和有点缺陷轴承运行时内圈滚道节点Y方向的加速度曲线，进行轴承振动信号时域分析，通过分析和比较振动信号的时域统计参数可得到如下结论：

1）内圈滚道节点Y方向加速度曲线没有明显的周期性，呈现随机性，反映了轴承运动时内部元件受力的高度非线性。

2）当滚子出现点缺陷时，峰值、均值和方差较其他元件有点缺陷变化明显，因此可以用峰值、均值和方差作为滚子点缺陷的判断指标。

3）当内圈出现点缺陷时，方差均值比与其他元件有点缺陷相比有明显的变化，因此可以用方差均值比来作为内圈点缺陷的判断指标。

4）当外圈点蚀出现时，均方根值、方根幅值和方差较其他元件有点缺陷明显减小，因此可以用均方根值、方根幅值和方差来作为外圈点缺陷的判断依据。

5）单一的无量纲统计参数无法正确地对轴承缺陷进行判断，但将无量纲统计参数进行综合比较分析，可以作为点缺陷的判断依据，如当峭度指标、峰值指标和裕度指标明显增加，但脉冲指标却呈减小趋势时，可以作为滚子点缺陷判断的依据；当波形指标减小，但其他参数却都明显增大时，可以作为外圈点缺陷判断的依据；轴承内圈点缺陷因其无量纲统计参数没有明显的变化，不适合用无量纲统计参数来判断轴承内圈是否发生点缺陷。

[1]尚梅.铁路轴承接触疲劳性能的研究[J].材料工程,1996,14(6):24-25.

[2]范文明,邓立,孟庆江.铁路货车滚动轴承故障对行车安全的影响及防范[J].铁道技术监督,2004,31(4):35-36.

[3]李学军,姚百惠.故障滚动轴承的转子系统基座振动响应特性分析[J].轴承,2011.

[4]Tallian LD,Gustafsson.Progress in rolling vibration research and control[J].ASLE Trans,1965,8(3):195-207.

[5]刘寿祥,沈国祥,吕亚芳.降低圆锥滚子轴承振动噪音[J].轴承,1999.

[6]商锦海.圆锥滚子轴承振动值分析[J].轴承,2000.

[7]姜利平.降低滚子轴承振动值及噪声的措施[J].轴承,2004.

[8]夏新涛,马伟,颉潭成,等.滚动轴承制造工艺学[M].北京:机械工业出版社,2007.

[9]姜利平.降低圆锥滚子轴承、短圆柱滚子轴承振动值及噪声[J].轴承技术,2003.

[10]张根源,周泓,常宗瑜.存在点缺陷的深沟球轴承的动力学响应[J].浙江大学学报(工学版),2009,43(8):1497-1450.

[11]小林政弘,桥本正义.滚动轴承的噪声和振动问题(2)[J].机械的研究,1968,20(2):316-320.

[12]Oswald B.Noise and Vibrational behaviour of rolling bearing,ball and roller engineering[J].Industrial Engineering (FAG),28:4-11.

[13]Tandon N,Choudhury A.A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J].Tribology International,1999,555532:469-480.

[14]夏新涛,谭成,孙立明,等.滚动轴承噪声理论与实践[M].北京:机械工业出版社,2005.

[15]夏新涛.滚动轴承磨削谐波控制理论及应用[M].北京:兵器工业出版社,2000.

[16]夏新涛,王中宇,孙立明,等.滚动轴承振动与噪声关系的灰色研究[J].航空动力学报,2004,19(3):424-428.

[17]徐勇.基于LS-DYNA研究铁路货车缺陷轴承振动特性[D].南昌:华东交通大学,2014.

[18]张乐乐,谭南林,樊莉.滚动轴承故障的显式动力学仿真与分析[J].上海交通大学学报,2007(09):1506-1509.

[19]张志伟,韩振南,王志坚.基于ANSYS/LS-DYNA的圆柱滚子轴承的动力学特性研究与故障模拟[J].煤矿机械,2013,34(08):309-311.